河口海岸水沙动力环境多尺度时空耦合数值模拟研究进展

王芳宇，陈汨梨,，张启博，谢守鹏，张继生*

(1.河海大学 港口海岸与近海工程学院，南京 210024；2.中国港湾工程有限责任公司，北京 100027)

河口海岸是陆海相互作用的集中地带，各种物理过程耦合多变，演变机制复杂，生态环境敏感脆弱。同时，该地带经济较为发达、人口集居，日益增多的人类活动会加剧河口海岸地区环境压力。因此，河口海岸的研究、开发和保护是当前世界沿海国家和科学家关注的热点问题。

学者们通常采用物理模型试验、数值模拟和现场观测等手段开展河口海岸水沙动力环境的多尺度时空耦合作用研究。随着计算机科学技术的快速发展，数值模拟凭借成本低、速度快、预测性强、结果可视化等优势成为当前河口海岸水沙动力环境研究的重要手段，并在工程实践中得到广泛应用。因此，本文总结了波浪、潮流、泥沙同一物理场的多尺度时空耦合及不同物理场间的单一时空耦合模拟研究进展，为今后河口海岸水沙动力环境数值模拟提供研究思路及方向。

1 同一物理场多尺度空间耦合模拟研究

随着河口海岸资源的持续开发与环境保护地不断推进，实现小规模沿海水沙动力的准确预测愈发重要。当使用大范围水沙动力方法模拟大陆坡及小规模近海动力环境时，由于大小范围网格间的空间尺度差异，在描述垂向网格变化时较为困难[1]。近年来，填海工程造成的区域泥沙运动特征的改变以及对港口、航道和海岸生态系统的影响也愈来愈受到广泛的关注，并且泥沙淤积带来的问题尤其复杂。虽然目前同一物理场大范围模拟的方法相对成熟，能准确刻画大范围水沙动力特性，但在局部水沙特性的刻画上仍不够精细。因此，如何考虑同一物理场不同空间尺度的相互作用，已成为准确模拟河口海岸水沙动力特性的关注重点。

1.1 单向嵌套

近年来，学者们发现虽计算流体力学方法能求解完整的Navier-Stokes方程，捕捉不同尺度的水流流动现象。但是小尺度模拟对计算资源需求过大，仍不适用于工程实践。另外，由于空间小尺度现象和大尺度现象间的相互影响不可忽视，迫切需要同步实现大范围水动力场的预测及局部动力场的精确模拟。

基于此，学者开始着眼于同一物理场的多尺度空间嵌套模拟，以大范围模型的模拟结果作为边界条件驱动小范围模型。吴文挺等[2]通过嵌套模拟的方法搭建了高分辨率的模型网格，将临近海域的海岸动力过程降尺度传递到小尺度河口地区。随后Möhring等[3]发展了流体动力平面定位系统的多尺度建模方式，基于有限元软件Ansys，使用Flotran求解器实现模型嵌套，证明了嵌套模型相较于简化模型的优越性。Nash和Hartnett[4]利用MSN_Flood平台开发了多尺度嵌套模型，该模型在精度和计算量间取得良好平衡且在复杂嵌套边界上有独特的处理方法(如图1)。图2展示了Nash等采用四级联嵌套网格(90 m、30 m、6 m和2 m四个不同空间尺度)对较粗网格PG数据进行空间内插，以填充下一级较细子网格CG边界数组(P为父网格，C为子网格)。嵌入PG90中的第一层子网格CG30以3:1(△x_P/△x_C)的嵌套比在重点区域缩小，在5:1的嵌套比下CG30为CG06提供东部边界条件，最高分辨率的CG02则以3:1嵌套比嵌入CG06中[5]。由于小尺度水流常存在复杂边界及源、汇项等问题，且模型精度受差分网格几何形态限制[6]，因此在实现多尺度空间水流过程的高效模拟方面仍有欠缺[7]。

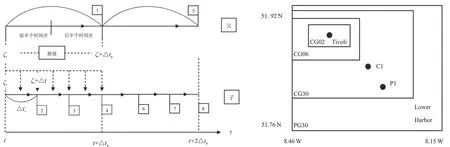
图1 嵌套过程示意图

泥沙数学模型作为研究和解决近海水域泥沙冲淤问题的有效工具已得到较为普遍的运用[8]。一维模型计算省时但无法给出各物理量的平面范围分布，虽二维模型能较准确模拟但计算量较大经济性欠缺[9]。兼顾一、二维模型的优缺点，Zhang[10]应用一、二维嵌套技术，将河海连接处视为节点，由此成功地模拟了黄河口的演变。李玉婷等[11]考虑河口悬沙运动冲淤的变化，采用大小尺度双重嵌套的方法建立了河口海岸泥沙二维模型，高峰等[12]在分析鸭绿江河口实测水文泥沙资料的基础上，采用MIKE21 FM模块建立了基于多重嵌套网格模式的泥沙场数学模型，验证表明该嵌套模型能较好地反映泥沙的运动特征，可以为今后开展进一步的相关工程规划和设计提供有效工具。张修忠等[13]也建立了一种河口海岸一、二维嵌套的泥沙数学模型，通过交界面实现数据在每一迭代步进行耦合计算，能用较少的机时复演、预测重点部分的细部变形情况，验证结果表明在河口海岸处建立的一、二维嵌套泥沙数学模型是一种解决某些实际工程问题的可靠和高效的工具。

1.2 双向耦合

跨空间尺度完成小范围与大范围网格之间的数据交互，准确模拟多尺度空间耦合现象，对研究各物理场的本质至关重要。因此，为更精细刻画小尺度复杂水流过程，实现不同空间尺度下各流场信息的双向互馈，曾季才等[14]建立多尺度空间数值离散的三维水流运动耦合模型，用以获取全区域大尺度解及多子域小尺度高精度解。该模型采用了三维Darcy水头插值算法[15]及尺度分离策略，在获取区域大尺度粗网格解的同时精细刻画局部小尺度水流运动过程。将不同尺度模型的空间信息关联传递，以实现多尺度空间耦合模拟。相比传统局部嵌套模型，该模型能更精确刻画局部尺度的复杂水流运动过程。

在大规模沿海水流运动模拟中，Agnieszka等[16]首次提出POM-MSN_Flood建模耦合系统，并将其用于研究复杂潮汐引起的河口海岸水动力。验证结果表明该模型能有效解决与水流特征尺度相对应的流体运动，包括东北大西洋的大规模流动和沿海水域精细环流。Zhang等[17]在建立近岸波流耦合的非结构化四叉树网格数值模型时，以树状数据结构实现网格连通性和数据传递性。Wu等[18]为准确模拟小范围沿海水流的水动力特性，将局部计算流体力学模型[19]与大范围非结构化网格海洋模型耦合，前者用于捕获小尺度流，后者用于预测大尺度流。在局部模型中将小尺度流场划分为相互重叠的双向耦合子域，基于Schwartz交替迭代[20]和研发的质量守恒算法[21]，实现子域间解的衔接过渡。如图3所示，大范围非结构化网格海洋模型采用内外模式求解离散化流动，将局部模型与大范围模型的三维内模式相耦合，在网格交界面上交换速度分量，完成数据交互。

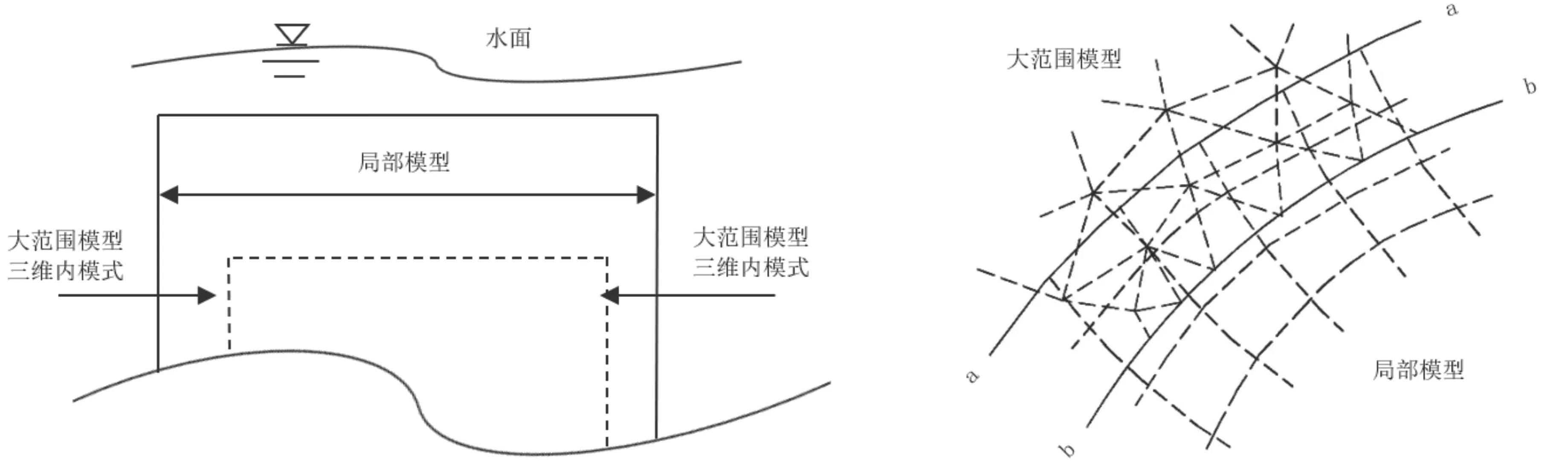
3-a 模型示意 3-b 网格示意

随后Tang等[22]基于该耦合模型成功模拟了污染流从直径为cm级的出口排放到宽度为km级的河口中并流向海域，并将模拟结果与仅采用局部模型方式计算的结果比较，证明该耦合方法的优越性。与此同时，Tang等[23]还提出一种预测沿海海流的多尺度方法，将基于HM(Hybrid method)和DDM(Domain decomposition method)的计算流体力学和地球物理流体力学模型与Chimera交叠网格[24]相结合，实现了三维不可压缩计算流体力学模型与大范围非结构化网格海洋模型的双向耦合，并提供了数值示例证明其可行性，指出多尺度空间耦合模拟有很大的发展空间和应用前景。

河口海岸泥沙输运是陆海物质循环的重要过程，对物质入海通量和全球物质循环具有重要研究意义。刘纪根等[25]认为当前泥沙输移过程随流域尺度变化的研究缺乏应有的广度和深度，总结了泥沙冲刷输运的空间尺度相关问题，探讨了不同尺度下的泥沙输运现象与规律。朱志夏等[26]针对三维泥沙数值模拟难题，采用FVCOM模型及非结构化网格二维、三维嵌套方法，建立了三维泥沙数学模型。Bai等[27]对河口海岸地区泥沙输移现象展开研究，采用有限元法FEM和有限差分法FDM相结合的方法提出海河河口模型，并在三维指标系统中引入多层模型，最后将模型应用于浑浊的华北海河河口。通过对比数值结果与实测资料，证明该多空间尺度泥沙模型与美国CH3D-SED模型具有可比性。

本节回顾了学者针对不同物理场展开的多尺度空间耦合模拟，由于小尺度和大尺度水、沙相互作用，当进行多尺度空间耦合模拟时，因大小网格的空间尺度差异性，通常会出现大范围水动力的一个网格涵盖了十至百个精细网格的现象。随着数值模拟手段的不断深入，各物理量的空间尺度跨度是逐渐增大的，例如，泥沙的大规模输运、海工建筑物的局部冲淤、泥沙颗粒运动规律等物理现象的模拟，均从宏观到微观不断深入，并且在该过程中空间尺度量级差是不可避免的。因此，如何在数值模拟中有效解决空间尺度量级差带来的问题，已成为真实模拟各物理场的研究重点及难点。

2 同一物理场多尺度时间耦合模拟研究

将不同时间尺度的物理场进行耦合模拟，预测未来时间内该物理场的真实变化，可在某种程度上满足当前对长时间变化物理现象的现实需求。虽前人曾采用统计学模型的方式对河口海岸演变进行预测并得到冲淤平衡点[27-30]，但研究性质仅限于规律，无法从机理上对长期演变进行很好地解释，并且也无法对海岸变化的具体位置进行预测。因此多时间尺度模拟预测未来长时间变化是有必要的，如泥沙输移的多尺度时间数值模拟被普遍认为是研究河口海岸地貌演变的重要工具。基于此，学者们逐渐关注各物理场的多尺度时间耦合模拟，期盼能以当前时间尺度预测未来时间内物理场变化，对厘清河口海岸水沙动力环境及相互作用机制具有重要意义[31]。

2.1 加速因子

当模拟中长期河口海岸动力地貌演变时，通常对地貌演变的时间进行加速以快速模拟动力地貌的中长期变化。基于此观念，Lesser[32]提出地貌加速因子法，这是一种用来解决地貌发展过程中出现时间尺度差异的有效方法。这一技术与Latteux[33]提出的“延长潮汐”概念相类似，旨在用短时间泥沙运动模拟实现长时间地貌演变模拟。

地貌加速因子法通过引入一个地貌加速因子(morphological acceleration factor)，有效扩展地貌时间步长以完成地貌变化的快速计算。通过乘上一个常量因子增加地形变化率，经过1个潮周期的计算，模型实际上已对n(n=fMOR)个周期的地貌变化进行了模拟，如式(1)

△tmorphology=fMOR△thyfordynamic

(1)

式中：fMOR为地貌加速因子；△t为时间步长。

由于地貌演变作用的复杂性与时空尺度多样性，当前对河口海岸动力地貌演变的理解与预测仍非常有限。Ganju等[34]首先利用ROMS模型展开河口地区多尺度时间嵌套的地貌模拟，概化了入海输沙量并引入地貌加速因子。Ganju等[35-36]也对美国Suisun湾1867年—1887年地貌冲淤开展了模拟，与实际地形变化对比预测了Suisun湾2010年—2030年际地貌演变[37]，并指出模拟年代际尺度上的地形冲淤变化难度较大。

荷兰学者们[38]利用Delft3D模型分别模拟研究了Scheldt河口西部的长时间地貌演变，实现多时间尺度耦合模拟研究。董程等[39]从黄河潮滩地貌演化角度出发，认为采用地貌加速因子后一个潮周期的地貌变化等价于10个潮周期的地貌，表明以多尺度时间方式模拟地貌变化是非常必要的。蒋超[40]系统分析了黄河入海水沙通量变化特征，揭示了黄河口不同时间尺度地貌演变的时空变化特征，为不同类型动力地貌的多尺度时间耦合模拟建立重要纽带。Luan等[41-42]阐述了主导长江口年代际地貌冲淤演变的影响因素，基于Delft3D模型建立长江口年代际地貌演变数值模型，预测了未来年代际演变的动态过程。在珠江口方面，Xing和Wu[43]基于动力地貌数值模型模拟了珠江口长时间冲淤变化过程，指明河口地形的长期演变与复杂的河网格局密切相关。吴超羽等[44]综合考虑影响珠江口动力地貌演变的驱动因子，建立长时间动力地貌演变数值耦合模型，模拟了珠江口几千年地貌、河网演变过程。考虑工程实际情况，窦希萍等[45]认为在工程初期地形冲淤变化往往较剧烈，此时不能选择大的加速因子。随着水沙动力与河床不断调整，地形冲淤变化趋缓，可选择较大加速因子以减小地貌长周期模拟计算时间。当模拟工程影响下的地貌演变时，采用随时间变化的加速因子更能提高模拟精度和计算效率。但在中长期地貌演变模拟过程中使用加速因子，模型需要设置对应尺度的上游和外海边界条件。如果仍采用实测边界条件，那么水动力过程在时间尺度上会被人为“拉长”，一个潮周期对应的地貌时间可能为数天甚至数月，显然不符合实际物理意义，因此在选择相应边界条件需要考量得当。

2.2 长期运算

由于计算资源有限，以往的数值模拟多为短时间模拟，并且大多数基于物理机制的海岸演化模型为短时间尺度下“真实性演变过程”的一个描述，难以刻画中长时间尺度的海岸演化过程和机制[46-48]。随着计算技术进步，长期运算模拟手段逐渐完善。如前所述，为预测未来长周期河口海岸水沙动力变化，常用手段是使用加速因子加快时间进程，从而缩短模拟时长。但是，Roelvink等[49]指出使用加速因子的前提是水动力计算时间步长内泥沙净输运量和地形冲淤变化很小，乘以加速因子后的地形冲淤变化不会对未来年际内地貌格局产生较大影响。

基于上述观点，学者们尝试采用长期运算手段模拟河口海岸水沙动力的长期演变，以期预测未来更长时间尺度内各物理量的变化过程。Roelvink等[50]基于二维(水平)模型模拟复杂海岸演变，认为该模型可数值再现多年海岸形态，但计算成本高且需要丰富专业知识。为克服现有海岸线模型局限性，他们开发了一种全新的海岸线模拟模型(Shorelines)，旨在预测数年到数世纪的海岸线演变。研究结果证明该模型不仅能模拟渐进的海岸变化，并且能预测未来时间尺度内海岸的根本性转变。该模型适用于局部到区域甚至全球领域，以合理的计算成本在完整生命周期中稳健跟踪海岸特征，捕捉海岸演化的复杂性，具有显著的优越性。

发展中长时间尺度的海岸演化预测方法与构建机理模型是目前国际海岸演化研究领域关注的焦点和极具挑战性的主题。Hanson等[47]对目前已有的基于短时间尺度发展的20个不同类型年代际尺度海岸演化模型进行对比分析和讨论，结果表明这类模型大多不能进行长时间尺度海岸演化过程的准确模拟。基于此，李国胜等[51]提出将一线模型(one-line model)与三维海洋动力学数值模型耦合，经过参数化后形成真正意义上的机理模型，能在长时间尺度上对河口海岸演化的驱动机制和影响机理进行深入地研究。钱继春等[52]基于潮流泥沙数学模型和滩涂动态平衡的经验关系，建立了长历时滩涂动态演变的经验动力数值模型，结果表明数值结果与实测基本吻合，能真实反映滩涂的动态演变过程。王宁舸[53]随后对江苏中部流域的河口潮滩开展1 a现场观测，建立平面二维泥沙输运及潮滩演变概化数学模型，模拟2.5 a内江苏中部潮滩变化，预测了未来年际内潮滩演变规律。程梁秋等[54]基于多年海图数据建立了相对应的数字高程模型，对伶仃洋西槽地貌展开长达15 a的数值模拟，定量分析其长期演变特征。龚政等[55]以淤长型潮滩为研究对象，建立了潮滩地貌的演变概化数学模型，预测了未来16 a内潮滩剖面的发育和演变过程，并与经典潮滩一维数值结果对比，证明建立的长期运算模型具有较高可靠性。郑钊[56]考虑黄河冲淤演变建立了数学模型以此预测未来50 a黄河的冲淤演变，并且验证了预测成果的可靠性，该预测成果对未来黄河河口治理具有重要的实际价值。

石小翠[57]从预防海洋灾害角度出发，运用SWAN模型嵌套模拟计算了中国东部海区22 a波要素，以此构成中国东部海区的波浪数据库。Liang等[58]也采用SWAN模型以当前时间尺度模拟了渤海、黄海和东海21 a的波浪要素。Langodan等[59]采用ERA-Interim全球再分析初始化WRF模式生成高分辨率区域驱动WAVEWATCH III模式，利用30 a波浪要素追算了红海波浪变化趋势。徐佳丽等[60]采用TOMAWAC模型模拟中国近海40 a的波浪要素，建立相对完整的数据库以全面描述中国海区波浪情况，以此为依据探究河口海岸地区动力演变过程。

3 多物理场单一尺度时空耦合模拟研究

河口海岸水沙动力环境的演变是个复杂的多时空尺度过程，不同时空尺度的演化过程及动力机制存在显著差异，相关研究的理论基础及技术方法也各不相同[61]。自20世纪以来，学者致力于数值模拟各物理现象，但已有研究主要聚焦于各种相对孤立的物理效应。在通常情况下，聚焦主要物理场时会采用概化方法模拟其他物理场[62]。对比学者们的模拟手段发现，聚焦主要物理场并概化次要物理场是常见且实用的研究手段。然而，现实中的物理现象并不是孤立发生的，只重点关注单一物理场会导致模拟结果与真实情况有出入。

随着计算能力不断提升，为更全面真实模拟河口海岸水沙动力环境，学者们开始在数学模型中考虑多物理场的相互耦合作用。

3.1 单向嵌套

在河口海岸地区波浪和潮流是主要驱动力，其过程复杂且呈非线性[63]。近岸区波浪在传播时会受到水流的影响，波浪自身也会产生近岸水流驱动力，两者存在耦合作用，并且波浪与潮流在时间、空间尺度上差异显著，因此研究河口海岸地区的波流相互作用具有一定意义[64]。当前波流相互作用的研究主要采用两种概化方法：一是把周期变化的潮流概化为具有某一特征流叠加到波浪运动方程中，用以模拟短时间内波流运动的变化；另一种方法是把波浪作用过程概化为潮周期中具有平均意义的波浪要素叠加到潮流运动方程中，用以描述波对流的影响。

波流模型经历了从一维到二维再到三维、由单向嵌套再到双向耦合等由简单到复杂的发展历程[65]，Longue-Higgins和Stewart[66]首先基于辐射应力概念阐明了波流相互作用机理以及波流的能量转换关系；Janssen[67]随后提出波的阻力关系，进一步丰富波流相互作用理论。在过去几十年，特别是近20 a，学者们从不同角度对波流相互作用展开细致模拟研究。Teles等[68]基于RANS方程将水流模块嵌套至波浪模块，采用任意拉格朗日-欧拉(ALE)方法模拟时变自由表面动力学，在波浪时空尺度上同时求解波流运动数值解，分析自由表面流动中波流的联合效应。许忠厚等[69]基于Delft3D建立了三维波流耦合模型，模拟了波浪作用下出水离岸堤附近的波浪与波生流间的关系，Zhang等[17]通过求解二维深度平均非线性浅水方程，在沿海水域的水动力模块加入波浪诱导的冲浪区近水平流，波流相互作用模拟结果与实测数据吻合良好。Sanchez等[70]采用二维深度平均方程求解波流作用下潮流从十几公里宽的Colombia河口流向几十万平方公里海域的地形变化，实现了基于波流相互作用的地貌演变模拟。

在水沙动力环境下，泥沙常随水流一同运动。由于水流是周期性的往复运动流，其作用下的泥沙运动也是往复运动，运动机理要比河流中单向恒定作用下的泥沙运动机理复杂得多[71]。因此，研究近岸区泥沙输移及岸滩演变具有十分重要的意义[72]。受限于计算流体力学理论不成熟，在过去的几十年中水沙模型多为非耦合模型。近20 a来得益于计算效率的提高，吴伟明等[73]通过处理连接交界面让一维和二维水沙数学模型满足水流、泥沙运动连接的边界条件，从而构建了水沙运动一维、二维嵌套模型。张华庆等[74]采用正交网格建立了珠江河口平面二维潮流泥沙数学模型，将珠江三角洲一维河网模型嵌套至珠江河口二维模型，在不同空间尺度上构建了珠江河口水沙数值模拟系统的核心计算模块。张世奇[75]在河口采用一维模式并在海岸运用二维模式，将入海口作为河海连接点，既作为一维模拟的下边界，又作为二维模拟的上边界。根据水流连续原理交替使用一维、二维尺度手段求解水位流量，采用拟合的方法使其趋于一致，由此建立一维、二维连接的冲淤嵌套模型，结果表明该模型能较准确模拟黄河口冲淤地形和输沙过程。

3.2 双向耦合

随着科学进步以及嵌套技术的成熟，信息的双向传递已经成为河口海岸水沙动力环境数值模拟研究的关键，多物理场的数值模拟方式也从单向嵌套逐步转到双向耦合。Dietrich等[76]采用区域分解并行仿真技术，在同一非结构化网格上交换网格顶点的解以实现SWAN和ADCIRC耦合，有效解决了波流相互作用的模拟难题。该模型具有高度可扩展性和通信性，在较大空间梯度上提高了局部分辨率，且能准确地模拟波流相互作用。王平等[77]基于非结构化网格同时模拟潮流和波浪，并通过参数的同步传递实现波流的耦合计算，结果表明模型对模拟近岸波流的耦合作用有着很好的精度和适用性。王文鼎等[78]采用大尺度和小尺度两种尺度的网格建立波流耦合数值模型，并将研究结论应用于部分工程实践，验证了模型的符合性、有效性和适用性。Roland等[79]基于三维水动力模型SELFE和波谱模型WWM-II，提出一种基于非结构网格的波流全耦合模型。SELFE和WWM-II模型间的耦合是在源代码级别进行的，在共享相同子域的基础上并行MPI和域分解，从根本上保证并行效率和避免插值。Roland等[79]随后将模拟结果和现场资料比较，结果表明即使在复杂的实际环境下，耦合模型也能捕捉到不同尺度下波流相互作用过程。

在水流问题的研究上，王智勇等[80]提出耦合边界水位预测校正法，由此建立一维和二维耦合水动力模型。在任一时间步计算时先在耦合连接处预测一维和二维水位边界条件，再根据耦合边界处的流量计算结果及当地水力参数对水位边界条件反复校正，直至耦合连接条件满足计算容差。顾杰等[81]基于MIKE-FLOOD模块建立秦皇岛入海河流与近岸海域间的一维、二维耦合河流-海岸水动力模型，系统研究了秦皇岛海域入海河流的水动力特性。来志刚[82]在珠江口实现了一维河网、三维河口的水动力耦合模拟，成功将一维、二维水动力及泥沙连接模型基本条件和计算方法扩展至一维、三维水动力模型的耦合模拟。Zhou等[83]基于质量守恒准则，耦合了一维河网模型与三维河口模型，为珠江三角洲的水环境监控提供可靠依据。同时，Lai等[84]着眼于长江中游复杂河湖大水系，提出一种新的耦合水动力模型CHAM，为河口海岸地区的复杂流态提供了有效模拟工具。

准确描述河口海岸的水流运动是合理描述泥沙运动的基础，目前相关学者在泥沙数值模拟方面已开展了相关研究并取得一定成果[85]，张修忠等[86]指出对于解决河口海岸这类具有多空间尺度的水沙问题，采用单一模型不仅困难、费时，且不易掌握不同区域矛盾的主要特征。基于此张修忠等[86]利用有限元的非结构化网格特点和子结构叠加的概念，建立了一种虚拟过度区间的一、二维耦合算法。苏东升等[87]基于CFD-DEM 方法建立水沙运动耦合模型，张华庆等[88]考虑水沙相互关系建立了一维、二维耦合的水沙模型，将河口地区视为重点区域进行计算。张鹏飞和陆建刚[89]研究了通江湖泊与外部江河的水沙交换过程，基于二维非稳态水流和泥沙耦合数学模型，模拟了鄱阳湖与外部江河的水沙交换过程。Li等[90]基于三维水动力模型与泥沙运动模型，耦合模拟了北部湾海岸地区沙波的迁移过程，模拟结果与实测基本吻合，表明多场耦合模型可以模拟现实中的沙波迁移规律。在验证耦合模型能较好模拟水沙运动后，Shen等[91]考虑河口和沿海地区水域悬浮沉积物浓度的高变异性特征，建立了泥沙模型与开源TELEMAC系统耦合的平衡模型。叶涛焱[92]为探究杭州湾人类活动影响下的悬沙浓度，建立了三维水沙数值耦合模型ESed，分析了杭州湾湾口悬沙动力与潮滩变化的互馈机理。

由此可见，在多物理场单一尺度时空耦合数值模拟中，通常在求解控制方程时考虑多因子的相互影响。本节总结了学者在河口海岸地区波浪、潮流以及泥沙方面的研究成果，说明了考虑不同物理场的相互作用能更真实反应河口海岸的水沙动力环境的变化。但目前数值模拟多为单一尺度时空耦合，在准确刻画不同时空尺度下各物理场间的相互作用上仍有所欠缺。

4 模拟难题与建议

在河口海岸水沙动力环境的数值模拟中，模拟手段从单独模拟到单向整合再发展至双向耦合。以往的模型大多仅实现信息单向传递，即给定初始、边界条件时A模型先计算，再将A模拟结果传至B模型，此时B模型结果并未反馈给A模型。但是，较为理想的是结果相互反馈：A将结果传递至B，B同时反馈至A，循环迭代直到各物理场的计算达到稳定。在整个模拟过程中，数据在每一时间步都进行交换，据此实现两个模型间的实时双向耦合。

实际河口海岸水沙动力环境是多物理场相互作用的结果，早在1993年Orton和Reading[93]就提出河口系统每一个地貌单元并不是独立的个体，而存在频繁的物质交换和相互作用过程。考虑不同物理场相互作用时，数据相互反馈使耦合模拟结果更精确。随着社会发展及行业需求，研究重点、热点也更加聚焦于多物理场的多尺度时空耦合模拟，河口海岸地区多物理场间的相互作用问题也越来越广泛受到人们的重视，例如：海冰、波浪、水流的相互作用[94]，波浪、水流、泥沙的相互作用[95]，风、波浪、水流的相互作用[96]，大气、海浪、海流的相互作用等[97]。与此同时，多物理场相互作用现象越发复杂，水沙动力与结构物响应、波浪-海床-结构物[98]相互作用等问题也逐渐突出，多尺度计算已经发展成为一个具有自身特征的学科，是构成人们探索和理解物质世界多尺度问题的基础[99]。因此，在求解多物理场相互作用时，如何客观描述控制方程是提高数值模拟精度、实现多尺度时空耦合的研究重点，也是亟待解决的关键问题。

受限于计算技术及耦合算法的难度，多物理场的全耦合模拟尚未完全实现。结合现今技术手段，采用以下三种方法实现模型间耦合较可行。第一种方法是将两种模型代码直接合并，基于内存实现模型间的数据传递，但通常两个模型是独立开发，因此数据的交互具有一定难度。第二种方法是利用现有通信工具或协议如MPI，但该方法需模型开发人员具备专业知识。第三种方法是使用模型耦合工具提供自动传输数据接口，这种方法能极大减少模型开发期间修改代码的工作量，并且非专业技术人员也能实现模型接口配置，相比下具有更优性。虽第三种方法更具优越性，但关于耦合模型接口的搭建，实现数据的自动传输难度很大。因此如何开发模型耦合工具及使用好该工具，实现信息交互、耦合的自动化以及模型结果的相互反馈是学者们非常期待的。

5 结语

河口海岸是地球四大圈层交汇、能量流和物质流的重要聚散地带，既是流域物质的归宿，又是海洋的开始，生态环境极其敏感、脆弱。高精度数值模拟手段是未来河口海岸水沙动力耦合作用机理及其环境影响效应评估等研究的主要手段和发展趋势。本文回顾了河口海岸地区潮流、波浪及泥沙等多物理场间的耦合作用及同一物理场下多尺度空间、时间耦合作用，探讨了多尺度时空耦合过程中周期量级差、尺度量级差、各物理场间的相互耦合、多尺度时空耦合技术以及多物理场多尺度时空耦合等关键难题，指出现阶段实现河口海岸多物理场多尺度时空数值耦合的模拟仍面临许多挑战，急需展开深入系统研究和工程实践。