细沙短时射流冲刷的FLUENT与FLOW-3D数值模拟方法比较

张翔宇，倪福生，顾 磊

(1.河海大学 疏浚技术教育部工程研究中心，常州 213022；2.河海大学 机电工程学院，常州 213022)

在疏浚工程中，耙吸挖泥船常配有射流冲刷系统，射流冲刷系统可以有效降低耙头的切削力、预防耙头堵塞、破岩切割等以提高耙吸挖泥船耙吸效率[1]。在数值模拟方法出现之前，研究人员需进行大量实验为提高射流冲刷效率提供依据，Aderibigbe等[2]采用圆形喷嘴进行了二维垂向射流冲刷实验。

但随着流体动力学的发展，出现了多种数值模拟方法，研究人员在实验基础上配合数值模拟的方法可有效地减少成本，提高灵活性并取得了一定的成果，现阶段在一、二维泥沙数值模拟方面已较为成熟，三维模型也能用来解决一些实际问题[3]。钱忠东等[4]运用FLUENT欧拉模型探索了水体作用力以及孔隙率对冲坑形态的影响；槐文信等[5]运用FLUENT建立了基于希尔兹数的推移质泥沙输运模型并采用动网格技术捕捉射流冲刷时水沙交界面处变化；刘思源等[6]基于FLUENT欧拉多相流模型探究了泥沙粒径以及射流速度对沙床的影响；Liu等[7]运用FLOW-3D建立了局部泥沙冲刷三维数值模型来得到精准的冲刷形态；黄佳丽等[8]采用FLOW-3D软件确定了泥沙模型中影响射流冲刷泥沙过程的关键参数；净晓飞等[9]利用FLOW-3D软件分析海上风电单桩基础的冲刷过程及防冲刷措施的效果；刘成林等[10]采用FLOW-3D泥沙冲刷模型研究水平射流冲刷，探究了冲刷平衡时冲坑深度影响因素。李伟等[11]利用FLOW-3D探究了喷管下射流的水动力条件、泥沙运动与冲刷坑的发展变化规律。

通过分析前人对射流冲刷问题的研究发现，其大多是针对长时间射流且射流稳定时冲坑形态，对于短时射流动态冲坑尺寸的研究较少，且研究主要针对二维射流冲刷，同时研究人员运用FLUENT和FLOW-3D进行数值模拟较多，对于细沙三维短时圆柱射流冲刷问题，何种研究方法更好尚无明确定论。本文对比FLUENT与FLOW-3D在网格划分、水相控制、泥沙相模拟、水沙相互作用方面区别，并对FLUENT与FLOW-3D两者自身对泥沙的起动、沉降、对流、堆积进行设置，最后将FLUENT与FLOW-3D模拟结果与实验所得结果进行比较研究，最终可以得到较为适合细沙短时射流的数值模拟方法，为以后细沙短时射流冲刷研究提供一定参考。

1 几何模型

实验在透明水槽中进行，实验装置如图1所示，其中射流区域长、宽、高均为1.5 m，沙床高0.3 m，喷嘴直径2 mm，喷嘴出口距离沙床表面0.1 m，射流喷嘴固定于水箱底部并浸没于水中，底部为沙床表面。本文针对耙吸挖泥船前部射流冲刷系统对河道的疏浚，所以采用的泥沙为长江口河道中挖掘的天然沙，并且对长江口泥沙进行土力学测试得到其泥沙的特性，得到实验用沙床条件如下：粒径0.13 mm细沙、含水率25.6%，容重为16.503 kN/m3，干密度为1.684 g/cm3、天然密度为2.115 g/cm3，射流速度v=10 m/s、15 m/s、20 m/s。实验采用秒表计时，在四个地方分别记录射流1 s、2 s、4 s、8 s时冲坑形态，冲坑深度采用直尺测量，冲坑面积与体积采用照片图像处理方法得到。

图1 实验模型

FLUENT与FLOW-3D数值计算区域与实验模型相一致，计算区域上部为水相，下部为泥沙相，喷嘴位于计算区域中央，如图2所示。在FLOW-3D模型建立时，模型上端可添加挡板，有助于泥沙冲刷模型计算，而FLUENT则无需建立挡板。

2 理论模型

对于三维圆柱射流冲刷数值模拟问题，首先对几何模型进行网格划分，之后分析水流冲击情况，尤其需要分析水冲击泥沙后，泥沙的输移情况。泥沙的输移主要包括：(1)起动：泥沙被水流带起而悬移于水中;(2)沉降：悬移泥沙受重力落下;(3)对流：悬移泥沙随水流移动;(4)推移质输移：泥沙沿河床滚动或跳动。

FLUENT与FLOW-3D在以上四方面存在区别，表1为FLUENT与FLOW-3D的对比表。

表1 FLUENT与FLOW-3D对比

FLUENT与FLOW-3D网格划分存在区别。对于规则物体，两者均采用结构网格进行划分；但对于不规则物体，FLUENT主要采用非结构网格，并可在水沙交界面处采用动网格技术精确描述水沙交界处运动变化，而FLOW-3D采用FAVOR技术，使曲面模型可以用矩形网格描述，描述水沙分界面较轻松。

对于水相控制，由于圆柱射流湍流强度低、雷诺数低、剪切区强烈，所以本文FLUENT水相控制湍流模型选择RNGk-ε湍流模型，RNGk-ε中k与ε方程分别为

(1)

(2)

式中：Gk和Gb为湍动能，分别是由平均速度梯度和浮力影响引起的；C1ε、C2ε、C3ε为常数，取值为C1ε=1.44，C2ε=1.92，C3ε=0.09。FLOW-3D对水相控制同样采用RNGk-ε湍流模型。

FLUENT与FLOW-3D中泥沙重力是影响泥沙沉降的主要因素，需要开启重力模型来表示泥沙的沉降，及z轴重力加速度-9.8 m/s2。由于泥沙并非液体，一定体积的泥沙中存在着不容忽视的孔隙，而孔隙率是通过实验测量含水率后根据土力学[12]知识换算所得，FLUENT中泥沙孔隙率0.397；FLOW-3D中泥沙临界体积分数=1-泥沙孔隙率，为0.603。FLOW-3D中可设置泥沙水下休止角，本文为45°。

FLUENT与FLOW-3D对水沙相互作用描述存在差异。FLUENT欧拉模型把连续相与分散相视为连续的一体，两种流体存在于同一空间中并相互渗透，但有不同的体积分数，并且对水和泥沙相分别建立控制方程，通过压力和相间交换系数的耦合来计算求解，其连续方程为

(3)

式中：q分别代表流体相和泥沙相；αq为各相的体积分数；ρq为各相密度；vq为各相速度；mij为从相j到相i的质量传递；Si为质量源项，其缺省值为零。

FLUENT动量守恒定律可描述为任意微元体流体动量对时间的偏导数等于外界作用于该微元体上的各力矢量之和[13]。动量方程可表示为

(4)

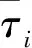
FLUENT欧拉模型边界条件设置：入口边界选择速度入口，其湍动能k和湍流耗散率ε分别按下式计算

(5)

(6)

式中：μin为入口速度；I为湍流强度，I=0.16(ReDH)-1/8，DH为水力直径；Cμ为经验常数，取值为0.09；由于出口处为自由水面，选择出口边界为自由流出界面；其余为固体壁面。

FLOW-3D泥沙冲刷模型是通过预测泥沙的侵蚀、对流、沉积来模拟泥沙运动的，同时考虑多孔介质表面对流体的阻碍，对式(5)、式(6)连续、动量方程添加附加项。

(7)

(8)

式(7)中，使用笛卡尔坐标系时，取R=1，ξ=0。RSOR是质量源项，可模拟水流经沙床这种具有多孔特性的表面的过程。RSOR/ρ则表示网格中流体的体积源。式(6)中bx、by、bz为流体流经多孔介质时的损失项，即水流经泥沙时的流动损失，提高泥沙和水相互影响的准确性。

FLOW-3D泥沙冲刷模型中泥沙挟带系数的设置可以影响泥沙的起动情况，当沉积物受力大于临界剪切应力时，泥沙会随之起动，且泥沙挟带系数α对冲刷速率的影响较大。可根据Winterwerp[15]的无量纲侵蚀速率公式

(9)

式中：α为挟带系数；θ为床面希尔兹数；θcr为临界希尔兹数；d*为泥沙颗粒的无量纲粒径，可得到挟带系数，只改变挟带系数，得到冲坑深度与时间变化，可知挟带系数增大，冲坑深度和冲刷速率增大，所以本文选择挟带系数0.018。

FLOW-3D泥沙冲刷模型中泥沙推移质系数的设置可以影响泥沙的推移情况，当沙床传输所受剪切力大于临界剪切应力时，沉积物会向四周进行运动，且泥沙推移质系数β对泥沙传输量影响较大。可根据推移质输沙率公式[16]

(10)

其中：Φ是无量纲的推移质输沙率；β是推移质系数；θ为床面希尔兹数；θcr为临界希尔兹数；d*是泥沙颗粒的无量纲粒径，可得到推移质系数，改变推移质系数发现，随着推移质系数增加，冲坑深度先显著增加后增加减少，所以本文推移质系数选择0.5。

3 数值模拟结果对比

3.1 冲坑形态对比

图3为射流速度15 m/s，射流冲刷8 s时FLUENT、FLOW-3D、实验分别所形成的的冲坑形态图。

3-a FLUENT 3-b FLOW-3D 3-c 实验

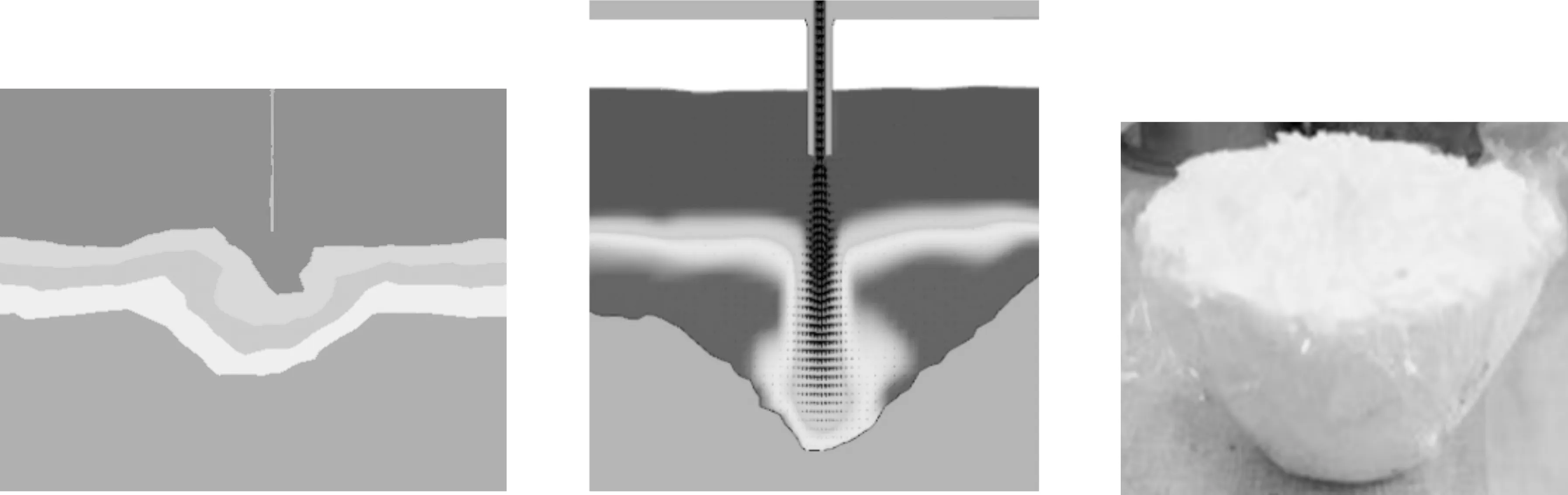
从图3中可以看出，FLUENT冲坑形态呈现漏斗状，上部直径较大，向下逐渐减小，在坑周围出现不明显隆起，这与实验冲坑形态图较为吻合，但冲坑深度与冲坑范围相对实验结果明显偏小；FLOW-3D冲坑形态与FLUENT相近，但冲坑深度和冲坑范围相对于FLUENT结果明显更深且范围更大。进一步分析FLUENT与FLOW-3D冲坑形态与实验的吻合度，做出FLUENT、FLOW-3D的(ε/εm)与(r/b)关系图，与实验结果进行对比，其中ε、εm、r、b为冲坑深度、冲坑最大深度、冲坑半径、冲坑深度一半处冲坑半径，如图4所示。

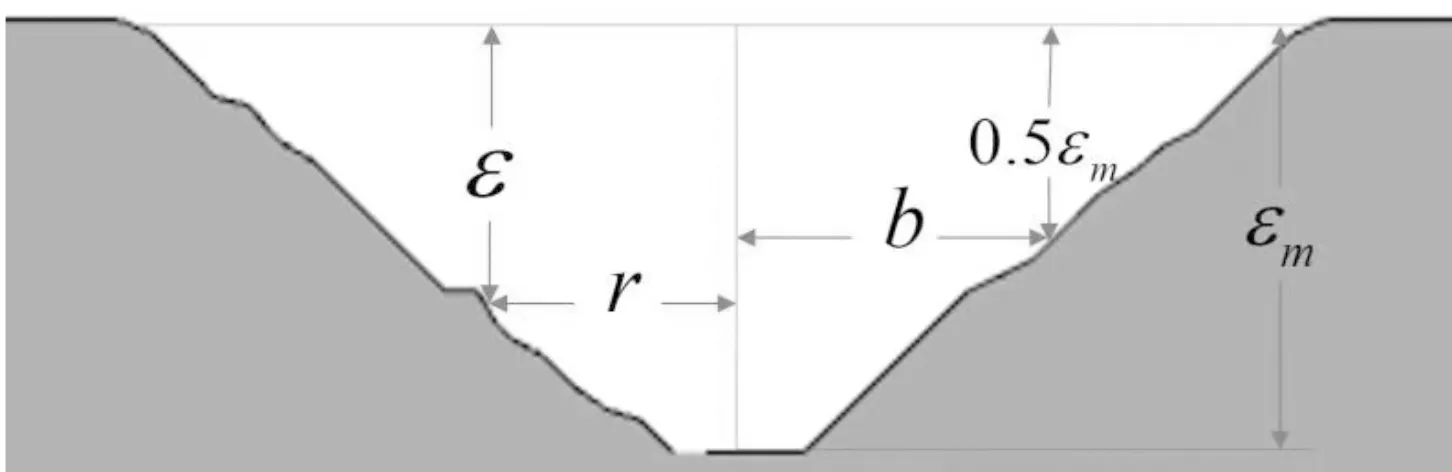
图4 冲坑尺寸

从图5中可以看到，FLUENT冲坑深度最大处在r/b=-0.25处，而并不是0处，表明FLUENT冲坑形态左右不对称，且左侧斜坑角度为55°，明显大于右侧斜坑角度50°，而实验冲坑形态呈现左右较为对称，斜坑角度为46°；FLOW-3D冲坑深度最大处在r/b=0处左右，且冲坑左右较为对称，左侧与右侧斜坑角度为45°左右，与实验所得冲坑形态较为吻合。

5-a FLUENT 5-b FLOW-3D

同样，对于流速10 m/s、20 m/s时FLUENT、FLOW-3D与实验的冲坑形态对比与15 m/s情况类似。

由此可知，FLOW-3D相较于FLUENT的冲坑形态与实验结果更为吻合，其主要原因是：FLOW-3D对泥沙采用独特运动物体功能划分网格，将泥沙看做个体，保证颗粒运动，网格不动，对泥沙运动描述较准确，且可以对泥沙的水下休止角进行设置以保持斜坑角度与实验一致；而FLUENT只设置泥沙的起动，对泥沙起动后的运动没有进一步描述，导致泥沙运动不规律。

3.2 冲坑深度对比

对于流速15 m/s，针对FLUENT与FLOW-3D冲坑范围的不同，提取两者相同时间下的冲坑深度，得到冲坑深度随时间的变化曲线图，并与实验结果进行对比，由于实验过程容易出现误差与一些偶然因素，所以分别做两组实验以保证实验结果的准确性。

由图6可知，两组实验数据得到冲坑深度均呈现先迅速增长后缓慢增长趋势。FLUENT与FLOW-3D冲坑深度结果显示：在0～1 s内FLUENT与FLOW-3D冲坑深度迅速增加，与实验结果大致吻合，FLUENT与FLOW-3D冲坑深度略大于实验深度，其原因是在射流开始阶段，FLUENT与FLOW-3D可以一直模拟较稳定射流，而在实验中，实验初期的射流并不稳定，所以FLUENT与FLOW-3D数值较大；在1～8 s，FLUENT冲坑深度不再明显增加，最终逐步稳定在36 mm左右，与实验趋势不同；在1～8 s，FLOW-3D冲坑深度的增长速率相较0～1 s减小，冲坑深度逐渐增大，与实验结果较为吻合。同样，对于流速10 m/s、20 m/s时FLUENT、FLOW-3D与实验的冲坑深度对比与15 m/s情况类似。

分析其主要原因是FLUENT中没有对泥沙的沉降、推移进行描述，水流将泥沙冲起后，只考虑水对泥沙作用，而不考虑泥沙之间相互作用，导致泥沙沿斜坑向外运动较困难，使冲坑深度不再增加；而FLOW-3D中设置了泥沙的悬浮和推移，保证泥沙随着射流冲刷而逐渐向坑外推移。

3.3 冲坑面积、体积对比

为进一步分析FLUENT、FLOW-3D冲坑范围与实验吻合情况，绘出流速15 m/s下FLUENT与FLOW-3D得到的冲坑面积与体积随时间变化图，并与两实验结果进行对比，如图6所示。

由图7、图8中实验1与实验2所得冲坑面积、体积可知：在0～1 s，冲坑面积、体积迅速增加；在1～8 s，冲坑体积、面积与时间大致呈线性关系。

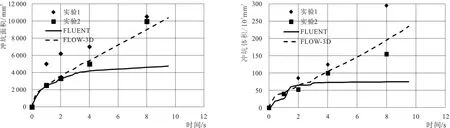
图7 冲坑面积对比图

由图7、图8中FLUENT曲线可知，在0～1 s，FLUENT模拟的冲坑面积、体积增长较为明显；在1～8 s，冲坑面积、体积随时间无明显增长，表明冲刷在1 s以后已经趋于稳定。FLUENT在0～1 s所得结果与实验较为吻合，而在1～8 s，冲坑面积、体积与实验结果差别明显，在8 s时，冲坑面积、体积只有实验的40%。同样，对于流速10 m/s、20 m/s时FLUENT、FLOW-3D与实验的冲坑面积、体积对比与15 m/s情况类似。

分析其主要原因是FLUENT欧拉模型将泥沙视为连续介质，像水银一样，会明显受到水流的影响，冲坑会随着水流运动而出现左右波动有时甚至不成坑型，导致冲坑只是位置上改变而面积和体积没有变化，同时在1 s以后，FLUENT的冲坑深度不再增加，同样冲坑面积、体积没有明显变化。

由图7、图8中FLOW-3D曲线可知，在0～1 s，冲坑体积变化速率较快，在1～8 s，体积变化速率渐渐减缓，其趋势接近线性增长。可以得出：FLOW-3D的冲坑体积和冲坑面积随时间变化趋势与实验结果较为吻合；对于实验1的第8 s冲坑体积误差较大，其主要原因为冲刷点的泥沙不均匀和测量等误差造成；在FLOW-3D中可以对泥沙对流和推移进行设置，使泥沙运动呈现一定规律性。

4 结论

运用FLUENT与FLOW-3D对细沙短时圆柱射流问题进行数值模拟分析。结果显示：由于FLUENT欧拉模型将泥沙相视为连续介质，且只能通过设置起动条件控制泥沙起动过程，对其沉降、堆积过程难以描述，故模拟结果与实验存在较大差别；而FLOW-3D中的泥沙模型，将泥沙看作个体，对其起动、悬浮、沉降和推移过程均可准确描述，故模拟所得冲坑形态以及冲坑深度、截面积和体积的发展过程，都与实验结果吻合度较高。总之，FLOW-3D软件用于模拟细沙短时射流冲刷泥沙过程更为适合。