基于磁流变半主动悬架的整车姿态补偿控制

汪若尘，盛富鹏，丁仁凯，孟祥鹏，孙泽宇

(1.江苏大学 汽车与交通工程学院，江苏 镇江212013；2.江苏大学 汽车工程研究院，江苏 镇江 212013)

半主动悬架能够根据不同行驶路况对整车悬架系统的阻尼值进行实时调节，具有主动悬架的通用性和适应性，并且能耗极低.半主动悬架阻尼调节的形式主要有2种：一种是通过电磁阀开关或电动机旋转改变节流口开度[1]；另一种是应用功能材料如磁流变材料作为减振器液，通过改变流体的黏度系数实现减振器阻尼可调[2].但前者相较于后者存在结构复杂、体积大、频响低等弊端[2].因此，国内外专家学者对磁流变半主动悬架进行了广泛研究.

当前对磁流变半主动悬架的研究主要集中在磁流变阻尼器逆模型的构建及其控制方法上.磁流变减振器的数学模型主要包括Bouc-Wen滞后模型[3]、Neural network模型[4]、Bingham模型[4]和多项式模型[5].相比其他数学模型，多项式模型能够较为精确地反映磁流变阻尼器的非线性特性，并且其逆向动力学模型更容易被推导，利用开环系统更容易获得理想的阻尼力[5].因此，该模型的应用有利于对磁流变减振器进行实时控制.在控制方法方面，众多控制方法被应用到磁流变半主动悬架的控制上，如天棚控制[6]、滑模变结构控制[7]、模糊控制[8]以及多种控制方法的复合控制.但是，当前研究主要集中于1/4半主动悬架系统控制问题，鲜有涉及基于磁流变半主动悬架的整车姿态问题.同时，车辆在行驶过程中产生的垂向、俯仰和侧倾运动互相影响，使车身产生扭转影响乘坐舒适性[9]，通过对各悬架单独进行状态估计并控制，无法解决不同自由度运动对车身姿态的影响.为此，许多专家学者对整车动力学进行解耦或分层控制研究或对悬架系统与制动系统及转向系统的协同控制进行研究，但这些方法较为复杂，并且未考虑减振器的动态特性和车辆的行驶工况，控制效果难以有效保证.

为了解决上述问题，笔者构建整车动力学模型以及磁流变阻尼器多项式模型，设计结合状态观测的磁流变半主动悬架整车姿态补偿控制方法，包括姿态补偿控制算法、磁流变减振器控制算法与精确状态观测器设计方法.通过仿真分析，验证所设计的磁流变减振器控制算法的有效性，并通过硬件在环试验进一步对其进行验证.

1 整车模型构建

1.1 整车Adams模型

通过Adams/Car软件，构建整车的精确多体动力学模型，主要包括悬架系统模型、车架模型以及轮胎模型，并适当调整转向系统和传动系统的性能参数，以满足对所需车型的要求.通过对所建模型中底盘硬点数据的测量和收集，获得整车底盘相关的性能参数，在Adams/Car中建立的整车多体动力学模型如图1所示.

图1 整车多体动力学模型

1.2 磁流变减振器多项式模型

试验测得磁流变减振器外特性如图2所示.其中：F为减振器阻尼力；v为磁流变减振器的速度.

图2 磁流变减振器外特性

从图2可以看出：磁流变减振器存在明显的滞回特性，即其加速度方向不同时，在减振器速度较低情况下减振器的阻尼力差别明显.因此，根据减振器的加速度正负情况，将试验测得的减振器外特性划分为上、下支.利用Matlab中Curve Fitting工具箱对以上磁流变减振器的速度-力特性曲线进行分支拟合.综合考虑计算复杂性和拟合精确性，采用分子为5次、分母为2次的分式多项式函数作为拟合函数，即

(1)

式中：p1-p6、q1、q2均为待拟合系数.

式(1)多项式模型拟合曲线如图3所示，其中：F1为减振器上支的阻尼力；F2为减振器下支的阻尼力.无论上支还是下支，由多项式模型获得的速度-力特性曲线与试验数据点基本吻合.

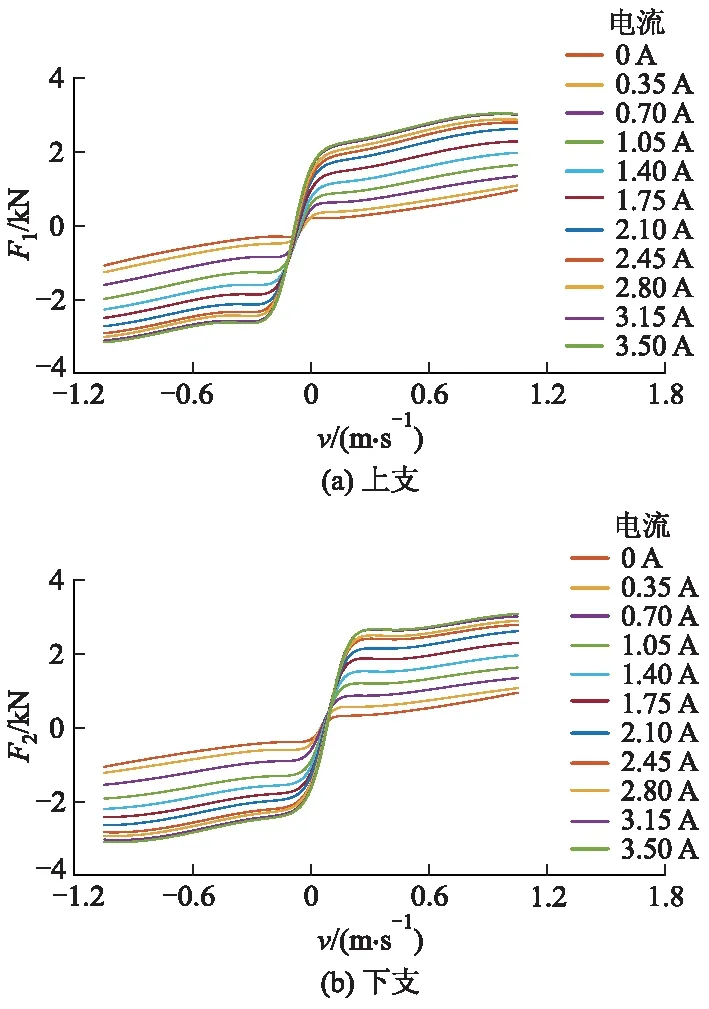
图3 多项式模型拟合曲线

2 整车半主动悬架控制算法设计

所设计的磁流变半主动悬架姿态补偿控制算法模块主要包括姿态补偿控制算法、磁流变减振器控制算法以及悬架状态观测器模块，整车半主动悬架控制过程如图4所示.

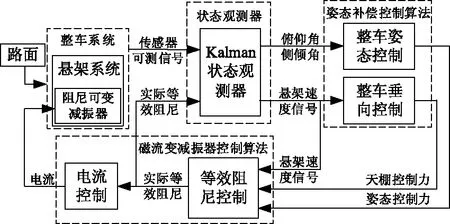
图4 整车半主动悬架控制过程

2.1 姿态补偿控制算法设计

姿态补偿控制算法分为垂向控制算法与姿态控制算法.考虑到行驶工况和路况差异将造成车辆在行驶时产生垂向运动、俯仰运动和侧倾运动，造成车身姿态的变化，本研究基于整车悬架系统，对整车车身姿态进行控制，计算悬架的姿态补偿控制力以改善车身俯仰和侧倾运动.

2.1.1整车垂向控制算法设计

利用天棚控制获得悬架垂向控制力，改善车辆舒适性，天棚控制产生的各悬架垂向控制力为

(2)

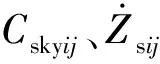
2.1.2整车姿态控算法设计

在整车姿态控制算法中，以俯仰角φ和侧倾角θ为输入信号，以各悬架的姿态补偿力Δfij为输出信号，设计了一个二输入四输出的模糊控制器.模糊控制中各输入(φ、θ)以及输出(Δfij)的基本论域均设置为[-6,6].该模糊控制器的模糊控制规则如图5所示，其中横、纵坐标值为离散度的值.

图5 模糊控制规则

考虑到实际仿真中，车身俯仰角的变化范围为-0.05～0.05 rad，侧倾角的变化范围为-0.1～0.1 rad，因此，将俯仰角量化因子K1设定为120，侧倾角量化因子K2设定为60，同时，考虑过大的车身姿态补偿力Δfij会对整车磁流变半主动悬架系统的控制效果造成不利影响，通过多次仿真，确定各车身姿态补偿力应控制在120 N以内，从而，设置各车身姿态补偿力Δfij的量化因子K3为20.

2.2 磁流变减振器控制算法设计

为了让磁流变减振器同时输出垂向控制力和姿态补偿力，以抑制车身垂向运动和姿态运动，提出由两者决定的磁流变减振器可输出等效阻尼，并考虑了磁流变减振器实际工作中可输出等效阻尼的范围，设计了各悬架系统中磁流变减振器控制算法.

2.2.1等效阻尼控制算法设计

根据垂向控制力fsij与姿态补偿力Δfij，计算各悬架的等效阻尼Ceqij，即

(3)

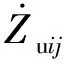
计算各磁流变减振器实时加速度，若加速度为正,则为下支状态，相反为上支状态.若处于上支状态，将当前等效阻尼Ceqij与磁流变减振器此时所能输出的最大等效阻尼C-max和最小等效阻尼C-min进行比较分析，以确定其输出的实际等效阻尼Cij，若处于下支状态，判断方法相同，具体规则如下：

(4)

(5)

式中：C+max、C+min分别为处在下支状态时磁流变减振器所能输出的最大等效阻尼和最小等效阻尼.

为了获得磁流变减振器等效阻尼的范围，对其上下支的力学多项式模型进行处理，得出不同电流下，实际等效阻尼Cij与各磁流变减振器速度vij的关系，即

(6)

式中：r0-r7为多项式相关系数.

2.2.2磁流变减振器控制电流计算

通过对磁流变减振器多项式拟合参数进行分析可知，无论磁流变减振器处于上支状态或下支状态，式(6)中系数r0-r7与电流Iij可拟合为线性关系，具体关系如下：

rm=amIij+bm，m=0,1,…,7,

(7)

式中：am、bm为拟合系数.

考虑到am和bm都已拟合确定，等效阻尼Ceqij仅与控制电流Iij及减振器速度vij有关.经过推导，可得到以计算输入磁流变减振器的控制电流为

(8)

2.3 整车悬架精确状态观测器设计

由于传感器技术的限制和信号测试的复杂性，悬架系统中速度信号一般较难测得，但是速度信号是上述控制方法中的重要反馈信号.为了对磁流变减振器进行更精确控制，基于卡尔曼滤波原理，考虑等效阻尼的影响，设计了整车悬架精确观测器.

2.3.1整车悬架系统状态描述方程构建

整车悬架系统模型如图6所示，其中：ms为车辆的簧载质量；msij、muij分别为各悬架的车辆簧载质量、簧下质量；Iθ、Iφ分别为侧倾转动惯量和俯仰转动惯量；Zrij、Zuij、Zsij分别为各悬架的路面位移、簧下质量中心处的位移、簧上质量中心处的位移；a、b分别为车辆前轴、车辆后轴与质心之间的距离；c和d分别为车辆右车轮、车辆左车轮与簧上质心之间的距离；Fij为每个悬架控制力；Ksi和Kti分别为各悬架的弹簧刚度和轮胎刚度；Csij为各悬架减振器的阻尼系数.

图6 整车悬架系统模型

根据整车悬架系统模型，建立了如下整车运动微分方程.质心处的运动微分方程为

(9)

各悬架中簧下质量部分的运动微分方程为

(10)

各悬架中，螺旋弹簧与减振器产生的合力为

(11)

由式(9)-(11)可得整车状态微分方程：

(12)

2.3.2精确状态观测器设计

将整车状态微分方程(12)进行精确离散化后得到如下离散化系统方程：

(13)

式中：X(k)为k时的状态变量；Φ为离散化系统的状态转移参数矩阵；G为离散化系统的噪声驱动参数矩阵；W(k-1)为k-1时，均值为零矩阵，方差为Q的白噪声输入；Y(k-1)为k-1时的状态观测变量；H为离散化系统状态观测参数矩阵；V(k-1)为k-1时观测产生的噪声，假定该噪声和输入白噪声不相关.

根据系统在上一状态的最优估计结果X(k-1|k-1)对系统的目前状态量进行预测，结果为X(k|k-1)，即

X(k|k-1)=ФX(k-1|k-1).

(14)

然后，依据系统上一状态的协方差P(k-1|k-1)，更新获得目前系统状态的预计偏差P(k|k-1)，计算公式为

P(k|k-1)=ФP(k-1|k-1)ФT+GQGT.

(15)

根据目前系统状态的预计偏差P(k|k-1)，得出目前状态下卡尔曼增益为

Kg(k)=P(k|k-1)HT/(HP(k|k-1)HT+R)，

(16)

式中：R为观测噪声的方差.

通过目前状态下卡尔曼增益，实现对离散系统的更新，从而获得目前系统状态的最优估计结果X(k|k),即

X(k|k)=X(k|k-1)+Kg(k)(Y(k)-

HX(k|k-1)),

(17)

式中：Y(k)为k时的状态观测变量.

通过式(18)计算获得目前状态下协方差P(k|k)以实现下一时刻系统状态的最优估计，即

P(k|k)=(I-Kg(k)H)P(k|k-1)，

(18)

式中：I为单位矩阵.

3 控制效果分析

依据所建立的Adams整车多体动力学模型以及Simulink中整车车身姿态补偿控制器，分别对悬架精确状态观测器的估计性能以及姿态补偿控制算法的控制效果进行仿真分析，从而验证所设计控制算法的有效性.

3.1 悬架精确状态观测器估计分析

通过整车悬架精确观测器，各悬架系统中速度信号得以获取，包括各悬架中簧上质量部分的绝对速度和减振器的相对速度，以实现对整车磁流变半主动悬架系统的准确控制.观测器对信号的估计精度将直接影响控制效果的优劣，因此，下文将以左前悬和左后悬为例，假定车辆以72 km·h-1匀速行驶在C级路面上，给出经悬架精确状态观测器获得的速度信号估计效果，并对其进行具体分析.车身绝对速度、悬架相对速度估计效果对比分别如图7、8所示，其中：t为时间；vbLF、vbLR分别为左前悬、左后悬车身绝对速度；vsLF、vsLR分别为左前悬、左后悬减振器相对速度.

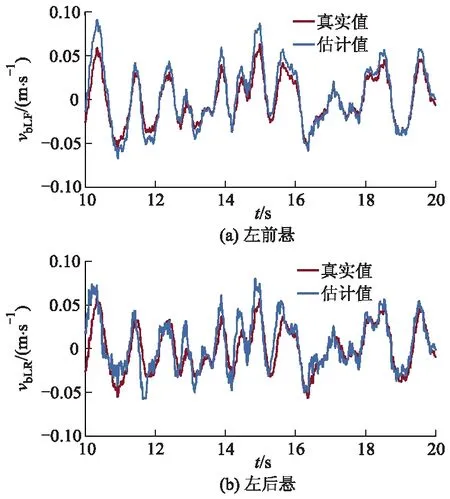
图7 车身绝对速度估计结果对比

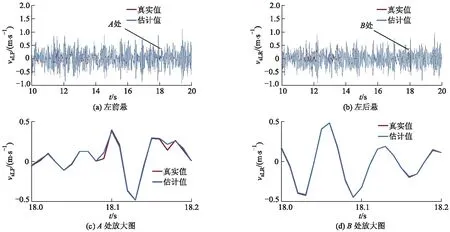
图8 悬架相对速度估计结果对比

在无观测器和带观测器的状态下，分别对车身绝对速度及悬架相对速度的估计效果进行对比仿真，结果表明：本研究设计的整车悬架状态观测器的估计精度能够满足要求，10 s之后，速度信号的估计误差将控制在真实值的10%以内.

3.2 整车悬架控制效果分析

为了验证所设计的控制算法的控制效果，通过联合仿真，将其与普通被动悬架进行对比.假定车速以72 km·h-1在C级路面上匀速行驶，质心垂向加速度、俯仰角加速度和侧倾角加速度仿真结果分别如图9-11所示，其中：av为质心垂向加速度；

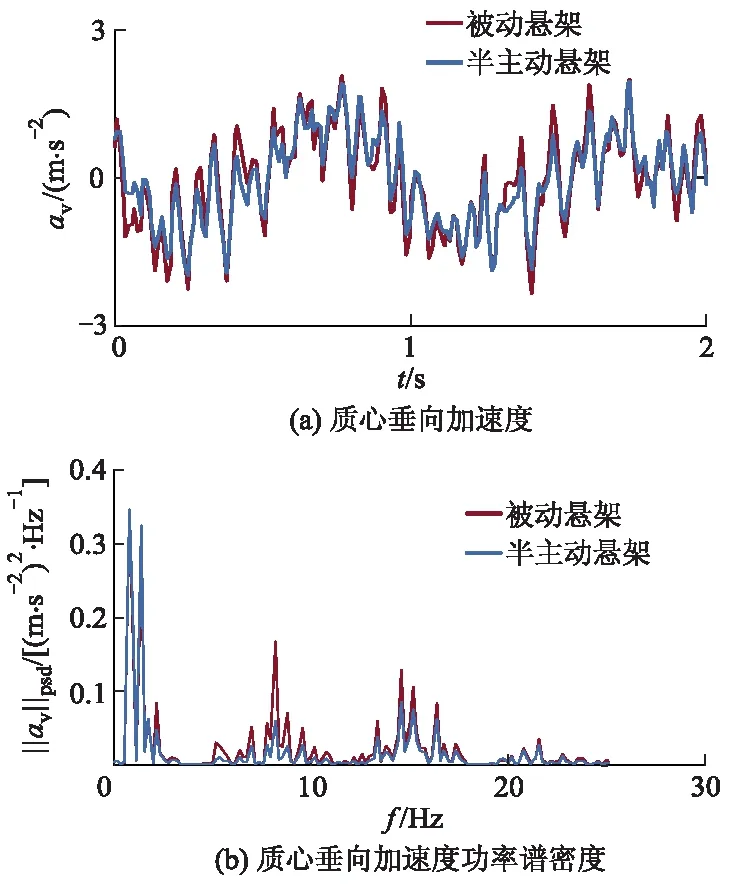
图9 质心垂向加速度仿真结果

f为频率；aφ为俯仰角加速度；aθ为侧倾角加速度；||·||psd为功率谱密度.

图10 俯仰角加速度仿真结果

图11 侧倾角加速度仿真结果

根据图9-11计算各性能指标均方根值，可以得到：相对于被动悬架，在所设计控制算法控制下的车身质心加速度、俯仰角加速度和侧倾角加速度均方根值分别降低了14.03%、18.26%和21.39%；在4.0～12.5 Hz人体敏感范围内和车身部分共振频率处三者的功率谱密度均得以显著降低.

俯仰角、侧倾角仿真结果分别如图12、13所示.

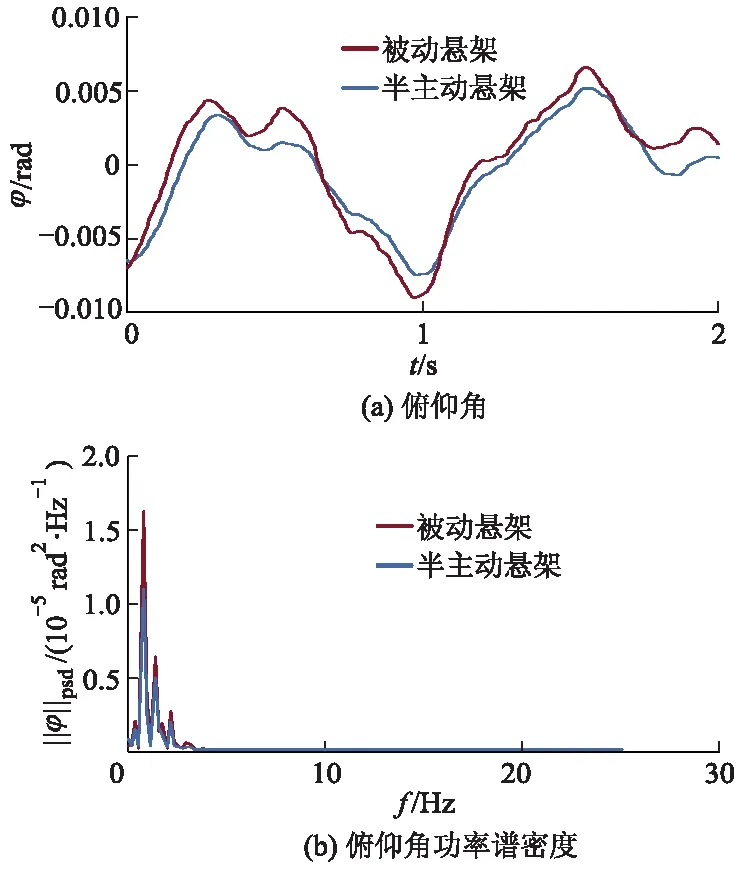
图12 俯仰角仿真结果

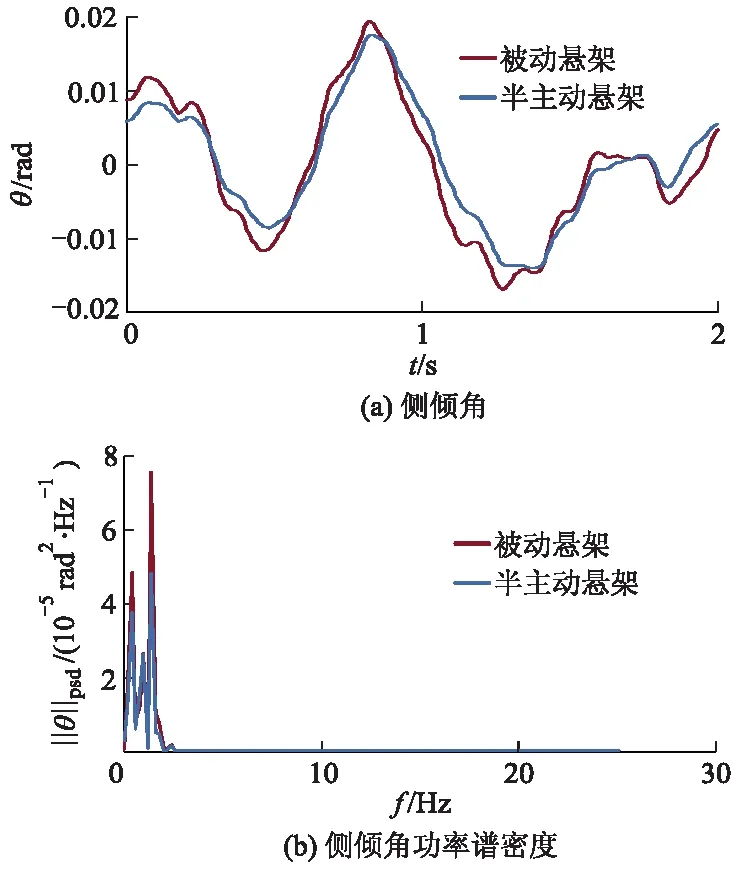
图13 侧倾角仿真结果

根据图12、13计算各性能指标均方根值，可以得到：较被动悬架，磁流变悬架的俯仰角和侧倾角的均方根值分别降低了15.40%和13.02%.从频域分析可知，在控制算法下，磁流变悬架的俯仰角功率谱密度以及侧倾角功率谱密度在车身部分共振处都有很大程度改善.

悬架动行程sf、轮胎动载荷Fr的仿真结果分别如图14、15所示.

图14 悬架动行程仿真结果

图15 轮胎动载荷仿真结果

从图14、15可以看出：相对于被动悬架，磁流变悬架的悬架动行程呈现一定程度的恶化(以左后悬为例)，但未超过4 cm，在乘用车设计要求的范围内；由于所设计的控制算法中垂向控制器采用了天棚控制方法，轮胎动载荷均方根值降低了9.79%(以左后悬为例)，相对较小，可以接受.

因此，所设计的磁流变悬架控制算法对于车辆舒适性提升效果明显，且对车身俯仰与侧倾有显著的抑制效果.

4 硬件在环试验及结果分析

为了验证所设计控制方法的有效性，利用HiL测试平台和D2p控制平台对所设计的控制方法进行硬件在环仿真试验，并将获得的控制效果与仿真控制效果进行对比分析，以验证控制算法的可行性.

4.1 硬件在环方案设计

硬件在环试验的方案如图16所示.其中ECU(electronic control unit)为电子控制单元.

图16 硬件在环试验方案

根据图16所示的试验方案，所设计的试验模型包括控制器模型和被控对象模型2部分，其中：控制器模型为设计的基于磁流变半主动悬架系统的车身姿态补偿Simulink控制算法模型；被控对象模型为整车动力学模型和磁流变减振器多项式模型.考虑到Carsim中整车仿真模型与HiL测试平台具有很好的兼容性，而Adams软件中整车多体动力学模型却无法做到，因此，根据整车性能参数建立Carsim整车仿真模型，以验证不同工况下整车控制效果，所设计的试验工况如图17所示.其中：vy为纵向速度；β为转向盘转角.

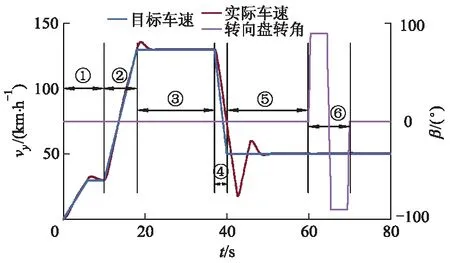
图17 试验工况

从图17可以看出：该试验工况主要分为6部分，选择C级路面作为系统外部输入，主要包括加速行驶、低速匀速行驶、百千米加速行驶、高速匀速行驶、紧急制动、蛇形转向等行驶工况，以验证控制算法对车身垂向振动、俯仰运动和侧倾运动的抵抗能力.

4.2 硬件在环试验结果分析

为利用上述工况进行硬件在环试验，将试验结果与仿真结果进行对比分析，以验证所设计控制算法的可行性.车辆在急加速工况、紧急制动工况、蛇形转向工况以及车辆以130 km·h-1匀速通过C级路面，硬件在环试验结果如图18、19所示.其中ab为车身垂向加速度.

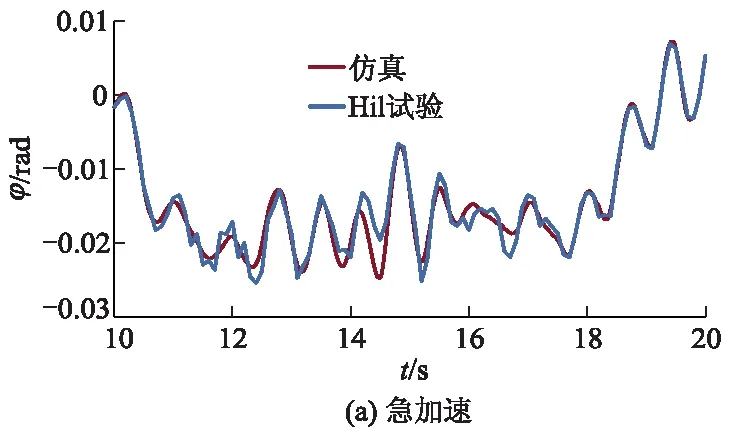
图18 急加速下的俯仰角和紧急制动俯仰角变化曲线

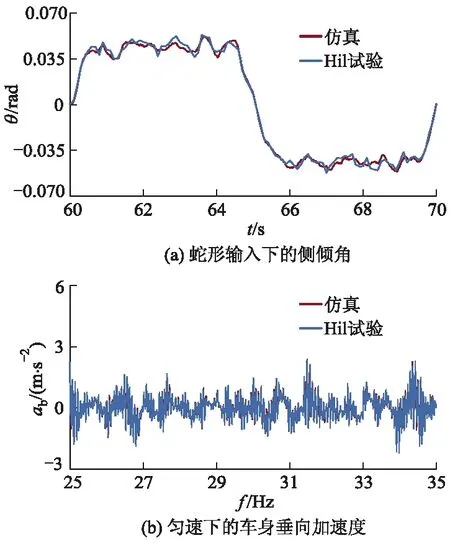
图19 蛇形输入下的侧倾角和匀速下的车身垂向加速度变化曲线

从图18、19可以看出：硬件在环试验结果与仿真结果具有一致性，两者误差很小，能够满足性能需求，进一步验证了所设计控制算法对车身姿态变化和车身垂向振动具有明显改善作用.

5 结 论

基于磁流变减振器外特性拟合得到的磁流变减振器多项式模型，可以很好地反映磁流变减振器工作时的滞回特性，便于磁流变半主动悬架的控制研究.将实际等效阻尼引入状态观测器设计方法中，实时更新观测器中悬架系统的参数矩阵，实现了对所需信号更为精确地估计.仿真分析和硬件在环试验结果表明：提出的控制算法对提高汽车乘坐舒适性和控制车辆行驶过程中的俯仰和侧倾都有较显著的改善效果.具体而言，在所提出的控制算法中，磁流变悬架的车身加速度、俯仰角加速度和侧倾角加速度均方根值分别降低了14.03%、18.26%和21.39%.说明所设计的控制算法可以显著优化车身姿态并有效改善车辆乘坐舒适性.