无人驾驶汽车平行泊车路径规划优化与跟踪
2022-09-05于蕾艳王显宇吴宝贵侯泽宇吴永辉
于蕾艳,王显宇,吴宝贵,侯泽宇,吴永辉
(中国石油大学(华东)机电工程学院,山东 青岛 266580)
应用于先进驾驶辅助系统(advanced driver assistance system,ADAS)的自动泊车技术一定程度上解决了“泊车难”问题.自动平行泊车关键技术包括路径规划方法和路径跟踪方法.在路径规划方法研究方面,路径规划类型包括多项式曲线、圆弧-直线、B样条曲线、Sigmoid函数和反正切函数曲线规划等.例如,直线—过渡曲线—圆弧段—过渡曲线—圆弧段五段式平行泊车路径规划满足曲率连续要求,路径跟踪难度较小[1];基于圆弧—直线组合曲线推导平行泊车可行泊车起始区域边界,对固定回旋曲线旋转和翻转变换得到曲率连续的平行泊车路径[2].在路径跟踪方法研究方面,采用纯跟踪算法、最优控制方法、改进迭代学习算法、模糊算法、线性反馈控制和滑模控制等[3].例如,基于非光滑控制的路径跟踪控制方法在有限时间内全局精确跟踪参考路径,具有抗扰动性和快速收敛性[4]的特点.但是,无人驾驶汽车路边平行泊车工况的泊车路径规划优化方法[5-6]、泊车路径跟踪方法还需深入研究,以综合提升路边平行泊车的各项性能.
笔者分析无人驾驶汽车路边平行泊车工况的特点,选取合理的多项式曲线进行路径规划.建立路径规划曲线参数优化设计数学模型,选取设计变量,分析泊车边界条件、路径曲率、避撞、泊车空间等要求,建立约束条件,选取合适的目标函数.采用粒子群优化算法得到路径参数泊车起始位置横坐标,再计算多项式待定系数,得到优化、平滑、曲率连续的规划路径曲线.基于纯跟踪算法进行泊车路径跟踪,通过Matlab平台仿真试验,验证泊车安全性、平稳性和乘坐舒适性的提升效果.
1 路边平行泊车工况描述
无人驾驶汽车路边平行泊车工况如图1所示,汽车1为路边待泊车位前方已泊汽车,汽车2为待泊的无人驾驶汽车,v为车速,bf为车位宽度,Ls为汽车2完成泊车后与前车1的安全距离,l为轴距,lf为前悬长度,lr为后悬长度,L为车长,b为车宽.泊车过程为汽车2的人机交互系统接收到乘车人泊车指令后,采用视觉传感器与超声波雷达融合方式实现车位检测.根据车位类型进行路径规划,基于线控底盘的运动控制单元控制车辆前轮转角与车速实现路径跟踪.以待泊车位的右前方角点为坐标原点,以车位纵向为x轴,建立直角坐标系.以汽车2后轴中点为参考点,A点为泊车起始位置,B点为泊车目标位置,汽车2沿泊车路径曲线AB驶入车位,完成泊车.

图1 路边平行泊车工况示意图
2 基于粒子群优化的泊车路径优化
2.1 泊车路径曲线类型和阶次选取
泊车路径规划采用多项式曲线.确定曲线阶次时,曲线AB光滑的要求如下:路径曲率连续要求路径曲线二阶连续;泊车过程中由于转向电动机转向性能约束和转向系统惯性特性,转向轮转角不能突变,要求路径曲线三阶连续,路径曲线阶次最低为四次,常采用奇次阶曲线.曲线阶次越高,待定系数越多,计算难度越大.因此,兼顾泊车曲线光滑、降低计算难度要求,采用五次多项式曲线.
在图1所示直角坐标系下,路径曲线表达式为
y=a0+a1x+a2x2+a3x3+a4x4+a5x5,
(1)
式中:y为汽车2后轴中点纵坐标值,m;x为汽车2后轴中点横坐标值,m;a0-a5为系数.
2.2 泊车路径的约束条件
设A点坐标为(xA,yA),B点坐标为(xB,yB).路径曲线在A、B两个端点处满足:
(2)
(3)
汽车准备泊车时与泊车完成时的车身姿态均与车道线平行,即泊车起始位置与泊车目标位置的车身航向角均为0,A、B点一阶导数均为0,即
(4)
(5)
在泊车起始位置A点,汽车未开始转向,转向轮转角为0,路径曲率为0,曲率为
(6)

由式(4)求导得A点处路径二阶导数为0,即
(7)
在泊车目标位置B点完成泊车,转向轮回正,转向轮转角为0,B点处路径曲率为0,可得
(8)
泊车路径的最大曲率κmax需要满足约束条件,确保路径可跟踪.约束条件如下:κmax对应的最小曲率半径1/κmax大于汽车最小转向半径Rmin,即
κmax<1/Rmin.
(9)
建立碰撞约束,为避免汽车与道路边缘碰撞,泊车过程中汽车右前顶点B′要始终在道路边缘左侧,由B′坐标计算公式得到约束条件为
(10)
由图1可知,B点横坐标xB由汽车2的轴距l、前悬长度lf及与前车1的安全距离Ls确定,即
xB=-(l+lf+Ls).
(11)
Ls取 0.5 m,代入式(11)中,求得xB=-3.705 m.根据GB/T 51328—2018《城市综合交通体系规划标准》,城市非机动车道宽度不小于2.5 m,泊车完成后,汽车2在泊车位中央,yB=bf/2=1.25 m,B点坐标确定.
假设汽车2靠道路右侧行驶,A点纵坐标简化计算为yA=bf+b/2.A点横坐标xA待优化.在yA确定的情况下,xA决定了路径长度,受限于汽车传感器探测范围,|xA|有上限值|xA|1.在满足泊车要求的前提下,|xA|越小,泊车所需空间越小.由图1可得xA的约束条件为
xA<-(l+lf+L+Ls).
(12)
泊车路径曲线中的未知量为xA、a0、a1、a2、a3、a4、a5.先优化得到xA,再通过6个等式约束方程(2)、(3)、(4)、(5)、(7)、(8)求解得到其他6个路径参数值.
2.3 目标函数
路径曲率影响泊车过程中的汽车平稳性,路径最大曲率κmax越小,跟踪路径所需转向轮转角就越小,泊车平稳性越好.xA影响路径长度,|xA|越小,泊车路径越短,泊车效率越高.|xA|与κmax存在矛盾,|xA|越大,κmax越小.设计目标函数时,权衡|xA|与κmax二者的大小.目标函数为
min(η1κmax+η2|xA|),
(13)
式中:η1和η2分别为κmax、|xA|的权重因子,由于κmax比|xA|小得多,取η1=63,η2=1.
综上,建立了包括式(13)所示的目标函数,式(2)、(3)、(4)、(5)、(7)、(8)所示的6个等式约束和式(9)、(10)、(12)所示的3个不等式约束,设计变量为xA的优化设计数学模型.
2.4 基于粒子群优化的路径参数优化
粒子群优化(particle swarm optimization,PSO)算法是一种精度高、收敛速度快、参数少、易实现的随机搜索算法,通过集体协作使群体达到最优.优化问题的每个潜在解视为搜索空间的一只鸟,称之为“粒子”.每个粒子有1个目标函数决定的适度值和1个速度来决定飞行距离和方向.所有粒子追随当前的最优粒子在解空间中进行搜索[7].参数选取如下:
1)粒子群规模N一般在[20,100]范围内取值,粒子群规模越大,越易找到全局最优解,但算法运行时间越长,取N=30个.
2)粒子维度D根据搜索空间维数取值,取D=1维.
3)以最小误差要求满足最大迭代次数M,取M= 50次.
4)学习因子c1和c2,c1影响局部最优值,c2影响全局最优值,取c1= 1.5,c2=2.5.
5)粒子最大速度vmax决定粒子飞行中可飞过的最大距离,vmax过大,粒子可能飞过最优解的位置;vmax过小,粒子陷入局部最优.vmax=λxdmax,λ∈[0,1],xdmax为粒子变化范围,取vmax= 0.3.
6)惯性权重w是PSO最重要的参数,调节粒子对解空间的搜索范围,增大w能提高全局搜索能力,减小w能提高局部搜索能力,合理的w是实现高效搜索和避免陷入局部最优的关键,择优选取w=0.5.
Matlab软件编程实现的PSO算法流程如图2所示,其中:pbest为粒子搜寻过的最优位置;gbest为整个粒子群搜寻过的最优位置.经9次迭代求解出最优值,目标函数值为20.743.泊车路径曲线起点横坐标xA=-14.955 m,满足路径最大曲率κmax=0.092 m-1小于汽车最小转向半径对应曲率的要求.确定xA值之后,求解式(2)、(3)、(4)、(5)、(7)、(8)组成的方程组,得到路径曲线参数值[a0,a1,a2,a3,a4,a5]=[0.091 7,-1.063 1,-0.358 0,-0.053 0,0.003 2,-0.000 07].PSO优化后的泊车路径五次多项式曲线表达式为

图2 PSO算法流程图
y=0.091 7-1.063 1x-0.358 0x2-
0.053 0x3-0.003 2x4-0.000 07x5.
(14)
基于PSO算法优化的泊车路径规划结果如图3所示.基于PSO算法优化的五次多项式泊车路径平滑且曲率连续,汽车一次性泊车入位,没有出现原地转向现象,减小了转向系统负荷.路径起始位置与目标位置曲率均为0,保证了汽车在路径端点转向轮回正.

图3 基于PSO算法优化的泊车路径规划结果
3 基于纯跟踪算法的泊车路径跟踪
纯跟踪(pure pursuit)算法是基于几何学的汽车横向控制方法[8],算法简单、易实现,在低速工况具有较好的跟踪效果.纯跟踪算法模型如图4所示,其中:P为预瞄点;ld为预瞄距离;R为汽车后轴中点转向半径;α为车身轴线与后轴中点A与预瞄点P连线的夹角;e为车身轴线与预瞄点的横向偏差;δ为前轮等效转角.

图4 纯跟踪算法模型
基于汽车后轴中点位置在目标路径上以预瞄距离长度匹配一个预瞄点,假设汽车后轴中点按照一定转向半径到达预瞄点,根据转向半径、预瞄距离及汽车坐标系下的预瞄角度确定前轮转角,实现对预瞄点跟踪.前轮等效转角控制律为
(15)
ld越大,控制效果越平滑,但会在某些急剧转角处产生转向不足情况;ld越小,控制效果越精确,但可造成汽车控制不稳定甚至震荡.将ld设为关于车速的函数,即
ld=gv+la,
(16)
式中:g为调节系数,取g=2;la为预设预瞄距离,m,取la=0.5 m;车速v=3 m·s-1.
路径起点设为(-14.955,3.330)m,泊车起始位置位于路径起点A,航向角为0.基于纯跟踪算法的路径跟踪结果如图5所示,汽车较准确地跟踪基于PSO算法优化的五次多项式曲线泊车规划路径.汽车在停止运动时的位置为(-3.949,1.249)m,规划的路径终点为(-3.705,1.250)m,位置误差|xe|= 0.243 9 m,|ye|= 0.001 5 m.汽车与道路边界最易碰撞处位于汽车右前顶点处,其纵坐标最小值为0.026 3 m,汽车运动时没有发生碰撞现象.路边平行泊车路径跟踪结果如图6所示,汽车前轮等效转角和航向角连续变化,保证了汽车泊车过程的平稳性与乘坐舒适性.从图6b可以看出:汽车运动过程中路径跟踪误差范围为[0,0.049 7]m,误差较小,汽车能较准确地跟踪规划路径.
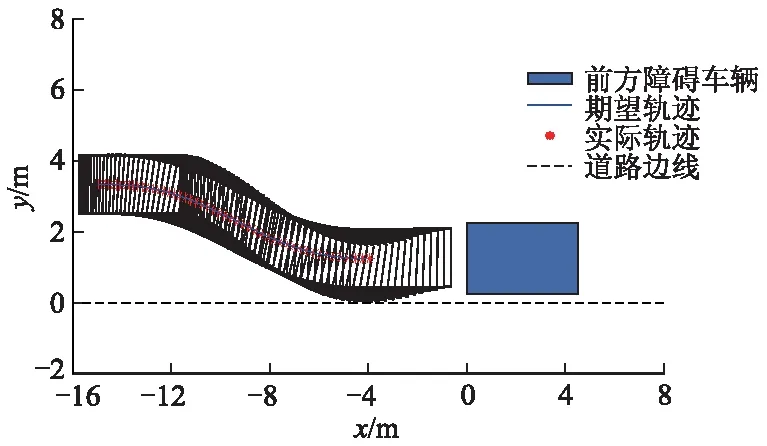
图5 路边平行泊车路径跟踪过程
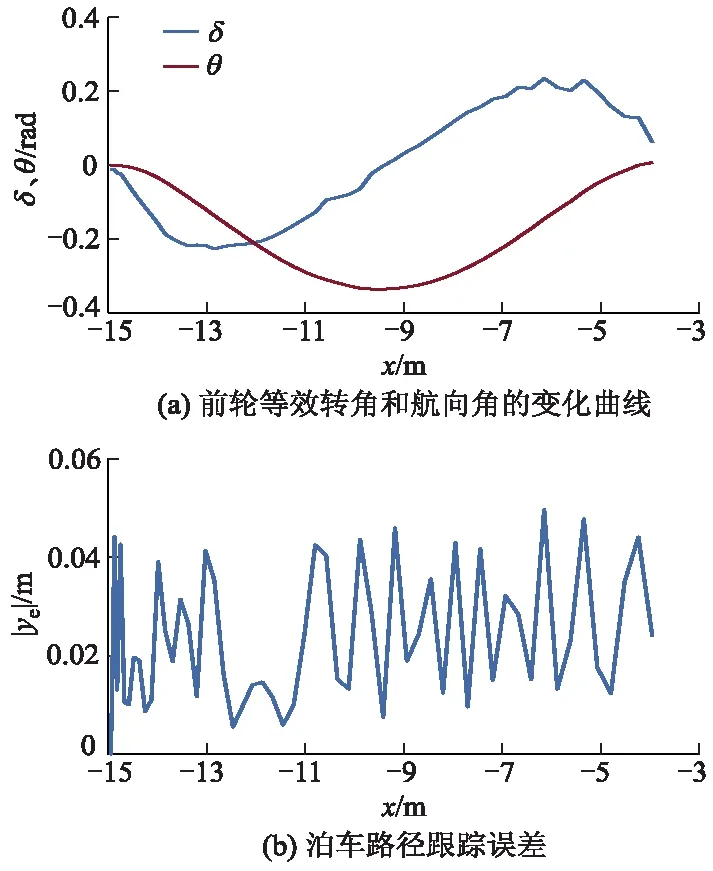
图6 路边平行泊车路径跟踪结果
4 结 论
1)基于粒子群优化算法的优化五次多项式曲线路边平行泊车工况路径规划方法,综合提高了泊车安全性、泊车效率、平稳性和乘坐舒适性等性能.设计变量取泊车起始位置横坐标,基于泊车边界条件建立6个路径曲线等式约束,基于路径曲率、避撞、减少泊车空间等要求建立3个不等式约束条件,选取最大曲率和泊车起始位置横坐标绝对值的加权和作为目标函数,建立路径规划曲线参数优化设计的数学模型方法科学合理.利用粒子群优化算法求解得到路径参数泊车起始位置横坐标,再计算路径曲线的6个多项式待定系数,获得了平滑、曲率连续的规划路径曲线.
2)无人驾驶汽车基于纯跟踪算法进行泊车路径跟踪,较精确地跟踪优化的五次多项式曲线路径,与周围障碍物无碰撞,满足安全性要求.前轮转角连续变化,满足泊车过程汽车平稳性及乘坐舒适性等要求.
