基于FCM的多无人机协同攻击决策建模方法
2022-09-05陈军梁晶程龙佟龑
陈军,梁晶,程龙,佟龑
1. 西北工业大学 电子信息学院,西安 710072 2. 空军工程大学 信息与导航学院,西安 710077
为谋求远超竞争对手的军事优势,克服高性能先进武器平台造价昂贵、研发周期过长等难题,美国国防高级研究计划局(DARPA)确立了“体系综合技术和试验(SOSITE)”项目,旨在通过体系的方法把包含武器、传感器和任务等系统的航空作战能力分布于大量可互操作的有人/无人平台上,促进最新技术在现有航空作战系统中快速且低成本地集成。目前,采用多架小型、低成本,传感器少但多用途的无人作战飞机组成编队,执行压制敌防空力量(SEAD)任务成为一种较为典型应用模式。
协同态势感知与决策作为“观察-判断-决策-行动(OODA)”任务回路的关键技术环节引起了国内外广泛的重视,其中,无人机编队在复杂不确定战场环境下,如何自主实施可解释的决策推理,提供合理的攻击决策方案对于增强指挥人员的决策优势,提升编队作战效能尤为重要。
目前,无人机攻击决策建模主要采用的是专家系统、影响图、贝叶斯网络、微分对策、强化学习、模糊规则等方法,一般可分为基于知识驱动和基于数据驱动2类。知识驱动的方法具备较强的解释性,决策推理简单高效,但准确度较低,适用于战场态势简单、熟悉,决策时效性要求较高的情况;数据驱动的方法具有较强的学习进化能力,但决策推理效率低,对数据的完备性和准确性要求高,适用于战场态势复杂、陌生,决策时效性要求适中的情况。
按照系统科学的观点,多无人机协同攻击决策系统可被认为是由多个自主系统构成的具有涌现特性的系统的系统(System of System,SoS),其协同关系复杂、约束条件众多、状态空间维数高,求解难度大,需要从体系的角度构建整体的决策建模框架。文献[11]基于多智能体强化学习算法,提出了基于执行-评判算法的集中式评判和分布式执行的算法结构,提升无人机的学习能力的同时保证了训练收敛,并且满足在线实时决策的需求。文献[12]提出了一种智能自组织算法(ISOA)。采用分布式控制体系结构,将全局优化问题分解为多个局部优化问题,帮助多无人机系统做出最优决策。文献[13]建立了多无人机博弈模型,提出了博弈支付函数,并引入态势矩阵来模拟战争信息的不确定性。文献[14]采用影响图分析法描述了多无人机协同空战机动决策过程,并建立决策模型,将多对多空战模型转换为一对一的版本。文献[15]将群决策理论应用于多无人机协同近距空战机动决策。首先确定机群中各决策点的决策偏好和决策效用权重,然后利用随机风险准则推测相应的敌方决策模式。文献[16]建立了不确定信息下无人机模糊态势模型,并提出了一种异步一致性拍卖算法用于解决此种态势模型下的空战决策问题。
近些年来,将认知科学、人工智能应用于无人系统的决策问题研究成为重要趋势。其中,模糊认知图(Fuzzy Cognitive Map,FCM)是一种可用于建模和模拟动态系统知识表示和因果推理,为作战任务提供决策支持的有效工具。
因此,本文将借鉴人的决策心智模式,设计包含感性和理性2条实施路线的决策机制,采用智能体模糊认知图(Agent-Based Fuzzy Cognitive Map,ABFCM)建立多无人机协同攻击决策系统模型框架,采用模糊灰色认知图(Fuzzy Grey Cognitive Map,FGCM)建立多无人机协同态势感知模型与攻击决策模型,并通过引入直觉模糊集提高决策输出阈值选取的客观性。同时,为减少对专家知识的依赖,采用动量梯度下降学习算法提高模型的学习进化能力。
1 多无人机协同攻击决策系统模型
1.1 模糊认知图及其扩展模型
经典的FCM模型由概念节点、有向弧及其关联权值矩阵组成。节点表示系统的属性、特征、性能等;有向弧表示节点间的影响关系,影响程度由关联权值矩阵描述,整个FCM通过各概念之间的因果关系以及相互作用来模拟复杂系统行为。FCM能将输入映射为输出的收敛状态:固定点或极限环,也可能终止于“混沌”发散状态。由于FCM建模方法简单、灵活以及在不同应用场景良好的适应性和易用性,衍生出了许多扩展模型。其中,ABFCM模型的每个节点可以是不同的智能体(Agent),拥有各自的推理算法,通过消息传递机制(Message)与其他节点相互作用,当每个节点算法一致时,又将回归到经典的FCM,适用于分布式决策系统的建模,如图1所示。
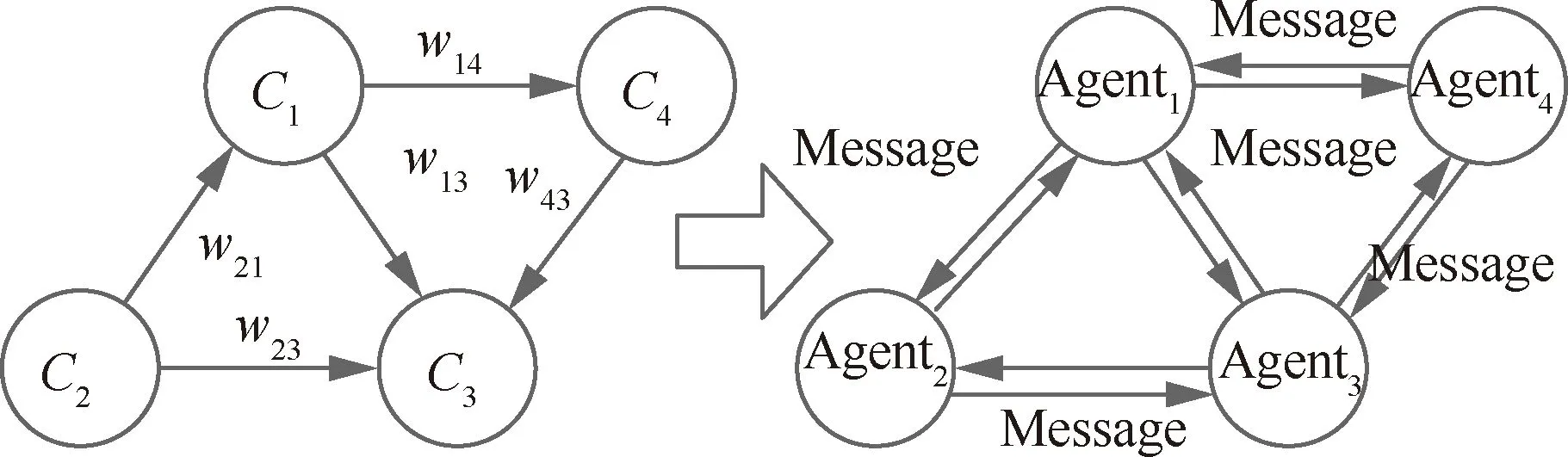
图1 经典FCM与ABFCM的映射关系Fig.1 Mapping between classical FCM and ABFCM
式(1)为经典FCM节点状态推理模型:
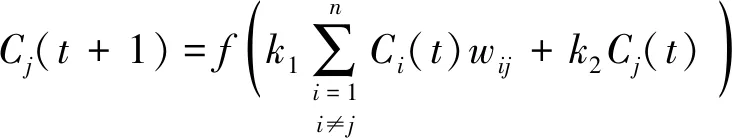
(1)
式中:()、()分别表示时刻原因节点和结果节点的状态值;为第个概念节点对第个概念节点的因果关联权值;为系统中概念节点的总个数;,∈[0,1],分别表示原因节点综合影响和节点自身状态所占的比重。表示概念节点的激活函数,具有多种表达形式。
ABFCM是将经典FCM中的节点映射为智能体,其节点状态的推理方程由式(1)变换成式(2)的形式:

,…,)
(2)

相比于经典FCM、FGCM的节点和权值均用灰数来表示,可充分表达系统模型的不确定性特征,如图2所示。
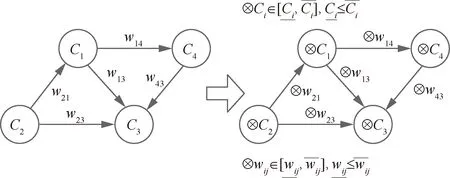
图2 经典FCM与FGCM关系示意图Fig.2 Mapping between classical FCM and FGCM
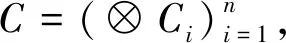
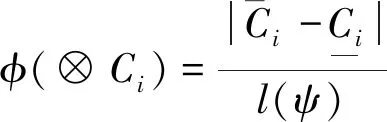
(3)
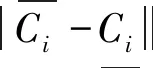

(4)
FGCM的节点状态值推理公式为
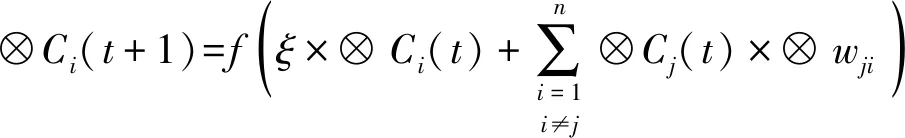
(5)
式中:表示节点前一时刻状态值对当前状态值的影响,取值范围为[0,1]。
激活(·)主要有sigmoid型和tanh型,分别对应节点状态值属于[0,1]和[-1,1]这2种情况。

(6)

(7)
式中:为参数,取值越大,激活函数越陡峭。
其中,灰数的加法、乘法运算法则为
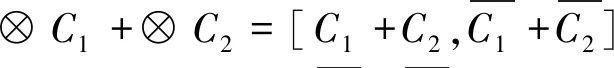
(8)
⊗×⊗=

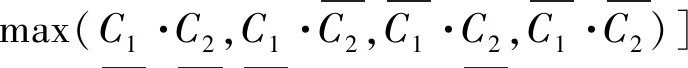
(9)
将灰数转化为准确值的操作过程称为白化(Whitenization),白化的一般公式为

(10)
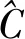
1.2 基于ABFCM的协同攻击决策系统模型
将不同类型的无人机按照SoS的角度进行任务功能集成,可以建立基于ABFCM的多无人机协同攻击决策系统模型框架,它包含态势感知和攻击决策2个部分,如图3所示。
态势感知部分主要由目标识别与状态估计Agent、意图预测与威胁估计Agent、攻击任务安全性估计Agent和攻击效果估计Agent组成。各个功能的Agent在多无人机通信组网的支持下,按照ABFCM 的消息机制协同工作。
在攻击决策部分,主要由基于杏仁核决策的感性攻击决策推理Agent和基于直觉模糊集的理性攻击决策推理Agent组成。感性攻击决策主要针对敌我态势简单且有历史决策案例支持下的快速决策推理;理性攻击决策主要针对敌我态势复杂且缺乏专家知识支持下的因果决策推理。
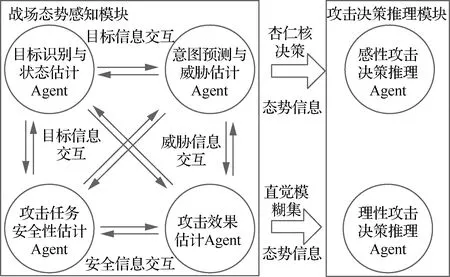
图3 基于ABFCM的协同攻击决策系统模型框架Fig.3 Model framework of cooperative attack decision system based on ABFCM
2 多无人机战场态势感知建模
战场态势感知模块的主要任务是基于环境、目标和无人机编队的数据和信息进行综合与处理,形成对态势的理解和预测,为攻击决策推理提供信息支持。考虑到战场环境的对抗性,利用FGCM在不确定性表达和推理上的模型特点,分别建立各个功能Agent的因果推理模型。
2.1 目标识别与状态估计Agent的FGCM模型
如图4为目标状态识别与状态估计FGCM模型,表1为模型概念节点定义。

图4 基于FGCM的目标识别与状态估计因果推理模型Fig.4 Causal reasoning model for target recognition and state estimation based on FGCM
参照FGCM模型方法,对于⊗、⊗、⊗这类可直接由传感器测量得到的节点,只需根据数据的最大、最小值将其进行灰数形式表达即可。目标类型⊗为综合防空系统,一般包括:地面防空雷达、指挥通信所、导弹发射车。目标载荷类型⊗一般包括:雷达、导弹、通信电台。对于目标载荷状态⊗,雷达工作状态主要包括:搜素、跟踪、制导、静默;导弹工作状态主要包括:未发射、瞄准、发射;通信电台工作状态主要包括:未工作、间歇工作、正常工作。基于节点⊗和⊗的状态信息,目标识别与状态估计Agent采用数据结构化封装的形式,将模型推理得到的目标状态节点(⊗)信息通过ABFCM的消息传递机制与态势感知模块中的其他Agent进行信息交互。

表1 目标识别与状态估计FGCM模型节点定义
2.2 意图预测与威胁估计Agent的FGCM模型
如图5为意图预测与威胁估计FGCM模型,表2为模型概念节点定义。

图5 基于FGCM的意图预测与威胁估计因果推理模型Fig.5 Causal reasoning model for intention prediction and threat estimation based on FGCM
意图预测与威胁估计FGCM模型中,输入节点状态值的量化规则如下:
由于雷达的工作过程为先搜索后跟踪,节点⊗的评估为雷达搜索能力与跟踪能力的并联综合,两者的具体计算方法见文献[25]。

表2 意图预测与威胁估计FGCM模型节点定义
⊗=·
(11)
目标机动性能⊗是指目标采取一系列机动动作来改变相对态势的能力,由操作效能系数以及机动参数来进行量化,与的具体计算方法见文献[26]。
⊗=(·)
(12)
目标干扰压制能力⊗是指敌方干扰设备干扰我方通信与电子设备的作战效能的能力,影响因素较多,不做详细赘述,参考文献[27]。
目标火力打击能力⊗是指敌方可对我方造成的最大毁伤程度。表示第种类型武器的命中概率,为第种武器的数量,为武器类型总数。

(13)
目标载荷状态⊗量化规则为:雷达{静默:0.1,搜索:0.3,跟踪:0.6,制导:0.9},导弹{未发射:0.1,瞄准:0.5,发射:0.9},通信电台{未工作:0.1,间歇:0.5;正常:0.8}。
目标位置优势⊗的评估为角度优势、距离优势、高度优势的综合,、以及的计算方法参考文献[28]。
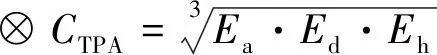
(14)
目标运动优势⊗即目标当前速度对位置的改变能力。其中,为我方速度,为敌方目标速度,为我方最佳速度。

(15)
目标协同优势⊗包括了目标与其他敌方战场实体之间信息的通信能力和实体之间相互协同工作的能力。
⊗=(·)
(16)
数据链的通信能力评估方法参考文献[29],目标之间的协同能力的计算公式为

(17)
式中:为同类目标对任务过程的辅助度;表示异类目标对任务的辅助度;,分别为同类目标和异类目标的数量。
经过模型因果推理可得到目标意图的短暂预测和当前威胁的估计。同样,模型输出节点(⊗)的信息可以通过消息机制传递,支持攻击决策Agent模型的因果推理工作。
2.3 攻击任务安全性估计Agent的FGCM模型
如图6所示为攻击任务安全性估计FGCM模型,表3为模型概念节点定义。

图6 基于FGCM的攻击任务安全性估计因果推理模型Fig.6 Causal reasoning model of attack task security estimation based on FGCM
攻击任务安全性估计FGCM模型的输入节点主要是战场态势信息,具体量化规则如下:
对于无人机来说,自然环境状态⊗主要考虑地形状态Te和大气环境状态At的影响。
⊗=(·Te+·At)
(18)
式中:和为影响系数,地形状态Te的量化规则为:{山地:0.9,高原:0.7,丘陵:0.5,盆地:0.3,平原:0.1}。大气环境状态At的归一化公式为

表3 攻击任务安全性估计FGCM模型节点定义
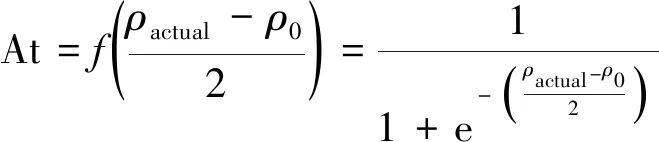
(19)
式中:为标准大气密度;为飞机所在海拔的实际大气密度。
电磁环境状态⊗的评估为频谱占用度,时间占有度,相对功率强度EP的综合。
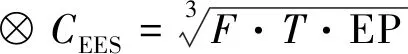
(20)
我方无人机生存状态⊗的评估函数如下,其中表示被击毁或锁定的无人机数量。
⊗=08-02
(21)
对抗措施⊗分为软对抗和硬对抗措施,量化规则为:{均完备:1,缺少软对抗措施:0.7,缺少硬对抗措施:0.5,无对抗措施:0}。
数据通信能力⊗与单位时间内传递的信息量、节点数、传输速率有关,同2.2节的。
攻击任务安全性估计Agent同时接收意图预测与威胁估计Agent传递的目标威胁程度节点(⊗)信息,经过模型因果推理得到攻击任务安全程度节点(⊗)状态值,用于支持攻击决策Agent模型的因果推理工作。
2.4 攻击效果估计Agent的FGCM模型
如图7为攻击效果估计FGCM模型,表4为模型概念节点定义。

图7 基于FGCM的攻击效果估计因果推理模型Fig.7 Causal inference model of attack effect estimation based on FGCM

表4 攻击效果估计FGCM模型节点定义Table 4 Meaning of node of attack effect estimation model
攻击效果估计FGCM模型中的输入节点状态值的确定主要基于态势感知模块中的其他Agent提供的信息。目标战术协同能力⊗由协同探测能力、协同防御能力、电子对抗能力以及指挥控制角色等因素来综合评估。协同探测能力、协同防御能力与目标在综合防空系统中的部署位置有关。目标军事与战术价值⊗、电子对抗能力以及指挥控制角色与目标类型有关,具体量化值如表5所示。

表5 目标类型与部分节点状态对应表
目标防御对抗能力⊗是指导弹发射车的防空能力,表示第个目标可对我方的拦截次数,max为拦截次数的最大值。
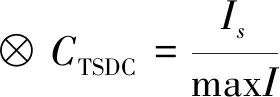
(22)
最后,经过模型因果推理得到攻击效果节点(⊗)状态值,用于支持攻击决策Agent模型的因果推理工作。
3 多无人机协同攻击决策建模
3.1 感性攻击决策Agent的杏仁核模板匹配模型
借鉴人脑杏仁核对外部刺激的快速应激反应机理,可以采用基于态势-决策模板快速匹配的方法构建感性攻击决策推理模型。
假设典型的决策条件下,可将输入节点状态值与决策节点状态值存储,如式(23)所示:
=[⊗,⊗,…,⊗:⊗+1]
(23)
式中:为存储的态势-决策模板数据;为模板中输入节点的总个数;⊗,⊗,…,⊗为输入节点的状态值,⊗+1为决策节点的状态值。当出现新的态势时,可以快速与态势-决策模板库进行匹配度计算,如式(24)所示:


(24)

3.2 理性攻击决策Agent的FGCM模型
理性攻击决策模式适用于敌我战场态势信息非典型,知识经验支持不足,决策时效性要求适中,推理模型可解释等应用场景。如图8所示为基于FGCM的理性攻击决策因果推理模型,表6为模型中各概念节点的定义。
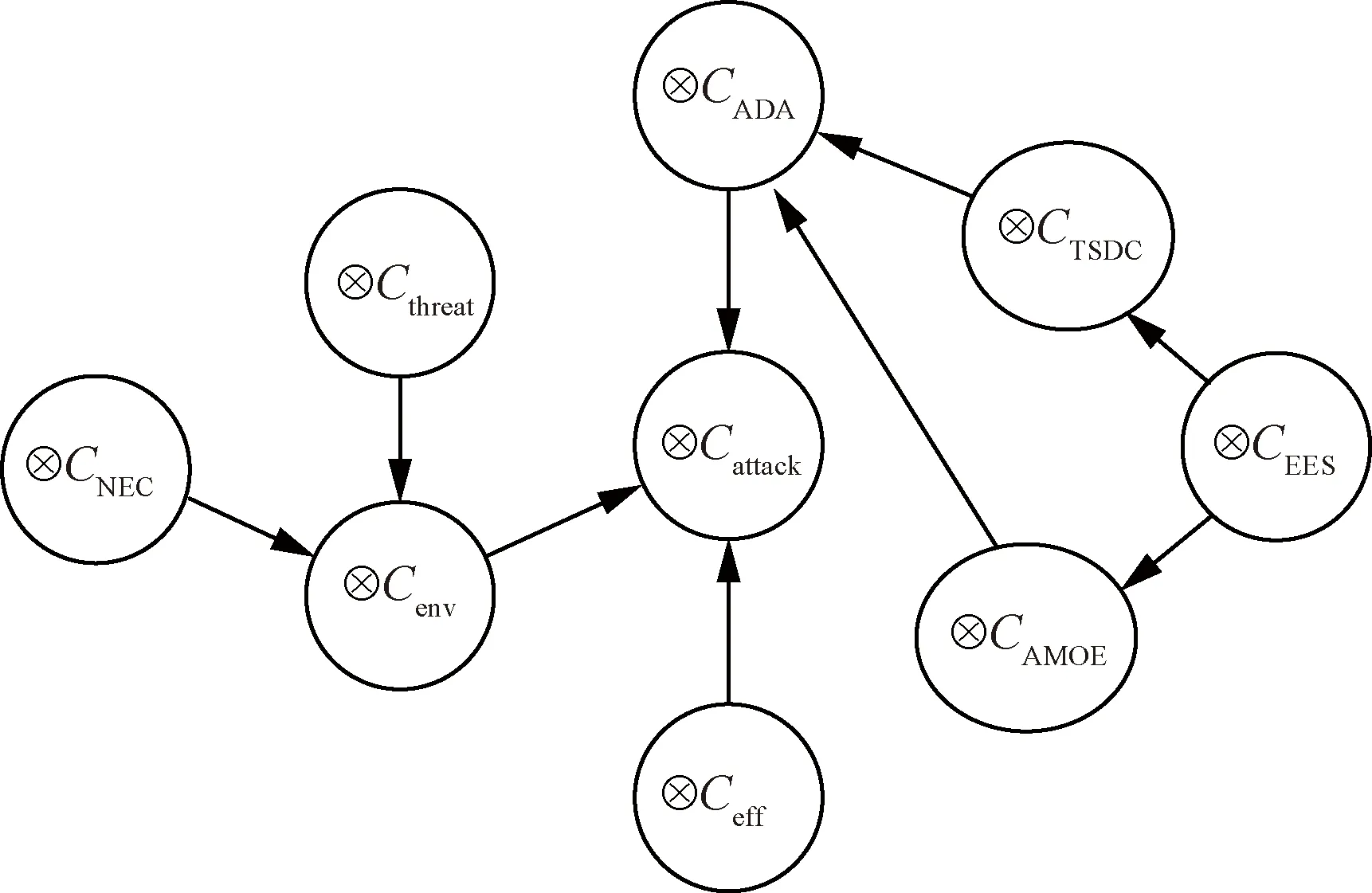
图8 基于FGCM的理性攻击决策因果推理模型Fig.8 Causal reasoning model of rational attack decision based on FGCM

表6 理性攻击决策FGCM模型节点定义Table 6 Meaning of node of rational attack decision model
理性攻击决策FGCM模型的输入节点状态⊗、⊗、⊗由态势感知模块中的各个Agent经过推理得到,节点⊗、⊗、⊗已在态势感知部分进行解释,不再重复。
攻击导弹作战效能⊗的评估采用WSEIAC(Weapons System Effectiveness Industcy Advisory Committee)模型方法,将系统效能解析为相互独立的3个部分:可用性′、可信性′和能力′。
⊗=(′·′·′)
(25)

(26)
式中:MTBF表示系统可靠性,与武器系统可靠度、导弹战备值班可靠度等相关;MTTR为维修性,与武器控制系统有关。
′=××
(27)
式中:为可靠性,为目标识别与导引能力,为导弹的抗干扰能力。

(28)
式中:为归一化后的武器装备能力因子,共个,为第个能力因子对应的权值。
攻击毁伤能力⊗由导弹命中概率和毁伤能力2部分确定。表示导弹命中距目标第处位置时的毁伤能力,为命中第处的概率,为导弹有效毁伤范围。

(29)


图9 理性攻击决策阈值的示意图Fig.9 Description of rational attack decision threshold
3.3 基于直觉模糊集的理性攻击决策阈值算法
3.3.1 直觉模糊集
设论域是一个非空集合,则上的直觉模糊集可以表示为

(30)
式中:()和()分别为论域中元素属于的隶属度和非隶属度,即:
():→[0,1],∈|→()∈[0,1]
(31)
():→[0,1],∈|→()∈[0,1]
(32)
同时满足∈, 0≤()+()≤1,则有
()=1-()-()
(33)
式中:()为元素属于的犹豫度,用来描述元素是否属于集合的不确定程度。对于任意的,有0≤()≤1。
3.3.2 损失函数



表7 损失函数Table 7 Loss function

3.3.3 攻击决策阈值计算方法
根据攻击决策模型推理节点状态表构建一个×直觉模糊决策矩阵,为攻击决策模型节点个数,为攻击决策模型推理迭代次数。矩阵组成元素为(,),其中隶属度为第个节点第次迭代推理后的状态白化值,选定一个犹豫度后,按照公式=1--计算得到非隶属度。
将评估指标分为2类:成本性指标和效益型指标,分别构建损失函数矩阵。
效益型损失函数矩阵:
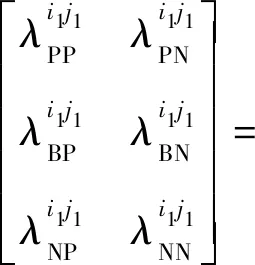

(34)
成本型损失函数矩阵:
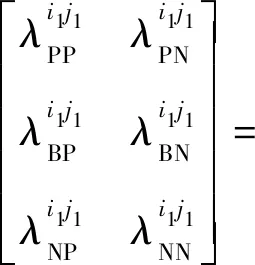

(35)
式中:为自适应风险规避系数,公式为
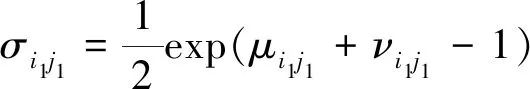
(36)
式中:0≤≤05,与犹豫度有关,犹豫度越低,的值就越高,表明对目标信息的获取越准确,获得更充足的目标信息,分类越精确。
由于不同时刻的状态值对攻击决策的影响是不同的,越接近于当前时刻对决策结果的影响越大,因此需要对不同时刻进行时间序列赋权,采用逆泊松分布法确定不同时间点的时间序列权值,得到动态融合后的损失函数矩阵。
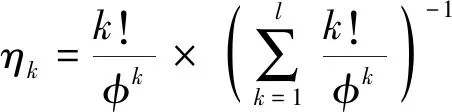
(37)

基于贝叶斯最小风险理论求得该目标对应的决策阈值:

(38)

(39)
3.4 基于MGD的理性攻击决策模型学习算法
为了减少理性攻击决策FGCM模型对专家知识的依赖,采用学习算法来提高模型对数据样本的参数学习能力具有较好的应用前景。常用的FCM模型学习算法有:① Hebbain非监督学习算法,学习速度快、精度低;② 种群学习算法,学习精度高、学习速度慢。本文采用基于动量梯度下降(MGD)的学习算法以求同时兼顾模型的学习精度和速度。
梯度下降算法的基本原理如下:
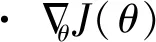
(40)
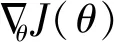
常用目标函数为均方误差损失函数。
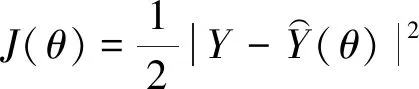
(41)

对于存在多个极值的误差函数,梯度下降算法易陷入局部最优,因而引入梯度动量来克服。
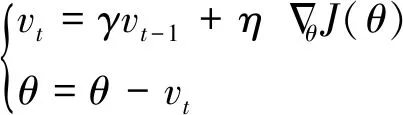
(42)
式中:为时刻梯度的动量,为权重因子。

① 初始节点间不存在因果关系时,在学习后也不存在。即

(43)
② 初始节点之间存在因果关系时,在学习后因果关系的正负符号不变。即
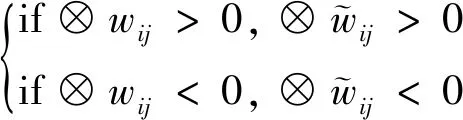
(44)
③ 学习过程中,每次迭代都需保持模糊权值的下界应小于等于上界。即

(45)
基于MGD的FGCM学习算法实施步骤为:
按照表6顺序获取模型样本数据。
由专家确定模型的初始关联权值矩阵。

设计模型学习误差损失函数。
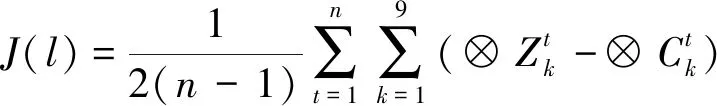
(46)
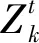
采用反向传播算法,权值变化量为
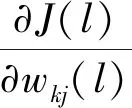
(47)
式中:Δ()为权值的变化量,ϑ为学习率。当采用sigmoid函数作为激活函数时,对于任意连接权值⊗,其更新量为

(48)
其中:为动量学习率。
每个权值的更新迭代计算公式如下:
()=(-1)+Δ()
(49)
经过不断迭代学习,满足以下条件时,终止学习。
()≤error or≥max_iter
(50)
式中:error为学习算法可允许的最大误差,max_iter为最大可迭代次数。
4 案例仿真与分析
以4架无人机组成异构无人机集群执行SEAD(Suppression of Enemy Air Defense)任务为场景,开展协同攻击决策模型和算法的案例仿真与分析,如图10所示。我方无人机主要包括无人侦察飞机、无人机电子战飞机和无人攻击机等,敌方目标主要是指综合防空系统(Integrated Air Defense System,IADS),其中包括防空雷达车、指挥通信所、防空导弹车等类型的目标。由于目标具有较强的综合对抗能力,且我方无人机由于功能和分工不同,需要在编队通信组网的支持下协同完成战场态势感知和协同攻击决策任务。
案例仿真与分析主要包括4个方面的内容:① 态势感知模块仿真与分析,主要验证Agent模型推理的有效性;② 理性攻击决策模型仿真与分析,重点验证基于直觉模糊集的决策阈值算法的有效性;③ 基于MGD的理性攻击决策模型仿真与分析,对比不同学习算法在模型应用中的性能差异;④ 感性攻击决策模型仿真分析,验证态势-决策模板快速匹配的有效性。

图10 基于SEAD任务的多无人机协同攻击决策示意图Fig.10 Schematic diagram of multi-UAV cooperative attack decision-making based on SEAD mission
4.1 多无人机态势感知模块仿真与分析
由于目标识别和状态估计的FGCM模型一般采用基于模糊规则库的因果推理方法。该方法应用较为广泛,技术相对成熟,且仿真想定已明确敌方目标为综合防空系统,故在此不再详述。
1) 意图预测与威胁估计Agent的仿真与分析
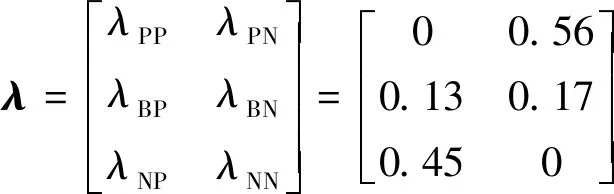
考虑到专家知识的主观性,意图预测与威胁估计FGCM模型的初始灰数权值矩阵为

模型各概念节点的初始状态值以及因果推理后的状态值如表8所示。

表8 意图预测与威胁估计FGCM模型仿真结果
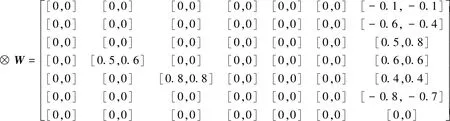
模型各概念节点的初始状态值以及因果推理后的状态值如表9所示。

表9 攻击任务安全性估计FGCM模型仿真结果
3) 攻击效果估计Agent的仿真与分析
模型的初始灰数权值矩阵为

模型各概念节点的初始状态值以及因果推理后的状态值如表10所示。
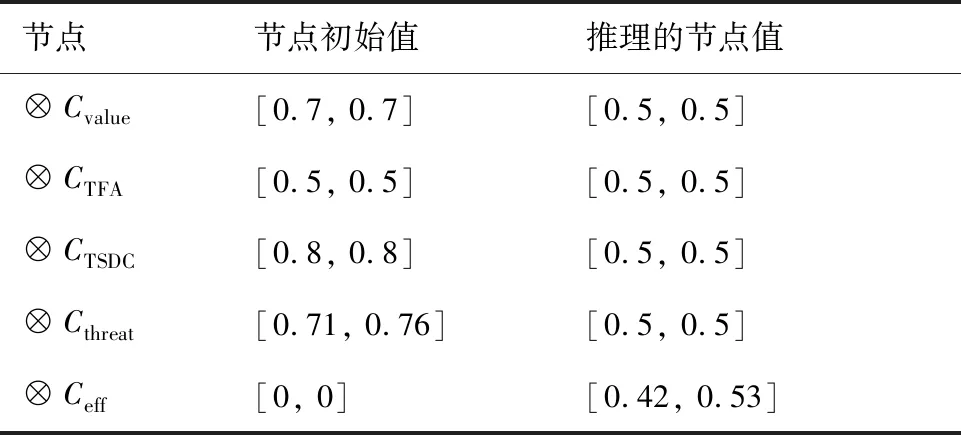
表10 攻击效果估计FGCM模型仿真结果
通过对态势感知模块各个Agent的仿真,假定目标是处于瞄准状态的导弹发射车,意图预测与威胁估计Agent输出的目标威胁度为[0.71,0.76],攻击任务安全性估计Agent输出的攻击任务安全度为[0.61,0.72],攻击效果估计Agent输出的攻击效果为[0.42,0.53],各Agent 仿真推理结果与信息传递关系如图11所示。
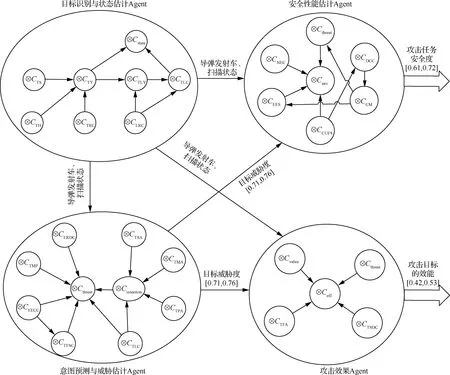
图11 多无人机态势感知模块仿真过程与结果Fig.11 Simulation process and results of multi-UAV situation awareness module
4.2 理性攻击决策模型仿真与分析
在多无人机态势感知的基础上,对理性攻击决策模型进行仿真与分析。
基于专家知识设定节点初始权值矩阵,激活函数为sigmoid型,推理节点状态如表11所示。
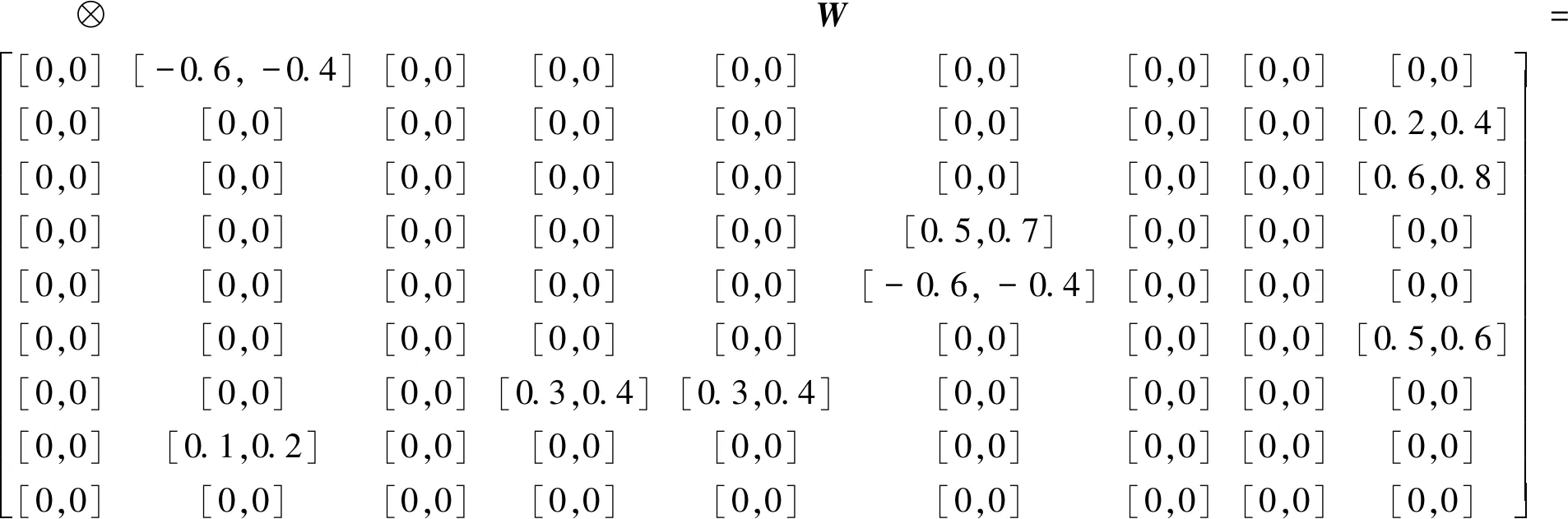

表11 攻击决策FGCM模型仿真结果
推理结果分析:当目标威胁度较高,电磁环境和自然环境较好,但敌方防御能力较强时,得到的推理决策结果值为[0.64, 0.72]。
根据3.3节攻击决策阈值计算方法,此时的直觉模糊决策矩阵如下:
=

将8个评估指标节点分为成本型指标{⊗,⊗}和效益型指标{⊗,⊗, ⊗,⊗,⊗,⊗},分别根据式(34) 和式(35)求得各自的损失函数矩阵。
由权值矩阵和不同时刻的时间序列权值=[0200 0,0266 7,0533 3]得到目标属性的综合权重,动态融合后得出此时损失函数矩阵如下:
根据式(38)和式(39)求得和分别为0.35和0.75,此时决策函数为

(51)
推理结果显示,当前的决策结果为不确定,需要继续观察分析。进一步推理后,对攻击决策的未来状态进行分析,发现由于⊗、⊗、⊗、⊗、⊗这些间接影响决策结果节点消息的传递成功,决策节点的状态值为[0.78,0.84],白化后节点值为0.81。此时的决策结果为攻击目标。
按照上述仿真流程,假设2组不同战场态势下输入初始节点状态分别为

[03,04],[07,08],[04,04],
[03,04],[03,04],[0,0]]
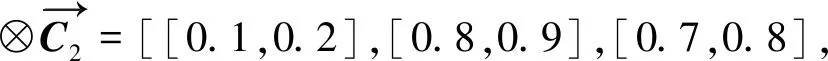
[06,07],[01,02],[06,07],
[06,07],[05,06],[0,0]]
对于2个案例初步定性分析可知,案例1目标威胁度高,环境安全性差,且敌方防御能力较强,电磁环境和自然环境状态一般,从而不利于攻击;案例2目标威胁度低,环境安全性好,且敌方防御能力较差,电磁环境和自然环境状态好,此时的决策结果应为攻击。
将上述2组初始节点状态分别输入攻击决策FGCM模型,案例1因果推理后得到的输出状态节点状态值为[0.38,0.46],白化后节点状态值为0.42,此时决策阈值和分别为0.53和0.81,即推理输出结果为规避目标。案例2因果推理后得到的输出状态节点状态值为[0.76,0.82],白化后节点状态值为0.79,此时决策阈值分别为0.36和0.68,即推理输出结果为攻击目标。因此,2组决策推理输出与案例初步定性分析结果吻合。
4.3 基于MGD的理性攻击决策模型仿真分析
为了便于验证所提出的动量梯度下降学习算法在FCM理论模型学习中的可行性,将4.2小节中节点权值矩阵、初始节点状态以及各时刻的推理状态值作为学习样本数据。使用FCM模型常用的赫布学习算法(Hebbian)、遗传算法(GA)以及本文提出的动量梯度下降(MGD)学习算法,基于初始参数和统一迭代终止条件:(误差error≤0.005,最大迭代次数max_iter=500)计算各学习算法的终止误差和耗时,学习算法效果如表12所示,误差曲线如图12所示。

表12 学习算法效果对比表Table 12 Comparison of effects of learning algorithms

图12 学习算法误差曲线图Fig.12 Error curves of learning algorithms
表12中可以看出,Hebbian算法在经过迭代后,算法快速满足了最大迭代次数终止条件,计算得到的平均学习误差为0.067,在所有算法中最大,但算法耗时最短为4.324 82 s。GA算法的学习精度为0.014,结合图12,虽然在迭代200次后GA算法的误差值已趋于稳定,但由于不满足迭代终止条件error≤0.005,所以在满足最大迭代次数后,算法终止,整个过程花费时间268.850 87 s。MGD算法的误差值可以在较短的时间内快速收敛,在计算到误差值为0.002 38时,算法耗时23.993 22 s。因此可以看出所提出的MGD学习算法相较于Hebbian算法,虽耗时长,但精度有大的提升;而相较于GA算法,耗时方面有大的改进,精确性和收敛性得到兼顾。
为了进一步验证各学习算法的性能,考虑到专家知识可能受各种因素影响,在原有灰数权值的基础上,将其上下限区间增大1倍和缩小1倍,形成3种不同灰度权值下的学习样本数据,使用上述3种学习算法进行训练,分别得到各自的误差曲线,如图13所示。
从图13可以看出,随着权值灰度的减小,Hebbian算法和MGD算法的学习误差值也在减小,而GA算法的表现没有太大差别。图13(a)中,在使用Hebbian学习算法进行训练时,权值灰度增大1倍,误差曲线位置明显升高,而缩小1倍的误差曲线与基准误差曲线差异较小,说明Hebbian学习算法对于权值灰度变化的敏感性不稳定;图13(b)中,3条误差曲线差异较小,且相对位置关系发生变化,说明GA算法对于权值灰度变化的敏感性较差;图13(c)中,不同权值灰数下,MGD算法均能在较短的时间内快速收敛,并且随着权值灰数的减小,学习误差值也在减小,说明MGD算法在不同权值灰度条件下的收敛性和敏感性均有较好表现。
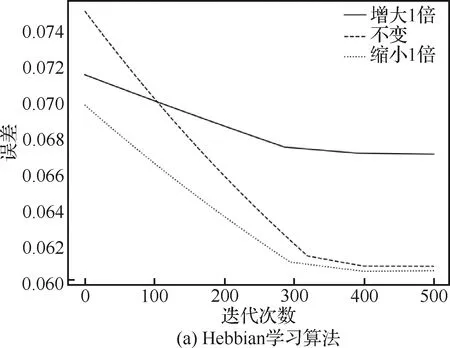
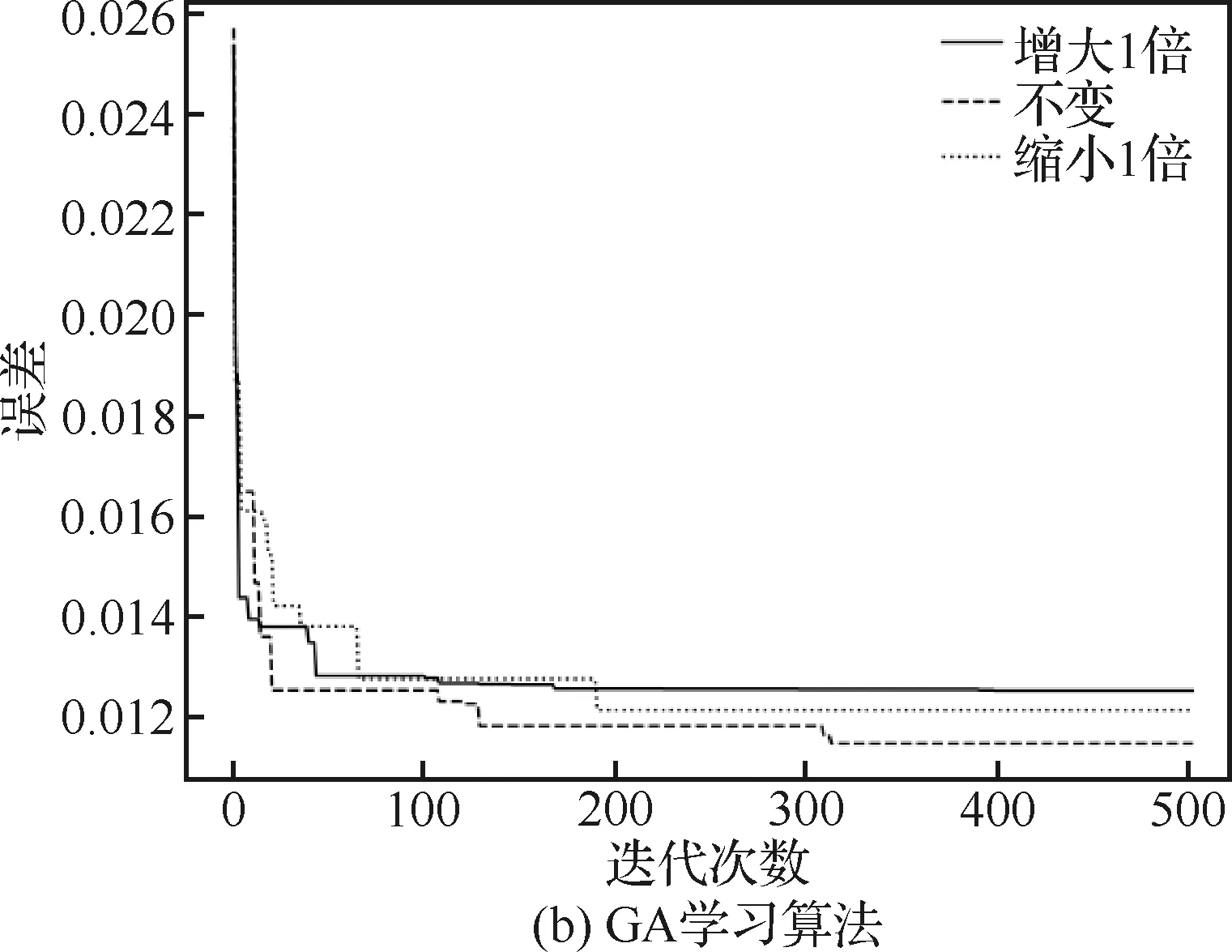
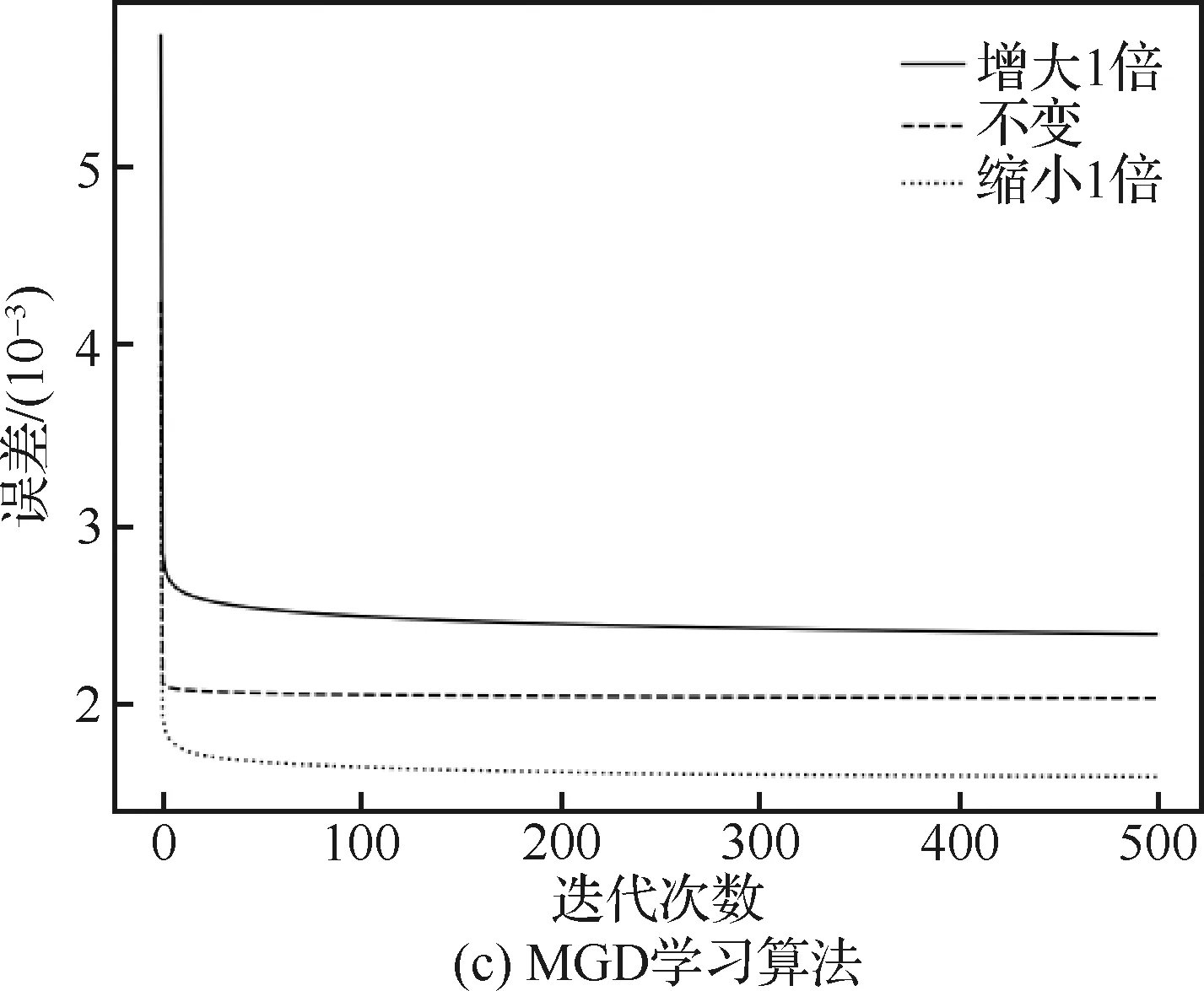
图13 不同权值灰度下各算法误差曲线图Fig.13 Error curve of learning algorithms with different weight greyness
最终,给出动量梯度下降算法学习得到的FGCM模型权值矩阵如下:
⊗=

上述案例仿真结果表明,所提出的MGD算法可以快速减小误差,并稳定在一定范围内,相比于其他学习算法能够兼顾学习精度和收敛速度,且对于权值灰度变化的敏感性最好。
4.4 感性攻击决策模型仿真与分析
在获得典型态势下决策结果后,将其存储在杏仁核决策模板库中。可以将4.2节理性攻击决策FGCM模型的仿真结果作为典型的态势模板存储如下:
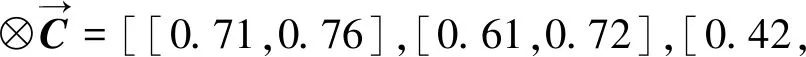
053],[08,08],[08,08],[04,
04],[06,06],[10,10]:[078,084]]
假设,场景1态势下的输入节点的状态为
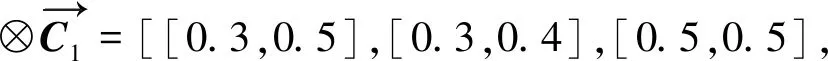
[02,02],[075,075],[04,04],
[04,04],[06,06],[0,0]]
计算与模板态势的相似度为:0.244 38。取=005,此时不满足实施杏仁核决策的触发条件,转入理性攻击决策推理模式。
假设,场景2态势下的输入节点的状态为

[08,08],[075,075],[04,04],
[06,06],[09,09],[0,0]]
计算与模板态势的相似度为:0.034 4,小于误差门限。此时触发杏仁核决策模型,直接得出决策节点的状态值[0.78,0.84]和决策结果“执行攻击”。决策计算过程简单快速,计算耗时为6.2 ms。
5 结 论
本文基于FCM及其扩展模型,开展了复杂不确定战场环境下的多无人机协同攻击决策的建模研究,为提升多无人机执行任务的决策优势提供了理论指导和应用方法参考,主要工作包括:
1) 基于人的决策心智模式,从SoS的角度对多无人机进行任务功能的集成,采用ABFCM建立了包含感性和理性2种决策模式的多无人机协同攻击决策系统模型框架。
2) 基于ABFCM和FGCM建立了包含目标识别与状态估计Agent、意图预测与威胁估计Agent、攻击任务安全性估计Agent和攻击效果估计Agent的多无人机战场态势感知模型,模块化地支撑了协同攻击决策模型的建立。
3) 基于人脑杏仁核机理建立了态势-决策模板快速匹配的感性攻击决策模型,实现了简单、熟悉战场态势条件下的快速决策。
4) 基于直觉模糊集的决策阈值算法建立了理性攻击决策模型,采用MGD学习算法进一步提高了决策模型的学习进化能力,降低了建模工作对专家知识的依赖。
