一种同步时钟偏差和传感器位置误差存在下的TDOA定位新方法
2022-09-05王鼎尹洁昕高路杨宾
王鼎,尹洁昕,*,高路,杨宾
1. 中国人民解放军战略支援部队信息工程大学 信息系统工程学院,郑州 450001 2. 国家数字交换系统工程技术研究中心,郑州 450002 3. 北京航天长征飞行器研究所,北京 100076
众所周知,辐射源定位在无线通信、目标监测、电子对抗、导航遥测等工程领域中具有广阔的应用前景。辐射源定位观测量涵盖空、时、频、能量等多域参数,其中到达时间差(Time Difference of Arrival,TDOA)是应用较频繁的一类观测量。随着现代通信技术和TDOA测量技术的不断发展,基于多个传感器的TDOA定位技术已经成为最为主流的辐射源定位手段之一,该类定位体制适用于宽带信号,能够获得较高的定位精度。
近些年来,国内外学者提出了一系列TDOA定位方法,从计算方式上可分为参数搜索类方法、迭代类方法以及闭式类方法3大类。参数搜索类方法包括网格逐点搜索方法和重要性采样方法等。迭代类方法包括凸优化方法、泰勒(Taylor)级数迭代方法、约束总体最小二乘(Constrained Total Least Squares,CTLS)估计方法以及约束加权最小二乘(Constrained Weighted Least Squares,CWLS)估计方法等。虽然参数搜索类方法和迭代类方法的定位精度都能逼近克拉美罗下界(Cramér-Rao Lower Bound,CRLB),但前者计算量比较庞大,后者大都对迭代初值较敏感,易导致局部收敛。相比较而言,闭式类方法具有更高的计算效率,其中包括球面内插(Spherical-Interpolation,SI)方法、总体最小二乘(Total Least Squares,TLS)估计方法、两步加权最小二乘(Two Step Weighted Least Squares,TSWLS)估计方法以及加权多维标度(Weighted Multidimensional Scaling,WMDS)方法等。SI方法和TLS方法的定位性能难以达到CRLB。TSWLS方法的定位精度虽然能够逼近CRLB,但是该方法产生“门限效应”的误差阈值相对较小,在大观测误差条件下的定位误差会大幅增加。WMDS方法利用了标量积矩阵的维度和特征结构信息,对大观测误差具有更强的鲁棒性,能够获得渐近统计最优的定位精度,是本文研究的重点。
上述TDOA定位方法均假定传感器位置精确已知,当传感器安放在舰载或机载平台,又或是传感器随机布设时,其位置精确值通常无法获知,其中会包含先验观测误差,该误差会严重影响TDOA定位精度。为了抑制此类误差的影响,国内外学者提出了3种方法。第1种方法将传感器位置先验观测误差和TDOA观测误差同等看待,通过重新设置各类估计器中的加权矩阵来提高定位鲁棒性。第2种方法将辐射源位置与传感器位置进行联合估计。第3种方法利用位置精确已知的标校源信息实现目标定位。研究结果表明,第3种方法的定位精度最高,但需要标校源TDOA信息,这在实际中难以获得,而第2种方法不仅可以获得更准确的传感器位置估计值,还比第1种方法具有更高的误差阈值。因此本文主要针对第2种方法展开研究。
除了TDOA观测误差和传感器位置误差外,影响TDOA定位精度的另一个因素是不同传感器之间的同步时钟偏差。在无线传感网络(Wireless Sensor Network,WSN)节点定位领域,国内外学者提出一系列联合定位与时钟同步的有效方法。在一个WSN中,锚节点(位置精确已知或者近似已知)与源节点(位置未知)之间进行单向或者双向通信,基于此可以建立这2类传感节点位置参数与时钟同步参数之间的代数关系,从而实现定位与时钟同步的联合处理。
在上述研究中,一些方法假设传感器时钟偏差完全一致(即完全同步),另一些方法假设各个传感器时钟偏差互不相同(即完全不同步)。然而,这2种建模方式可能与实际情况都不相符。事实上,对于空域中广泛分布的传感器,若2个传感器间距较远,在采集信号时参考的局部时钟易出现差异,但是若2个传感器间距较近,时钟同步则容易得到满足。对此,文献[27]提出一种新的定位观测模型,其依据传感器之间的距离大小将传感器分成若干组,每组传感器共用相同时钟偏差,但不同组之间的时钟偏差互不相同。基于该定位观测模型,文献[27]还提出一种基于TSWLS原理的TDOA定位方法,该方法基于最小二乘估计框架依次给出辐射源位置、传感器位置以及时钟偏差的估计值。为了提高该方法在大观测误差条件下的定位精度,文献[28]提出基于Taylor级数迭代的辐射源位置、传感器位置以及时钟偏差联合估计方法,该方法发生“门限效应”的误差阈值更高,但需要更多计算量,并且易受迭代初始值的影响,可能出现迭代发散和局部收敛等问题。
为了进一步提高定位性能,本文在同步时钟偏差和传感器位置误差同时存在下提出一种基于WMDS原理的TDOA定位方法。该方法的TDOA观测模型借鉴文献[27]中的观测模型,但是定位方法与文献[27]中的方法截然不同,其并不是基于最小二乘估计框架衍生出的,而是根据多维标度分析原理提出的,可以提高对大观测误差的鲁棒性。新方法首先通过构造消元矩阵消除同步时钟偏差的影响;然后基于WMDS原理构建定位关系式,由此获得辐射源位置与传感器位置的估计值;最后利用最大似然估计准则得到同步时钟偏差的估计值。所提方法实现了时钟偏差参数与位置参数的解耦合估计,可以有效抑制时钟偏差和传感器位置误差的影响。最后,本文对新方法的定位精度给出理论性能分析,结果表明其对全部参数的估计精度均能逼近CRLB。仿真实验验证新方法的优越性和理论性能分析的有效性。

表1 本文使用的矩阵等式和不等式Table 1 Matrix equality and inequality used in this paper
1 定位观测模型与问题形成


关于辐射源RDOA的观测模型可以表示为


(1)


(2)
式中:
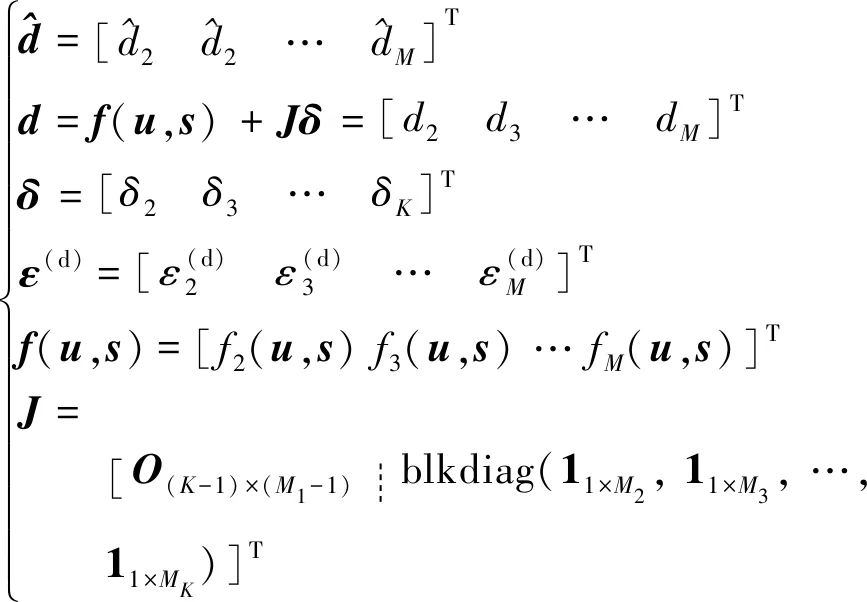
(3)
其中:观测误差服从均值为0、协方差矩阵为的高斯分布;表示同步距离偏差向量。
由于主站位于第1组,所有RDOA观测量均以主站为参考,因此式(1)中第1组等式对应的同步时钟偏差等于0。
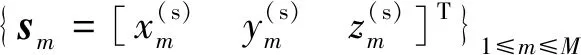
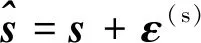
(4)
式中:表示先验观测误差,其服从均值为0、协方差矩阵为的高斯分布,并且与误差向量统计独立。为了便于表述,对先验观测误差进行分块,即
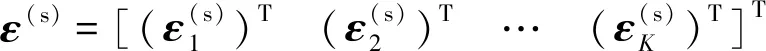
(5)
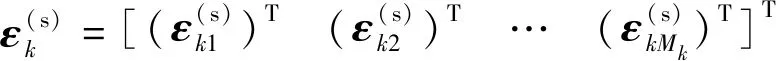
在上述建模过程中,由于RDOA和传感器位置均来自观测,因此应将RDOA观测误差和传感器位置误差建模成随机型误差,而同步时钟偏差并没有先验观测,其是完全未知的参数,因此应按照固定的系统偏差对其进行建模。基于这2类误差模型的差异性,本文将向量和划分成一组参数,将向量单独作为另一组参数,并且实现这2组参数的解耦合估计。
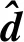
2 新方法的计算原理与步骤
2.1 新方法的原理概述
针对观测模型式(2)的代数特点,新方法的求解原理可概述为以下4点:
1) 线性消元。由于式(2)是部分线性模型,因此可以通过矩阵变换构造矩阵的正交补子空间,从而消除同步距离偏差向量的影响,并形成新的降维观测模型。
2) 多维标度分析。消元后的观测模型仍然具备距离差结构形式,因此可引入多维标度分析方法,构造标量积矩阵,形成定位关系式,并获得位置估计值。
3) 信息补偿。由于在多维标度分析中引入了辅助变量,其与位置向量和相关,因此构建约束优化模型对这部分信息进行有效补偿,以获得渐近统计最优的定位结果。
4) 最大似然估计。在获得位置向量和的估计结果之后,回到最初的最大似然估计模型中对线性参数进行估计,以实现多类型参数的解耦合估计。
基于上述原理概述,本文将新方法的计算过程划分成3个阶段(分别称为阶段a、阶段b以及阶段c),图1描述了其总体技术路线。
下面依次阐述每个阶段的计算原理,并最终给出全部计算步骤。

图1 本文新方法的总体技术路线示意图Fig.1 Schematic diagram of overall technical route of new method proposed in this paper
2.2 阶段a的计算原理
阶段a首先构建消元矩阵以消除同步时钟偏差的影响;接着针对每一组传感器构造标量积矩阵,并利用标量积矩阵的性质形成定位关系式;然后通过一阶误差分析方法推导定位关系式中的误差协方差矩阵,用于确定加权矩阵;最后基于定位关系式和加权矩阵同时获得辐射源位置与传感器位置的估计值。
2.2.1 构建消元矩阵
式(2)是关于向量的线性观测模型,可利用消元矩阵消除其影响,根据矩阵的结构可将消元矩阵写为
=blkdiag(,,…,)∈(-)×(-1)
(6)

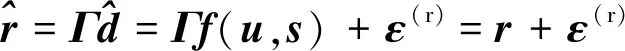
(7)
式中:=(,);=。显然,观测误差服从均值为0、协方差矩阵为=的高斯分布。

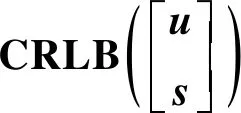
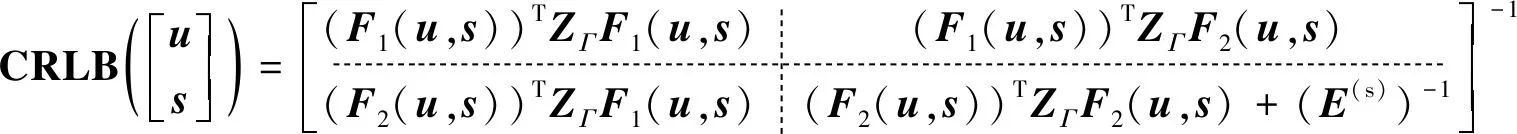
(8)
式中:=()。式(8)的证明见附录B,该式对于本文的理论性能分析至关重要。
为了便于描述,进行向量分块
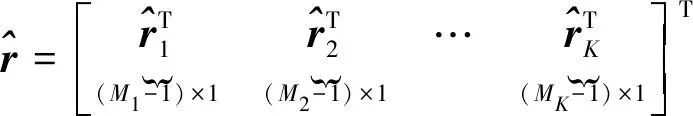
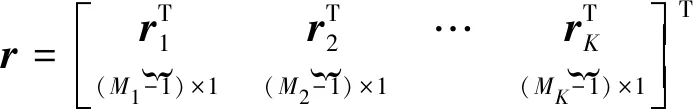

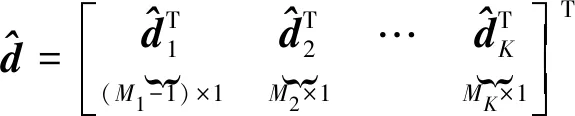
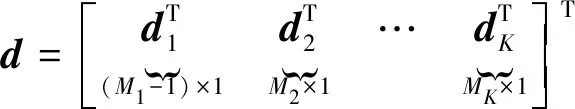
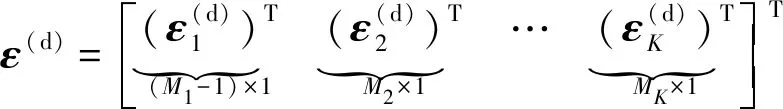
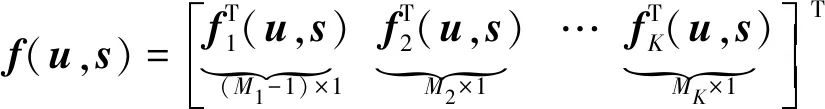
(9)
结合式(7)和式(9)可得

1≤≤
(10)
式中:
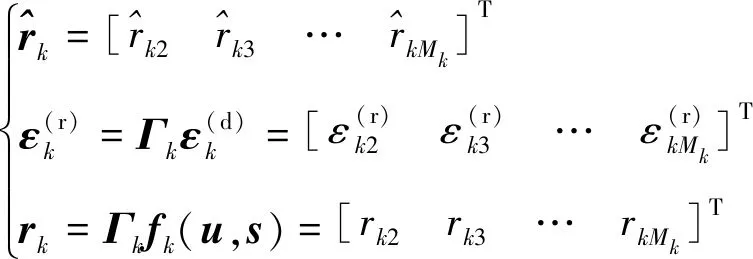
其中:
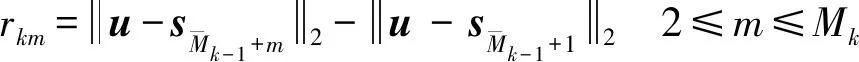
由于向量仍具有距离差的结构形式,因此利用多维标度分析方法对向量和进行联合估计。
2.2.2 构造标量积矩阵及定位关系式
在多维标度分析中需要构造标量积矩阵,文中的定位场景包含组传感器,因此应构造个标量积矩阵。借鉴文献[11,17]中的WMDS定位方法,这里针对第组传感器,首先定义复坐标向量

(11)
式中:j表示虚数单位,其满足j=-1;1=0。利用复坐标向量进一步定义复坐标矩阵

(12)
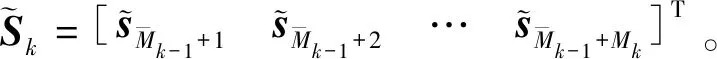
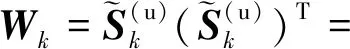
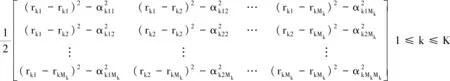
(13)
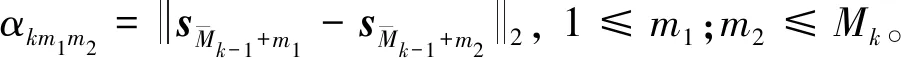
由式(13)可知,针对组传感器构造了个标量积矩阵{}1≤≤,利用它们可以建立定位关系式,首先有结论1。
分别定义实向量和实矩阵
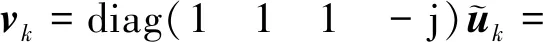
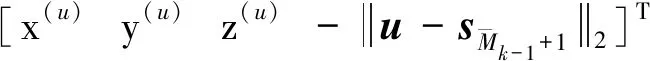
(14)

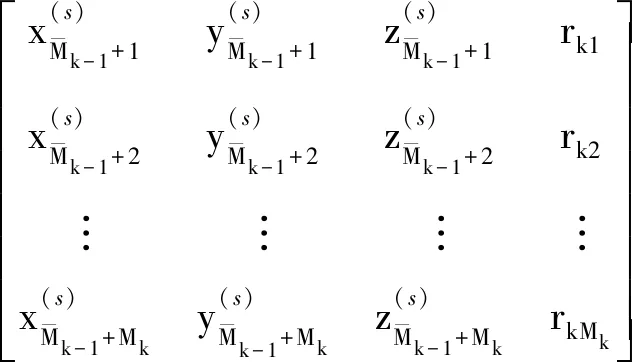
(15)
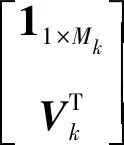
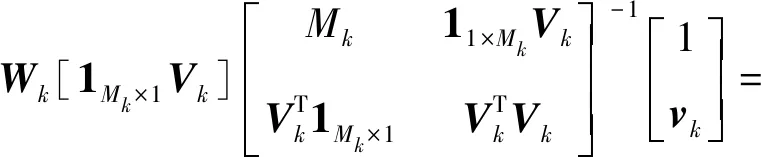
×11≤≤
(16)
结论1的证明见附录C。基于结论1不妨定义矩阵
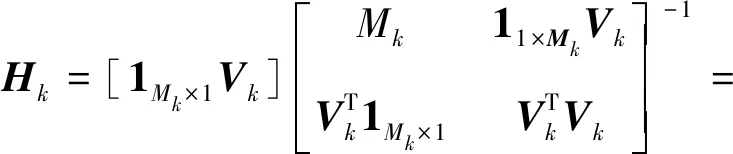

(17)
将式(17)代入式(16)中,并且由向量的定义可知
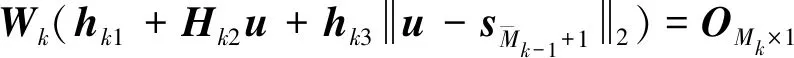
1≤≤
(18)
将式(18)中的个等式进行合并可得
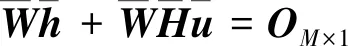
(19)
式中:
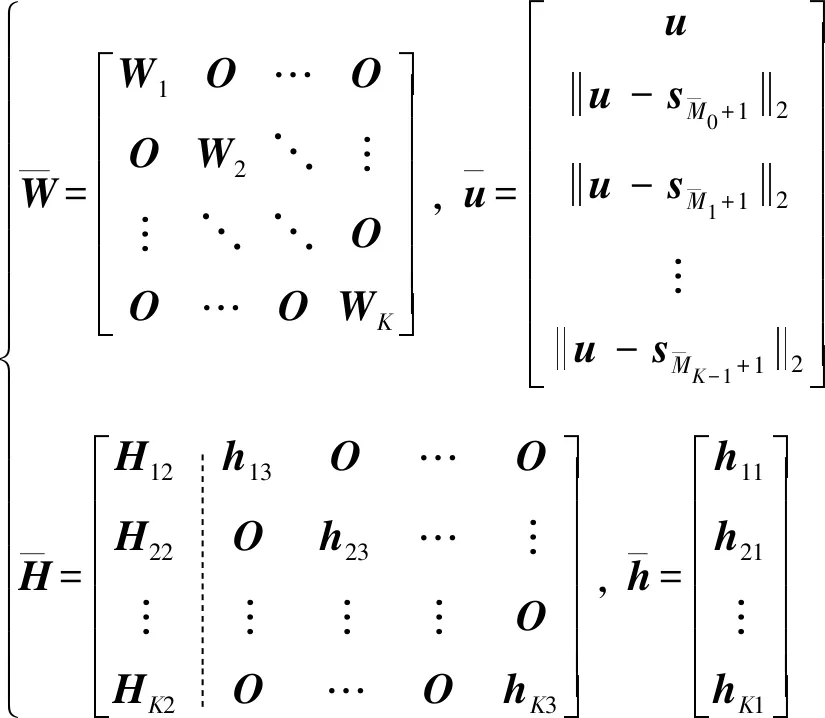
(20)
式(19)为最终获得的定位关系式,利用式(19)可以构建辐射源定位准则。
注意到式(7)中包含-个观测方程,但是式(19)中却包含个观测方程,这意味着式(19)是有冗余的,这种冗余性易导致误差协方差矩阵出现秩亏损现象,文献[11]提出利用正则化技术使其恢复为满秩矩阵,但这仅仅是一种近似处理方式,本文提出利用矩阵正交变换使误差协方差矩阵恢复为满秩矩阵,并且通过理论性能分析证明这种处理方式能够获得渐近统计最优的参数估计精度。
2.2.3 一阶误差扰动分析
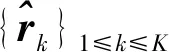

(21)
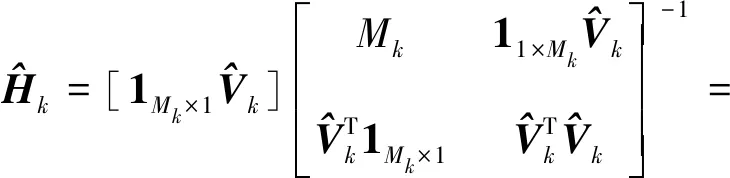
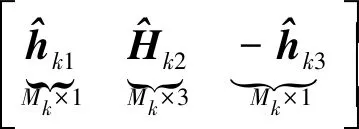
(22)
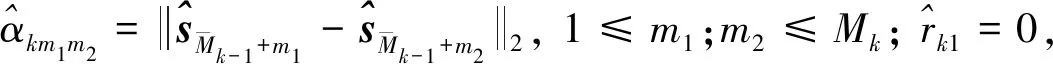
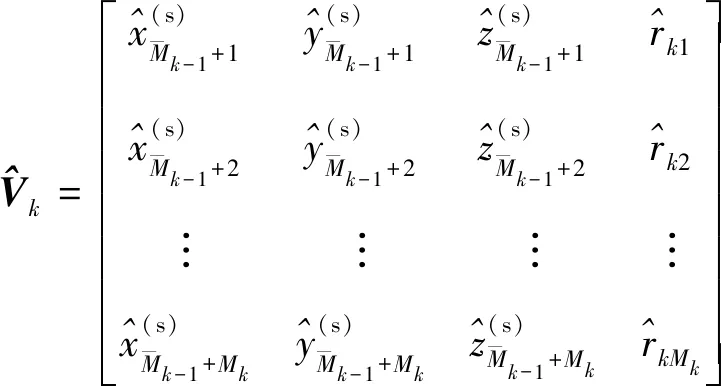
(23)
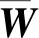
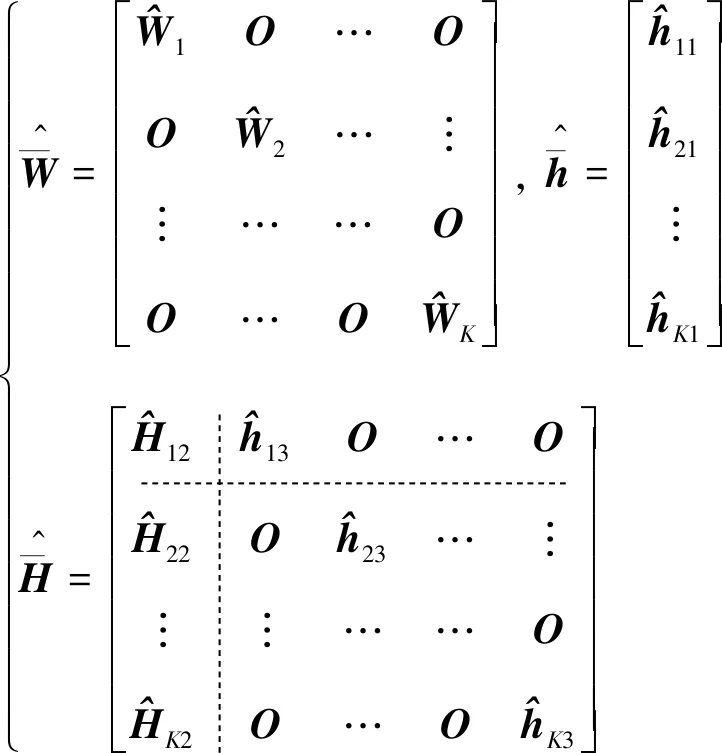
(24)
基于式(19)可以定义误差向量为
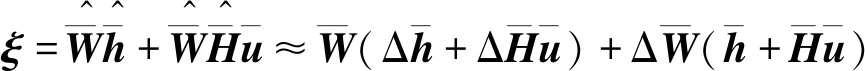
(25)
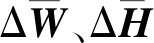

(26)
式中:

(27)
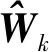
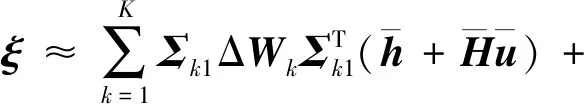
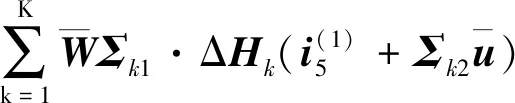
(28)
利用误差矩阵Δ的表达式可以将式(28)右边第1项写成关于观测误差和的线性函数,即
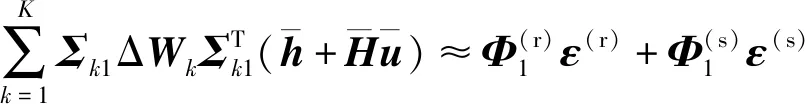
(29)
式中:
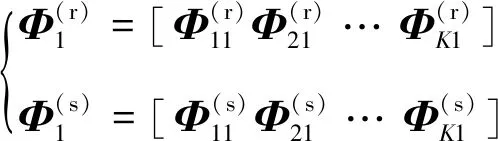
其中:
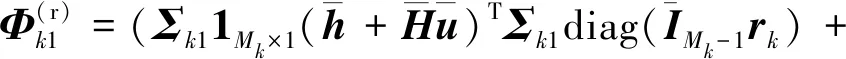
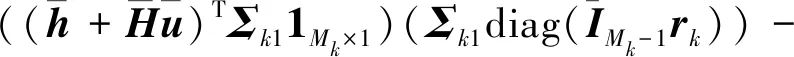
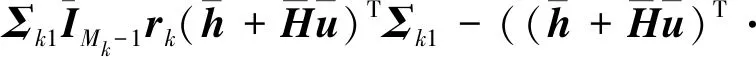
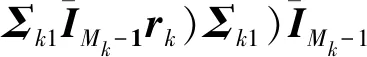
(30)
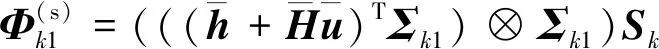
(31)
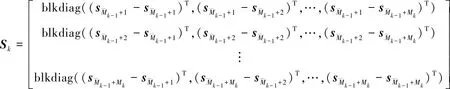
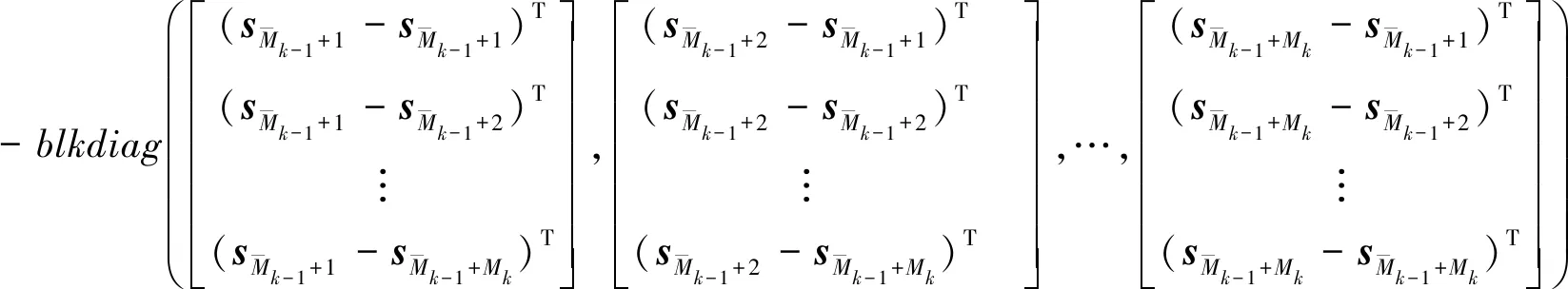
(32)
式(29)的证明见附录E。基于误差矩阵Δ的表达式可以将式(28)右边第2项写成关于观测误差和的线性函数,即

(33)
式中:
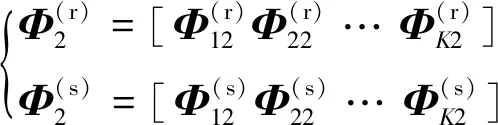
其中:
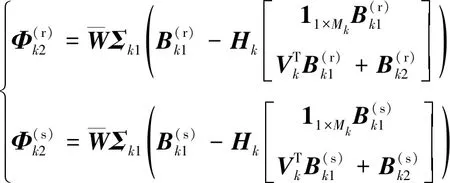
(34)
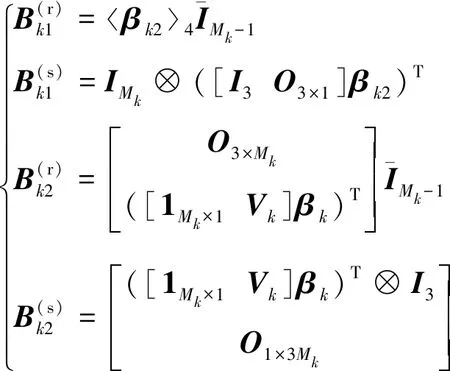
(35)

(36)
式(33)的证明见附录F。
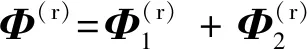
()=()≈()+
()
(37)
在注释5中指出,由于定位关系式存在冗余性,易导致协方差矩阵()出现秩亏损现象,因而无法对该矩阵直接进行求逆运算,下面提出利用矩阵正交变换技术解决该问题。
首先对矩阵进行分解可得

(38)
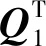


(39)
由式(39)可知,误差向量的协方差矩阵为


(40)

2.2.4 估计准则及其最优估计值
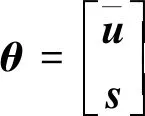

(41)
式中:
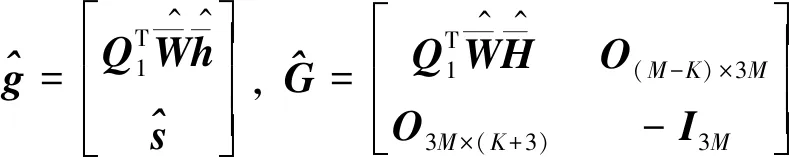
(42)
基于式(41)可以获得阶段a中的估计准则,即

(43)
式中:
()=

(44)
式(43)中的(())可以看成是加权矩阵,其作用在于抑制观测误差和的影响,式(43) 的最优估计值为

(45)

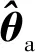
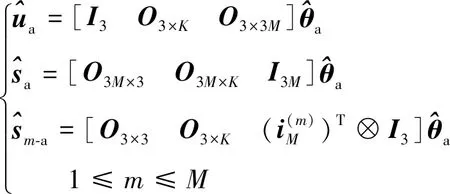
(46)
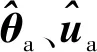
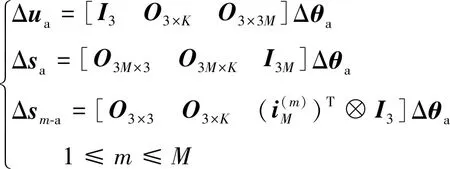
(47)
2.2.5 理论性能分析
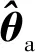
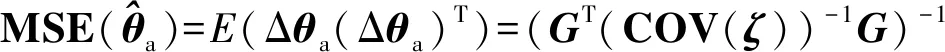
(48)
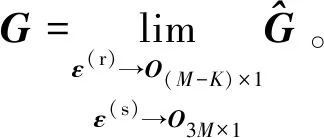

(49)
将式(42)中的第2式和式(49)代入式(48)中可得
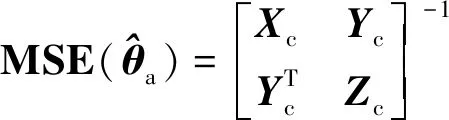
(50)
式中
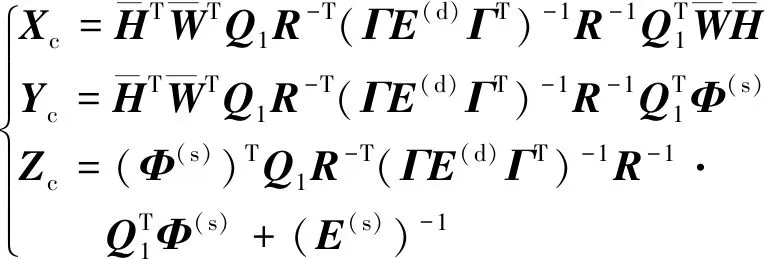
(51)

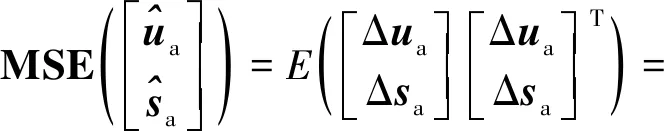
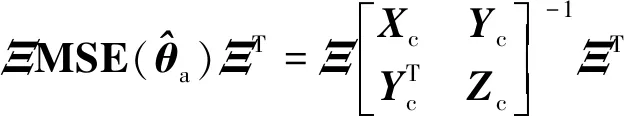
(52)

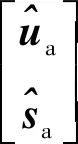
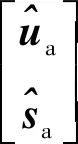
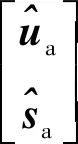
2.3 阶段b的计算原理
向量中的元素间存在约束关系,该约束关系会使得误差向量Δ服从等式约束。阶段b首先基于多维标度分析中引入的辅助变量,构建关于误差向量Δ的约束优化模型,然后基于此模型对误差向量Δ进行估计,最后利用其估计值对阶段a中的定位结果进行更新,以获得渐近统计最优的估计结果。
首先推导误差向量Δ所服从的等式约束。由向量中的第3+个元素的定义可知
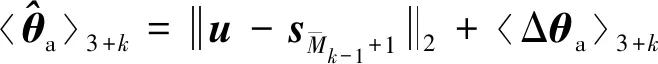
1≤≤
(53)
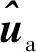
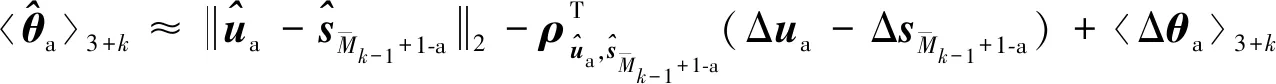
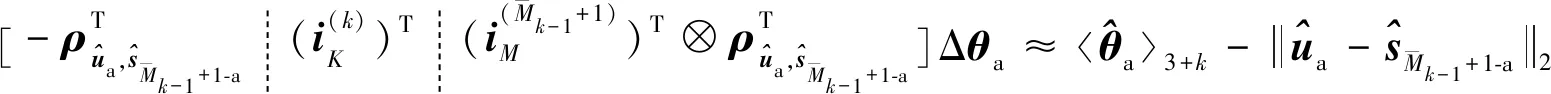
1≤≤
(54)
将式(54)中的个等式进行合并,可以得到关于误差向量Δ的线性等式,即
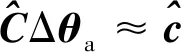
(55)
式中:

(56)
式(55)为误差向量Δ所应满足的等式约束,其是线性等式约束。根据误差向量Δ所服从的高斯分布特性,可以建立估计误差向量Δ的约束优化模型,即
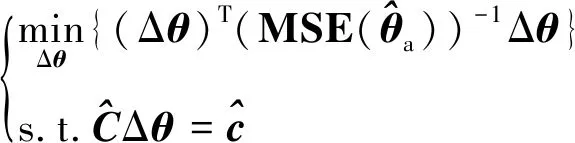
(57)
利用拉格朗日乘子技术可知,式(57)的最优估计值为
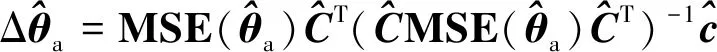
(58)
联合式(47)和式(58)可以得到误差向量Δ和Δ的估计值分别为
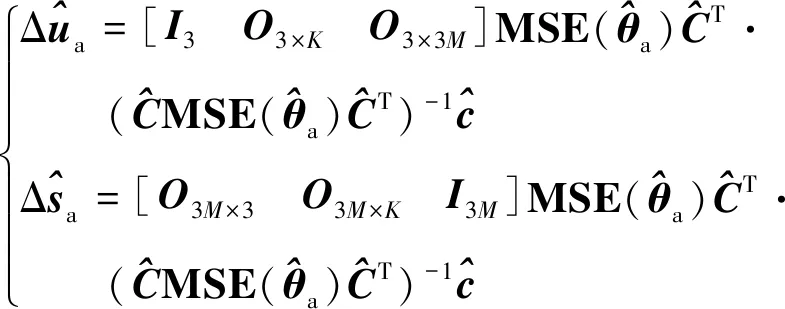
(59)
于是辐射源位置向量和传感器位置向量在阶段b的估计结果为
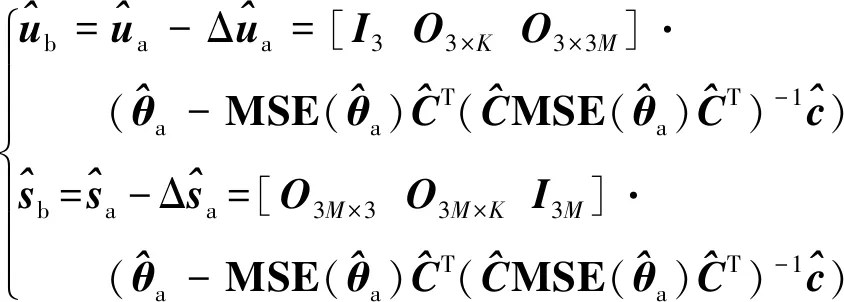
(60)

2.4 阶段c的计算原理与新方法的计算步骤
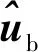


(61)
式(61)是关于向量的二次优化问题,其估计值可以表示为
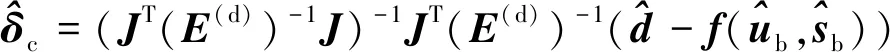
(62)
结合阶段a~阶段c中的描述,下面总结新方法的计算步骤,如图2所示。
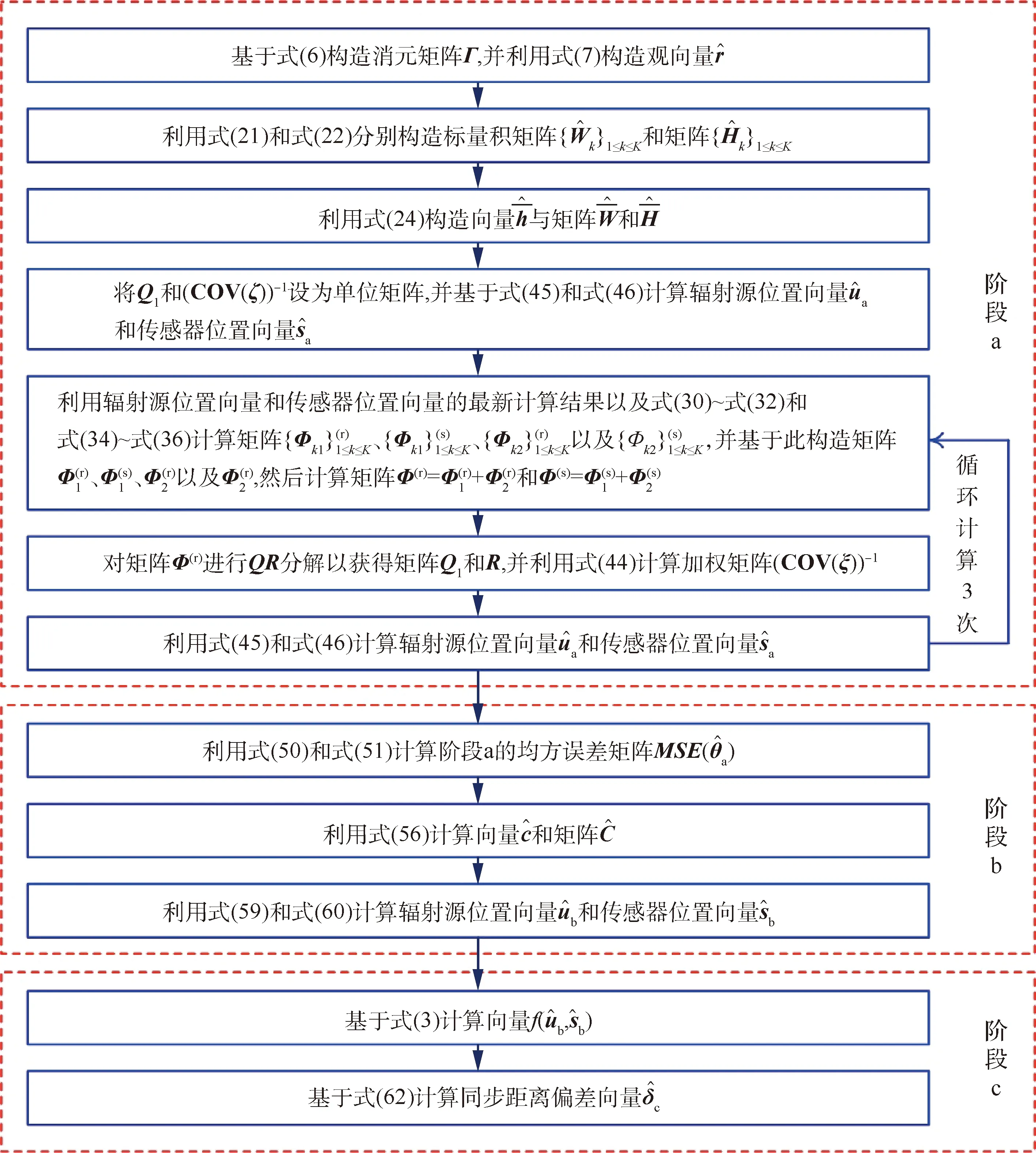
图2 本文新方法的计算流程图Fig.2 Computational flow chart of new method proposed in this paper
下面针对图2中描述的定位方法给出2点注释:
阶段a中的循环计算主要用于更新加权矩阵(()),以提高对大观测误差的稳健性,其每次循环中无需设置迭代步长和收敛准则,并且循环次数是确定的。事实上,现有定位方法很多都需要通过循环计算来更新加权矩阵,以提高定位方法在大观测误差条件下的性能。
新方法的第1步通过消元矩阵消除了同步距离偏差向量的影响,从而实现了该向量与位置向量和的解耦合估计。采用这种求解方式的原因在于:① 只有首先在观测模型中消除向量的影响,才能利用多维标度分析方法对辐射源位置和传感器位置进行估计;② 解耦合估计方法比多参数联合估计方法的计算复杂度更低,在求解过程中可以避免多参数之间的相互影响,具有更高的稳健性。
3 新方法的理论性能分析

3.1 估计值的均方误差及其渐近统计最优性分析
3.1.1 估计均方误差
首先将式(57)中的等式约束代入式(58)中可得
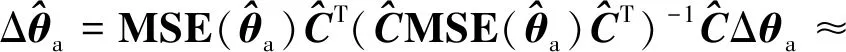
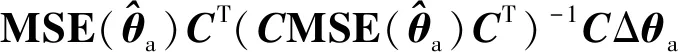
(63)
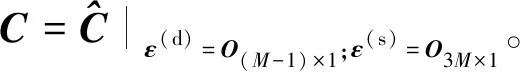
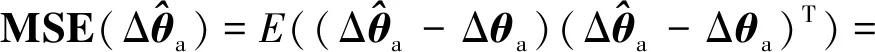
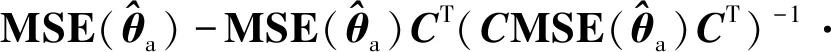
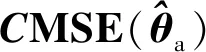
(64)

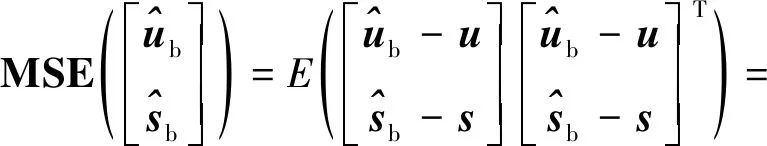

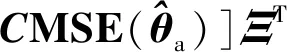
(65)
3.1.2 渐近统计最优性分析


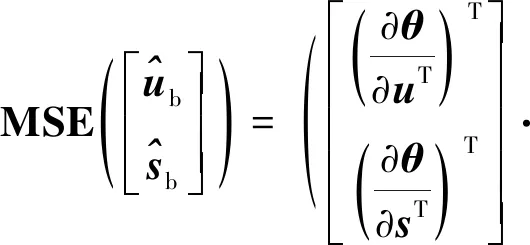
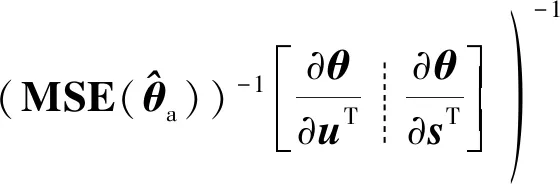
(66)
首先结合式(65)和表1第4个矩阵等式可得


(67)
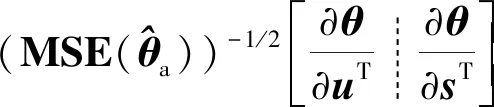

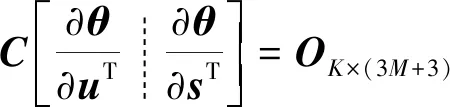
(68)
于是有

(69)
由此可知
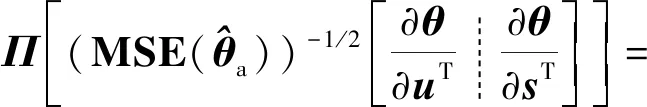
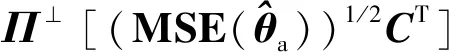
(70)
将式(70)代入式(67)中,并且利用表1第3个矩阵等式可得


(71)
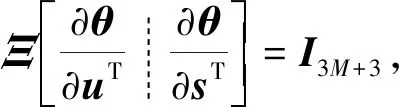
基于结论3还可以进一步得到结论4。
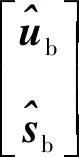
首先结合式(50)和式(66)可得

(72)
将式(51)代入式(72)中的各个子矩阵块中,并且利用式(G3)和式(G4)可知

((,))()(,)
(73)

((,))()(,)
(74)
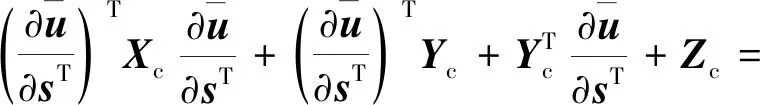
((,))()(,)+()
(75)
将式(73)~式(75)代入式(72)中,并且结合式(8)可知结论4成立。证毕。

3.2 估计值的均方误差及其渐近统计最优性分析
3.2.1 估计均方误差
首先将式(2)代入式(62)中可得
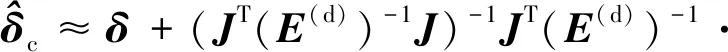
(-(,)Δ-(,)Δ)⟹Δ=
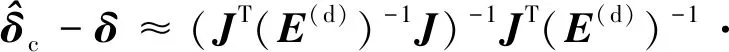
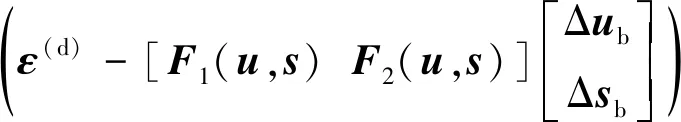
(76)

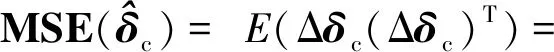
(())+(())()·

()(())--
(77)
式中:
=(())()·

()(())
(78)
3.2.2 渐近统计最优性分析

在一阶误差分析理论框架下,满足=(-1)×(-1)。
首先根据线性参数估计理论和式(48)可得
Δ≈-((()))(())=
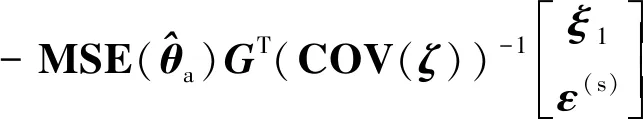
(79)
然后结合式(60)和式(63)可知
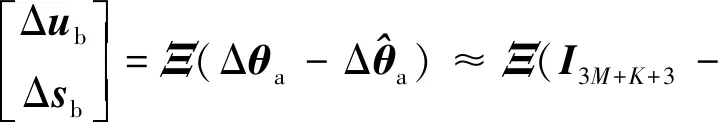
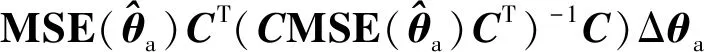
(80)
将式(39)和式(79)代入式(80)中,并且利用关系式=可得

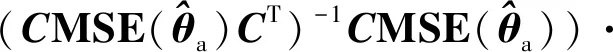
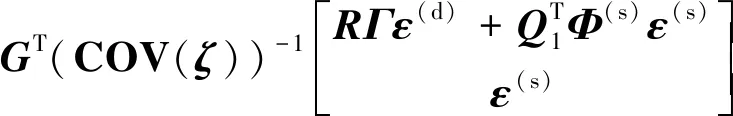
(81)
由式(81)可知
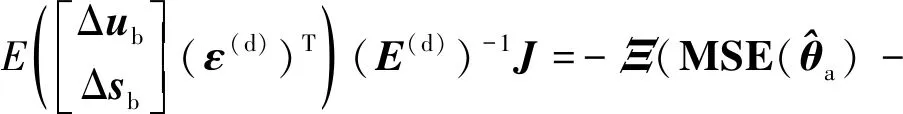

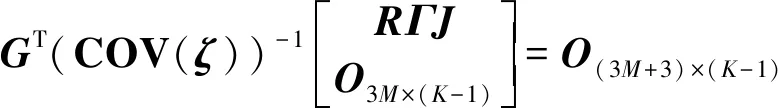
(82)
式中第2个等号利用了关系式=(-)×(-1)。最后将式(82)代入式(78)中可得=(-1)×(-1)。证毕。
将=(-1)×(-1)代入式(77)中,并且结合式(A3)和结论4可知
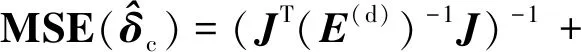
(())()·

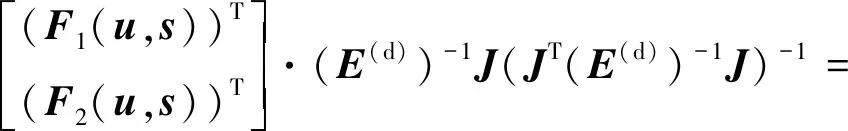
()
(83)
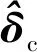
由于最大似然估计器同样具有渐近统计最优性,因此这里有必要讨论文中的新方法与最大似然估计方法之间的关系。首先,阶段c中向量的估计值正是基于最大似然估计准则所获得的。其次,向量和的估计值并不是直接由最大似然估计准则所产生,而是通过对原观测模型进行变换处理后所获得。根据统计信号处理理论可知,对原始观测量进行代数变换后,在不损失观测信息并且合理设置加权矩阵的条件下,能够得到与最大似然等价的估计结果,这正是本文所采取的处理方式。因此,文中的新方法可以看成是最大似然估计方法的一种近似实现方式。另一方面,由于原观测模型式(2)的非线性特征,2种方法的理论性能分析中都不可避免需要进行一阶近似,当“门限效应”尚未产生时,一阶近似误差是可以忽略的,但是当“门限效应”产生时,一阶近似误差的影响就会逐渐显现,但何时产生“门限效应”尚无完备的理论支撑,每种方法的主要区别在于产生“门限效应”时的误差阈值大小。
4 仿真实验

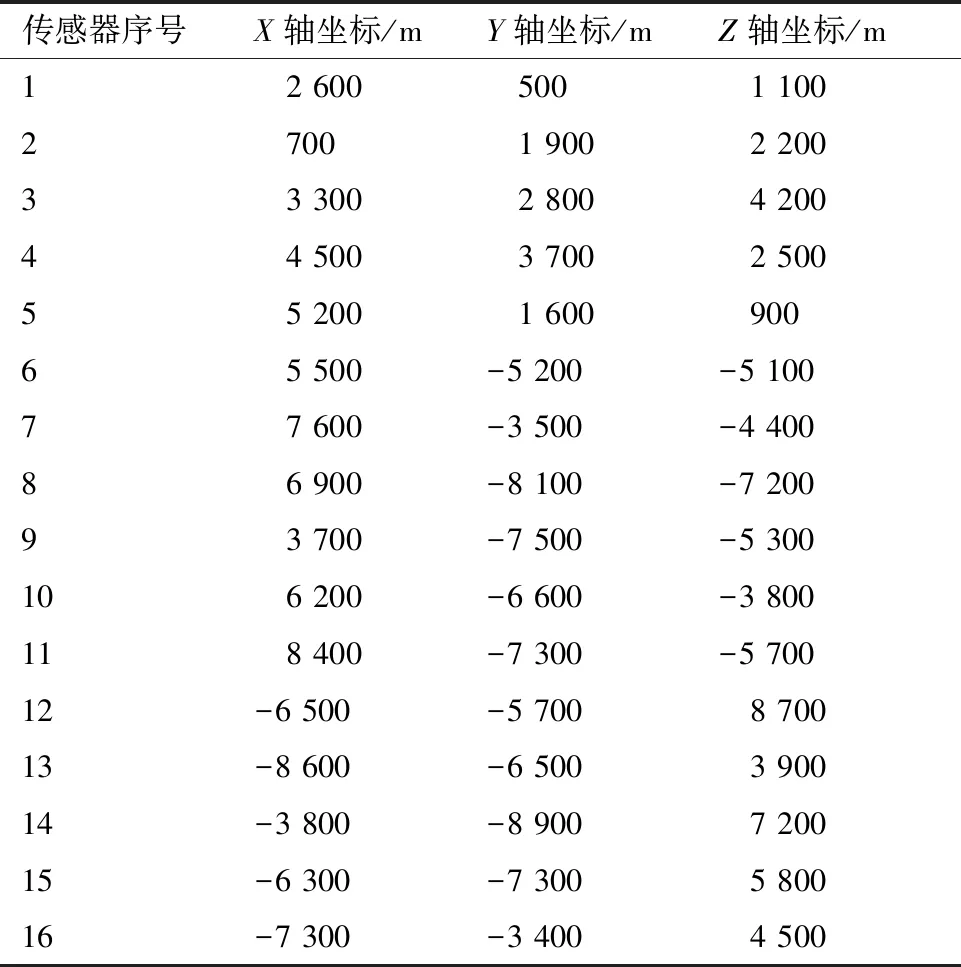
表2 传感器3维位置坐标Table 2 3D position coordinate of sensors
将辐射源位置向量设为=[6 000, 6 000, 6 000]m,将同步距离偏差向量设为=[0, 50, 70]m,并令20lg()=0 dBm和20lg=5 dBm,下面利用文中的新方法对辐射源进行定位,并且进行5 000次蒙特卡罗实验,图3给出了辐射源定位结果散点图与定位误差椭圆曲线,图中的椭圆曲线是利用文献[31]中的方法计算所得。
从图3中可以看出,定位结果散点图形状与定位误差椭圆形状一致,并且大概率对应大面积椭圆,小概率对应小面积椭圆,验证了新方法的有效性。
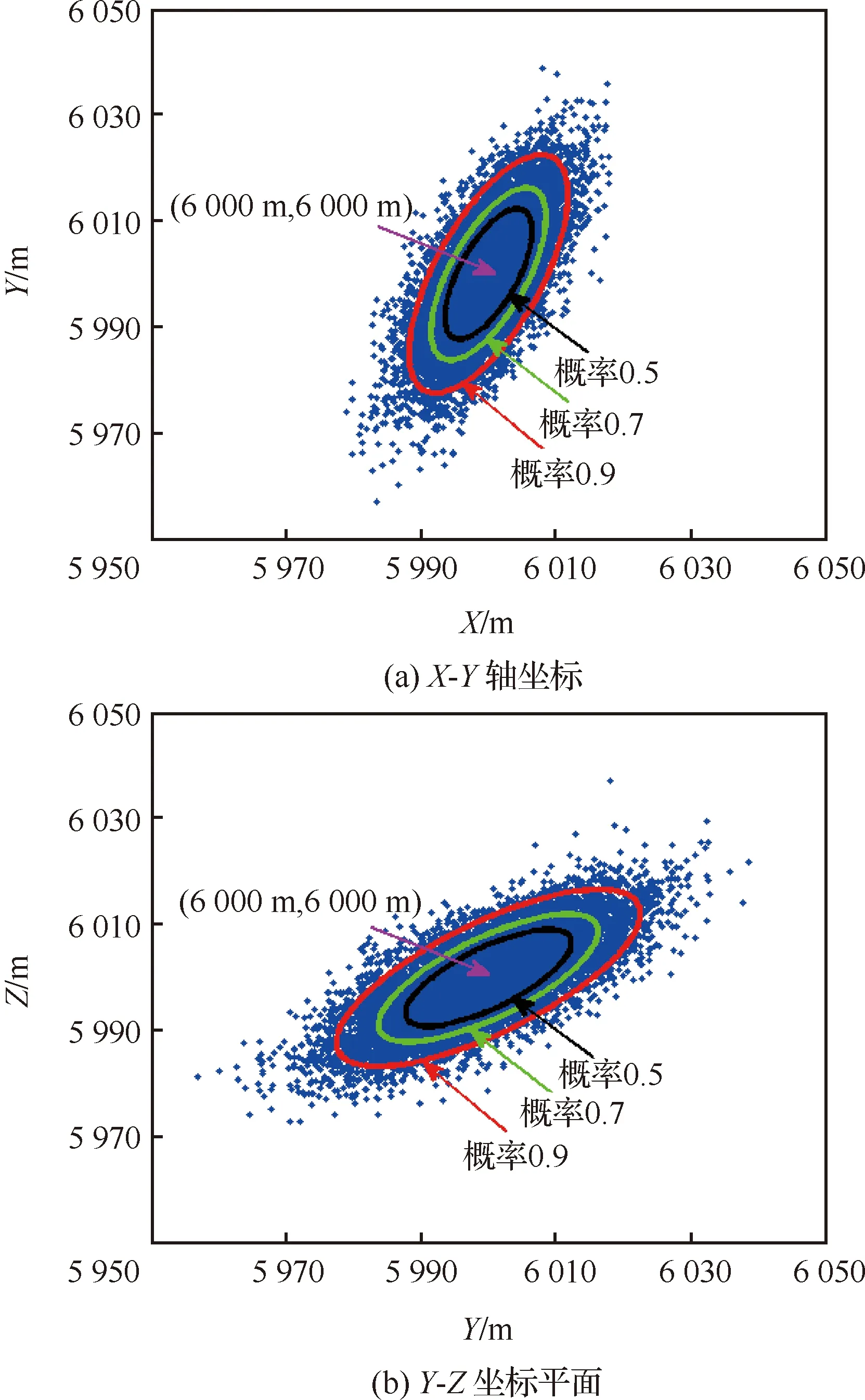
图3 辐射源定位结果散点图与定位误差椭圆曲线Fig.3 Scatter diagram of emitter location result and ellipse curve of location error
这里将本文新方法与文献[17]中的WMDS定位方法、文献[27]中的闭式定位方法以及文献[28]中的迭代定位方法(实质上就是最大似然估计方法)进行比较,用于验证新方法的优越性。需要指出的是,文献[17]中的WMDS定位方法并未考虑同步时钟偏差的影响,而且该方法仅给出了辐射源位置估计结果,所以无法与其比较传感器位置和同步距离偏差的估计精度。此外,与新方法相类似,文献[27]中的闭式定位方法和文献[28]中的迭代定位方法也具有渐近统计最优性,因此需要在大观测误差条件下比较参数估计精度。将辐射源位置向量设为=[8 600, 9 200, 8 500]m,将同步距离偏差向量设为=[0, 150, 180]m,首先令20lg=20 dBm,图4分别给出了辐射源位置、传感器位置以及同步距离偏差估计均方根误差随着参数的变化曲线;然后令20lg=15 dBm,图5分别给出了辐射源位置、传感器位置以及同步距离偏差估计均方根误差随着参数的变化曲线。
从图4和图5中可以看出:① 新方法的定位精度明显优于文献[17]中的WMDS定位方法,这是因为后者并未考虑同步时钟偏差的影响,而同步时钟偏差属于系统偏差,当该偏差出现时会使得文献[17]中的定位观测模型失配,从而使其定位方法变成有偏估计方法,并最终导致估计性能急剧下降,甚至失效;② 在大观测误差情形下,新方法的估计精度高于文献[27]中的闭式定位方法,前者产生“门限效应”的误差阈值更高,这正是多维标度分析方法所带来的性能增益;③ 当文献[28]中的迭代定位方法取随机值作为迭代初始值时,其在大观测误差情形下的估计误差要明显大于新方法,这里的随机值是指在真实值的基础上叠加一定的高斯随机误差;④ 当文献[28]中的迭代定位方法取真实值作为迭代初始值时,其估计精度与新方法接近,但是将真实值作为迭代初始值在实际应用中难以实现,而新方法并不存在此问题,并且计算复杂度更低(见表3);⑤ 新方法的参数估计均方根误差能够逼近相应的CRLB,从而验证第4节理论性能分析的有效性。
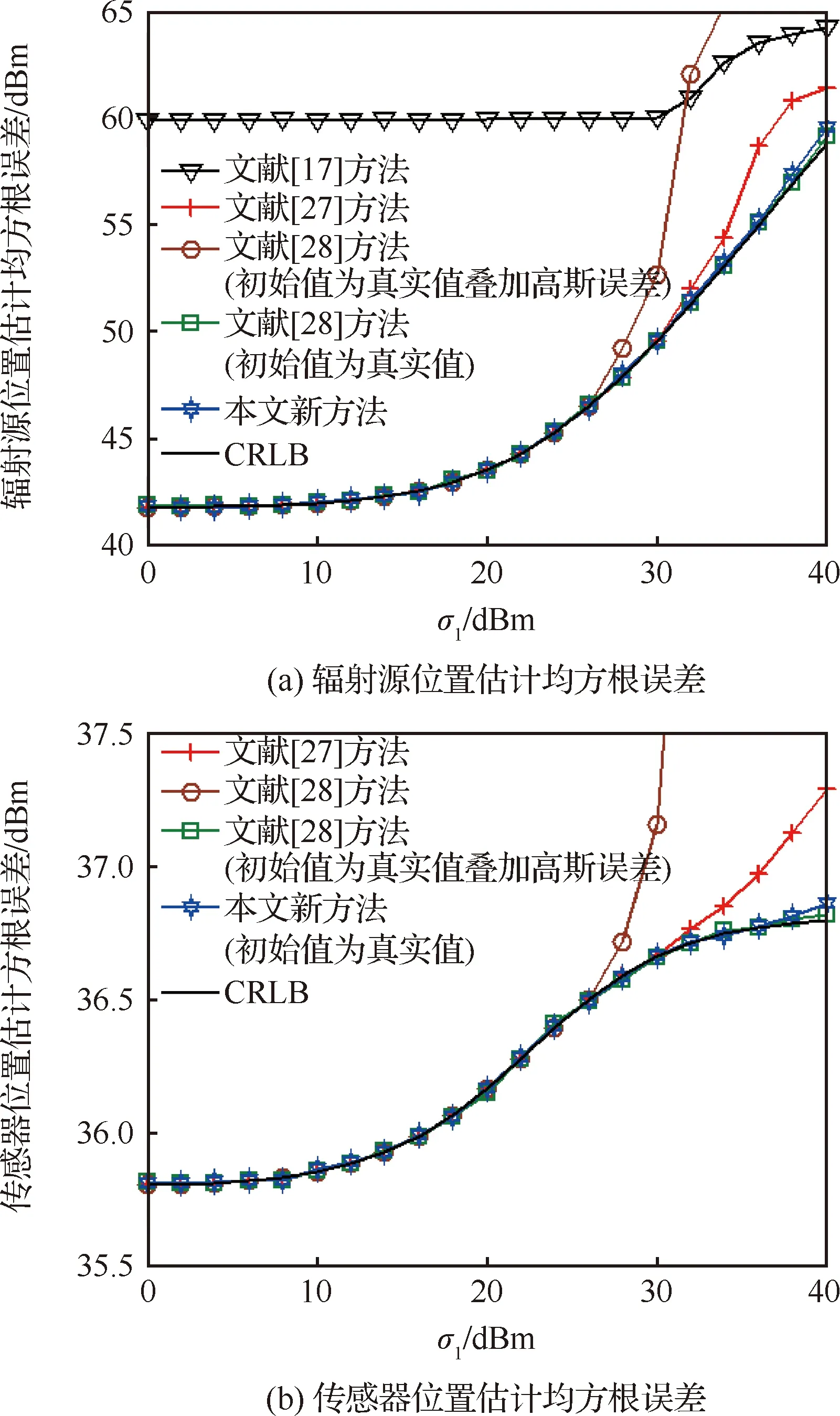
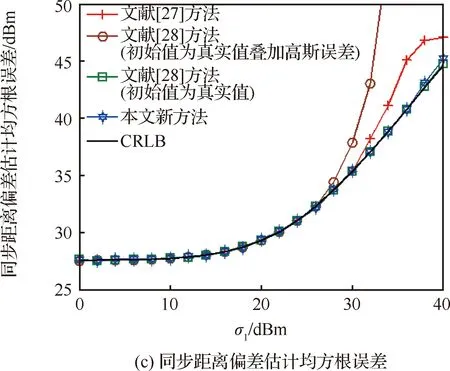
图4 辐射源位置、传感器位置和同步距离偏差的估计均方根误差随参数σ1的变化曲线Fig.4 Curves of RMSE of emitter position, sensor position and synchronization distance bias estimation as a function of σ1
本节的最后将文中的新方法与文献[27]中的闭式定位方法以及文献[28]中的定位迭代方法的运行时间进行比较,用于间接说明3种定位方法的计算复杂度。仿真软件为MATLAB R2020a,仿真程序在安装有i7-3520 CPU的PC机上运行,令20lg=15 dBm和20lg=20 dBm,其余条件不变,并进行5 000次蒙特卡罗实验。表3给出了3种定位方法的平均运行时间。从表3中可以看出,新方法的计算复杂度略高于文献[27]中的闭式定位方法,但是明显低于文献[28]中的迭代定位方法。


图5 辐射源位置、传感器位置和同步距离偏差估计均方根误差随参数σ2的变化曲线Fig.5 Curves of RMSE of emitter position, sensor position and synchronization distance bias estimation as a function of σ2
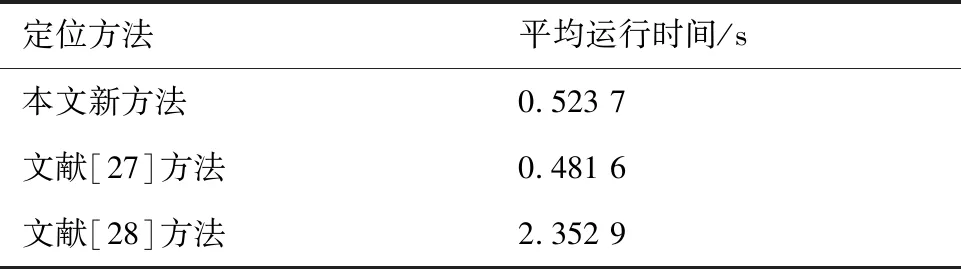
表3 3种定位方法的平均运行时间Table 3 Average running time of three localization methods
5 结 论
本文在同步时钟偏差和传感器位置误差同时存在的条件下研究了TDOA定位问题,主要结论包括:
1) 提出了一种基于加权多维标度分析的TDOA定位新方法,并利用一阶误差性能分析方法推导了新方法的参数估计性能,证明了其估计性能能够渐近逼近CRLB。
2) 仿真实验结果验证了新方法的有效性和渐近统计最优性。
3) 新方法的性能与初始值为真实值的迭代方法接近(以文献[28]中的迭代定位方法为比较对象),相比于文献[27]中的闭式定位方法,其产生“门限效应”的误差阈值更高,对于大观测误差具有更强的鲁棒性。
