一种基于切换拓扑的离散时间一致性协议
2020-06-12杜宇凡
杜宇凡
(广东工业大学计算机学院 广东省广州市 510006)
近年来,多智能体系统协同控制方面的研究取得了突破性的进展。一致性协议是多智能体理论中的一个核心问题。设计一致性协议旨在使得智能体状态在协议控制下最终能达到一致性。
Krause等人[1]提出了一种基于切换拓扑的离散时间一致性协议,即经典的Hegselmann—Krause模型,各智能体取其通信范围内的邻居智能体的状态平均值作为下一次迭代状态。在该协议下,多智能体系统通常不能始终保持连通,系统最终会演化成多个小群体,每个小群体之间的距离超过通信范围,不再相互通信。
Zheng等人[2]提出了一种基于切换拓扑的离散时间一致性协议,各智能体取其自身状态与通信范围内的邻居智能体的组合状态作为下一次迭代状态。Zheng[2]等人证明了,在该协议下,如果多智能体系统能始终保持连通,且调整因子满足小于时,系统最终能收敛到全局的状态平均值。
Xie等人[3]提出了一种基于切换拓扑的离散时间一致性协议,各智能体取其自身状态与通信范围内的最近邻居智能体的组合状态作为下一次迭代状态。该方法只需考虑两侧的最近邻居智能体的状态信息,大大减少了计算量。Xie等人[3]证明了,在该协议下,如果多智能体系统能始终保持连通,且调整因子满足小于时,系统最终能收敛到全局的状态平均值。调整因子的范围进一步扩大,这样有助于加快系统的收敛速度。
然而,怎样才能保证多智能体系统始终保持连通?上述一致性协议都没有涉及到这个关键问题。一旦系统在演化过程中丧失了连通性,智能体的状态值就不能达成一致。本文从保持连通性的角度出发,设计了一种改进的Hegselmann-Krause一致性协议,使得多智能体系统可以始终保持连通,并最终一定能达成一致。
本文的章节安排如下:II章节主要介绍一些阅读本文所必需的基础知识,包括图论与矩阵论,离散一致性协议等等,并在末尾对本文研究的主要问题做了简单的阐述。III章节陈述了本文的主要结果,提出了一种基于切换拓扑的离散时间一致性协议。IV章节通过仿真实验验证了该协议的有效性。最后,V章节给出了本文的结论和未来的研究展望。
1 预备知识及问题描述
1.1 图论与矩阵论
我们把一个具有n个智能体的多智能体系统描述为一个具有n个顶点的无向图其中V是图G的顶点集,满足是顶点的顺序标号。E是图G的边集,满足图G的一条边表示一对顶点i和j互为邻居,邻居之间可以彼此接收到对方发送出的信息。顶点i的邻居集可表示为是图G的邻接矩阵,其元素与边相关:。
引理 图G的拉普拉斯矩阵L具有以下性质:
(1)0是矩阵L的一个特征值,1是其对应的特征向量,满足L1=0;
(2)如果图G是连通无向图,那么0是矩阵L的单一特征值;
(3)如果图G是连通无向图,那么矩阵L是对称正半定矩阵且有n个非负实数特征值,可按升序排列为其中被称为图G的代数连通度。
1.2 离散一致性协议
考虑一个具有n个智能体的多智能体系统,这些智能体的状态值处于一个实数集R。我们用G={V,E,A}表示智能体所对应的图结构,每个智能体的状态值用xi(k)表示,其中k为迭代次数。
Krause等人[1]提出了一种基于切换拓扑的离散时间一致性协议:

即智能体i下一次的状态为所有邻居智能体(包括自身)的状态平均值。系统不能达成一致性,会演化成多个观点值。
Zheng等人[2]提出了一种基于切换拓扑的离散时间一致性协议:
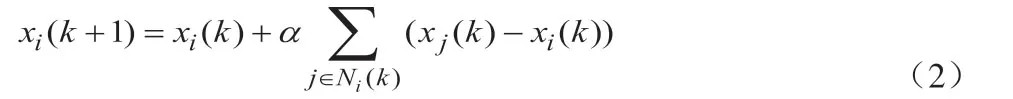
即智能体i下一次的状态为其自身状态与通信范围内的邻居智能体的组合状态。Zheng[2]等人通过李雅普诺夫函数理论证明了在该协议下,若多智能体系统能始终保持连通,且调整因子a满足小于时,系统最终能收敛到全局的状态平均值。
Xie等人[3]提出了一种基于切换拓扑的离散时间一致性协议:
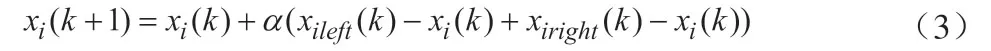
即智能体i下一次的状态为其自身状态与通信范围内的最近邻居智能体的组合状态,是智能体i两侧的最近邻居智能体的状态。Xie等人[3]通过李雅普诺夫函数理论证明了在该协议下,若多智能体系统能始终保持连通,且调整因子a满足小于时,系统最终能收敛到全局的状态平均值。以上两个一致性协议(2),(3)都是假设系统能保持连通,但是系统往往不能始终保持连通。一旦系统连通性不能保持,一致性就不能达成。我们在下文中提出了一种离散一致性协议,保证系统能始终保持连通,并能稳定地达成一致性。
1.3 问题描述
对于任意的智能体初始状态向量x(0),和智能体i,j=1,...,n,如果存在离散一致性协议使得各智能体状态在有限次迭代次数内最终趋于一致,则称该协议解决了一致性问题。
2 主要结果
我们给出如下定义:
智能体i下一次的状态为自身状态和两侧最远邻居智能体状态的平均值。若智能体i的左邻域为空集,即左侧没有最远邻居,则忽略左邻域,只考虑右侧的最远邻居;若智能体i的右邻域为空集,即右侧没有最远邻居,则忽略右邻域,只考虑左侧的最远邻居。
以上描述用一致性协议描述如下:
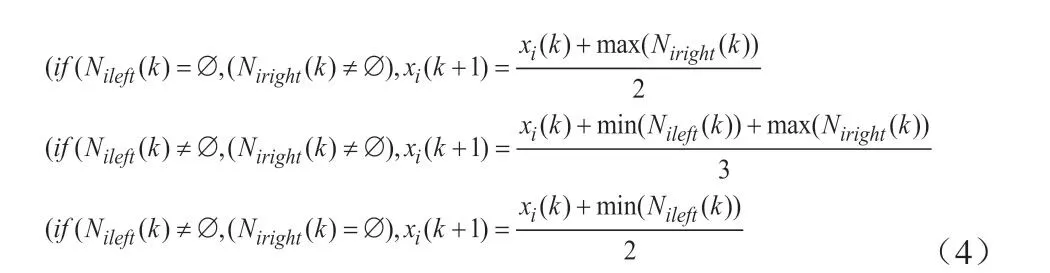
接下来,我们将证明,对于初始时刻连通的初始拓扑,在一致性协议(4)下系统一定能保持连通性,并最终一定能达成一致性。
定理1:如果两个智能体i,j在第k次迭代中具有相同的状态,那么这两个智能体i,j在第k+1次迭代中具有相同的状态。即如果
证明:如果两个智能体i,j在第k次迭代中具有相同的状态,它们就有着相同的两侧最远邻居,那么在k+1次迭代中,两个智能体i,j也会具有相同的状态。
特别地,如果两个智能体i,j在第k次迭代中具有相同的状态,那么它们在随后的迭代中就有相同的状态。
定理2:对于初始时刻连通的初始拓扑,在第k次迭代中,边界智能体(状态值最大的和最小的智能体)有且仅有一个邻居,其余智能体有且仅有两个邻居。状态值最小的智能体,其左邻域为空集,在右邻域上有且仅有一个邻居;状态值最大的智能体,其右邻域为空集,在左邻域上有且仅有一个邻居。
证明:基于初始时刻连通的初始拓扑,对于除了边界智能体以外的智能体,它们在左右邻域上一定能搜索到智能体作为它的邻居,所以它们一定会有两个邻居。而状态值最小的智能体在左邻域上搜索不到邻居,只有在右邻域上能搜索到邻居;状态值最大的智能体在右邻域上搜索不到邻居,只有在左邻域上搜索到邻居。
定理3:对于初始时刻连通的初始拓扑,假设有两个非边界智能体i,j,满足那么智能体i,j在其左右邻域的最远邻居满足:
定理4:对于初始时刻连通的初始拓扑,在一致性协议(4)下系统一定能保持连通性。即如果系统在第k次迭代中是连通的,系统在第k+1次迭代中就一定是连通的。
证明:假设在第k次迭代中系统n个智能体的状态值为
由于系统在第k次迭代中是连通的,因此依次有序的两智能体的状态值的差值均小于r,即
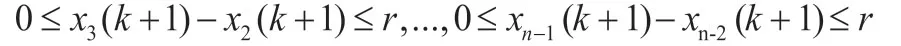
则根据定理2,智能体i和j均有两个邻居,那么有
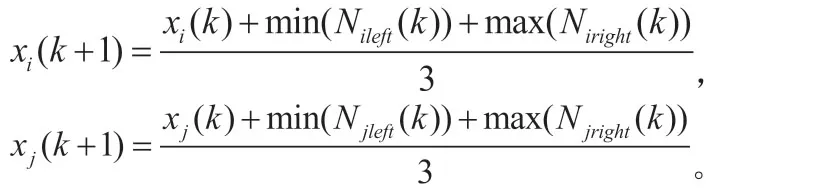
然后我们讨论边界智能体xn(k)在k+1次迭代中可能会发生的情况。

于是我们可知,如果系统在第k次迭代中是连通的,系统在第k+1次迭代中就一定是连通的。证毕。
定理5:对于初始时刻连通的初始拓扑,在一致性协议(4)下系统一定能达成一致性。
证明:我们首先证明,在每一次的系统迭代中,系统的最大状态值单调递减,系统的最小状态值单调递增。
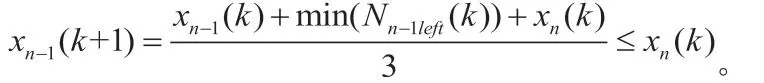

于是我们又在每一次的系统迭代中,系统的最大状态值单调递减,类似地,系统的最小状态值单调递增。系统的区间长度在不断减小。
而根据定理4,系统在迭代过程中又能一直保持连通,那么在有限次的迭代次数中,必定存在一个迭代次数t,使得系统的区间长度小于r。
当到达这个迭代次数t时,状态值最大的智能体在左邻域上选择的邻居就是状态值最小的智能体,状态值最小的智能体在右邻域上选择的邻居就是状态值最大的智能体。于是,在t+1次迭代中,这两个智能体的状态发生了重合,它们的状态值等于在t次迭代中这两个智能体的状态平均值。
在后续的迭代次数中,系统的区间长度仍在不断减小。但是系统中智能体的状态值至少会两两重合一次。那么经过有限次的迭代次数后,系统中的所有智能体的状态值会完全相同,即系统一定能达成一致性。
于是我们可知,对于初始时刻连通的初始拓扑,在一致性协议(4)下系统一定能达成一致性。证毕。
3 仿真实验
本文的仿真实验是基于Matlab数学软件来进行的。在仿真实验中,以智能体的位置信息作为状态值,以智能体进行汇聚为例,考虑初始时刻系统的初始拓扑是连通的。我们以Xie等人在[3]中提出的基于切换拓扑的离散时间一致性协议作为对比对象,主要讨论本文提出的一致性协议和该协议在性能上的共同点和不同点。
对于两种一致性协议而言,每一个智能体在进行状态演化的过程中,都只需要存储和计算自身和两个邻居智能体的状态信息([3]中的协议(3)是选择两个与自身状态差值最近的智能体,而本文是选择两个与自身状态差值最远的智能体),因此在每一步的迭代过程的计算量都只需要两次,两种协议在系统演化所需要的计算资源上是相同的。
但是,当系统的初始拓扑是随机分布的情形时,[3]中的协议不一定能保证系统拓扑在智能体的状态演化过程中始终保持连通,系统拓扑可能不会收敛到一致性。而本文提出的一致性协议(4),经过了严格的证明分析,无论系统的初始拓扑是何种情形,系统拓扑在智能体的状态演化过程中一定能保持连通,并能收敛到一致性。而且,本文的邻域选取策略是选择两个与自身状态差值最远(而非最近)的邻居智能体,因此一致性协议(4)的收敛速度上比[3]中的协议(3)有较明显的加快。
接下来,我们通过对[3]中的一致性协议(3)和本文提出的一致性协议(4)进行四组仿真实验,作出对比分析。每一组仿真实验中智能体的初始状态信息是相同的,即1)和2),3)和4),5)和6),7)和8)中的多智能体系统具有相同的初始拓扑。
1.一致性协议(3):11个智能体的状态值均匀分布在[0,5]的区间内,通信半径r=1,调整因子。在智能体的状态演化过程中系统拓扑始终保持连通,经过约100次迭代后,11个智能体的状态值达成一致,汇聚在一个点2.5上,具体情况如图1所示。
2.一致性协议(4):11个智能体的状态值均匀分布在[0,5]的区间内,通信半径r=1。在智能体的状态演化过程中系统拓扑始终保持连通,经过约15次迭代后,11个智能体的状态值达成一致,汇聚在一个点2.5上,具体情况如图2所示。
3.一致性协议(3):20个智能体的状态值均匀分布在[0,10]的区间内,通信半径r=1,调整因子。在智能体的状态演化过程中系统拓扑始终保持连通,经过约300次迭代后,20个智能体的状态值达成一致,汇聚在一个点5上,具体情况如图3所示。

图1:协议(3)下初始拓扑均匀分布在区间[0,5]的演化过程
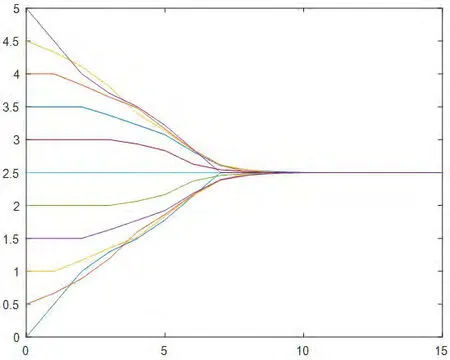
图2:协议(4)下初始拓扑均匀分布在区间[0,5]的演化过程
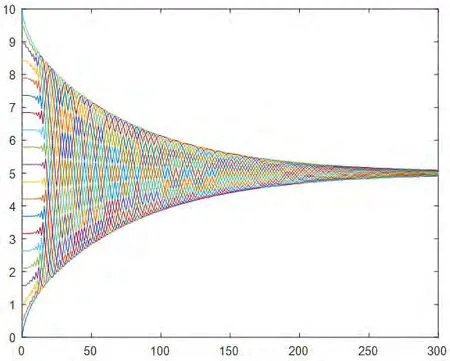
图3:协议(3)下初始拓扑均匀分布在区间[0,10]的演化过程
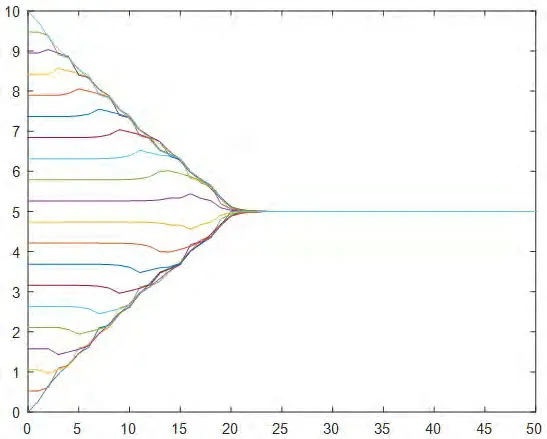
图4:协议(4)下初始拓扑均匀分布在区间[0,10]的演化过程
4.一致性协议(4):20个智能体的状态值均匀分布在[0,10]的区间内,通信半径r=1。在智能体的状态演化过程中系统拓扑始终保持连通,经过约50次迭代后,20个智能体的状态值达成一致,汇聚在一个点5上,具体情况如图4所示。
5.一致性协议(3):11个智能体的状态值随机分布在[0,5]的区间内,通信半径r=1,调整因子。在智能体的状态演化过程中系统拓扑不能始终保持连通,经过约50次迭代后,11个智能体的状态值分裂成两个集群,分别是点0.9和点3.4,具体情况如图5所示。
6.一致性协议(4):11个智能体的状态值随机分布在[0,5]的区间内,通信半径r=1。在智能体的状态演化过程中系统拓扑始终保持连通,经过约15次迭代后,11个智能体的状态值达成一致,汇聚在一个点2.5上,具体情况如图6所示。
7.一致性协议(3):20个智能体的状态值随机分布在[0,10]的区间内,通信半径r=11,调整因子。在智能体的状态演化过程中系统拓扑不能始终保持连通,经过约80次迭代后,20个智能体的状态值分裂成四个集群,分别是点1.3,点3.2,点5.8和点8,具体情况如图7所示。
8.一致性协议(4):20个智能体的状态值随机分布在[0,10]的区间内,通信半径r=1。在智能体的状态演化过程中系统拓扑始终保持连通,经过约50次迭代后,20个智能体的状态值达成一致,汇聚在一个点4.8上,具体情况如图8所示。
通过以上仿真,可以观察到,当系统的初始拓扑是随机分布时,系统拓扑可能不能始终保持连通性,因而会分裂成多个集群。而在本文提出的一致性协议(4)下,无论系统的初始拓扑是均匀分布还是随机分布,系统拓扑在智能体的状态演化过程中一定能保持连通,并且各智能体的状态值一定能渐近收敛到初始时刻的全局几何中心,即达成一致性。而且,由于智能体的邻域选取策略是选择两个与自身状态差值最远(而非最近)的邻居智能体,系统的收敛速度明显加快。
4 结束语
在本文中,我们针对通信范围有限的多智能体系统,提出了一种离散时间一致性协议。在一维情形下,对于任意初始时刻连通的初始拓扑,基于该协议,智能体都能保持连通性,并一定能渐近收敛到它们的初始状态平均值。
我们未来的工作是设计一个更好的切换拓扑下的离散时间一致性协议。有三点值得进一步研究:
(1)寻找更好的方法来保持切换拓扑的连通性;
(2)设计更简洁合理的一致性协议;
(3)更快的收敛速度。

图5:协议(3)下初始拓扑随机分布在区间[0,5]的演化过程
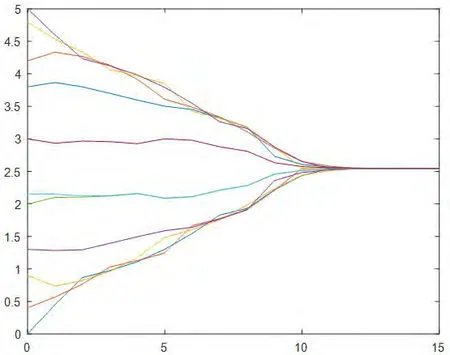
图6:协议(4)下初始拓扑随机分布在区间[0,5]的演化过程
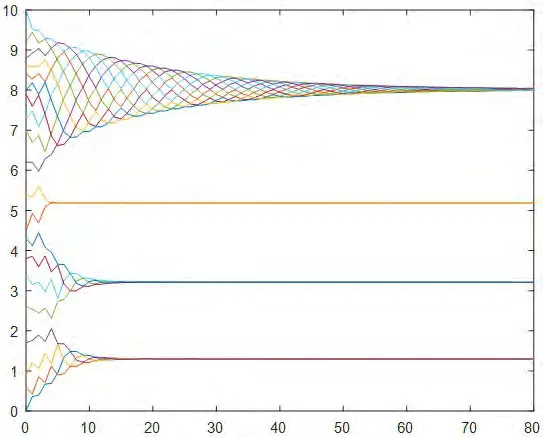
图7:协议(3)下初始拓扑随机分布在区间[0,10]的演化过程
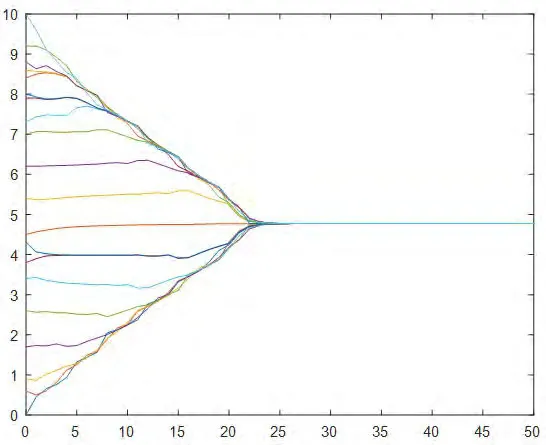
图8:协议(4)下初始拓扑随机分布在区间[0,10]的演化过程
