培养几何直观能力 发展数学核心素养

俞丹锋

摘要：数学是一门研究空间形式与数量关系的基础学科，是脱离具体事物的抽象化的知识。在数学教学中培养学生几何直观能力，能帮助学生将抽象的逻辑较强的数学问题利用图形直观化、具体化、简单化。教师在数学教学中要转变教学观念，注重学生直观感知，积极渗透数形结合思想，强化学生画图技能，加强实践操作，运用现代化教学技术，培养学生的几何直观能力，发展学生的数学核心素养。

关键词：数学教学；几何直观；核心素养；能力培养

中图分类号：G421；G623.5文献标志码：A文章编号：1008-3561（2022）14-0067-03

到了小学中高年级，学生的数学学习常常出现较为突出的两极分化现象，究其原因，是数学知识的抽象程度随学段的提高而加深。对不同年级数学教材进行对比，可以发现低年级的教材中例题和练习配套的直观图形较多，中年级教材中配套的图形明显减少，高年级知识以及练习呈现主要以文字说明为主。面对纯文字、没有配套直观图形的练习，学生感到理解题意比较困难。因此，在小学中高年级培养学生几何直观能力的重要性就凸显出来。在小学阶段培养学生的几何直观能力，教师可以从以下几个方面着手。

一、转变教师教学观念，重视几何直观能力培养

《义务教育数学课程标准（2011年版）》提出几何直观以后，很多教师认为培养学生的几何直观能力非常有必要，但在教学中却常常出现一些问题，主要表现在以下几个方面。首先，教师对“几何直观”的理解不够全面，认为几何直观能力只能在与几何相关的题型的教学中才能进行培养，这是一种片面的认识。实际上，在“数与代数”“统计与概率”“综合与实践”这几个知识领域都涉及几何直观。其次，部分教师在教学过程中重知识讲解，轻能力培养，导致学生的几何直观能力培养不足。部分教师为了学生成绩的提高对学生进行了大量练习以提高学生对知识点的运用能力，这样的教学导致学生只能就题论题，举一反三的能力相对薄弱。

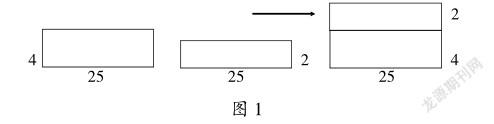
例如，在教学乘法分配律a×（b+c）=ab+ac时，部分教师让学生记忆公式或者利用诸如“我爱爸爸和妈妈等于我爱爸爸和我爱妈妈”之类的口诀方便学生记忆，这就是只重知识讲解的教学方式。学生只会套用，当题目变化后就不会灵活的应用，原因在于没有理解乘法分配律的内涵。对于四年级的学生来说，理解乘法分配律a×（b+c）=ab+ac这样抽象的知识点有一定困难。因此，教师在教学例题4×25+2×25=（4+2）×25的时候，除了从乘法的意义方面进行讲解，还可以把乘法分配律转化为图形的面积帮助学生理解（见图1）。教师可以引导学生把例题看成求长相同、宽不同的两个长方形的面积和。直观的图形可以给学生留下深刻的印象，使学生明白乘法分配律可以借助长方形的面积来理解，加深对乘法分配律的理解。

教师要改变传统的教学观念，以培养能力为导向，准确定位自身在课堂上角色，成为学生学习的“引路人”，给学生大胆发言的机会，让学生充分讨论，在学生遇到困难时适时指点，逐步提高学生解决问题的能力。

二、注重学生直观感知，让学生亲历几何直观过程

在小学阶段，学生的数学思维以形象思维为主，并逐步向抽象思维过渡。在这个阶段，教师要根据学生的认知规律，让学生多角度感知，逐步發展学生的几何直观能力。只有让学生多经历、多感知，才能将抽象的问题直观化。例如，“排队问题”对学生来说就非常抽象。对于“小明的前面有4个小朋友在排队拍照，他的后面有3个小朋友，一共有几个小朋友在排队”这个问题，教师可以先让学生现场模拟排队，形成直观感性的认识，知道共有8人排队。然后，教师可以在黑板上画出“○○○○▲○○○”这样的图形，引导学生说说图形的意思。学生根据刚才的排队活动，能轻松地理解4+3+1=8，并真正理解“1”的由来，明白可以用画示意图的方法解决类似问题。通过现场排队、画示意图等方法，学生在直观感知中经历了“文字→实物→图像→总结”这样的学习过程，将抽象的数学问题变为直观的图像问题，提高了几何直观能力。

三、渗透数形结合思想，提升学生几何直观意识

图形是抽象数学问题与直观认识之间联系的桥梁，在解决抽象的问题中发挥至关重要的作用。数形结合能把抽象的数量关系与图形有机地联系在一起，提供解决问题的思路。例如，在竖式计算的教学中，教师可运用数形结合帮助学生理解算理。如对于“16×3”，教师可以借助摆小棒的方法教学，16可以看成10根小棒（即一捆）和6根小棒，16×3是10根小棒和6根小棒加在一起的3倍，或者先计算单根的部分6×3=18（根），满10根变成1捆还有8根，再算10的3倍就是30即3捆，加上1捆和8根，合起来即48根。结合直观的实物或者图形可以让学生更好地理解算理，明确6×3为什么要向十位进1，降低学生的理解难度。

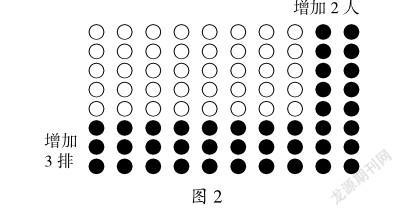
数学学习过程中，一些学生容易受到片面的直观认识的影响，陷入先入为主的错误中不能自拔，而数形结合能让学生更容易走出认识误区。例题：三年段组织学生参加队列比赛，每排有8人，共5排，现因队形变换需要，要增加3排，且每排增加2人，共需要增加学生多少人？一些学生认为增加了2×3=6（人）。如果教师不借助图形配合讲解，就无法讲清题中增加的人数到底在哪个部分，学生理解起来就非常吃力，而利用图形就十分容易纠正这种认识上的错误。学生从图2中就能直观地看到白色的圆圈表示的是原来的人数，需要增加的人数就是黑色部分，即（8+2）×（5+3）-8×5=40（人）。学生可以很容易看出来2×3仅是增加的一部分，从而突破理解障碍。