地下水渗流场对库区滑坡稳定性影响的数值模拟——以白马库区羊角滩滑坡为例

田 凯， 姚品品， 铁永波， 徐 伟

(1.中国地质调查局成都地质调查中心，四川 成都 610081; 2.中国地质大学(武汉)工程学院工程学院，湖北 武汉 430070)

0 引言

降雨入渗与水库蓄水引起库水位的抬升及水库调度，导致库水位大幅度升降，使水库沿岸岸坡地下水渗流场发生重大改变，是水库滑坡等地质灾害发生的主要诱因[1]。降雨入渗导致水库岸坡地下水渗流场变化的数值模拟问题本身就是水文地质工程地质的难题，而水库蓄水引起库水位的抬升及水库调度导致库水位大幅度升降使这一难题更加复杂[2-3]。因此，模拟降雨入渗与水库蓄水引起库水位的抬升及水库调度导致库水位大幅度升降联合作用下的滑坡地下水渗流场，成为当前水文地质工程地质界研究的一个热点内容[4]。

地下水渗流场数值模拟的主要任务是求解水头函数，确定渗流自由面和渗流量等渗流状态，其方法主要有有限单元法、边界元法和有限差分法[5-6]。用有限元方法分析地下水渗流问题时，若计算涉及到渗流自由面以及溢出面情况，由于渗流自由面(浸润线)所处的位置事先不确定，渗流流域范围便具有不确定性，这将导致边值问题中具有未定的边界，使得求解地下水渗流场问题由原本一个简单的线性问题变成事先部分边界条件不确定的复杂边界线性问题[7-9]。本文主要方法是通过迭代运算不断修改渗流自由面的位置，直至计算结果满足渗流自由面上的边界条件，获得足够接近实际情况的解答，最终确定渗流自由面位置，计算工作量很大是这种通过多次迭代运算最终确定自由面位置方法的明显缺陷[10]。

本文以重庆乌江白马库区上游羊角滩滑坡为例，结合区域水文地质工程地质资料[8]，通过调查试验得到模拟计算所需参数，从饱和/非饱和渗流的基本理论出发，讨论了渗流模拟有限元法的基本原理，给出了降雨入渗与水库水位升降联合作用下的渗流控制方程及有限元求解方法，利用Geostudio软件SEEP模块建立水文地质结构概念模型进行模拟，并对模拟结果进行分析，为今后类似工程实际应用提供一定的参考依据。

1 研究区概况

羊角滩滑坡位于重庆市武隆区白马镇乌江白马库区上游，库区白马航电枢纽工程已于2019年正式开工建设，滑坡位于该枢纽工程上游6.7 km，其稳定性直接影响着白马航电枢纽工程的修建(图1)。因此，本文选取羊角滩滑坡进行降雨和库水位变化条件下的地下水渗流场模拟分析，对滑坡稳定性进行定量评价。

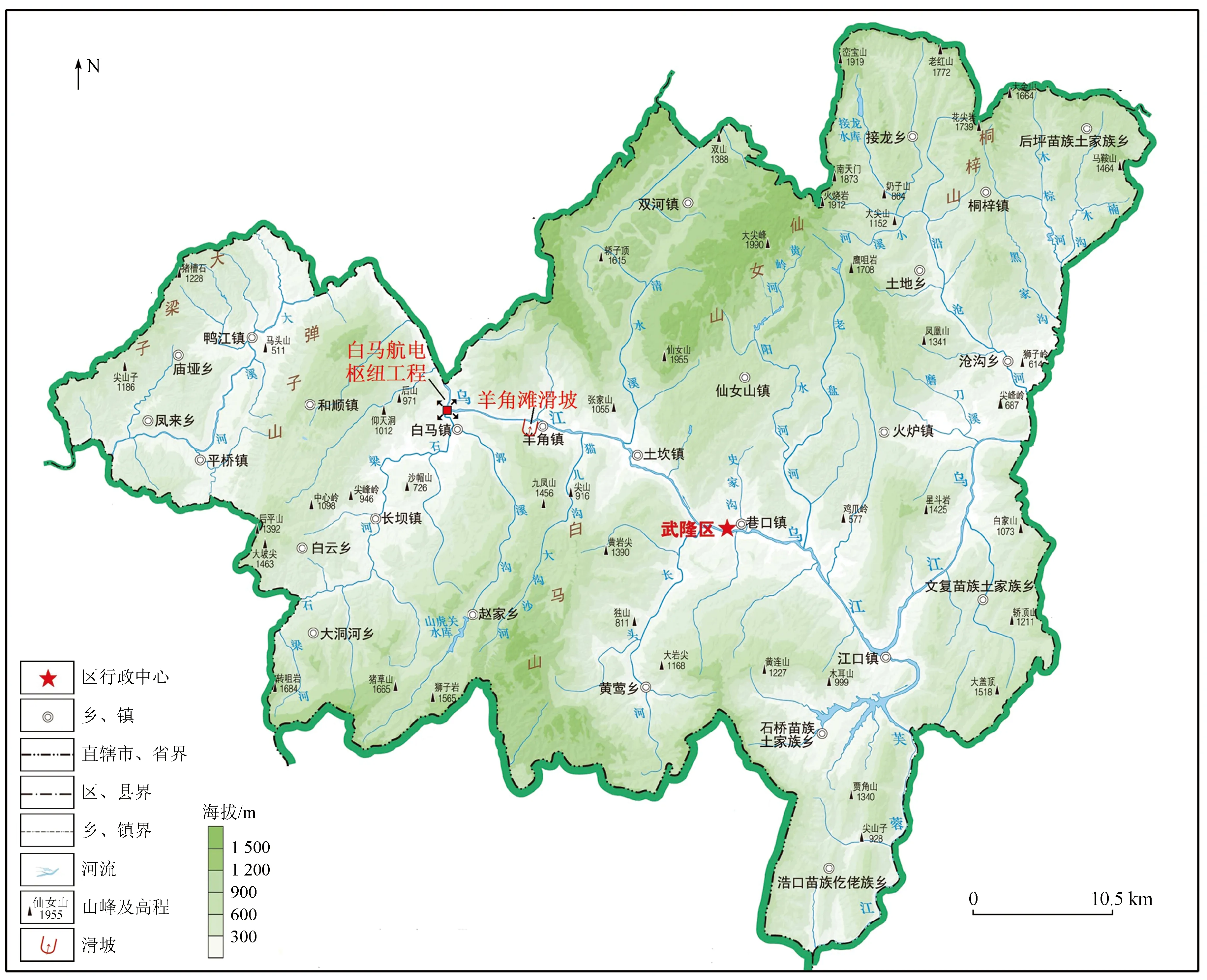
图1 羊角滩滑坡区域位置

羊角滩滑坡平面呈长舌形，主滑方向NE14°，后缘高程367 m，前缘高程159 m，纵向长1 066 m，平均宽372 m(后缘最小宽度51 m，前缘最大宽度541 m)，面积33.9×104m2，平均厚度19.9 m，体积672×104m3(图2)。据该滑坡的长期水文监测资料，库水位变化对滑坡后缘影响较小，因此选取滑坡距乌江0～725 m的范围进行模拟。图3为滑坡地质剖面。

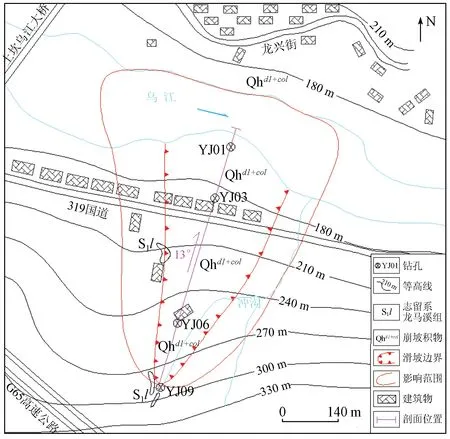
图2 羊角滩滑坡地质简图

通过已有勘查资料进行斜坡地质分层： ①分布于滑坡上部的崩坡积层(Qhdl+col)，主要成分为灰岩碎块石土，最大厚度约41 m； ②分布于滑坡体内部的滑坡堆积层(Qhdel)，主要为黏土夹少量碎石，最大厚度29.5 m； ③滑坡前缘分布于滑坡剪出口外侧河漫滩，为河流冲积堆积(Qhal+dl)，成分以粉细砂为主，细—中粒结构，较松散； ④发育志留系下统龙马溪组(S1l)浅黄、灰绿色砂质页岩。YJ01为钻孔，YJ03 、YJ06、YJ09为水文长期观测孔。

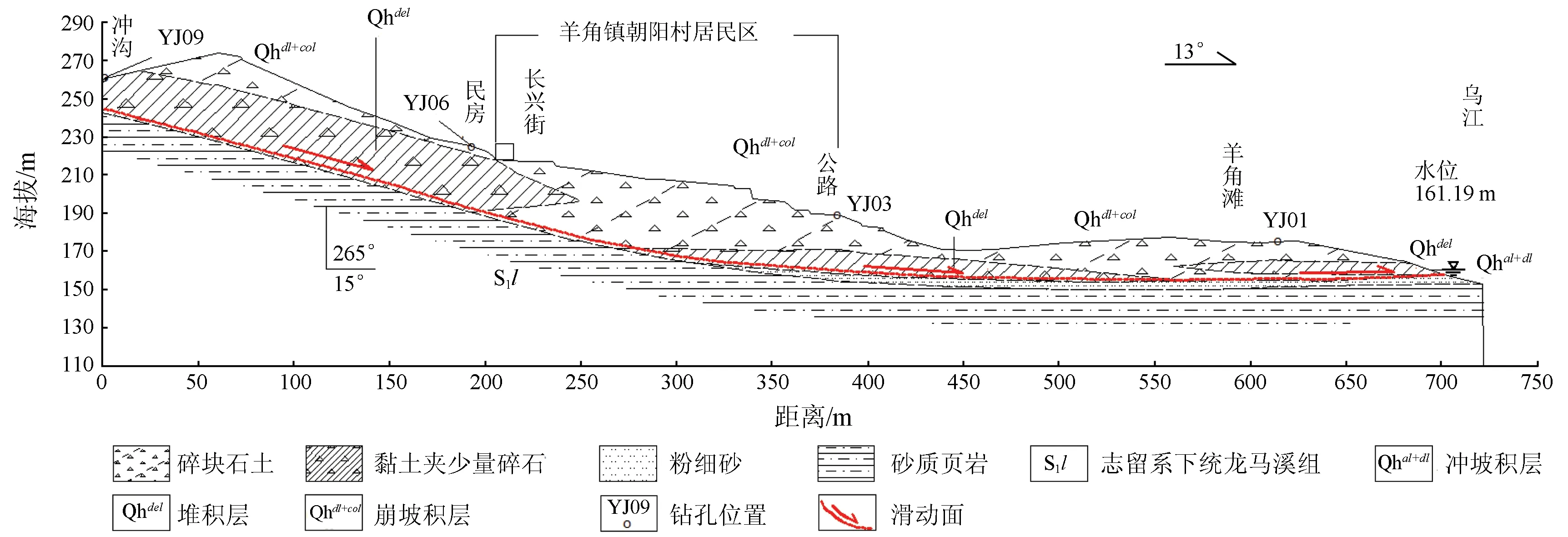
图3 滑坡地质剖面

2 滑坡计算模型的建立

本滑坡的剖分是根据具体边界条件，在满足一定精度要求的情况上进行的细致剖分，其中滑体的剖分较详细，而滑床的剖分较稀疏。滑坡建模及有限元网格剖分见图4,斜坡地质剖面分为4层。

(1)滑体表部中等渗透带。位于滑坡中部的坡体内部，为滑体表部强渗透带内的透镜体，下接弱渗透的黏土层，岩土体渗透性一般。

图4 滑坡模型的材料分区

(2)滑体下部弱渗透带。为后期形成的羊角滩滑坡的次级滑动带，位于滑坡的前缘，分布范围为海拔175～255 m，以类似透镜体的形式位于滑体下部。弱渗透带北端为滑坡前缘的剪出口，南端与滑体表部中等渗透带相连接，下伏基岩为滑床。岩土体的渗透性较差。

(3)滑坡前缘的强渗透带。分布于滑坡剪出口外侧河漫滩，为河流冲积堆积层，成分以粉细砂为主，层薄，下伏基岩，斜坡地下水主要通过该层向乌江进行排泄，地下水埋深相对较浅。

(4)基岩(不透水层)。表1为各个地层渗流模拟岩土体的饱和渗透系数。

表1 渗流模拟岩土体饱和渗透系数取值

2.1 初始条件和边界条件

在计算降雨前滑坡体的地下水位线时，首先需要根据勘察资料确定出初始水位。当乌江水位为161 m时，滑坡后部地下水位线倾角为9°，由此可以反算出滑坡左边界的水头边界为249 m。因此，在降雨前可以设定初始条件： 滑坡体左边界为249 m水头边界，滑坡右侧为乌江水位。然后，再模拟计算滑坡体降雨入渗期间引起的瞬态渗流及地下水位变化，通过在滑坡表面SEEP中定义边界函数来模拟降雨过程。

(1)入渗边界。假设降雨区域覆盖滑坡体表面，通过函数定义为单元流量边界。通过设计单位节点流量—时间的函数来确定降雨的大小和时间，通过定义某一时刻的单元流量来实现降雨强度的变化，动态模拟降雨入渗的过程。

(2)模型两侧。在滑坡右侧按定水头边界条件确定水位高程，左侧也按定水头边界条件水位高程。

(3)模型底面。假设滑床基岩的渗透性很小，滑床底部的边界条件可以设为不透水的边界条件。

2.2 模型参数的选取

根据Geostudio软件SEEP/W自带的函数，用土水特征曲线来研究非饱和土的含水率和土体基质吸力的关系，依据软件提供的土的渗透性函数来定义非饱和土的渗透性。在各种工况下，所研究滑坡共有3种岩土类型，所以选择碎块石土、黏土、粉细砂3种土的特性函数。本文选用Fredlund&Xing方法函数。根据现场地表注水试验和钻孔注水实验结果，可以得到模拟区域3种材料的土-水特征曲线及渗透函数曲线(图5)。

(a) 滑体碎块石土

(b) 滑体下部黏土

(c) 滑体前缘粉细砂

3 数值计算结果分析

3.1 模拟工况

选取YJ1、YJ3 、YJ6、YJ9为观测孔，与正常水位工况模拟计算结果作对比，然后逐步调整各渗透带的水文地质参数，直至满足模拟精度为止。据重庆武隆1951～2018年实测降水量资料统计，历年最大日降水量为157.54 mm(2003年6月24日)，以此作为特殊暴雨工况。根据水库实际营运条件，滑坡渗流计算采取下列6种计算工况。

(1)工况1。当前天然161 m河水位，该工况下前缘库水位为161 m，水位线下边界为固定水头边界，水位线以下为零水头边界，后缘为249 m水头边界，基岩面为零流量边界。

(2)工况2。暴雨、久雨+161 m河水工况(以161 m河水位为初始，降雨4 d)，该工况下前缘库水位为161 m，水位线下边界为固定水头边界，水位线以下为零水头边界，后缘为249 m水头边界，基岩面为零流量边界，上表面库水位线以上为降雨边界。

(3)工况3。183 m正常库水位工况，该工况下前缘库水位为183 m，水位线下边界为固定水头边界，水位线以下为零水头边界，后缘为249 m水头边界，基岩面为零流量边界。

(4)工况4。暴雨、久雨+193 m洪水位工况(以193 m河水位为初始，降雨4 d)，该工况下前缘库水位为193 m，水位线下边界为固定水头边界，水位线以下为零水头边界，后缘为249 m水头边界，基岩面为零流量边界，上表面水位线以上为降雨边界。

(5)工况5。182 m水位升至193 m洪水位工况(以182 m河水位为初始，4 d后升至193 m)，该工况为暴雨情况下，库水位在4 d时间内从183 m洪水位降至182 m水库正常蓄水位。

(6)工况6。193 m洪水位骤降至183 m水位工况(以193 m河水位为初始，4 d后降至183 m)，该工况为库水位在4 d时间内从193 m洪水位降至183 m水库正常蓄水位。

本文主要研究的是降雨和库水位这2个因素对滑坡地下水渗流的影响。通过对模拟结果的分析可知，库水位变化主要影响滑坡前缘，库水位的高低控制着地下水位的高低，库水位的升降控制着地下水位的升降，且地下水位是随库水位变化而迅速发生变化的； 降雨对整个滑坡的水位变化都有一定的影响，而且滑坡中部地下水位变化影响趋于最大，前后部影响趋于较小。

滑坡地下水渗流场的变化会引起其稳定性系数的变化，通过利用地下水渗流场模拟的结果得出最危险滑动面，用毕肖普法对羊角滩滑坡稳定性进行了简单计算，并分析渗流场变化对滑坡稳定性的影响。物理力学参数选取见表2。

表2 滑坡岩土物理力学参数综合建议值

3.2 模拟结果分析

采用毕晓普法进行计算，只考虑地下水位的不同对滑坡稳定性的影响。经计算，稳定性系数计算结果见表3和图6。

表3 各工况稳定性计算结果

(a) 工况1(稳定性系数=1.410) (b) 工况2(稳定性系数=1.222)

(c) 工况3(稳定性系数=1.274) (d) 工况4(稳定性系数=1.225)

(e) 工况5(稳定性系数=1.275) (f) 工况6(稳定性系数=1.158)

图6 不同工况条件下最危险滑面及稳定性系数

通过对表3和图6的分析，可以得出以下结论。

(1)不同库水位对滑坡稳定性的影响不同，随着库水位的上涨，滑坡稳定性系数呈现先减小后增大的趋势。分析其原因，是因为滑坡稳定性的变化主要受到浮托作用、压坡作用和渗流力作用的影响。该实例中，库水位的变化主要对滑坡前缘影响较大，前缘为阻滑段，当上部土层重力越大时，抗滑力与下滑力的差值越大，阻滑作用越强，滑坡越稳定。库水位变化对滑坡稳定性的影响正是通过这种方式进行的。初始阶段，随水库库水位的上升，水面以下土层比例将增大，水的浮托作用同比增大，在计算公式中体现为滑面反力减小，阻滑作用力降低，滑坡稳定性趋于减小； 当达到一个特定值后，如果库水位继续增加，库水便会起到一定的压坡作用，使阻滑作用得到增强，滑坡的稳定性将会增加。同时，水库库水位的上升还会减小滑坡中的水力的梯度值，使地下水渗流力趋于减小，有利于滑坡的稳定性。

(2)在降雨条件下，滑坡稳定性随着降雨历时的增加而趋于变小，到达一定阶段后，滑坡稳定性系数不再变化。本文对161 m水位(工况2)和193 m水位(工况4)进行了历时4 d的稳定性计算。由表3(工况2和工况4)结果可以看出，初始阶段稳定性系数减小幅度不大，随着降雨时间的增加，稳定系数将迅速减小，之后慢慢地趋于稳定。分析其原因是： 降雨入渗补给地下水需要一定的时间，当降雨入渗补给地下水时，水面上升，地下水渗流速度加大，滑坡的稳定性将迅速降低，之后地下水渗流情况趋于稳定，稳定性系数也就不再发生变化。

(3)库水位从183 m上升到193 m的过程中，随着库水位的上涨，滑坡的稳定性有所增加。分析其原因是： 183 m水位时，滑坡前缘阻滑段已经被库水淹没，而随着水位上涨，浮托作用将不再增大，而压坡作用却不断增大，同比水位的抬升，滑坡内水力梯度趋于减小，渗流力趋于减小，接近库岸处的部位甚至出现水体的倒流； 这些因素都会使得滑坡稳定性有所增大。

(4)库水位从193 m下降至183 m的过程中，滑坡的稳定性明显趋于减小。分析其原因是： 水库水位下降时，水库水压坡作用趋于减小，同时滑体内水力梯度增大，渗流力逐渐增大； 这些因素都将导致滑坡的稳定性变差，因此滑坡稳定性迅速趋于减小。

4 结论

本文对6种工况进行了数值模拟，并在模拟基础上对滑坡的稳定性进行了分析，得到的主要结论如下：

(1)该滑坡最危险潜在滑动面位置受地形地貌的影响较大，各种工况下，范围和位置变化相对较小。

(2)不同的水位情况下，随着降雨时间的增加，滑坡稳定性逐渐趋于减小，最后趋于一个定值; 降雨入渗需要一定量的时间，因此最开始滑坡稳定性减小相对较小。

(3)随着库区水位的升高，滑坡稳定性趋于减小，当水位到达一定值的时候，滑坡稳定性将随着水库的水位升高而趋于增大。

(4)地下水位的骤升对滑坡稳定性的影响要视具体情况而定。地下水位的骤升对浮托作用并没有太大影响，但对压坡作用影响比较大，同时降低了地下水渗流力的影响，因此，地下水位骤升不仅没有使滑坡失稳的可能性进一步增大，反而对滑坡稳定起到了积极的作用。

(5)当地下水骤降时，滑坡稳定性系数趋于最小。地下水位的骤降增大了其渗流力，降低了前缘库水位的压坡作用，但并未减弱地下水本身的浮托作用，因此在此工况下，滑坡失稳的可能性趋于最大。