基于ANSYS的混凝土重力坝坝基稳态渗流研究
2022-02-23陈驰
陈驰
(重庆腾云工程咨询有限公司,重庆400074)
0 引言
近年来,随着对水资源的不断开发利用,我国在长期的水利工程建设中积累了丰富的经验,水利事业也得到了蓬勃发展。特别是在建国以来,数以万计的水库大坝得以修建,对人民生活水平和工农业生产等都带来了巨大的收益。由于这些水利工程都是在不同时期建立的,基于修建时经济基础、技术水平、规划设计水平等限制,或多或少会出现一些质量缺陷,渗流问题就是其中之一[1]。渗流是指流体通过多孔介质的流动,在水利工程大坝运行中的渗流问题有坝体和坝基渗流作用所造成的渗透变形、滑坡及冲蚀等破坏,严重的甚至会影响大坝的安全稳定,对人民生命财产安全和国家安定带来难以预计的损害。因此,渗流分析是水工设计中不可或缺的一部分,工程实践表明,水利工程能否安全、可靠运行,很大程度上取决于能否正确进行渗流分析和选择合理的防渗措施[2]。
1 渗流基本理论
渗流现象普遍存在于自然界中,渗流理论也已经成为人类开发地下水、地热石油、天然气、煤炭与煤层气等诸多地下资源的重要理论基础。早在1856年,法国工程师Darcy通过渗透试验得到了渗流量Q与横截面A及水头差(H1-H2)成正比,与渗透路径L成反比的规律,即:
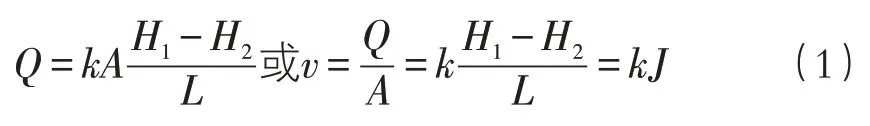
式中:Q——渗流量,m3/s;k——渗透系数,m/s;A——横截面积,m2;H1,H2——上、下游水深,m;v——流速,m/s;J——水力梯度。
上式称为Darcy定律[3],它指出了渗流速度v与水力梯度J或渗透阻力的线性关系,故又被称为线性渗透规律。Darcy定律描述的是层流状态下渗透速度与水头损失关系的规律,即渗透速度v与水力梯度J成线性关系只适用于层流范围,所以它的应用受到一定水力条件的限制[4]。渗透系数k,也称为水力传导系数,是一个重要的水文地质参数。它是表征多孔介质输运流体能力的性质(如粒度成分、颗粒排列、裂隙性质和发育程度等),而且和渗透液体的物理性质(重度和粘滞性)有关。渗透系数一般可在实验室和野外现场通过实验测定。
在水利工程中,渗流理论包括渗流的基本原理、渗流场的计算分析方法、土的渗透和渗透稳定性4个方面。土的组成物质、沉积条件及生成过程的多样性决定了其不均匀性。经过风与水的搬迁作用,多为松散的颗粒堆积,因而属于互相连通的多孔介质[5]。构成多孔介质的地质体在物质成分、颗粒大小、排列方式及后期改造作用等方面存在较大的差异,造成了多孔介质中空隙的几何形状、大小及方向的复杂性,决定了地下水在其中的运动是非常复杂的。
2 渗流数值模拟仿真基础
2.1 渗流自由面计算简介
许多水利工程中都存在着无压渗流问题,这类问题的关键在于求解渗流场的边界,即确定事先不知道其位置的自由面。它是岩土力学中的非线性问题之一,属于边界非线性问题[6]。按数值计算方法的类型,可将渗流自由面的计算方法分为有限差分法、边界元法、无网格法、有限元法。其中,有限元研究最多,应用也最为广泛,研究技术相对比较成熟。
2.2 渗流数学模型
根据渗流基本原理和基本方程,如图1所示的混凝土重力坝简化模型,当渗流方向与总体坐标轴一致时,可以得到其二维平面渗流场,其渗流基本微分方程[7,8]:

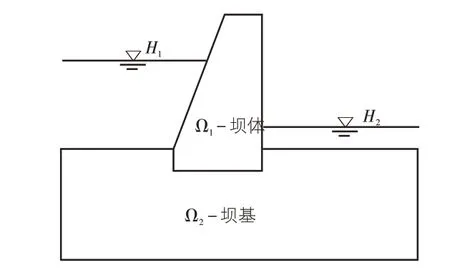
图1 大坝稳定渗流简化模型
式中:kx,ky——x,y方向的渗透系数,m/s;Q——内源;H(x,y)——坝体与坝基内的水头系数;H1,H2——上下游水位,m;n——单位外法向量。
根据变分原理,通过简化式可以得到,上述二维渗流问题就是求解下列泛函的极值问题。

3 混凝土坝数值模拟模型
3.1 计算结构模型
混凝土重力坝是依靠自身的重力来维持坝体稳定的,是一种经典实用的坝型。与其他建筑物不同,它的建设除了要考虑地基强度和变形等一般条件以外,还必须考虑水的渗漏问题。选取某水利枢纽中岩基上混凝土重力坝为研究对象,为了计算方便,数值计算例子的简化形状及尺寸如图2所示。大坝上游水位80m,下游水位20m。取河床中央垂直坝轴线的剖面为渗流场分析区域。坝基岩层取宽度为100m,渗流计算区域的长度取320m进行计算。
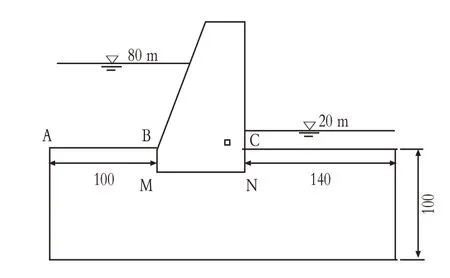
图2 大坝结构图
以上述算例进行有限元建模,直角坐标系建在坝踵位置处,X轴正向与水流方向一致,Y轴正向垂直向上,为了计算简便,不考虑非饱和渗流,仅考虑混凝土大坝下水的渗流。因此,可将将其简化为二维渗流问题,利用ANSYS稳态热传导进行分析。
3.2 材料参数
如前所述,混凝土大坝材料的各项参数如表1所示。
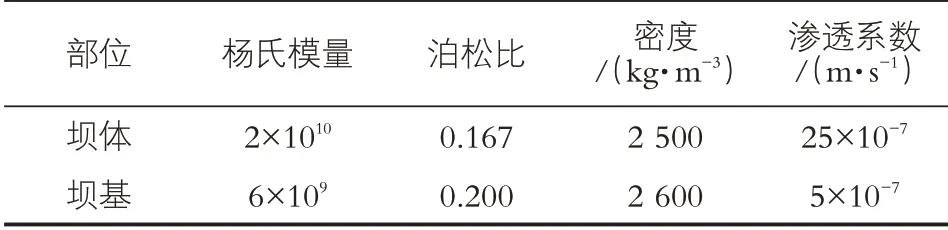
表1 各材料参数
3.3 边界条件
对于渗流而言,存在多种边界条件,包括流量、水头、流速等。这里为水头边界条件,上游水头为80m,下游水头为20m(在ANSYS中对应的为温度边界条件),对于不指定的边界默认为不透水边界(此算例中,假定模型左右两侧、底部及坝底为不透水边界)。添加边界后的有限元模型如图3所示。

图3 施加边界条件后的有限元模型图
3.4 计算结果
通过对有限元模型的求解,并通过ANSYS软件强大的后处理模块,得到了以下成功。计算模型的水头等值线分布云图如图4所示。
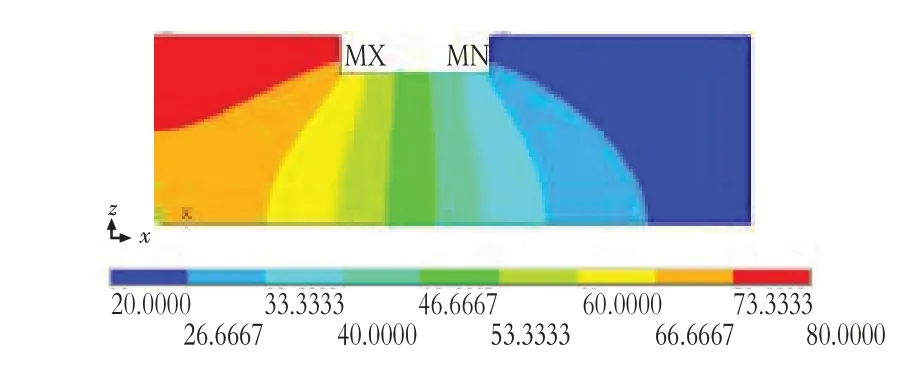
图4 水头等值线分布云图(单位:m)
渗流梯度等值线分布如图5(a),5(b),5(c)。
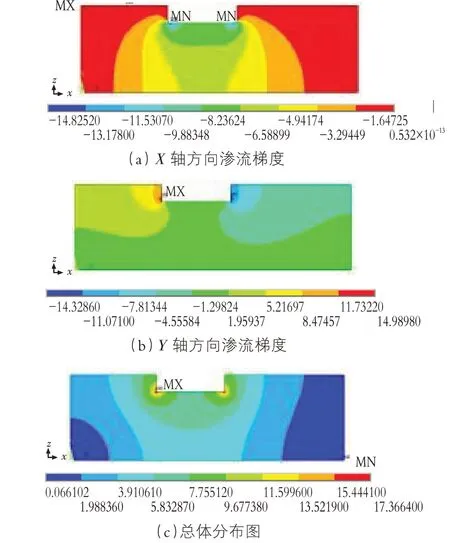
图5 等值线分布
渗流速度矢量分布如图6所示。
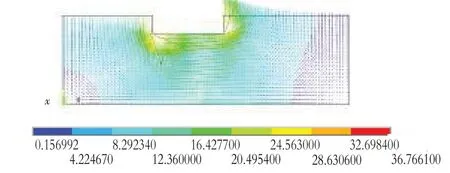
图6 渗流速度矢量分布示意图(单位:cm/s)
渗流速度沿指定路径的分布图如图7所示。
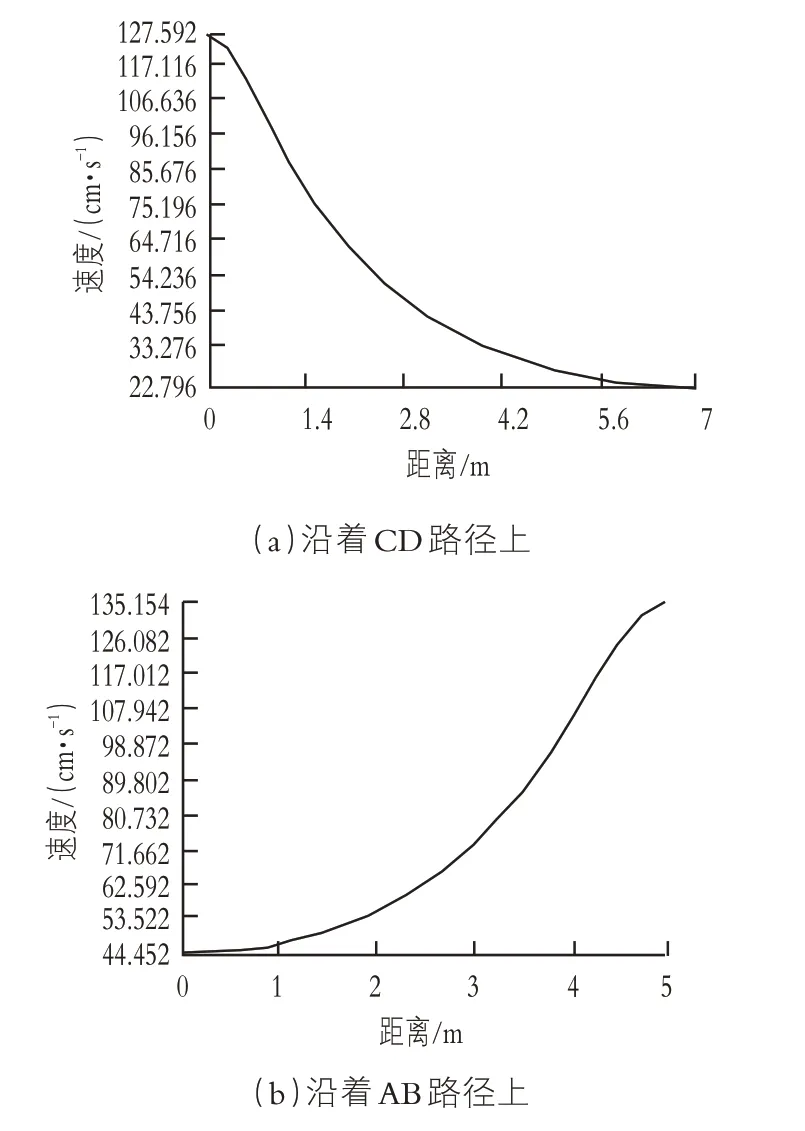
图7 渗流速度变化曲线
由计算结果可知:
1)从图4可以看出,水头沿上游到下游逐渐降低,且在靠近坝体的区域附近,水头降低的相对较快且分布区域集中。
2)观察图5可以看出,在X轴方向,处于坝踵和坝趾的M,N点处的渗流梯度最小,且从两点向外扩散的过程中,坝基区域渗流梯度不断增大,靠近边界处为最大。在Y轴方向,处在坝踵处的M点渗流梯度最大,而坝趾处N点则为最小,上游方向渗流梯度由M点向外不断减小,而下游方向渗流梯度则由N点向外不断增加。总体来看,M,N点附近仍是渗流梯度最大的区域,且从两边不断扩散的区域,渗流梯度呈递减趋势。
3)如图6所示,渗流均是由上游至下游逆时针方向。且同样是靠近混凝土重力坝坝踵和坝趾处渗流速度较大,并呈向外扩散递减趋势。
4)为了查看渗流速度具体变化趋势,指定两段路径:第一段为上游远离大坝的A点到上游坝踵处B点,第二段为下游坝趾C点到远离大坝的D点。由图7可知,从A点到B点渗流速度在不断增加,且增加的幅度越来越大,整体趋势大致呈抛物线分布,从C点到D点渗流速度在不断减小,且减小的幅度越来越小,这与图6中的规律是完全一致的。
4 结论
基于渗流基本理论、渗流数值模拟仿真基础及渗流数学模型,有限元分析很好地模拟了渗流分布规律。从计算结果可以看出水头等值线分布情况、渗流梯度及渗流速度分布规律。对于混凝土重力坝坝基的渗流,在坝体与坝基交界处的渗流作用较为明显,在远离坝体的区域渗流作用较小。因此,在工程实践中要特别注意采取防渗措施,以文中算例来讲,要特别关注交界面的渗透影响,采取合理的措施,保证结构的稳定安全。
