《圆的认识》教学设计
2022-09-02虢小鹏
文|虢小鹏
【教学内容】
北师大版小学六年级上册第一单元。
【教学重难点】
掌握圆的本质特征,归纳并理解半径和直径的关系,建立圆与直边图形之间的辩证关系。
【教学过程】
一、情境导入,揭题明标
1.复习:我们以前学过的平面图形有哪些?请你简单说说这些图形的特征?
长方形 正方形
平行四边形 三角形 梯形
2.这些图形都是用什么围成的?
3.今天我们来学习一种由曲线围成的图形,猜一猜是什么?
4.揭题:圆的认识。
二、合作交流,探究圆的本质特征
课前套圈游戏:请2 位学生玩套圈,初步感受套圈要“距离目标一样远”。
(一)设计“套圈游戏”方案,初步感受直边图形与圆之间的联系。

上面是一种“套圈游戏”,如何设计一个能同时让多名玩家(至少3 人)玩套圈,且对每个人都公平的游戏?
1.确定方案。
(1)先从最简单的3 个人开始设计,画出示意图。
(2)当人数增加到4 人、5 人、6 人……,设计怎样的图形更公平?
(3)研究的过程中你有什么发现和困惑?请记录下来。
(4)先独立完成,然后在小组内讨论,再完善自己的设计。
2.教师演示3 个人游戏。
(1)正三角形——3 个人。
①按照第一幅主题图来设计,这样公平吗?

预设:左右两边线段距离是相等的,但中间线段的距离和它们是不等的,所以这样的设计是不公平的。
②那应该怎样设计让3 个人玩起来公平?

预设:画出一个等边三角形,三个顶点到中心的距离是相等的,对于3 个人来说,这样的设计是公平的。
③追问:那是否一定要是“正三角形”才行呢?
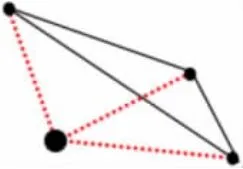
预设:也可以从小旗出发向不同方向量出3cm 后,将端点一次连接,形成一个不规则三角形(三个点的所在是一部分圆弧)。
3.小组合作,汇报交流
(1)怎样设计就可以保证游戏公平?组内分工,设计出4、5、6、7、8 人游戏方案。
预设:只要所有参加游戏的人到小旗的距离相等就行(到定点的距离相等)。
(2)正方形——4 个人。

①当人数增加到4 个人时,设计正方形,首先四个顶点分别站一个人,他们到对角线交点的距离是相等。
②也可以取四边的中点站人,到中心点之间距离也是相等。两者本质上没有区别,将人所站的点依次连接,还是一个正方形。
③按照刚才的方法,当人数增加到5、6、7 个人,设计的图形是怎样的?
预设:正五边形、正六边形、正七边形。
(3)正八边形——8 个人。

①预设:画一个正八边形,8个顶点上站人,到中心点的距离相等。
②正方形只有4 个顶点,是否只能站4 个人呢?
预设:可以将正方形每一条边平均分成3 份,这样一条边可以站2 个人,一共可以站8 个人,到中心点的距离都是相等的。
(二)建立直边图形与圆之间的联系,感悟圆的特征。
1.如果人数增加到9 人、10人……100 人呢?通过刚才的研究,你发现了什么?
预设:有多少人,就要设计“正几边形”。也就是人数一变,边数也要跟着变。
追问:你还愿意画吗?刚才我们所设计的图形局限性都很大,那能不能找到一个图形,适用于所有情况?
预设:圆,圆是没有顶点的,不是直边,圆上有无数个点,圆上的点到中心点之间的距离都是相等的。这样的设计,游戏就是公平的。
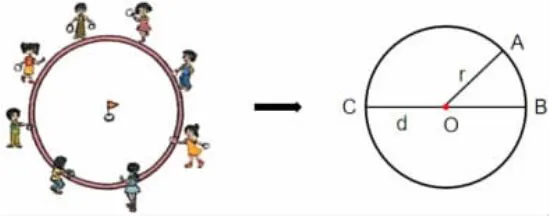
2.介绍圆的各部分名称
(1)各部分名称:点O 是圆心;连接圆心到圆上任意一点的线段叫半径,线段OA 是半径,通常用r 表示;通过圆心,且两端都在圆上的线段叫直径,线段BC 是直径,通常用d 表示。
(2)怎样理解“圆上”?“通过圆心”又是什么意思?
(3)通过我们设计的“套圈游戏”,再结合刚才新认识的圆,你认为在同一个圆内,半径和直径有什么特征?它们有什么关系?
3.小结:(1)在同一个圆里,有无数条直径,且所有的直径都相等;在同一个圆里,有无数条半径,且所有的半径都相等。
(三)自主画圆,加深对圆特征的理解。
1.不借助圆规你如何画圆?用圆形杯子盖等画出的圆,如何找到圆心?
2.用圆规画一个圆,并用O、R、D 标出它的圆心、半径和直径。
(1)为什么同学们画的圆不一样呢?(什么决定圆的大小?什么决定圆的位置?)
小结:半径决定圆的大小,圆心决定圆的位置。
(2)用“几何画板”软件小结出画圆的步骤和方法:定半径;定圆心;旋转一周。
强调:画圆时,圆规两脚间的距离不能改变,有针尖的一脚不能移动,旋转时要把重心放在有针尖的一脚。
三、巩固练习,拓展提升
(一)看图填空。
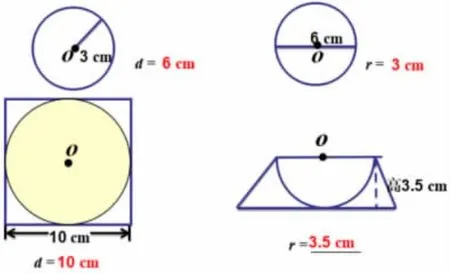
(二)车轮为什么是圆的?

(三)判断。
1.画圆时,圆规两脚间的距离是所画圆半径的长度。( )
2.两端都在圆上的线段,叫做直径。( )
3.圆心到圆上任意一点的距离都相等。( )
4.半径2 厘米的圆比直径3厘米的圆大。( )
5.所有圆的半径都相等。( )
四、介绍圆的历史
1.生活中你在哪里见过圆?
2.圆的历史。
3.“圆出于方”——渗透“无限分割”的思想,为圆的面积学习做铺垫。
