说理，追寻“知识之后”的学习

文|黄伟华

信息时代，几乎所有的事物都在以某种速度发生着变化，有的甚至是翻天覆地的，比如传递方式、人际交往等。可是回望我们的教育，本质上发生的变化却是微乎其微，这显然和快速发展的社会需求发生了某种冲突。基于数学这门学科，笔者思考，如果课堂仍然只是教给学生知识和技能，始终停留在学习的浅层目的，终将被时代的潮流所淹没，那绝对不是数学学习的最终方向。处在互联网时代的我们，已经迎来了最大的挑战——从“知识为本”转向“能力为本”“育人为本”，时代对人解决问题的能力要求越来越高。那么，数学教学该如何以知识为载体，处理好数学知识与育人之间的关系，帮助学生拥有应对未来挑战的素养？

带着这些思考，笔者琢磨《分数的基本性质》一课，反复斟酌课堂该如何帮助学生带着数学应有的理性视角，不仅与知识对话，更与知识说理，发起“知识之后是什么”的追问，从而实现对符号知识的超越和真正认知，在解决问题的过程中学会学习，获得精神上的成长。

一、思“理”——发展质疑的能力

在大多数情况下，只要知道问题是什么，就能想到多种多样的解决问题的方案。我们常常觉得学校教育培养出的问题解决者能力不足，与学生很少甚至没有机会自己去发现问题、去质疑有关。所以，就教学而言，我们需要的不是定义好问题，老师说问题是什么就是什么，而是站在学生的角度思考，关于这节课，学生真正的困惑是什么，启发学生叩问“知识背后的道理”，体会学习是从真问题开始的，发展质疑的能力、批判的能力。

细读《分数的基本性质》，所表达的“分数的大小不变”指的是一个分数的分子和分母同时乘或除以一个不为零的数，所得到的“另一个分数”与“原来的分数”是相等的。所以，这就涉及到“相等分数”这一问题。分数基本性质的数学价值也就在于揭示分数“表示形式的不唯一”和“等值”的本质。但在对已学过本课知识的学生进行调查的过程中，我们发现学生虽然知道分数的基本性质，却不了解这一概念背后的本质道理是什么，不能理解相等的分数中隐含着分数单位、分割、合并及单位量转换等概念。笔者思考，这与教师在教学中忽视等值分数的理解，而把学习的重点落在分子、分母的变化规律上有关。但事实上，学生只有在理解等值分数为什么相等的基础上才能真正理解分数的基本性质。

那么，关于本课，学生已经知道了什么？还有什么困惑？怎么使教学立足于学生的真问题？

基于以上思考，笔者对来自不同县区的三个班级学生做了学情前测，提出三个问题：

1.有相等的分数吗？如果有，请你举个例子，并说明理由。

2.仔细观察这几个分数，你发现了什么？

3.你有什么疑问吗？

前测结果显示，问题1 中，96.2%的学生知道有相等的分数，能举出等简单的例子来说明，并且能主动观察和发现，借助画图，从直观的角度或者文字等来说明相等的理由，但对其中隐含着的分数单位分割、合并等本质却难以自发发现。问题2 中，94.2%的学生能发现分子和分母发生变化，其中有一半的学生能发现分子和分母的变化规律。问题3 中，大部分学生都提了问题，其中有28.8%的学生提出了同一个问题：为什么分子和分母都不一样，但分数的大小却相等呢（如图1）？可见，虽然学生知道有相等的分数，能从画图直观得到相等的结果，却仍质疑分数相等的理由。

图1

在前测的基础上，教学立足于学生的已有经验和质疑，从学生举例的相等分数开始，并围绕学生的真问题，以“为什么分数的分子和分母都不一样，分数的大小却相等呢”为本课核心问题展开学习。既肯定学生质疑的能力，又激活学生已有的知识经验，触发学生对知识本质道理的思考与追寻，从而打开理性思维的窗口，真正的学习从这里拉开序幕。

我们知道，如果只看具体的知识，学生发现的问题就会浮于表面，思维探及不到深处，窥见不到本质。“你有什么疑问吗”这一问题，使得学生将知识重置，不再停留在表面符号的“是什么”，主动对知识发起质疑，产生追寻本质道理的好奇与欲望，叩问“是什么”背后的“为什么”。发展学生质疑能力的同时，启发学生意识到自己的认知存在着缺口，自觉寻求改变，产生打破知识桎梏、填补缺口的动力，想把知识的理解推得更深一些、更远一些，使学习真正发生。

二、析“理”——构建学习的方式

我们知道，解决问题的方法有很多种，但最有力最有效的那一个，一定是透过现象洞察本质的方法。继“为什么”之后，我们还应引领学生思考“怎么做”。启发学生主动剖开知识的表象，用自己的方式和知识讲道理，产生自己的思考，从不同角度来表达、来输出，和他人进行思维的碰撞交流，从而深入知识的本质，厘清问题的根源，提升解决问题的能力，构建起学习的认知方式。

教学尊重学生的现有经验，基于“为什么相等”这一困惑，借“想办法说明理由”将知识与学生的个人经验、思维方式联系起来，调动学生积极主动地开展探索性活动，使学生在独立思考中，迁移、运用原有的认知，从不同的角度来解释说理。静悄悄的思考过后，有的学生从部分与整体的关系分析（如图2），结合面积模型等画图的方法，提出虽然分的份数不同，但三个分数所代表的量是相等的；有的学生打通分数与除法的关系，将分数转化成除法，在计算中发现，通过计算证明其结果都相等，都是0.5；还有的学生借助上节课学习的分数墙（如图3），从测量的意义来理解，三个分数选取的分数单位虽然不同，但测量的值是相等的……基于不同的背景意义来理解，同样发现这三个分数形式不同，意义不同，但大小却相等的数学事实。

图2

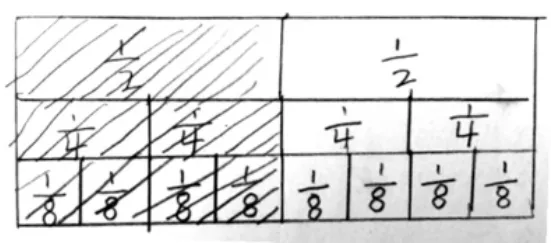
图3

“分数的大小没变，那变的是什么呢？这之间有什么联系吗？”“为什么分数的分子和分母同时乘或除以一个相同的数（零除外），分数的大小不变？”等追问，使得学生不断地超越已有的知识，进一步探索新出现的困惑，并再次从直观的角度，主动比较和发现，借助图示分析分数的分子和分母的变化规律是有道理的。在画图中展开交流辨析，在表达中与他人的思考链接起来，从均分或合并分数单位的角度上（如图4），体会把每一份继续平均分，原来1 个就被分割成2个、4 个；反之把份中的每2 小份、每4 小份进行合并，4 个就合并成了2 个、1 个。分数单位变了，表示的形式也就变了，但分数的大小不变。从直观到说理，从原来“部分——整体”的关系到分数单位的转换，从量的守恒到关系的守恒，突破变化规律的表象，逐步洞察等值分数的潜在道理，勾勒出分数基本性质的本质属性。

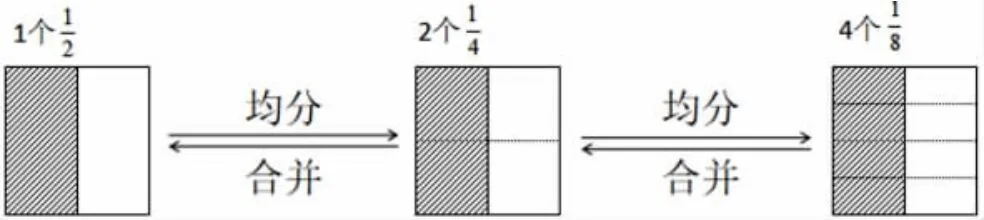
图4

人不可能独立于社会而存在，人是社会的人。正因为是社会的，所以不仅要拥有独立思考的能力，更要拥有表达的能力、与他人协作解决问题的能力。在以上的辨析说理活动中，学生不断地思考、表达与交流，不仅真正以自我生成的逻辑去理解、去经历、去构建自己的思维方式，更在解决问题、追溯知识原貌的过程中，体会学习不是孤立的、简单的输入储存，而是一种协作下的再经历、再创造的输出活动。在这个过程中，思维质量变得更高、迭代更快，也更理性、更本质地建立起知识的认知方式、问题的解决方式，拓宽认知视角的同时，丰厚了学习的社会性意义。

三、明“理”——完善认知的结构

知识与知识之间往往有着千丝万缕的关联，但教材为了教与学的实际需要，为了降低学习的难度，常将知识进行一些分割和细化。如此，学生头脑中的知识是零散无序的。所以，学习不能只是简单地将每次学到的知识进行堆积，还得洞察知识与知识之间的关联，从局部到整体，从知识结构的发展到思维结构的内化，促进理性思维的发展，使学习走向深入。

课的最后，教学立足于整体知识的结构之处，提出“今天学习分数的基本性质，感觉它熟悉吗”引发学生把研究的知识与已有商不变的规律横向关联。主动从分数与除法的角度沟通分数的基本性质与商不变的规律，在不断地回顾内涵、扩充外延中迁移生长，从整体上窥见概念间本质的联结，打通关联知识的阻隔，将看似散乱的概念有机融合，体会这二者虽形式上不同，但事实上是用不同的形式表示相同的规律。进一步感受分数基本性质合理性的同时，丰富概念理解的深度与维度，主动建构新的知识体系。继而思考“还能是什么？”“还有新的疑问吗？”使得思维的碰撞不断产生更多的联想，延伸思考，打开知识的纵向联系，将分数基本性质置身于日后的分数运算等不同情境或场合中，体会分数的应用不仅可以而且需要选择适当的“替身”，丰厚思维的同时，走向深度的学习。

从某个角度来说，学习就是在知识探寻与自我创造的过程之中，主动连接起碎片化的知识，沟通事物的内在联系，明晰知识的本质。在这个过程中，触发学生向下扎根，从局部知识看到整体知识，建构知识的结构；又向上生长，从知识结构的建构到思维结构的内化，从不同侧面完善对数学学习的认知，获得理性的智慧。

知识总有被遗忘的一天，而学习的过程却能使得各种新知不断被发现。“是什么”“为什么”“怎么做”这三个问题有着各自不同的价值，但“为什么”“怎么做”的知识对学生发展的价值越来越显得重要。所以，对数学教学而言，说理就似催化剂，启发学生不满足于知道知识“是什么”，更透过现象追究“为什么”，思考“怎么做”，不断催化学生的思维深度参与。“教知识”绝不是数学教育的全部价值，知识的真正价值应该在于育人，在于开发学生的思维品质与精神发育。数学教学只有直面学生的发展现实，启发学生在质疑中展开对知识本质道理的思考与辨析，方能洞悉知识的原貌，遇见“知识之后”的学习样态，帮助学生于再经历再创造的学习中，催生思维方式、认知方式、学习观念等逐节生长发育，获得素养的发展，实现知识学习真正的目的与价值。