枢纽拥堵状况下绿色多式联运路径选择不确定性研究

李立，黄理莹，牟玲玲

(河北工业大学 经济管理学院，天津 300401)

多式联运一定程度上缓解了经济发展与环境保护之间的矛盾[1]，同时使得运输过程的规模效应得以凸显，能大幅度降低运输成本。目前，多式联运在我国还处于发展阶段，呈持续增长态势，可以预计，未来枢纽处发生拥堵是普遍现象。一些学者尝试用排队论解决这类问题，将等待的货运流定义为花费时间在服务上的用户。RODRⅠ-GUEZ 等[2]将转运过程模拟为M/M/1 排队系统，根据排队模型计算拥堵成本并纳入枢纽选址模型中；MOHAMMADⅠ等[3]探究了枢纽拥堵对其选址问题的影响，并建模为M/M/C 排队系统；RAHⅠMⅠ等[4]研究了枢纽容量有限的拥堵问题，利用M/M/C/N模型计算等待时间；YU 等[5]使用排队模型模拟货物装卸过程中的拥堵状况，基于预测到达率评估了由于拥堵导致的排放；唐继孟等[6]将规模效应及拥堵效应的联动影响纳入公铁联运的枢纽选址分配模型中，利用M/M/C 模型描述枢纽处拥堵现象。可以看出，既往研究大多利用排队模型模拟枢纽处的拥堵现象，探究其对枢纽选址的影响，鲜少关注拥堵对于路径决策的影响。其次，多式联运运输过程复杂，参与方众多，且运输距离较长，因此易受多种外界因素影响，存在很大不确定性。一些学者使用随机规划，如期望值模型[7-8]、机会约束规划[9]，利用样本平均近似法[10-11]进行求解；一些学者使用模糊规划，利用模糊数表示不确定变量[12-15]。以上方法都是基于分布函数或模糊隶属度函数已知的前提下进行，但多式联运运输过程复杂，很难获取确切信息描述不确定变量，而鲁棒优化方法仅需给出不确定参数变化区间，便可根据决策者需求调节模型保守度，应用更为灵活，故本文使用基于不确定基数集的鲁棒优化方法解决运输中的不确定性。综上，本文利用排队模型得到由于拥堵产生的延误时间及排放，将其纳入路径选择模型；同时采用可调式的不确定集合表示运输时间，构建鲁棒优化模型，依据强对偶理论转化得到相应等价模型，并通过实际算例进行分析，探究枢纽拥堵现象对于绿色多式联运路径决策及排放的影响，寻求最优运输方案。

1 模型构建

1.1 问题描述

本文研究主题为多式联运的路径选择问题，货物由起点出发，通过由公路、铁路构成的运输网络G(M,A,K)运往目的地，其间经过若干转运枢纽，存在若干种运输方式选择，由于运输过程中存在诸多不确定因素，因此基于多式联运运输时间不确定的情况下，考虑枢纽拥堵对于多式联运路径决策及碳排放的影响，建立鲁棒优化模型，在此基础上，将低碳政策纳入模型中，综合考量经济效益及环境影响选择恰当的运输路径。

本问题假设如下：1) 每批货物在运输途中无法拆分，也即过程中货物总量不可增加或减少，保证运输订单完整性；2) 每批货物转运只发生在枢纽节点，且各节点处至多转运一次；3) 不考虑因外界环境因素造成的货损成本；4) 转运枢纽处集装箱到达的时间间隔服从泊松分布，平均转运时间服从指数分布。其中，问题中涉及参数符号及含义如下：

M为 运 输 网 络 节 点 集 合，i∈M,i=1,2,3,…,|M|，j∈M,j=1,2,3,…,|M|；A为 运 输 网络弧aij集合，i,j∈M；K为运输方式集合，k=1,2，其中1 为公路运输，2 为铁路运输；E为运输总成本，元；E1为直接运输总成本，元；E2为货物转运总成本，元；为运输方式为k时路段ij间的运输距离，km；Q为集装箱运输总量，t；为路段ij中货运方式为k的单位运输成本，元/(km·t)；为运输方式在节点i处由k转变为l 产生的单位成本，元/t；P为运输过程中产生的总排放，kg；P1为直接运输过程中产生的排放，kg；P2为转运过程中产生的排放，kg；为路段ij中货运方式为k产生的单位排放量，kg/km；为运输方式在节点i处由k转变为l 的排放系数，kg/t；为运输方式为k时在路段ij间花费的时间，h；为运输方式在节点i处由k转变为l 所需的时间，h/t；T为给定运输过程的总时间上限，h；r为征收碳税的执行税率，元/kg；决策变量：，选择运输方式k在路段ij间进行运输则取1，否则取0；，运输方式在节点i处由k转换为l 则取1，否则取0。

1.2 枢纽处拥堵现象模拟

1.2.1 拥堵时间计算

基于上文假设，此时多式联运枢纽处的转运过程可视为M/M/1 排队系统。其中，λi为节点i处单位时间内平均到达率，TEU/h；μi表示节点处单位时间系统的平均服务效率，TEU/h；Ni为节点i处服务系统的容量，TEU；ρi为节点i处枢纽的服务强度(ρ=λ/μ)；c为标箱与载重之间的换算系数。枢纽处平均排队时间Wqi及服务时间Wsi可计算如下：

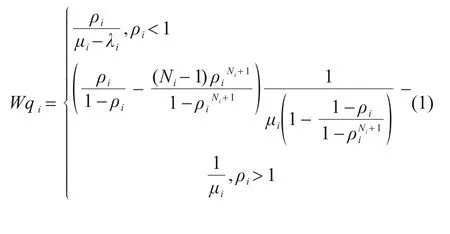
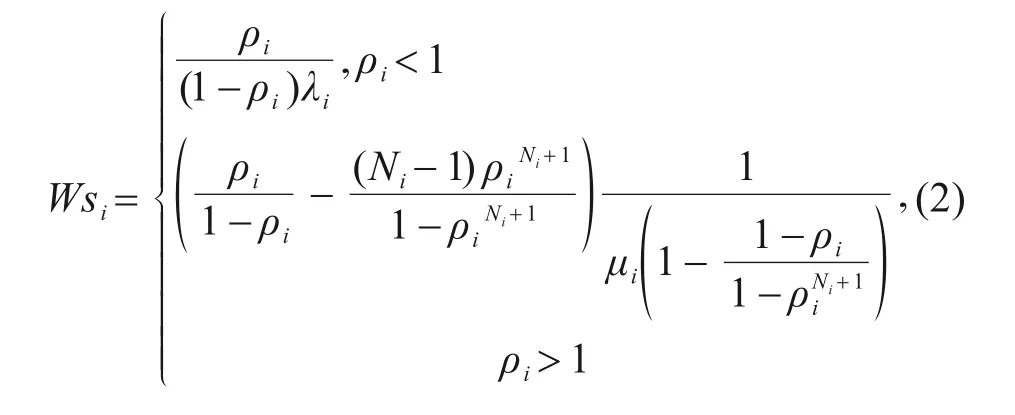
1.2.2 拥堵过程产生的排放

在考虑枢纽拥堵的情况下，转运枢纽处产生的排放可分为2部分：正常转运过程中的碳排放以及由于拥堵产生的额外碳排放。而在转运枢纽处，集装箱卡车是拥堵过程中最主要的排放源，这很大程度上是由于车辆长期处于怠速状态且在中转过程中走走停停，导致排放增加[5]。上文已经得到枢纽处的平均排队时间，假定集装箱卡车发动机状态相同，由此计算枢纽处因拥堵产生的排放量Pqi，E0为集装箱卡车怠速下的排放系数，如下所示：

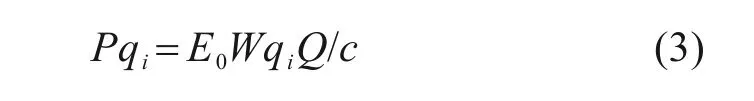
1.3 构建确定模型

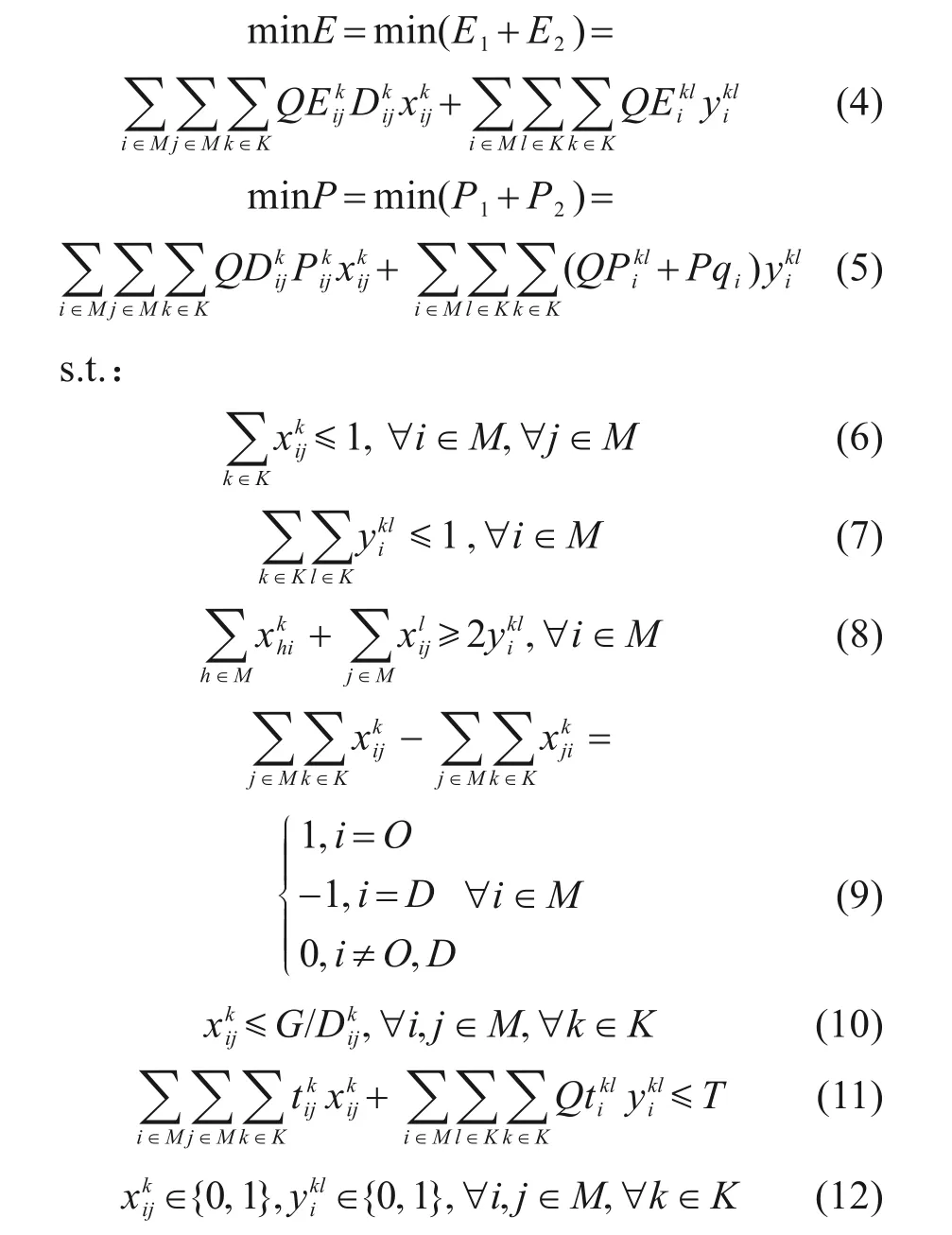
基于以上问题描述，将拥堵时间及等待过程中产生的排放纳入模型，以最小运输成本、最低碳排放为求解目标构建确定性路径选择模型。其中，式(4)和式(5)为目标函数，式(4)表示求解最低运输成本，由直接运输总成本与节点处的转运总成本构成；式(5)表示求解最小碳排放，由各路段排放之和与各节点转运过程产生的排放之和构成。约束(6)表示2个节点间至多选择一种运输形式。约束(7)确保货物在节点处的中转次数至多为一次。约束(8)为保持节点转换信息与节点路段前后运输方式的一致性。约束(9)确保了节点处货物量流入和流出的平衡。约束(10)确保节点间不存在该运输方式时，决策变量取0，G为足够小的正数。约束(11)确保运输任务总时间不超过给定上限。约束(12)表示决策变量为0-1变量。

2 绿色多式联运路径选择的鲁棒优化模型

基于上节已经建立的确定性模型，考虑多式联运运输时间不确定时的路径决策问题，而在已经给出的确定性模型中，其余参数确定，因此仅需针对不确定运输时间构建鲁棒优化模型。利用区间法表示不确定变量，将不确定的运输时间定义 为，其中，为运输时间均值，为扰动量。参考BERTSⅠMAS 等[16]针对区间鲁棒优化做出的改进方法，引入随机变量定义为对称且分布未知的随机变量，其不确定集合可定义为为不确定水平参数，决策者可以通过改变值灵活调节目标函数解的保守程度从而优化模型的鲁棒程度。综上，运输时间可以重新表述为，调整确定性模型的约束条件：

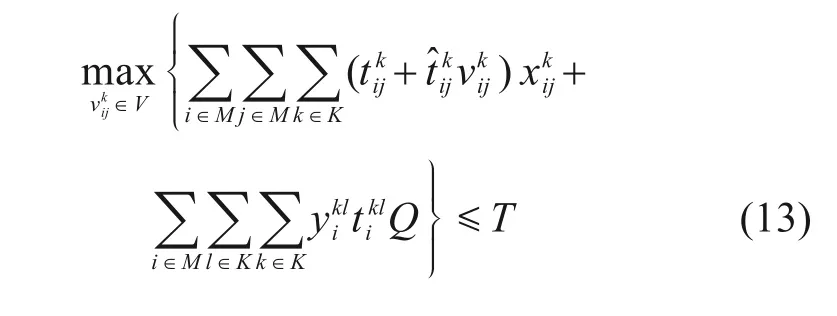
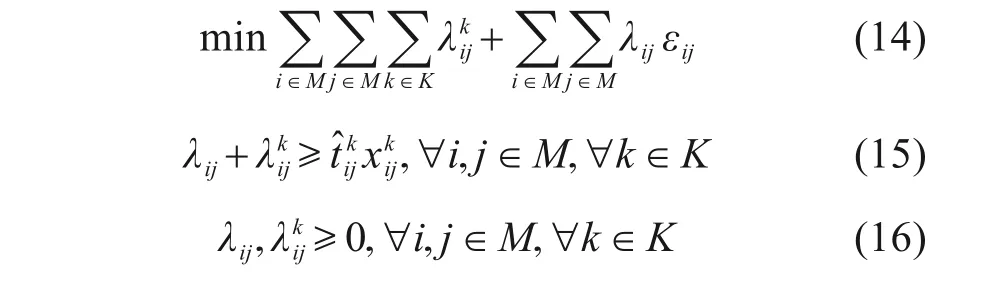
引入辅助变量c，可得到式(17)～(20)：

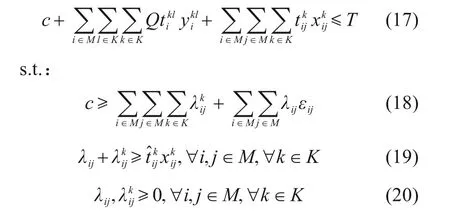
将运输过程中的碳排放根据碳税税率转化为排放成本，与运输成本共同纳入总成本中，这时模型转变为：

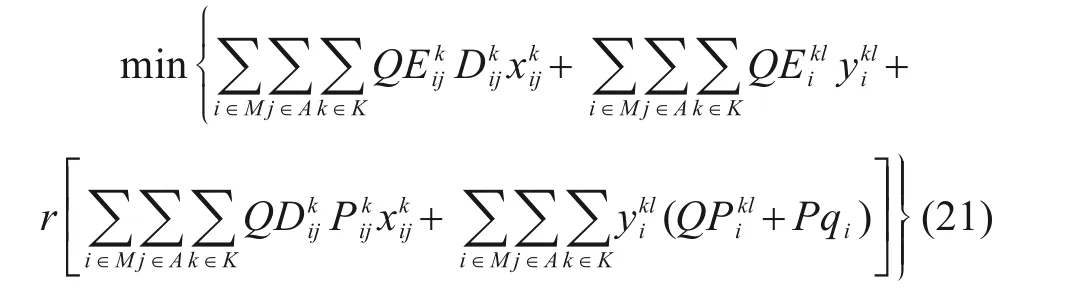
目标函数(21)表示求最低运输总成本，其中包括运输总成本及碳排放成本。同时，约束(6)～(10)，(12)和(17)～(20)成立。本文模型经转化后为易求解的混合整数线性规划模型(MⅠLP)，因此可调用求解器直接计算。基于以上分析，利用matlab2017a 中Yalmip 工具箱进行编程，并调用Gurobi9.1.2求解。

3 算例分析

3.1 背景介绍及参数说明

根据中亚班列线路规划，以往由日、韩经天津港过境运往吉尔吉斯斯坦、乌兹别克斯坦等中亚地区国家的货物，均需通过霍尔果斯、阿拉山口口岸出关。由于疫情影响，全球海运通航不畅，导致中欧、中亚班列开行量飞速增长，口岸货物堆积,班列难以及时出境。为缓解通行压力，相关部门开辟全新出境通道——伊尔克什坦口岸。综上，本文以天津港为起点，伊尔克什坦口岸为终点，在合理时间限制下，综合考虑经济效益及环境影响，寻求天津港至中亚国际运输国内段的运输新方案，验证枢纽拥堵对绿色多式联运碳排放及路径决策的影响。模型中相关参数参考2019年《交通运输行业发展统计公报》、《2019年铁道统计公报》、洛杉矶港2019年“Ⅰnventory of Air Emissions”、《2006 ⅠPCC 国家温室气体清单指南》及相关文献和网络信息确定，各节点间距离经中国铁路地图集及中国公路网查阅得到(见图1)。

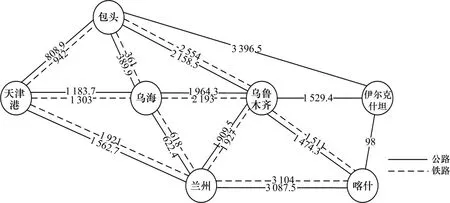
图1 天津港至伊尔克什坦口岸运输网络Fig.1 Transport netwok from Tianjin Port to Yierkstan Port

3.2 结果分析

3.2.1 鲁棒优化对路径选择的影响

取r=10，T=82，将扰动比例设 为10%，设置多个不确定参数进行实验，结果如表1所示(Δt为不确定情况与确定性情况下的运输时间差)。当不确定时间参数取0 时，模型转为确定性模型；随着参数值增加，为满足总时间限制，最优路径决策变化为时间较短但成本较高的路径，但是，不确定参数导致的运输时间变化达到一定程度才能够影响路径决策，否则，不会影响路径变化；而不确定时间参数取1时，运输时间波动最大也能保证方案可行，受限于时间要求，方案为成本更高但时间较短的运输方案。该实验验证了鲁棒优化对多式联运路径选择不确定性的随机模拟是有效的。

表1 各不确定参数下的最优路径Table 1 Optimal path under different uncertain parameters

3.2.2 枢纽拥堵对于碳排放变化的影响

取Q为100 t，T为89，在服务效率μ一定时，调整到达率λ，观察其对排放产生的影响，结果如表2 所示，其中P′2为正常转运过程产生的总排放(不含拥堵情况)。对比实验1～3，当到达率与服务效率差距较大时，即使最优路径决策未发生变化，但由于枢纽处拥堵产生的碳排放增加，进而使得运输总成本增加，只是增加的幅度较小、速度缓慢；而分析实验4～7 可得，随着到达率增加，队列长度增加，枢纽处产生的碳排放迅速增加，路径选择也随之发生变化，这时由于等待时间较长，为满足总时间限制，最优决策变化为碳排放较高但运输时间较短的运输方案；当到达率增加到一定程度，拥堵过程中产生的排放甚至会超过正常装卸等服务产生的排放。

表2 不同拥堵状况下对于排放的影响Table 2 Ⅰmpacts of different congestion conditions on emissions

3.2.3 枢纽拥堵对于绿色多式联运路径不确定性的影响

为探究转运枢纽处拥堵现象对多式联运路径决策的影响，将T设置为89，不确定时间参数εij设置为0.5，进行多组对照实验，具体结果如表3 所示(T′为运输过程中转运总时间)。对照组Ⅰ说明，当货运量为固定值，且服务效率也固定时，枢纽拥堵程度取决于到达率与服务效率的差距，到达率显著小于服务效率，平均等待时间较短，拥堵现象轻微，路径决策未发生变化；当二者较为接近时，集装箱平均等待时间增加迅速，拥堵状况较为严重，路径发生变化；当到达率大于服务效率时，即使两者差距较小，拥堵时间也会迅速增加，总时间限制下，影响路径选择。对照组Ⅱ说明，货运量的变化影响着等待时间，等待时间随货运量增加而增加。当集装箱到达率与转运服务率差距较大时，货运量的变化对于拥堵时间的影响较不显著，只有货运量增加到一定程度才会导致运输路径的变化；当集装箱到达率与转运服务率差距较小时，货运量的变化对于拥堵时间的影响较为显著，进而影响路径决策。对照组Ⅲ说明，当货运量固定，提高转运服务效率后，集装箱平均等待时间随之缩短，延迟现象减轻。到达率与服务率差距较大时，提高枢纽的服务效率很难影响多式联运的最优路径决策，这是由于此时枢纽的服务效率对于相应的到达率来说已经处于较高水平，枢纽处转运时间较短，不足以影响路径决策；到达率与服务率相差较小时，提高枢纽转运服务效率后，缩短了集装箱等待时间，路径发生变化；然而，当服务效率提高至一定水平，这时枢纽处的拥堵现象对多式联运的路径选择不产生影响。

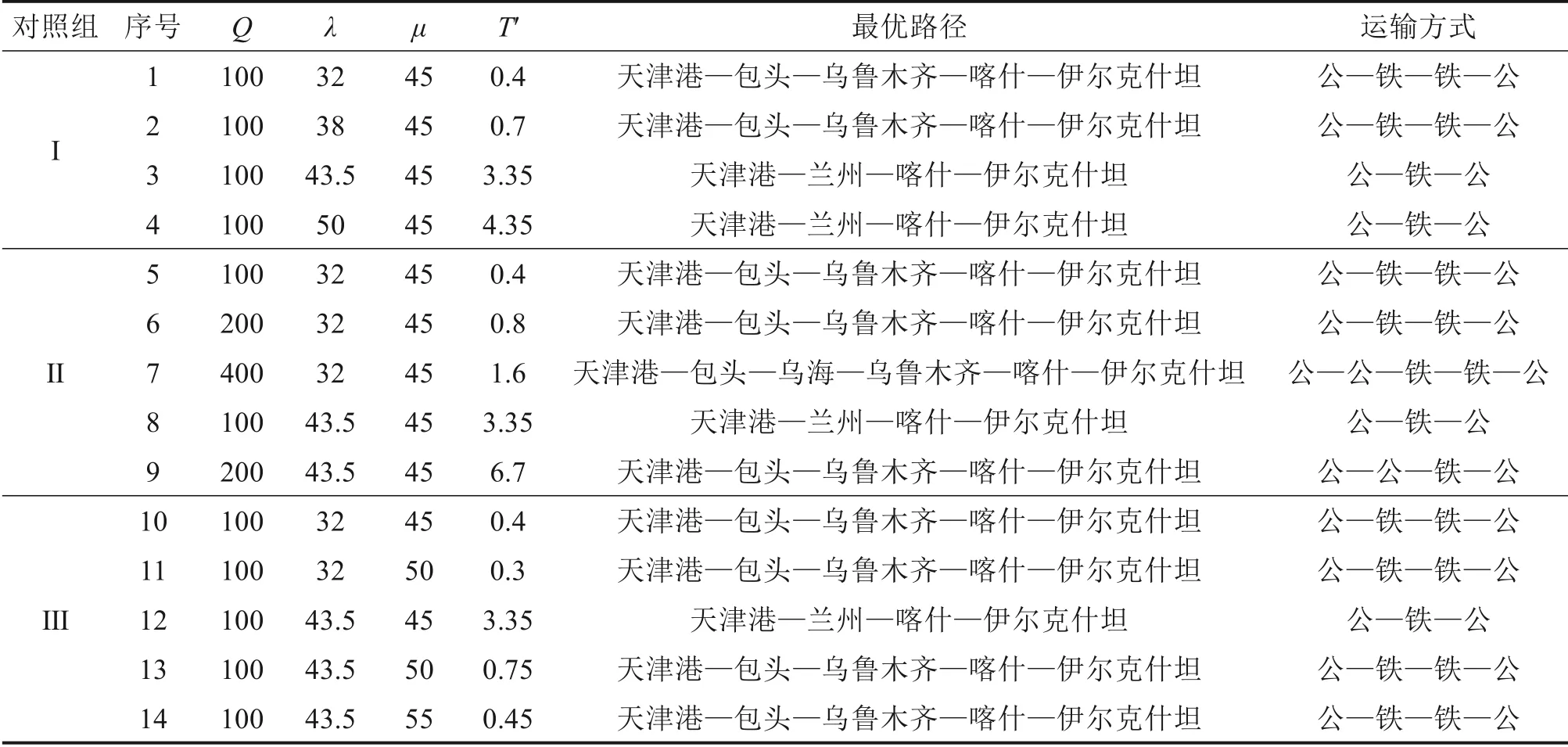
表3 不同拥堵状况下的最优路径选择Table 3 Optimal path selection under different congestion conditions

4 结论

1) 基于基数不确定集合构建的鲁棒优化模型能够准确描述多式联运过程中运输时间的波动情况，同时，决策者可以根据自身对于运输时间的敏感度调整相应参数，选择不同的运输方案。

2) 经算例分析表明：枢纽拥堵导致的延迟直接关系着运输时间，一定时限内影响最优路径决策，使得路径发生变化；而由于拥堵导致增加的碳排放，虽然不能直接影响最优路径发生改变，却使得总排放量增加，进而导致总成本增加。对于繁忙的枢纽，拥堵过程中产生的排放甚至超过了正常转运过程中的排放。在今后研究中，可以考虑利用动态优化排队系统模拟枢纽处的拥堵现象；深入探究低碳政策中相关参数设置对于枢纽拥堵情况下多式联运排放及路径决策的影响；针对单阶段鲁棒优化结果较为保守的不足，可使用两阶段鲁棒优化方法模拟运输过程的不确定性。