APOS 理论下几何画板与三角函数图象变换整合教学的实践研究

广东省广州市从化区第二中学(510900) 叶润娟

1 APOS 理论下几何画板与三角函数图象变换整合教学研究的现实背景及意义

1.1 学科知识内在联系的需要

三角函数图象变换是学习了三角函数的概念及其性质后的应用知识,根据APOS 理论中的(Scheme)阶段,此时的三角函数概念以一种综合的心理图式存在于脑海里, 在函数知识体系中占有特殊的地位, 由三角函数图象到函数y=Asin(ωx+ϕ)图象的学习,是对三角函数概念学习中与其他概念学习的区别与联系的学习阶段,对函数概念模块的教学有实际的指导意义.

1.2 高中数学新课程标准使本实践研究成为必然

《普通高中数学课程标准(2017 年版,2020 年修订)》指出,结合具体实例,了解y=Asin(ωx+ϕ)的实际意义;能借助图象理解参数ω,ϕ,A的意义,了解参数的变化对函数图象的影响. 课标对此教学内容是“掌握”“了解”的要求,同时为后续“五点”作图打好基础,此教学内容是三角函数模块中的重要内容之一.

1.3 几何画板与三角函数图象变换整合有利于培养学生直观想象的数学核心素养

几何画板直观动态展示图象的变化过程, 为学生创设数学情景, 并在熟悉的数学情景中, 借助图形的性质和变换(平移、伸缩) 发现数学规律, 解决参数ω,ϕ,A对函数y=Asin(ωx+ϕ)的图象影响,以及使学生更容易地掌握三角函数图象“先平移后伸缩(周期)”和“先伸缩(周期)后平移”得到图象问题,从而培养学生直观想象的数学核心素养.

2 发现问题

在实际教学过程中,学生直观想象能力不够强,对三角函数图象“先平移后伸缩(周期)”和“先伸缩(周期)后平移”得到图象问题感到困惑,下面以两个例子说明:

本题是选自人民教育出版社《普通高中教科书数学第一册》第239 页练习的第二题的(2)问. 按教材的学习,绝大多数学生能选出正确的选项B,但也有小部分的同学出现错误的选项,其中集中在选项A,课后经过跟学生面谈发现这部分学生是不能理解参数ω对函数y=Asin(ωx+ϕ)的图象影响,认为本节内容比较抽象,难以理解并掌握有关的结论,并对此学习内容产生畏惧的心理.

本题选自2011 年高考全国理科数学Ⅰ卷第6 题,考查三角函数的图象变换. 绝大多数学生都能选出正确的选项,但是其中大部分学生并不能理解为什么ω需要取到最小值,而不是唯一确切的值,也就是对于此类综合性较强的三角函数图象变换问题,存在不少的数学优等生也未能完全掌握理解三角函数的图象参数ω,ϕ,A的意义,作图和读图的能力较弱,不能从图象的角度分析解决图象变换问题,简单地从记忆中的结论解决问题,这是不符合课标育人的要求.

3 教学实践研究的设计、实施、总结、反思

3.1 所选内容

人民教育出版社《普通高中教科书数学第一册》第五章5.6.2 函数y=Asin(ωx+ϕ)的图象第一课时.

3.2 方法

选取高一7,8 班两个普通班,且7 班为实验班,8 班为对照班.

3.3 实施

(1)高一7 班作为实验班,使用几何画板进行教学,并使用导学案教学和小组合作学习的教学管理方式. 目的是通过几何画板创设问题的情景,直观动态地展示参数ω,ϕ,A对函数y=Asin(ωx+ϕ)的图象影响,从而达到本节课的教学目标,增强学生学习本节课的兴趣,培养学生观察图象的,分析图象,总结数学规律.

(2)高一8 班作为对照班,请按书本教学设置过程教学.

(3)通过课堂练习和课后作业,对学生答题情况进行统计.

(4)课题组成员集体研讨,在实验班教学过程中的优点与不足之处,从而得出结论.

有关教学探究片段描述如下:

探究一参数ϕ对函数y= sin(x+ϕ)的图象影响,体会平移变换

如图1,图2 所示,通过改变ϕ的大小,让学生观察图象位置关系变化,若ϕ= 2 弧度时,y= sin(x+2)的图象是函数y= sinx的图象向左平移2 个单位得到的;若ϕ=-2 弧度时,y= sin(x-2)的图象是函数y= sinx的图象向右平移2 个单位得到的. 接着动态展示y=sin(x+ϕ)的图象,改变ϕ的大小,由特殊到一般,并引导学生总结归纳出ϕ对函数y=sin(x+ϕ)的图象影响;类似地,按图3 至图6 让学生总结出另外两个参数ω,A对图象的影响,得出y= sinx图象通过平移伸缩得到函数y=Asin(ωx+ϕ)的图象. 这样通过几何画板创设问题情景,使学生对三角函数图象变换的知识形成过程有着深刻的体会,掌握三角函数平移和伸缩变换的规律.

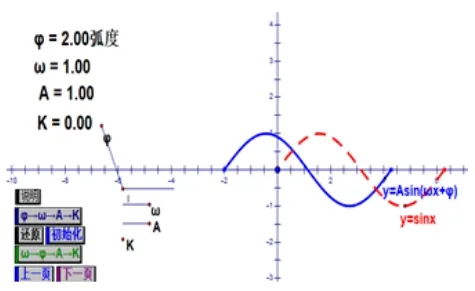
图1

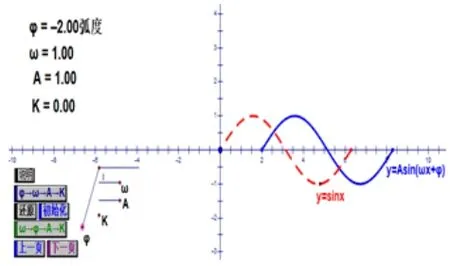
图2

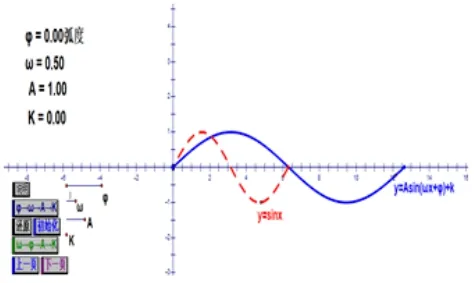
图3

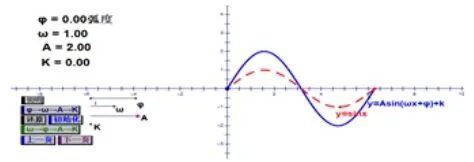
图6

探究二参数ω对函数y=sin(ωx+ϕ)的图象影响,体会伸缩(周期)变换

探究三参数A对函数y=Asin(ωx+ϕ)的图象影响,体会振幅变换

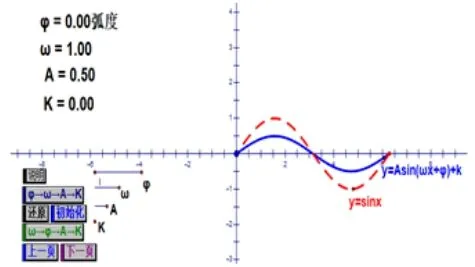
图5

探究四参数k对函数y=Asin(ωx+ϕ)+k图象的影响. 同样根据以上教学过程探究,拖动k所在线段,可以观测到其图象的动态变化图象,得到平移的“上加下减”.

探究五难点突破. 采用“试误法”,区分“先平移后伸缩(周期)”与“先伸缩(周期)后平移”图象的差别. 具体如下:

4 结束语

通过“几何画板”与课堂教学整合的课堂, 让学生直观想象中分析总结,掌握三角函数图象变换的平移、伸缩变化的规律, 能激发学生学习讨论数学问题的兴趣, 符合APOS理论两个阶段A-Action(操作活动阶段)和P-Process(过程阶段),即在活动阶段通过几何画板生成动态图象感知直观背景,在过程阶段使用几何画板作为实验平台改变约束条件使学生获得三角函数图象变换规律特征,培养学生发现问题、分析问题、解决问题的能力,让学生了解到数学也可以通过做实验验证结论,提高学生学习数学的兴趣. 故上述教学实践研究,均能达到预设目的,改善教学,培养学生逻辑推理、数学抽象、直观想象、数学运算、数据分析、数学建模的数学核心素养.