因式分解在高中数学中的应用——从2021 年全国乙卷压轴题谈起

江苏省常州市第五中学(213000) 毕文联

安徽省黄山市屯溪第一中学(245000) 吴雪萦

2021 年高考已经落下帷幕, 在对全国各类高考题研究时,今年全国乙卷文科的导数压轴题的解法引起了笔者思考.其实这道题的整体难度并不高,很多学生在平时模拟题中做过类似的题,但是在标准解答中运用的因式分解这部分的知识难倒了很多考生.

因式分解是初中数学非常重要的知识点,通过因式分解可以将复杂计算简单化,提高学生的解题效率和正确率. 事实上因式分解在各地中考中所占的比例并不大并没有引起老师和学生足够的重视,高中阶段虽然没有将因式分解单独讲授,但其在高中数学解题过程中却屡屡出现. 笔者将从全国乙卷这道压轴题出发,探索因式分解在高中数学中的应用.

1 试题及解答

题目(2021 年全国乙卷文科第21 题节选) 已知函数f(x)=x3-x2+ax+1. 求曲线y=f(x)过坐标原点的切线与曲线y=f(x)的公共点的坐标.

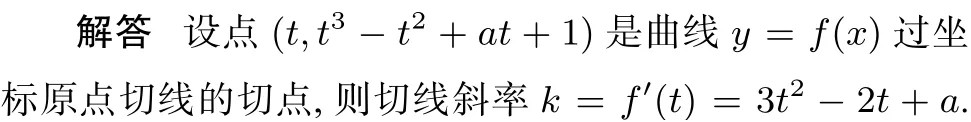
2 困难与解惑

从上述给出的标准解答中我们不难发现反复应用了因式分解去处理解题过程遇到的一元三次方程. 对于此题入手其实并不困难,绝大多数学生都有较为清晰的解题思路,但是在求出第一个一元三次方程后就束手无策了. 很多学生在看到标准答案后更是困惑,高中课本并没有教授求解一元三次方程的方法,何以想到这样因式分解呢?

事实上,在高中阶段我们所遇到的两次以上方程大多数都是以一些比较常见的数作为方程的解. 因此对于上题中的两个三次方程可以这么去求解(以方程2t3-t2-1 = 0为例) : 首先通过代入一些常见的数不难发现t= 1 满足方程, 于是原方程可以分解为(t-1)(mt2+nt+q) = 0,其中m,n,q均为常数; 然后展开通过待定系数法可以确定m=2,n=1,q=1.

3 思考与应用

因式分解主要有两个作用: 一是方便约分化简;二是可以判断多项式的正负符号. 作用一是从初中开始我们所一直在用的,作用二的应用从进入高一起一直持续到高三. 从集合到函数单调性的判断,从指数运算到基本不等式,从三角函数到数列,从解析几何中计算的简化到高中数学中最难的导数部分,因式分解都有着举足轻重的地位.

既然因式分解在高中数学中有如此基础和核心的地位,下面我们就一起领略因式分解在高中数学中的应用.

例1 (2020 年全国Ⅰ卷改编) 已知集合A={x|x2-3x-4=0},B={-1,3,4,5},求A ∩B=( ).

解由不等式x2-3x-4=0,有(x-4)(x+1)=0,进一步x1=-1,x2=4,所以A={-1,4},A ∩B={-1,4}.

集合是进入高中后首先学习的内容,也是每年高考必考的基础性知识,题目设置并不难主要涉及求解结合中的元素,而常见的主要是求解方程以及不等式,这就会不可避免的需要用到因式分解.

例2 (苏教版必修第一册习题5.3) 证明函数f(x) =-x3+1 在区间(-∞,0]上是减函数.

解设x1＜x2≤0,则

解由题意得

本题考察了三角函数公式的应用,首先利用二倍角公式和平方关系配方化简,这其中便应用了因式分解. 三角函数运算中有很多乘除法和加减法转换的题目,结合三角函数自身具有的公式就有了一套因式分解的方法,熟练应用因式分解可以降低求解三角函数题目的计算量,进而提高解题效率和正确率.

例6 (2015 年全国Ⅰ卷理科节选)Sn为数列{an}的前n项和,已知a2n+2an=4Sn+3,an ＞0,求{an}的通项公式.

解由a2n+ 2an= 4Sn+ 3, 可知a2n+1+ 2an+1=4Sn+1+3,两式相减得a2n+1-a2n+2(an+1-an)=4an+1,即2(an+1+an) =a2n+1-a2n= (an+1+an)(an+1-an).因为an ＞0,所以an+1-an=2,又a21+2a1=4a1+3,故a1=-1(舍)或a1=3,则{an}是首项为3,公差d=2 的等差数列. 因此{an}的通项公式an=3+2(n-1)=2n+1.

本题主要考察根据数列的递推公式求通项公式,题目难度并不大在高考数学中也是基础题,通过作差法即可求出答案. 教材中主要向学生讲授的等差数列与等比数列相关知识,但是学生在解题时常会遇到变形后的数列(如上题),由于看不出数列所具有的特性而束手无策. 而这些题目常常会涉及到因式分解,许多题目只有通过因式分解化简以后才能看出等差数列或者等比数列,熟练掌握因式分解将会助力学生解决此类问题.

例7 (2021 江苏南京高三二模节选) 在平面直角坐标系xoy内,已知抛物线y=x2的焦点为F,P为平面直角坐

本题的难度较高,解题的关键在于能否运用因式分解的方法进行计算. 大多数同学都具有由垂直关系列出等式的意识,但在求解方程时就障碍重重,甚至自我怀疑是不是解题角度出错了. 在每年各地的高考中解析几何是必考内容之一,也是高中最难的知识点之一,其中的计算量更是让很多同学折戟沉沙. 在解析几何复杂且大量的计算中,因式分解是基本解题技巧,合理的使用因式分解往往可以“拨开迷雾乾坤有,又见花香鸟语传”.

本题考查了导数和函数单调性的关系以及分类讨论的思想,考查了运算能力和化归能力. 笔者通过调查发现,学生存在的主要问题是没有因式分解的思维,进而无法进行分类讨论.导数对于研究函数的作用是毋庸置疑的,在求导后如何判断导函数的正负符号是关键,因式分解恰恰判断正负符号的一把“钥匙”.

思考: 高中数学中大部分知识都由初中基础发展而来,在内容上更多、更深、更广、更抽象[1]. 通过上述应用我们不难发现因式分解是串起整个高中数学的重要线索,但是在高中数学课本中却没有哪一个章节专门介绍因式分解的做法.笔者认为这就是一种能力的缺失,同时也是初中和高中知识点的一个脱节,这恰恰可能是许多学生进入高中后跟不上的原因之一. 我们作为教育工作者要在时常的教学过程中注意初高中知识点的衔接, 不能仅仅将知识讲授停留在教材上,更应当立足教材着眼于解决学生各个阶段知识体系衔接的问题.

总之,因式分解是高中数学中知识体系中重要的一部分,做好初、高中知识衔接教学是高中教学的重要环节,其最终目的是让学生形成自己的有效知识网络[2]. 学生只有形成有效的知识网络,才能在学习和解题上事半功倍.