四面体六面共点的一个充要条件*

赣南师范大学数学与计算机科学学院(341000) 曾建国

1 引言

为了探求四面体中共点面问题的证明方法,人们作了大量的探索研究,也涌现出一大批研究成果. 例如,人们将三角形塞瓦(Ceva)定理及逆定理[1]类比推广至四面体中,已得到下面的结论(参见图1)

上述结论为证明四面体中有关6 面共点问题提供了重要的方法和依据. 但有些美中不足的是: 命题2 给出的四面体中6 面共点的充分条件显得比较繁琐,且命题2 与命题1并非互逆命题(从而并未得到6 面共点的充分必要条件);另外,在实际应用中,应用命题2 证明四面体中6 面共点问题时无法一步到位,往往需要进行繁琐的分类讨论,不够便捷.笔者在以往的研究[5]中对此体会颇深.

本文尝试探求四面体中有关6 面共点的新的充要条件,并举例说明其应用.

2 四面体六面共点的一个充要条件

为便于叙述,本文约定: 四面体A1A2A3A4中,顶点Ak所对侧面记为Δk(1 ≤k≤4).

苏化明在其论著“四面体”中证明了下面的结论(参见图1).

命题3[6]设Bij是四面体A1A2A3A4的棱AiAj上一点(1 ≤i ＜j≤4), 如果每个侧面Δk上的三条塞瓦线(侧面三角形Δk的顶点与对边上点Bij的连线, 下同) 都分别交于一点Mk(1 ≤k≤4)(例如侧面Δ1内有A2B34、A3B24、A4B23交于一点M1, 等等) , 那么A1M1、A2M2、A3M3、A4M4必交于一点M.

命题3 的结论可以拓广.

一方面,题设中Bij是四面体A1A2A3A4的“棱AiAj上一点”可以放宽为“棱AiAj所在直线上一点”;另一方面,由结论“A1M1、A2M2、A3M3、A4M4交于一点M”可得“6 个平面A1A2B34、A1A3B24、A1A4B23、A2A3B14、A2A4B13、A3A4B12交于一点M”. 而且,反过来结论也成立. 即有关于四面体中6 面共点的一个充要条件如下：

定理1 设Bij是四面体A1A2A3A4的棱AiAj所在直线上一点(1 ≤i ＜j≤4),则6 个平面A1A2B34、A1A3B24、A1A4B23、A2A3B14、A2A4B13、A3A4B12交于一点M(M非四面体顶点,且直线AkM与侧面Δk(1 ≤k≤4)不平行)的充要条件是: 每个侧面Δk上的三条塞瓦线分别交于一点Mk(1 ≤k≤4)且A1M1、A2M2、A3M3、A4M4互不平行.

证明(1)必要性.

设6 个平面A1A2B34、A1A3B24、A1A4B23、A2A3B14、A2A4B13、A3A4B12交 于 一点M. 依题设, 直线AkM与侧面Δk不平行,则它们相交于一点Mk(1 ≤k≤4). 如图1, 因A1M与侧面Δ1交于点M1, 显然M1就是A2B34、A3B24、A4B23的交点. 同理可证其他各侧面Δk上的三条塞瓦线也分别交于一点Mk(2 ≤k≤4). 因A1M1、A2M2、A3M3、A4M4交于一点M,故它们互不平行.

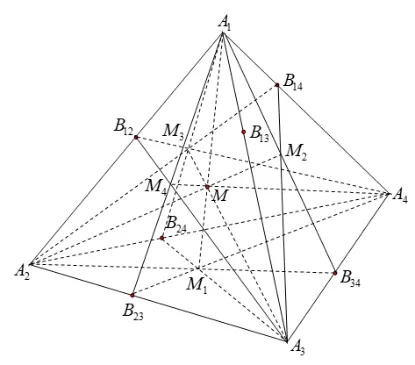
图1

(2)充分性.

设各侧面Δk上的三条塞瓦线分别交于一点Mk(1 ≤k≤4) 且A1M1、A2M2、A3M3、A4M4互不平行. 在侧面Δ1内, 由A2B34、A3B24、A4B23交于一点M1知, 平面A1A2B12、A1A3B24、A1A4B23相交于直线A1M1.

同理可得:

平面A1A2B12、A2A3B14、A2A4B13相交于直线A2M2;

平面A1A3B24、A2A3B14、A3A4B12相交于直线A3M3;

平面A1A4B23、A2A4B13、A3A4B12相交于直线A4M4.

依题设可证明,直线A1M1与平面A2A3B14必相交于一点M.

事实上, 若A1M1//平面A2A3B14(图2), 注意到平面A1A3B24经过A1M1, 且与平面A2A3B14相交于A3M3,则有A1M1//A3M3, 与题设矛盾! 故直线A1M1与平面A2A3B14必相交于一点M.

图2

因此, 在图1 中, 由M ∈A1M1⊂平面A1A2B34、及M ∈平面A2A3B14可得M ∈A2M2.

同理可证M ∈A3M3,M ∈A4M4.

这就表明点M是6 个平面A1A2B34、A1A3B24、A1A4B23、A2A3B14、A2A4B13、A3A4B12的公共点. 定理1 获证.

关于定理1 的几点说明:

(1)关于“非四面体顶点”的限定.

当6 个平面A1A2B34、A1A3B24、A1A4B23、A2A3B14、A2A4B13、A3A4B12交于一点M恰为四面体顶点A1时,则在侧面Δ1内,A2B34、A3B24、A4B23不一定共点(如图3),此时定理1 的必要性不成立. 因此定理1 中必须限定“M非四面体顶点”.

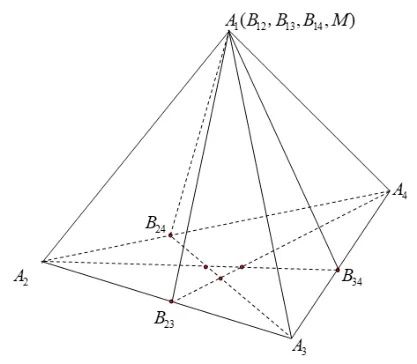
图3

(2)关于“直线AkM与侧面Δk不平行”的限定.

当M在平行于某侧面Δk的直线AkM上时, 如图4,若A1M//侧面Δ1,不难证明Δ1中三条塞瓦线互相平行(A3B24//A2B34//A4B23).因此,将定理1 的必要性改述为“若6 个平面A1A2B34、A1A3B24、A1A4B23、A2A3B14、A2A4B13、A3A4B12交于一点M(M非四面体顶点), 则每个侧面上的三条塞瓦线都分别交于一点或平行”仍为真命题.因此类特殊情形下充分性的讨论比较复杂(受篇幅所限),所以在定理1 中考察6 面共点的充要条件时,索性排除了“直线AkM与侧面Δk平行”的特殊情形,这对定理1 的应用范围影响并不大.

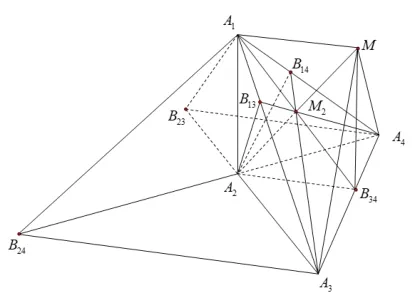
图4

3 应用举例

在研究四面体中有关6 面共点问题时,应用本文定理1完全有可能改进以往的方法,使证明过程变得简洁明快. 下面举例说明.

例1 (四面体重心定理)[7]经过四面体的一条棱及其对棱中点的平面称为四面体的中面,证明: 四面体的6 个中面交于一点(重心).

证明设四面体A1A2A3A4的棱AiAj的中点为Bij(1 ≤k≤4), 则各侧面Δk的三条塞瓦线就是侧面三角形Δk的三条中线, 必交于其重心Mk(1 ≤k≤4), 且A1M1、A2M2、A3M3、A4M4互不平行. 根据定理1 的充分性知, 6 个中面A1A2B34、A1A3B24、A1A4B23、A2A3B14、A2A4B13、A3A4B12交于一点M(重心). 证毕.

笔者曾将三角形葛尔刚(Gergonne)点(连接三角形的顶点及对边与内切圆切点的直线,三线共点)[8]的性质推广至有内棱切球(以下简称棱切球,充要条件是四面体的三组对棱之和相等)[9]的四面体中,即

例2 (四面体的葛尔刚(Gergonne)点)[5]若四面体有棱切球,则过每一条侧棱与棱切球的切点及其对棱作平面,6 个平面交于一点.

应用定理1 就有下面的简洁证法(参照图1)

证明设四面体A1A2A3A4的棱切球与侧棱AiAj切于点Bij(1 ≤i ＜j≤4), 须证明6 个平面A1A2B34、A1A3B24、A1A4B23、A2A3B14、A2A4B13、A3A4B12交于一点M. 在侧面Δ1中,易知[5],棱切球面被侧面Δ1截得的截面圆就是Δ1(即ΔA2A3A4)的内切圆,则B34、B23、B24是ΔA2A3A4的内切圆分别与边A3A4、A2A4、A2A3的切点.故A2B34、A3B24、A4B23交于一点M1(ΔA2A3A4的葛尔刚(Gergonne)点).

同理可以证明: 其余各侧面Δk上的三条塞瓦线也分别交于Δk的葛尔刚点Mk(2 ≤k≤4). 显然A1M1、A2M2、A3M3、A4M4互不平行.

根据定理1 的充分性知,6 个平面A1A2B34、A1A3B24、A1A4B23、A2A3B14、A2A4B13、A3A4B12交于一点M. 证毕.

4 结束语

本文定理1 的意义在于,应用定理1 证明四面体中某些6 面共点问题时,可以避开应用四面体Ceva 定理(命题2)这一步骤,转而证明各侧面三角形中的三线共点问题(只需应用三角形Ceva 定理),是一种有趣的“降维处理”方法,因而在实际应用中可以避免分类讨论,从而达到化繁为简的效果.如上面的例2 就大大简化了笔者之前的证法[5]. 可以预见,本文所得关于四面体6 面共点的充要条件应该具有广阔的应用前景.