具有不同侧链长度的聚对苯乙炔类衍生物的杨氏模量

吴鲁超,田益明,闫伟青,钟高余

(复旦大学 材料科学系,上海 200433)

共轭聚合物材料由于具有较好的延展性、可伸缩性和灵敏度,被广泛地应用于柔性发光器件、太阳能电池、有机薄膜晶体管和压阻传感器等电子器件[1-5]。目前,对共轭聚合物的电学特性研究比较深入[6-11],但对其力学特性的研究还比较欠缺[6-7],确定聚合物材料的杨氏模量等力学性能最常用的方法是通过计算纳米压痕技术所测得的小压力下卸载曲线最高点的斜率,但对不同厚度的薄膜施加压力,压力卸载时最高点的斜率明显会有所不同,从而导致通过该方法测量得到的杨氏模量结果会存在较为明显的差异[12-13]。例如,O'Connor等[12]测量poly(3-hexylthiophene)(P3HT)的杨氏模量为0.25 GPa,而Tummala等[13]测量的结果为1.6 GPa,二者测量的结果相差大于5倍。此外,侧链的长度、密度、位置和分布对聚合物材料的力学性能也有较大的影响,研究人员已经发现侧链长度对聚合物的拉伸模量和力学弹性起着关键的作用[14-16]。因此,开发出一种先进的确定杨氏模量的方法,理解共轭聚合物分子结构和机械性能的关系对设计高性能的柔性电子器件至关重要。然而,由于侧链分布和层次结构的复杂性,建立这种关系仍然具有挑战性。

由于共轭聚合物的侧链长度会影响材料的结晶度、链的排列和玻璃化转变温度等,从而导致对材料的力学性能进行理论预测变得十分困难[17-18]。另外,为了提高共轭聚合物的导电性能,通常选择掺杂部分高性能的导电晶体,这进一步复杂化侧链的效应[19-21]。当共轭聚合物受到小压力时,较硬的共轭主链很难被压缩,主要由较为柔软的非共轭侧链提供弹性,侧链的长度对刚度,杨氏模量等机械性能有着显著的影响。所以通过对侧链进行直接测量来研究侧链长度和机械性能之间的关系对优化和定制柔性电子器件及敏感材料具有明显的优势。

在本文中,我们用纳米压痕仪测试了4种聚对苯乙炔(Poly-Phenylene Vinylene,PPV)类衍生物薄膜外加压力随压入深度的变化曲线,并使用伦纳德 琼斯势方程解释并拟合了卸载曲线,从而得到杨氏模量随应力的变化关系。此外,我们通过引入一个重复单元内侧链上的分子量与该重复单元的总分子量的百分比,从实验数据总结出PPV类衍生物杨氏模量的经验公式。通过该经验公式,可以根据分子量占比,估算得到不同PPV类衍生物在任意较小压力下的杨氏模量,为初步了解材料的分子结构和机械性能的关系提供一种简要的分析方法。

1 实 验

1.1 样品

本文研究的4种PPV类共轭聚合物是从商业公司(Sigma-Aldrich)购买,这4种PPV类材料分别为:聚[2-甲氧基-5-(2-乙基己氧基)-1,4-苯乙炔](poly-2-methoxy-5-(2-ethylhexyloxy-1,4-phenylenevinylene,MEH-PPV)、聚[2-甲氧基-5-(3′,7′-二甲基辛氧基)-1,4-苯乙炔](poly[2-methoxy-5-(3′,7′-dimethyloctylocxy)-1,4-phenylenevinylene],MDMO-PPV)、聚[2,5-双(3′,7′-二甲基辛氧基)-1,4-亚苯基亚乙烯](poly[2,5-bis(3′,7′-dimethyloctyloxy)-1,4-phenylenevinylene],BDMO-PPV)和聚[2,5-二(3,7-二甲氧基)氰基对苯二亚甲基](poly(2,5-di(3,7-dimethyloctyloxy)cyanoterephthalylidene),CNPPV),分子结构式如图1(a)所示。我们首先使用丙酮、乙醇、去离子水依次对硅片进行5 min超声清洗,再放入干燥箱进行烘干,然后用强力胶将清洁烘干后的硅片粘在厚玻璃上来作薄膜基底。再用氯苯做溶剂,将上述4种聚合物配制成浓度为20 mg/m L的溶液,为了让溶质充分溶解在溶剂中,在配置溶液时需将溶液加热到70℃并用磁力棒搅拌48 h。最后将约150μL溶液均匀滴涂在20 mm×25 mm的硅片上,待溶剂在室温下自然挥发后即可形成结构简单的样品。

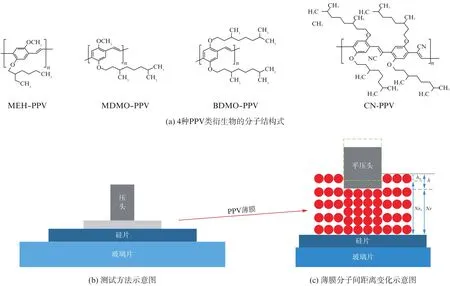
图1 4种PPV类衍生物的分子结构式和机械性能测试原理图Fig.1 Mokcular structurd formula and mechanical property analysis diagram of four PPV derivatives

1.2 测试

在测试方面,我们预先使用台阶仪(BRUKER DEKTAK 150)分别测量了所制备的4种PPV类共轭聚合物薄膜样品的厚度,结果如下:MEH-PPV,8.73μm;MDMO-PPV,15.5μm;BDMO-PPV,14.0μm;CNPPV,7.35μm。然后通过纳米压痕仪(CSM instruments Ultra Nanoindentation)测试得到外力随压入深度的变化曲线。由于柔性电子器件是在外加压力较小情况下具有较强的力学敏感性,即需要具有较强的力学感知,同时为了只考虑侧链对材料机械性能的影响,我们控制材料形变小于5%,所施加的最大压力为0.1 m N,而平面受力更符合实际触觉感知的情况,所以主要使用平压头进行纳米压痕测试。图1(b)为测试方法示意图,图1(c)为薄膜受到压力后,分子间距离变化示意图。纳米压痕仪的压头为直径20μm的金刚石平底圆柱形压头。压头以0.10 m N/min的加载速率加载到0.10 m N,保持该最大加载力20 s,再以0.10 m N/min的速率进行卸载,从而获得材料在小压力下的纳米压痕曲线。

2 方 法

图2 模型中V、F、E随R的变化示意图Fig.2 The diagram of the V-R,F-R,E-R curves

通常情况下,我们用目前的测试方法,在测试材料的杨氏模量E时,是通过计算卸载曲线最高点处的斜率所对应的刚度,来反映所测材料的杨氏模量。本文是通过求解E0来推算不同压力下的杨氏模量,E0为外力卸载后,材料受力为零时的杨氏模量,它更能代表材料初始状态的力学性能。一般宏观杨氏模量是一个固定值,仅与材料本身的物理性质有关,而本文中推算的杨氏模量E是一个变量,在不同压力下不同,这说明只取决于材料本身物理性质的杨氏模量对于特殊结构的材料,比如共轭聚合物,拥有刚性的主链和柔软侧链,使用目前的表征方法计算得到的其杨氏模量并不是固定值,而是会随着压力的变化而改变。

从图1(c)中薄膜分子间距离变化的示意图可知,压入深度为h,卸载后受力为0时(即分子处于平衡状态下)的压入深度为hm。我们假设有N个分子层参与形变,且衬底没有参与形变,受压后分子间总的距离即为Nr,其中r为单位分子的平均厚度。材料受压回弹到平衡状态时,这个分子层在平衡状态下的总厚度则为Nr0,可假设为rm,则实际分子间距Nr=rm-(h-hm)。因此,分子偏离平衡位置的相对距离为

3 结果与讨论

为了更接近触觉所感知的压力范围,且主要研究侧链所发生的形变,纳米压痕仪所施加的压力不宜过大,设置最大载荷为0.1 m N,并在此最大载荷下保持20 s,观察材料加载与卸载过程中外力随压入深度的变化。图3(a)为我们测试得到的4种PPV类衍生物的外力随压入深度的变化曲线,由图可知,4种PPV类材料(MEH-PPV,MDMO-PPV,BDMO-PPV,CN-PPV)在卸载后回弹到平衡状态时(受力F为0)的速率(斜率)依次递减,这和材料侧链长度增加的顺序一致,说明这些材料的主链虽然相同,都为PPV,但侧链越长,回弹到平衡位置所需的时间越长。在测试过程中保持最大载荷20 s,材料依然发生形变,这说明在此压力下材料产生了蠕变,而蠕变受压入深度和薄膜厚度的影响,这里因为材料厚度不一致,所以蠕变的程度趋势具有一定的变化。

由于这4种PPV类衍生物薄膜在加载阶段薄膜内大部分空隙已被消除,薄膜变得更为紧密,因此通过拟合卸载曲线更能反映薄膜的弹性形变。在实验中施加小压力时,薄膜的弹性形变基本是由侧链引起,所以本文所测得的杨氏模量应该是柔软侧链的杨氏模量。我们使用以上方法拟合纳米压痕仪获得的外力随压入深度的卸载曲线,拟合结果如图3(b)所示,由图可以明显看出,拟合曲线和所测得曲线重合度较好,说明通过该拟合曲线所求得的杨氏模量基本符合被测材料的机械性能,所拟合出的3个参数可以体现出材料本身的力学性能,再通过这3个参数使用式(14)和式(15)即可求出平衡状态下的杨氏模量E0和在不同压力下侧链的杨氏模量E。

图3 4种PPV衍生物的机械性能及拟合结果图Fig.3 Schematic of mechanical properties of four PPV derivatives and the fitting curves

图3(c)为我们对卸载曲线进行拟合所求出的这4种PPV类材料的杨氏模量与外力的变化曲线图,由此图可知,杨氏模量随外加压力增加在不断变化且基本是线性的,这并不能说明我们所推算的杨氏模量不能代表材料的物理性质,只是对于共轭聚合物等有机材料通过纳米压痕仪测试得到的杨氏模量并不是一个固定值,而是可能会随着压力的增加而改变。这4种材料在压力为0.1 mN(318 kPa)下开始卸载时,其杨氏模量的大小依次为:MEH-PPV,301 MPa;MDMO-PPV,265 MPa;BDMO-PPV,178 MPa;CN-PPV,153 MPa;这与测试时仪器显示的杨氏模量MEH-PPV,286 MPa;MDMO-PPV,244 MPa;BDMO-PPV,172 MPa;CN-PPV,132 MPa基本一致,如果考虑材料的泊松比(一般不为0),则杨氏模量的计算值和仪器显示值更一致,这也验证了我们拟合方法的合理性和准确性。另外,4种PPV类衍生物的从分子结构式(见图1(a))可以看出,聚合材料侧链长度由短到长,或侧链分布由疏松变密集,而杨氏模量与侧链的疏松程度关系正好相反,即侧链越疏松,侧链长度越短,杨氏模量越大,这说明主链相同的材料,不同的侧链长度会导致杨氏模量不同,PPV类材料的杨氏模量会随侧链长度增加而降低。由图3(c)中可以明显看出侧链都是烷链的PPV材料,在回弹到平衡位置时的杨氏模量基本相同,都为烷链的杨氏模量,侧链越短,杨氏模量随外力增加的速率越快。图3(c)左上的数字为直线的斜率,表明了杨氏模量随外力增加的速率。本文所研究的材料为PPV类衍生物,它们具有相同的主链(PPV)和长短不一且分布密集程度不同的侧链(烷链)。为了更好地比较侧链含量对材料在小压力下的杨氏模量的影响,我们定义了一个参数(Sw)来表示侧链的含量,即高分子材料在一个重复单元内侧链上的总分子量占该重复单元的总分子量的百分比。由于构成侧链的原子基本相同,大多是碳和氢原子,从而可以用具体数值来表示侧链大致的长短和数目。这4种聚合物的侧链含量Sw以及杨氏模量随应力变化的斜率k如表1所示。

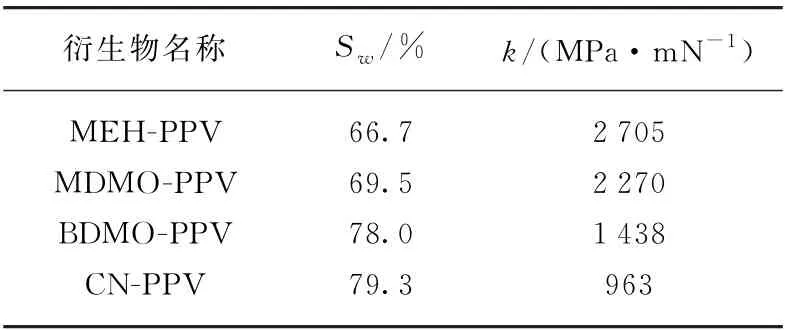
表1 4种PPV类衍生物的Sw以及杨氏模量随应力变化的斜率kTab.1 The S w of 4 PPV derivatives and the slope k of Young's modulus to stress

对这4种PPV类衍生物侧链含量的参数Sw与斜率k进行了线性拟合,可得到

该式的拟合曲线与这4种的生物的实际结果对比情况如图4所示,图中公式曲线和表1所示数据(⊗)基本吻合,这说明该线性公式能基本描述侧链含量Sw与杨氏模量随应力变化速度k的关系。通过公式(16),可以由PPV类衍生物的分子结构推算出所对应的杨氏模量随应力变化速度k的大小,从而为研究侧链长度对材料机械性能的影响提供了基础。

由图3(c)可知,这4种PPV类衍生物在压力0.1 m N以下的杨氏模量随应力变化基本为线性的,且在平衡状态下的杨氏模量E0基本一致,位于50～70 MPa之间,因此具有不同长度的烷链作为侧链的PPV类材料,其杨氏模量与外加压力大小有关,在外加压力较小,如小于0.1 m N(318 k Pa)时,其杨氏模量的经验公式为

其中:E0约为50～70 MPa,为材料在平衡状态下的杨氏模量,即烷链在外加压力为零时在卸载曲线末端的杨氏模量;F为外加压力,E为外加压力F和侧链烷链分子量占总分子量的百分比Sw的函数。公式(17)是在外加压力比较小的情况下得到的经验公式,对于外加压力如果比较大情况,如压力接近1 MPa的时,主链可能开始参与形变,材料的刚度会对杨氏模量测试结果产生影响,因此需要引入其它规律,如复合材料的杨氏模量规律,这将是我们下一步需要研究的课题。

4 结 论

总之,我们用纳米压痕仪测试了4种PPV类衍生物薄膜的外加压力随压入深度的变化曲线,使用伦纳德 琼斯势解释和拟合了卸载曲线,得到不同卸载压力下的杨氏模量,并发现4种材料的杨氏模量在平衡状态下,即受力为0时的杨氏模量E0基本一致,为(60±10)MPa。当载荷在0.1 m N(318 k Pa)卸载时,材料其杨氏模量从大到小依次为:MEH-PPV、301 MPa;MDMO-PPV、265 MPa;BDMO-PPV、178 MPa;CN-PPV、153 MPa;与纳米压痕仪所测试得到的基本一致,这说明在主链都是比较刚性的PPV的共轭聚合物中,侧链的杨氏模量随侧链长度的增加而减小。同时,侧链越长,材料恢复到初始状态(无压力)时的速度越小,所需时间越长,并且杨氏模量随外力变化的速度也更慢。另外,本文通过引入分子结构重复单元内侧链分子量与该重复单元的总分子量的百分比(Sw),推导出PPV类衍生物杨氏模量的经验公式(17)。通过该式,再根据材料的分子结构式,可计算出PPV类材料在小压力下的杨氏模量,为探索材料的分子结构和机械性能的关系提供一种简要的分析方法。