几种混合型共轭梯度法的数值性能
2022-05-30黄元元杨颖珂
黄元元, 杨颖珂
(河南科技大学 数学与统计学院, 河南 洛阳 471023)
共轭梯度法是求解无约束优化问题
minf(x),x∈n,
(1)
的有效方法之一, 最早由Hestenes等[1]提出用于求解线性方程组, 之后被Fletcher等[2]推广到求解非线性无约束优化问题(1)上. 求解非线性无约束优化问题(1)的经典共轭梯度法, 除HS共轭梯度法和FR共轭梯度法外, 还有PRP共轭梯度法[3-4]、 CD共轭梯度法[5]、 LS共轭梯度法[6]、 DY共轭梯度法[7]和DL共轭梯度法[8]等. 以这些经典的共轭梯度法为基础, 目前已提出了多种混合型共轭梯度法, 如具有充分下降性质的共轭梯度法、 混合型共轭梯度法、 三项共轭梯度法和预条件共轭梯度法等.
在多种共轭梯度法中, 具有充分下降性质的混合型共轭梯度法通常具有较好的数值性能, 因此备受关注. Hager等[9]基于HS算法提出的CG_DESCENT算法因数值性能较好而被广泛应用. Cheng等[10]利用Gram-Schmidt正交化策略, 设计了一种满足充分下降性质的共轭梯度法, 也具有较好的数值性能. 继Andrei[11-13]提出了基于经典共轭梯度算法凸组合, 设计混合型共轭梯度法的概念后, Babaie-Kafaki等[14]提出了一种基于DY和HS算法某种凸组合形式的混合型共轭梯度算法, 指出该类混合型共轭梯度算法的数值性能极大程度上依赖于组合参数的选取, 并给出了一个自适应的组合参数. 为提高该类算法的数值效果, Livieris等[15]通过极小化共轭梯度方向和有限记忆BFGS方向之间的距离, 借助拟牛顿思想, 设计了一种基于DY和HS+的改进的HCG+共轭梯度法, 该方法满足充分下降条件且在Wolfe线搜索下全局收敛.
本文在上述已有工作的基础上, 设计一类收敛的混合型共轭梯度法, 并借助CUTEst测试环境, 对该类混合型共轭梯度法的有效性进行验证, 同时与文献[15]提出的改进算法进行数值性能比较, 分析这些算法在弱Wolfe线搜索下的数值行为.
1 算法描述
经典共轭梯度法的算法框架如下: 对任意给定的初始点x0∈n, 迭代序列{xk}由
xk+1=xk+αkdk
(2)
产生, 步长αk可由弱Wolfe一维线搜索:
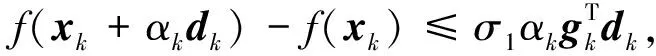
(3)
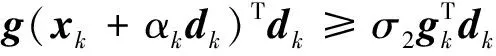
(4)
得到, 其中: 0<σ1<σ2<1;dk为搜索方向, 且
dk+1=-gk+1+βkdk,d0=-g0,
这里gk+1=f(xk+1),βk为迭代参数, 不同参数βk对应不同的共轭梯度法.经典的共轭梯度法有FR[2],DY[7],PRP[3-4]和HS[10]等, 所对应的参数βk分别定义为
FR和DY共轭梯度法通常具有较好的全局收敛性质, 但数值结果不理想; PRP和HS共轭梯度法数值结果比前两种更优越, 但理论上不能完全保证收敛性.
共轭梯度法的充分下降条件为
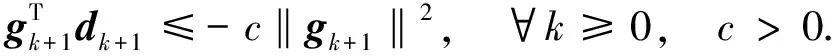
(5)
Hager等[9]提出的CG_DESCENT算法满足该充分下降条件(5), 且c=7/8, 其参数βk是基于HS算法给出的, 公式为
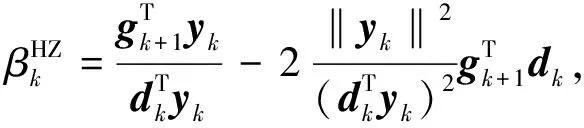
(6)
其中yk=gk+1-gk.Cheng等[10]提出的正交化共轭梯度算法, 其搜索方向dk由
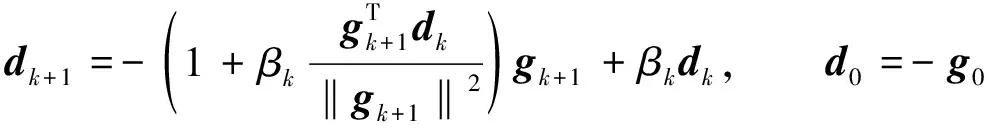
(7)
产生, 这类搜索方向满足充分下降性质(5), 且c=1.式(7)中不同的参数βk对应不同的正交化共轭梯度法.
本文在保证算法全局收敛的前提下, 设计正交化的混合型共轭梯度算法, 算法描述如下.
算法1正交化的混合型共轭梯度算法.
步骤1) 选取初始点x0∈n, 0<σ1<σ2<1,ε>0, 令k=0;
步骤2) 若‖gk‖≤ε, 则停止; 否则, 利用弱Wolfe线搜索式(3)和式(4)确定步长αk;
步骤3) 由式(2)计算新的迭代点xk+1;
步骤4) 由式(7)计算新的下降方向dk+1, 令k∶=k+1, 并转步骤2).
算法1中的参数βk不再采用经典共轭梯度法中βk的定义, 本文以经典算法中的参数βk为基础, 设计4种混合型的迭代参数, 对应的4个正交化共轭梯度法的收敛性分析证明类似于文献[10]中的理论证明, 故本文略.下面给出基于算法1框架的4个正交化共轭梯度法.
1) 基于ZL方法的共轭梯度法(HCG_ZL).
Zhang和Li[16]给出了CG_DESCENT方法的一般形式, 即定义参数βk为
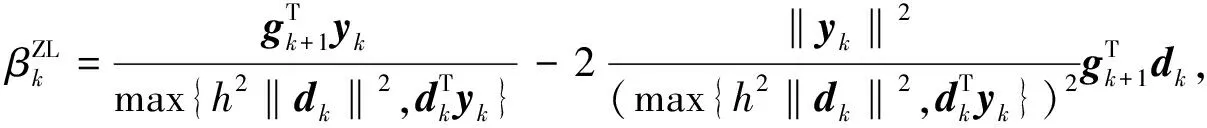
(8)
其特点是分母有正的下界.若式(7)中的参数βk采用式(8)进行迭代计算, 则算法1称为基于ZL方法的共轭梯度法, 简记为HCG_ZL算法.
2) 基于PRP和HS的混合型共轭梯度法(HCG_PRPHS).
为体现经典的PRP和HS算法的数值优势, 本文给出基于PRP和HS算法特点的参数βk, 定义为
其中ζ>0.若式(7)中的参数βk采用式(9)进行迭代计算, 则算法1称为基于PRP和HS的混合型共轭梯度法, 简记为HCG_PRPHS算法.
3) 基于DY和FR的混合型共轭梯度法(HCG_DYFR).
作为对比组, 基于DY和FR的算法定义参数βk为
此时的算法1称为基于DY和FR的混合型共轭梯度法, 简记为HCG_DYFR算法.
4) 基于DY和HS的混合型共轭梯度法(HCG_DYHS).
Babaie-Kafaki等[14]基于凸组合概念, 提出了HCG+混合型共轭梯度法, 其参数βk定义为
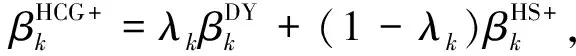
(10)
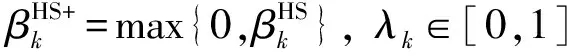
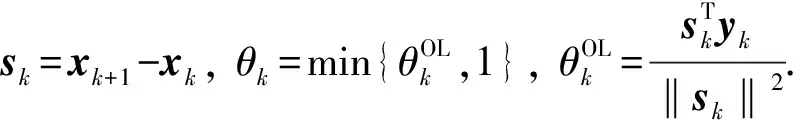
此时的算法1为自适应下降混合型共轭梯度法, 即文献[15]中的算法, 简记为ADHCG+算法.
借鉴HCG_PRPHS算法和ADHCG+算法的思想, 以凸组合的形式设计基于DY和HS的混合型共轭梯度法, 简记为HCG_DYHS算法, 为保证算法的充分下降条件, 定义参数βk为
其中vk=λkgk+1+(1-λk)yk,λk的选取与ADHCG+算法中λk的选取方式一致.
2 数值实验
下面从数值计算的角度研究HCG_ZL算法、 HCG_PRPHS算法、 HCG_DYFR算法和HCG_DYHS算法在弱Wolfe线搜索下的数值性能并与ADHCG+算法进行比较. 所有算法均在操作系统为Linux Ubuntu 12.04, 处理器为Intel(R) Xeon(R) i5-500U 2.40 GHz, 内存为8.00 GB的笔记本电脑上运行.
为使实验结果更客观, 从CUTEst测试环境中提取138个无约束优化问题对本文算法的数值性能进行比较. 在算法执行过程中, 选取终止准则为
‖gk‖∞≤max{ε,ε(1+fk)},
其中ε=10-6且fk=f(xk).弱Wolfe线搜索(3)-(4)中的参数σ1=0.1,σ2=0.9, 初始步长α0的选取准则参见文献[9].不同算法的数值结果列于表1.
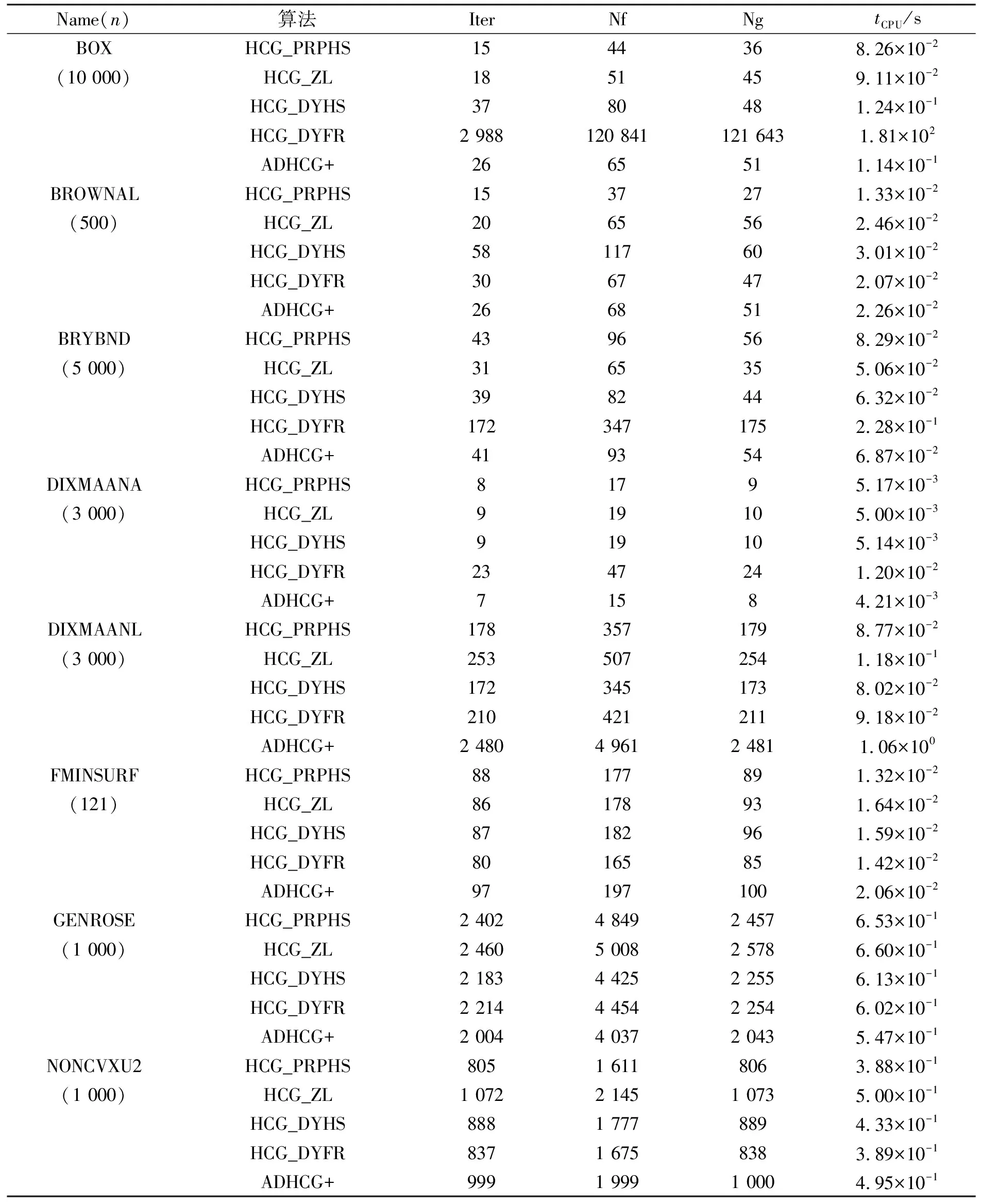
表1 算法的数值结果(部分)
由于算法求解CUTEst测试问题的数据量较大, 因此表1中仅列出部分数据, 以展示所得到的数据类型, 其中: Name表示测试问题在CUTEst测试环境中的名称,n表示问题的维数; Iter表示算法终止时的迭代次数; Nf表示算法达到终止准则时函数值被计算的次数; Ng表示算法达到终止准则时, 函数的梯度值被调用的次数;tCPU表示算法运行的CPU时间.
将算法求解CUTEst测试问题, 达到终止准则时的迭代次数, 函数值被计算的次数, 函数梯度值被调用的次数和算法运行的CPU时间作为评价指标, 利用Dolan等[17]提出的比较准则, 对算法分别就这4个评价指标的数据进行比较, 结果分别如图1~图4所示. 图1~图4中曲线表示算法求解测试问题效率的分布函数, 横轴表示算法求解问题的效率阈值, 纵轴表示在即定阈值下, 算法求解出的问题占总问题量的比例. 曲线越靠上, 该曲线所表示的算法越稳定, 曲线越靠左, 相应算法求解问题的效率越高.
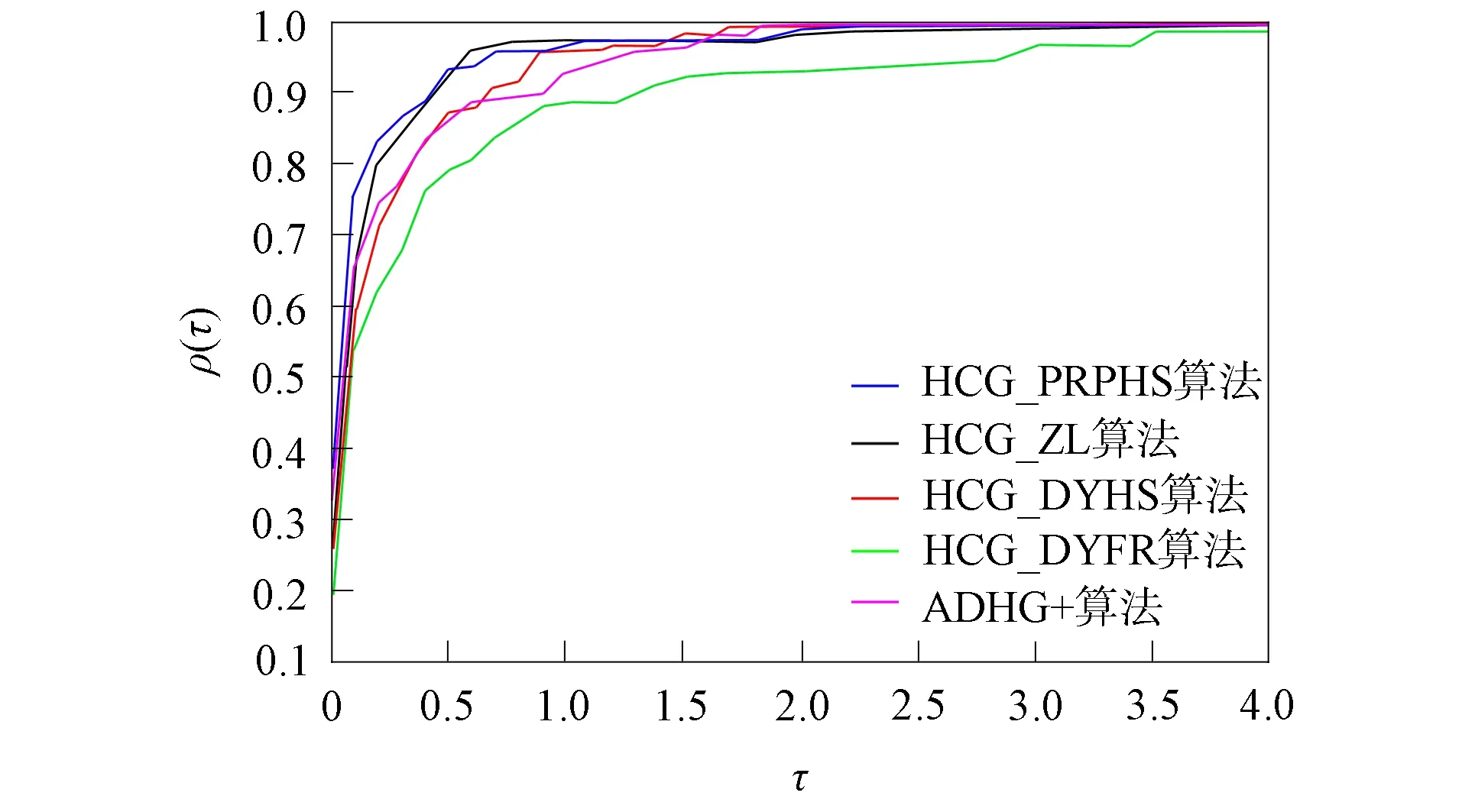
图1 不同算法基于迭代次数的比较Fig.1 Comparison of different algorithms based on number of iterations
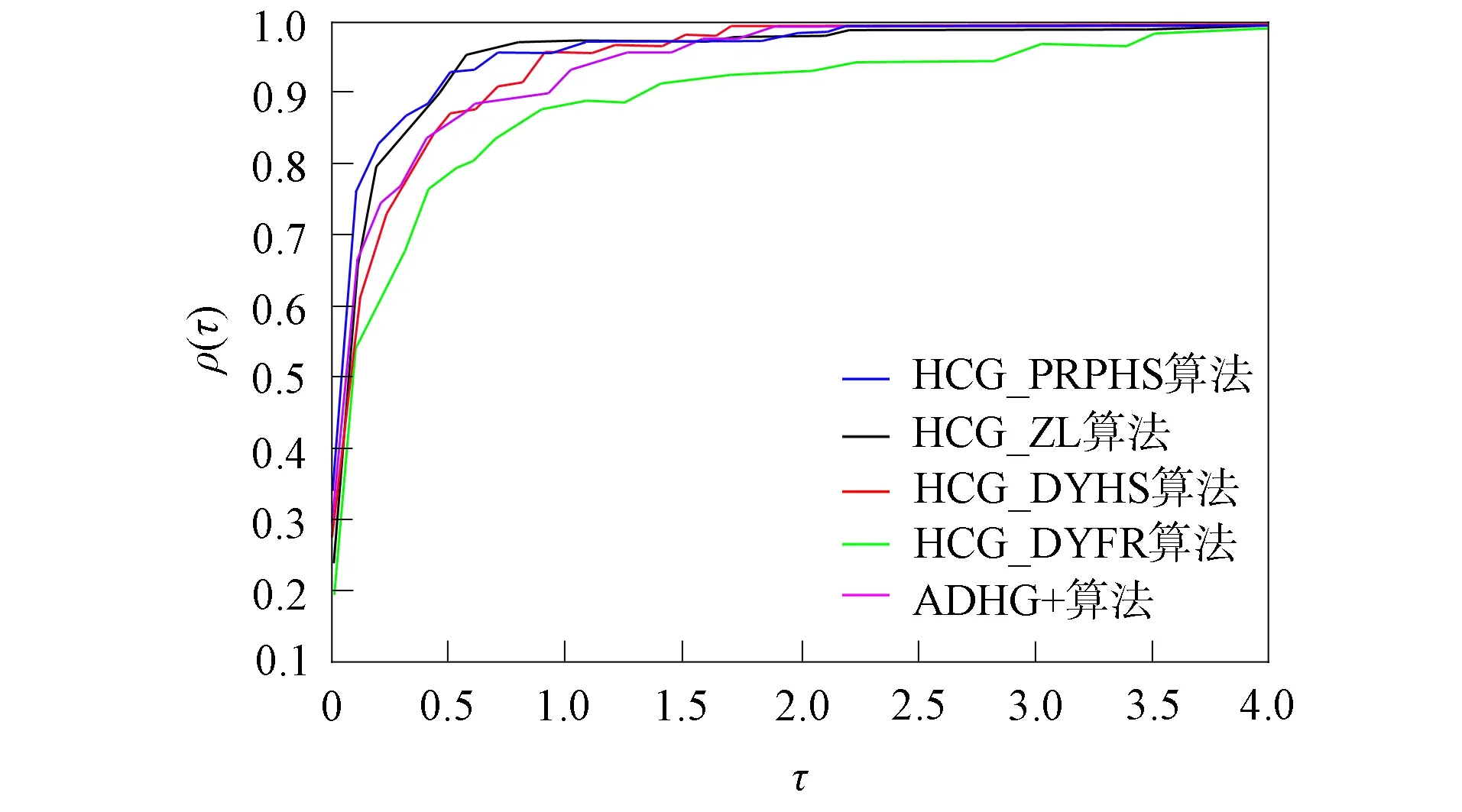
图2 不同算法基于函数值计算次数的比较Fig.2 Comparison of different algorithms based on function value calculation times
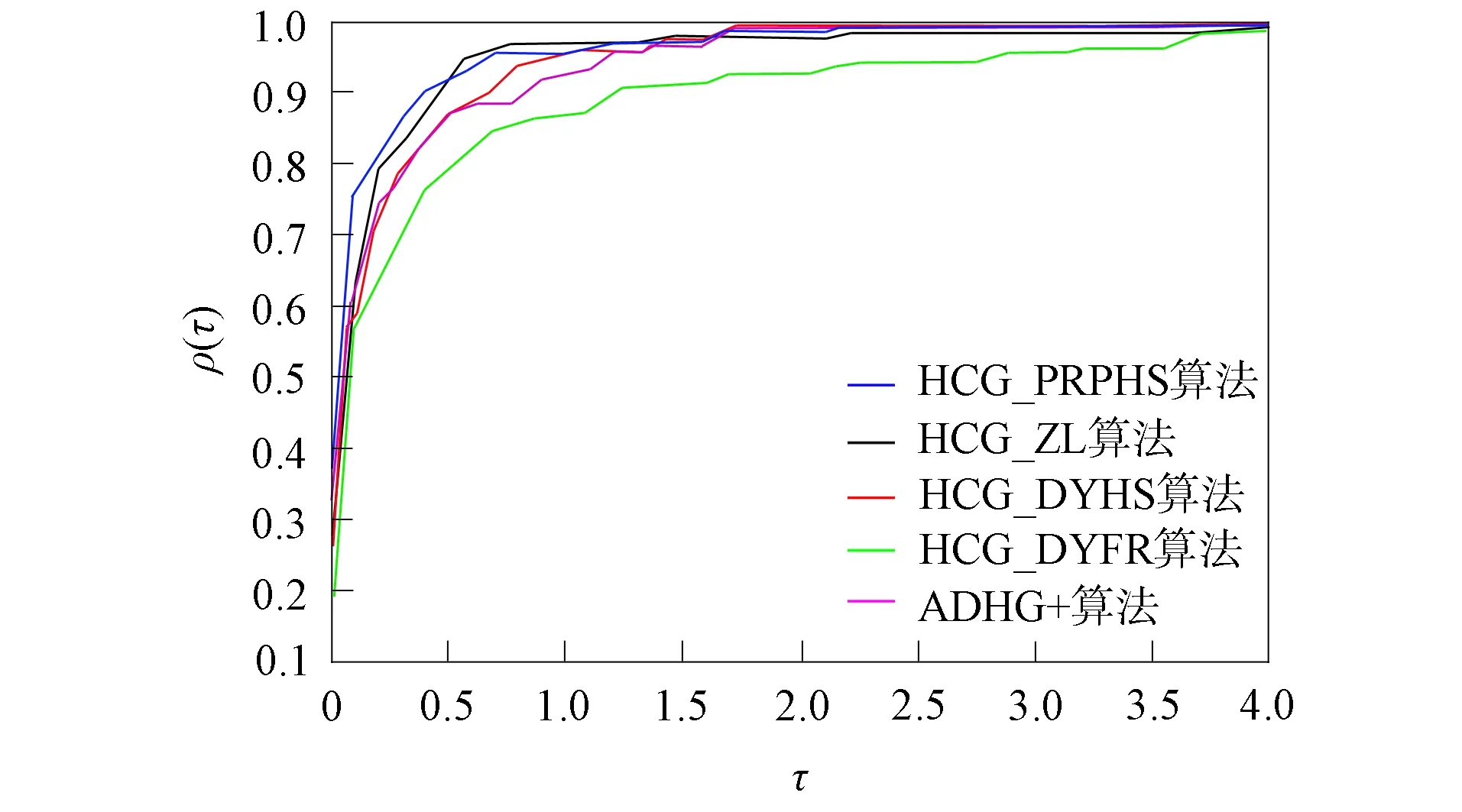
图3 不同算法基于梯度值计算次数的比较Fig.3 Comparison of different algorithms based on gradient value calculation times

图4 不同算法基于CPU运行时间的比较Fig.4 Comparison of different algorithms based on CPU running time
由图1~图4可见, 5种算法都能有效求解CUTEst测试环境中的无约束优化问题, HCG_DYFR算法的数值性能相对较差, 在效率和稳定性上均不及其余4种算法, 这是由经典的DY和FR算法本身所具有的数值特点决定的. 其余4种算法均可以认为是基于HS算法的正交型共轭梯度法, 继承了经典的HS算法良好的数值特性, 但数值性能又有所不同. HCG_DYHS算法和ADHCG+算法均是基于经典的DY算法和HS算法进行设计的混合型算法, 虽然设计思路不同, 但数值性能较相似, 从数值效果上看, 强于DYFR类算法, 但无论从函数值计算次数还是从梯度计算次数上看, 效率均略逊于HCG_ZL算法和HCG_PRPHS算法. HCG_PRPHS算法和HCG_ZL算法具有较强的可比性, 不同的是HCG_PRPHS算法同时凸显了经典的PRP算法和HS算法的数值性能优势.
综上所述, 本文通过138个CUTEst测试问题说明了基于PRP和HS的混合型正交共轭梯度法在运行效率和稳定性方面均具有优势, 为实际工程应用中共轭梯度法的选择提供了借鉴方向.
