光泵磁力仪原子气室无磁加热腔数值模拟与实验验证*

罗海军,覃 睿,潘海涛,罗 霞,李妍妍,郭 彬

(重庆师范大学 物理与电子工程学院 光电功能材料重庆市重点实验室,重庆 401331)

0 引 言

在光泵磁力仪系统中,无磁加热腔结构由具体加热方式决定。传统的交流电、间断电加热方式利用线圈或双绞线发热控制加热腔温度；这种电加热方式虽然加热速度快、温漂小、热分布均匀,但由于采用电加热方式的加热腔是由金属材料制成,会产生感应磁噪声并且线圈本身也会引入磁噪声。虽然张鹏等人[18]利用差分对的布线方法可抵消线圈引入的磁噪声,但无法消除金属加热腔中因磁力仪射频磁场作用而产生的感应磁噪声。Savukov I等人[19]利用激光对加热腔进行加热,实现气室的无磁加热,但激光加热造价高,对光功率的稳定性要求高；并且激光加热腔是由高热导率的无机非金属材料制作而成,提高了腔体设计的难度和成本。Huang Q[20]以及Seltzer S J等人[21]采用低成本的热气流无磁加热,弥补了电加热和激光加热的不足,但热气流加热的单向加热模式限制了气室温度的操作性。

因此,本文基于具有加热冷却双向模式的水流加热方式,提出了一种原子气室无磁加热腔结构。利用有限元数值分析方法,对无磁加热腔有限元简化模型进行了热特性分析。在理论分析和实验的基础上,给出了热特性参数和边界条件。最后,通过实验验证了模型的准确性,证实了所设计的加热腔符合气室的加热要求。

1 有限元建模

1.1 传热机理

几何结构相对较复杂的无磁加热腔中的传热仿真需要进行三维建模,而加热流道内涉及大量计算的三维流动和传热建模可以通过一维管道流方程来简化。其流动可以通过以下的动量和质量守恒方程来描述

(1)

(2)

式中u为管道中心线切向的平均热水流速度,A为管道横截面积,ρ为热水流密度,p为压力。式(1)右侧第二项描述了由于内部粘性剪切引起的压降；其中,fD为达西摩擦因子,用Churchill摩擦模型表示,公式如下

(3)

其中

(4)

B=(37 530/Re)16

(5)

从式(3)可知,fD不仅是管道表面粗糙度除以管道直径e/d的函数,也是流体属性、流动速度和几何的函数,可以通过雷诺数与热水流物理属性相关联。雷诺数表达式如下

Re=ρud/μ

(6)

式中ρ,u,μ分别为热水流的密度、流速、黏性系数,d为管道直径。

加热流道内的热水流传热可以用能量方程来描述

(7)

式中Cp为恒压热容,T为热水流温度,k为导热系数。右侧第二项表示管道内部流体摩擦产生的耗散热,但无磁加热腔加热流道长度较短,因此耗散热可以忽略不计。Qwall为热水流与无磁加热腔热交换的源项。

无磁加热腔内的热传导传热由傅里叶定律描述

(8)

式中T2为无磁加热腔的温度；Q为管道所在位置的线热源,通过热交换源项Qwall实现式(7)和式(8)的两种能量热平衡耦合。热交换源项Qwall通过管壁进行传热,表达式如下

Qwall=hZ(Text-T)

(9)

式中Z为管道周长,h为传热系数,Text为管道外部温度,Qwall作为管壁传热方程中的源项。管道外部温度Text为无磁加热腔的温度场,管道与无磁加热腔体的温度耦合在三维域中作为线热源来实现。源强度与管道热水流和无磁加热腔之间的温度场差成正比。传热系数h由水的物理属性和流动特性决定,可根据努塞尔数计算

(10)

式中k为水的导热系数,Nu为努塞尔数,dh为管道直径。对于层流流动,圆形管道的努塞尔数Nu为3.66,而湍流流动,努塞尔数为

(11)

式中Pr=Cpμ/k为普朗特数。从式(11)中可知,当流动为湍流时,努塞尔数为摩擦因子fD的函数。因此,结合式(3)、式(4)、式(5)可知,径向传热量会随着通道表面粗糙度增大而增加。

1.2 无磁加热腔结构

无磁加热腔主要是由加热外腔、加热内腔、隔热层组成,其结构如图1所示。对于加热内腔,在其内部预留了放置气室的空间并在内壁周围设计了4个放置温度传感器的位置,以便实时检测气室温度。在加热内腔内壁与外壁之间,设计出一条螺旋型水流加热流道,可以有效地使内腔与热水流进行热传导并均匀受热。为了尽量减少加热内腔与外界的热交换、降低加热内腔热量的流失、更好地使气室均匀受热,在加热内腔与加热外腔之间添加了热绝缘层。加热外腔的主要作用是巩固无磁加热腔内部结构,使热绝缘层与加热内腔贴合更紧密。在加热内外腔和隔热层的轴向方向设计了2个直径为20 mm的圆孔,作为泵浦光的传播路径。无磁加热腔的主要结构参数如表1所示。

图1 无磁加热腔结构

表1 无磁加热腔主要结构参数mm

1.3 无磁加热腔有限元模型

无磁加热腔几何结构复杂,若直接用有限元模型进行描述,将需要大量剖分单元,增加了计算难度,导致计算结果不收敛。因此,为了提高网格剖分和计算的效率,有必要对无磁加热腔模型结构进行简化。在加热腔体结构中,内腔盖、外腔盖和分离的热绝缘层的结构设计是为了实际中的加热腔能更好地装配。在有限元建模中,忽略装配因素,整合外腔体、内腔体以及热绝缘层；用直径为25 mm,高为28 mm,壁厚为1 mm的圆柱模型作为原子气室模型；气室内以直径为23 mm,高为26 mm圆柱模型代替原子气体；原子气室周围放置温度传感器的空间以建模填充。加热流道通过软件COMSOL Multiphysics中管道流接口将三维流问题简化为三维曲线进行建模。简化后的无磁加热腔模型如图2所示。图2中所示的无磁加热腔有限元模型是利用软件COMSOL Multiphysics在Intel®Xeon®CPU E5—2630 v4@2.20 GHz计算机上进行的自由网格剖分运算。

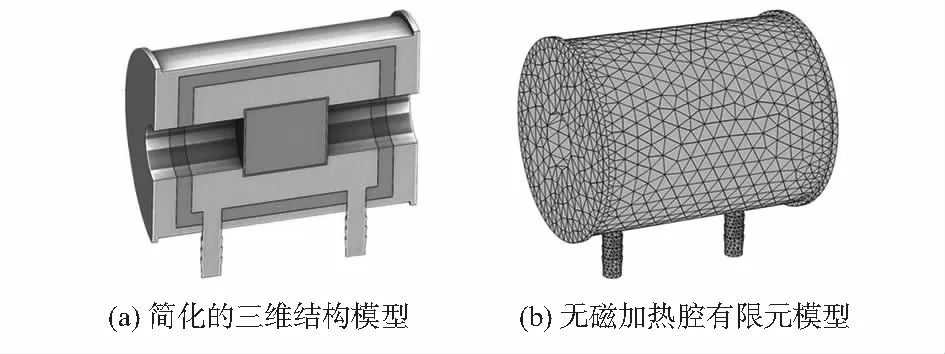
图2 三维结构和无磁加热腔有限元模型

1.4 有限元模型的初始和边界条件

在软件COMSOL Multiphysics中,非等温管流接口定义了加热流道内热水流流动的动量、能量和质量守恒的偏微分方程,固体传热接口定义了无磁加热腔的傅里叶热传导偏微分方程；可通过设置初始条件和边界条件,利用物理场接口求解无磁加热腔的温度分布以及热水流的流动、压力和温度并能完全耦合。偏微分方程中导热系数、恒压热容、密度等参数,来自如表2所示的无磁加热腔各部件材料的物理属性。

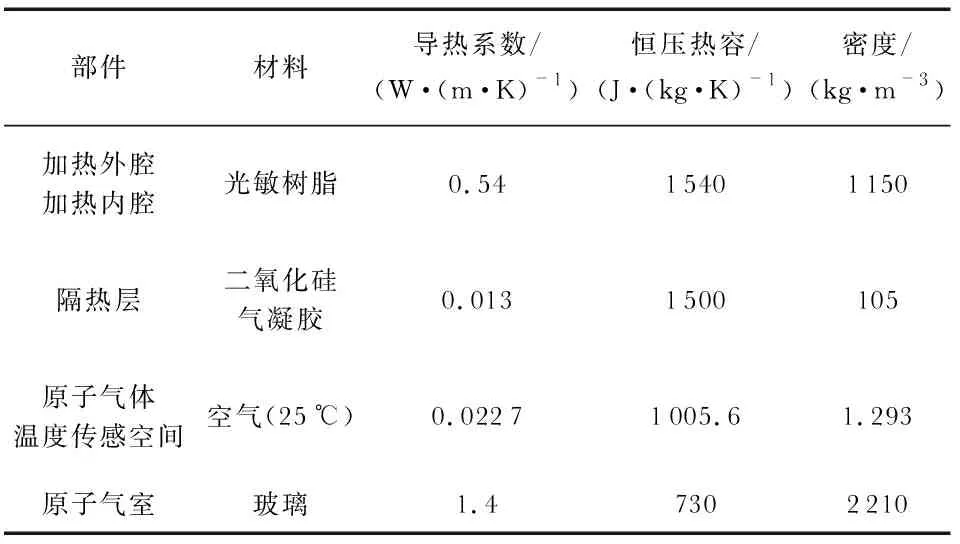
表2 无磁加热腔各部件材料物理属性

1.4.1 加热流道

根据加热流道内径等参数,令管道直径dj为4 mm,管道表面粗糙度e为0.046 mm,以确定流动方程中摩擦因子fD大小以及管道横截面积A。加热流道的流动方程与能量方程为一阶微分方程A,令其初始条件为

(12)

根据加热流道流动方向以及原子气室最佳温度范围,加入入口、热流出、壁传热边界条件,令入口温度Tin=45 ℃,管道体积流率qv=0.4 m3/s。

1.4.2 加热腔体

考虑实际中无磁加热腔体温度与室温相等,并且无磁加热腔表面与室内空气存在热交换,可通过热通量边界条件加以描述,则有

T2(x,y,z,0)=25 ℃

(13)

q0=h·(Text-T2)

(14)

式中 2 5℃为加热腔体初始温度,Text为外部室温25 ℃,T为腔体仿真温度,h为空气传热系数。

2 模型验证

为了验证无磁加热腔模型仿真结果的准确性与合理性,在实验室中进行了无磁加热腔的制作装配与测试。使用一套完善的水流温度控制系统对循环水进行加热控制；采用高分辨的NTC热敏电阻通过导热硅脂与腔体紧密贴合,分别对无磁加热腔内外7个测试点进行局部温度测量；并且利用上位机客户端对NTC热敏电阻测得温度数据进行长时间记录。所测得数据集用于表征无磁加热腔实际温度分布情况,并与加热腔模型的仿真结果作比较。NTC热敏电阻在无磁加热腔中分布的位置如图3所示。

图3 NTC热敏电阻在无磁加热腔中分布的位置

为了验证仿真模型的预测精度,列出以下两式计算仿真值与实测值之间的相对误差与相对偏差

Δ=|Tt-Ts|

(15)

(16)

式中Δ为仿真值与实测值之间的相对偏差,Ts为模型的温度仿真值,Tt为实际温度测量值,ξ为仿真值与实测值之间的相对误差。

假设室温为25 ℃,用稳态方法对无磁加热腔模型的温度场求解,腔体温度分布如图4所示。图中标注出了实际测量中7个测试点温度的仿真值。

图4 无磁加热腔温度分布

从图4(b)和图4(c)的温度分布情况可知,内腔温度分布较均匀,在44.3 ℃左右。因为加热流道入口热水流流动相对较缓慢,使传热更加有效,所以此处温度略高,约45 ℃。因内腔受热均匀的原因,原子气室内部温度分布较均匀；但测试点5和测试点6的仿真值为41.5 ℃左右,低于气室四周温度。其原因为在对原子气室仿真模型求解时,气室不但受到加热内腔的热传导,其底面和顶面还要与空气进行热交换,因此气室底面和顶面温度低于四周温度。而在实际的光泵磁力仪系统中,无磁加热腔前后级联了其它系统,没有空气与之产生热通量,所以气室底面和顶面的温度梯度可忽略不计。从图4(a)中可知,测试点7的仿真值为30.431 ℃,高于室温约5 ℃,低于内腔温度约15 ℃,这是因为热绝缘层隔热引起的较大的温度梯度。

在实验中,利用水流温度控制系统使无磁加热腔体中水温保持在44.2 ℃,并测得图3中不同测试点的温度上升数据如图5所示。

图5 水温为45 ℃时,无磁加热腔不同测试点的温升曲线

从图5中可以看出,测试点1～4的温度稳定在45 ℃左右,测试点5,6的稳定在41.5 ℃左右,测试7的温度稳定在29.7 ℃左右。图中温升数据的波动是由于水温受到外界的影响未能稳定在45 ℃造成的。表3中给出了,各测试点温度稳定后的实测值与仿真值之间的相对误差和相对偏差。其中最大相对偏差为0.735 ℃,最大相对误差为2.415 %,因此,无磁加热腔仿真模型的温度分布与实际温度分布几乎一致。

表3 水温为45 ℃时,各测试点的仿真值、实测值

为了进一步分析无磁加热腔的保温性,用瞬态方法求解加热腔仿真模型。记录加热腔在有、无热绝缘层时腔体自然冷却的仿真与实测数据,如图6所示。

图6 无磁加热腔自然冷却的降温实测与仿真数据

从图6中可知,实测降温数据与仿真数据较吻合；无热绝缘层加热腔的自然冷却速率明显比含热绝缘层加热腔要高；冷却到26 ℃,无热绝缘层加热腔需要5 400 s,而含热绝缘层加热腔则需要9 000 s。这是由于低导热系数的热绝缘层降低了内腔热量的发散速率,给无磁加热腔起到了保温作用。图7所示为水流升温时无磁加热腔温度的实测与仿真数据。从图中可知,当水温上升到为45 ℃时,无磁加热腔温度为31.5 ℃,温差为13.5 ℃,腔体温度不能较好的跟随水流温升速度,表明无磁加热腔导热性能不佳。

图7 水温从25 ℃到45 ℃时,无磁加热腔的温度变化

3 结 论

采用有限元方法研究了所设计的光泵磁力仪原子气室无磁加热腔的热性能,通过实验验证了无磁加热腔数值仿真结果的准确性。结果表明:热交换后的无磁加热腔温度分布均匀,能够使原子气室均匀受热；并具有良好的保温性,热量不易发散,令外部温度控制系统能够高效通过加热腔控制原子气室温度。由此说明,无磁加热腔符合光泵磁力仪原子气室的加热需求。但无磁加热腔导热效率不佳,不能及时跟随热水流的温度,增加了光泵磁力仪预热时间。对于这方面的改进,将在后续工作中完成。