面向异质基因数据的智能层次聚类算法研究

季姜帅，裴颂文，2

1(上海理工大学 光电信息与计算机工程学院，上海 200093)

2(复旦大学 上海市数据科学重点实验室，上海 200433)

E-mail：swpei@usst.edu.cn

1 引 言

癌症是威胁人类健康的主要疾病之一，常见的诊断与治疗方法有CT、放疗和化疗等，虽然有一定的效果，但患者在接受治疗过程中受到的辐射会产生一定的副作用.近年来，基因芯片技术飞速的发展，带来了许多蕴含巨大科学价值的数据，从基因层面上挖掘癌症的致病基因并提出针对性的治疗方法是一大趋势.聚类分析可以有效识别基因大数据背后的潜在结构和价值.如利用聚类算法对肿瘤相关基因表达数据进行分型，可以识别出在临床、病理等方面表现差异的肿瘤亚型，不同的亚型对应着不同的治疗方法，为临床科学研究提供新思路和新方法[1].

聚类分析是一种基于数据点之间相似度的无监督学习方法.目前，聚类分析已广泛应用于图像处理、模式识别、电力系统、统计学以及生物信息学等领域.陈叶旺等人致力于密度聚类算法研究，基于有效半径和密度热量，对DBSCAN、MeanShift、DPeak等进行改进，提出了DHeat算法，能自适应确定扫描半径[2]；之后进一步使用快速近似KNN算法检测所有类型相同的核心块、非核心块和噪声块，设计了一种快速合并核心块并将非核心点分配到合适簇以加速聚类过程[3].为了解决基于质心的聚类方法无法识别非各向同性的极其复杂数据的问题.陈叶旺等人提出了基于查找密度核的混合分散式算法DCore[4].Qaddoura等人使用基于距离矢量的选择操作迭代地考虑一个最近的点，提出了具有索引比的最近点算法NPIR，用于发现非球形簇的聚类[5].黄晓辉等人利用特征加权方法，提出了KICIC算法，通过在子空间内最大化簇中心与其他簇的距离进行聚类[6].

遗传算法采用自然进化模型，通过对进化过程中的种群，反复进行选择、交叉和变异等操作，模拟自然界中种群演变的过程，直到满足一定的条件才停止[7].虽然在整个进化过程中遗传操作是随机的，但它可以有效地根据已有的信息自适应地控制搜索的方向，找出最优解.由于遗传算法本身的结构决定了它可以很好地应用在基因表达量数据中.

近年来，遗传算法在生物医学中的应用研究越来越广泛.Toubiana等人通过逐渐增加性状与基因模块的子集之间的相关性来优化性状与基因模块的关系，提出了基于遗传算法的随机优化算法[8].刘鹏等人为了解决医学图像中的噪声问题，提出了基于遗传算法的网络进化方法，通过基于经验的贪婪探索策略和转移学习来加快进化过程[9].高楠等人将遗传算法与基因组排序相结合，以产生一种可以在有限的时间和空间内解决DCJ中值问题的新方法[10].

层次聚类算法输出最主要的部分是聚类树，其可以为研究分层聚类的结果提供直观的表现形式[11]，由于层次聚类的逻辑原理易于理解，通用性较好，具有准确的聚类结果并且可以根据一定阈值，自行选择在所需级别对聚类树进行“剪枝”操作以获得合适的聚类等特性，因此广泛应用于大数据挖掘中，特别是在生物信息学中应用更为普遍.

对于高通量测序得到的基因表达量数据，一般具有高噪声、高维度与非对称性等特点.虽然聚类是智能算法，但传统的聚类算法存在着易陷入局部最优解、易受噪声干扰和时空复杂度高等问题，在应用于基因表达量数据时不能有效准确地聚类.

基于以上问题，本文提出了一种基于改进遗传算法的层次聚类算法(HCIGA：Hierarchical Clustering of Improving Genetic Algorithm)，HCIGA融合了精英保留法与轮盘赌的选择算子，优化了适应度函数，采用了自适应交叉率和变异率，并引入小生境技术保持种群的多样性，提高算法的全局搜索能力，并在层次聚类中使用有序表来降低复杂度.最后分别用两组异质基因数据集验证算法的有效性.

2 HCIGA算法

2.1 相关理论

在层次聚类算法中，数据被逐层合并或者分解成一棵层次分明的聚类树.按照树的生成步骤可分为两大类：自顶而下的分裂式层次聚类算法和自底而上的凝聚型层次聚类算法.针对分裂式层次聚类算法计算复杂度高的问题，本文采用凝聚型层次聚类算法为研究对象.

对于基因表达数据来说，层次聚类算法的优点是通过设置不同的相关参数值，可以得到不同粒度水平上的多层次聚类结构；在聚类形状方面，层次聚类适用于任意形状的聚类；层次聚类算法可以方便地构建出一棵基因聚类树，充分反映基因之间相似性的关系.

虽然层次聚类算法在基因表达量数据中的应用有诸多优势，但层次聚类算法本身还存在着一些不足之处：聚类操作需要使用相似度矩阵，导致算法的时间和空间复杂度大，所以必须进行优化后才能在较大的数据集中使用；层次聚类的结果取决于上一个合并点或分裂点，下一次聚类会在前一次聚类基础之上继续进行合并或分裂，一旦聚类结果形成，已完成的聚类不能被撤消，簇间也不能交换对象，即层次聚类最大的缺陷就是不可逆性.因此选择合适的分裂或聚合点是层次聚类的关键.

2.2 HCIGA算法

现有常用聚类算法在某些通用数据集中能取得较为理想的聚类结果，但当应用于异质基因表达量数据集时，由于基因数据的非对称性以及分离度不明显，会导致聚类效果不佳.同时现有常用聚类算法仅基于统计学而很少考虑异质基因内部联系与患者预后效果，聚类结果不一定具备生物学研究意义.因此本文在遗传聚类算法中融合生物学分析，使HCIGA算法在异质基因表达量数据中具有生物学意义.

传统遗传算法虽然在初期能保持种群的多样性，但随着进化的逐步深入，多个个体易集中于某一极值点上，陷入局部最优解的陷阱.因此本文引入了小生境技术[12]，融合改进的遗传算法与凝聚型层次聚类，对异质基因表达量数据集进行聚类分析，解决基因数据的高维度、高噪声和非对称性问题，并获得较高的聚类精确度和较快的收敛速度.HCIGA算法的流程如图1所示.

图1 HCIGA流程图Fig.1 Flow chart of HCIGA

HCIGA先对基因表达量数据预处理，对基质细胞和免疫细胞计算肿瘤纯度得分，并通过Wilcoxon秩和检验进行差异分析，对筛选的差异基因进行层次聚类，利用适应度函数F(x)计算种群中所有染色体的适应度值，在未达到停止条件时：将适应度值降序排列，选择适应度高的优良个体组成新种群，对父代进行选择、自适应交叉和变异，通过排挤小生境策略不断更新种群.当种群满足终止条件时，将最佳染色体种群解码并利用改进的凝聚型层次聚类算法对样本进行聚类得到最佳亚型.

2.2.1 编码方式

基因表达数据是一个n×m维的实值矩阵M[xij]n*m，如图2所示，其中n代表基因的个数，m表示实验样本总数，行名一般用基因名称标注，列名为样本名称，矩阵中每个元素xij表示第i(1≤i≤n)个基因Gi在第j(1≤j≤m)个样本Sj中的表达量.

图2 基因表达矩阵示意图Fig.2 Schematic diagram of gene expression matrix

对于遗传算法编码方式的选择，综合考虑染色体基因的选择、交叉、变异等运算后，本文采用二进制编码方式，“0”表示未选择基因，“1”表示选择基因，因此种群个体可以编码为长度为n位的“0”和“1”字符串.采用这种编码方式可以大大提高效率，在解码时只需将“1”对应的基因挑选出来即可.

2.2.2 种群初始化

虽然随机初始化种群可以保证种群的多样性，避免种群陷入局部最优解，但在随机初始化种群的过程中，容易产生非法编码.因此，本文对种群的初始化加以限制：随机生成正整数a控制选取的基因数，10/n≤a≤n，其中n为差异表达基因数，a表示选取基因数，即随机将a个差异基因位置“1”，其余n-a个差异基因位置“0”.并利用凝聚型层次聚类随机生成k个初始中心.

2.2.3 适应度函数

适应度函数是控制种群遗传的重要部分，本文根据基因表达量数据的特点，综合考虑簇的规模和簇内外相似度，优化后的适应度函数F(x)如公式(1)所示：

(1)

其中ni为第i个簇内个体总数，n为种群内个体总数，k为簇的个数，Li为第i个簇内相似度，S为簇间相似度，α为平衡系数，用于平衡簇内与簇间相似度的比例，不同的数据集对应不同的α.

簇内相似度Li定义如公式(2)所示：

(2)

其中m为样本总数，xij为基因Gi在样本Sj中的表达量，Mi是第i簇基因的样本中心：

(3)

簇间相似度S定义如公式(4)所示：

(4)

其中σ为高斯常数，为了计算的方便，可以取2σ2=1，d2(Mi，Mj)，为簇样本中心Mi和Mj的距离.

在对样本进行聚类的过程中，若簇内相似度越大，且簇间相似度越小，则聚类的效果越理想.

2.2.4 遗传算子

选择算子：由于轮盘赌选择是随机操作，适应度值高的染色体也有被淘汰的可能性，为了解决这个问题，使最优个体被保留，本文设计了融合精英保留法与轮盘赌的选择算子，对所有染色体的适应度降序排列，前5%的优秀染色体直接遗传给下一代，后95%的染色体参与轮盘赌选择，以此来保持种群中优良个体.

交叉概率Pc和变异概率Pm是影响遗传算法性能的关键，而Pc和Pm难以精确设定.本文采用了自适应策略根据种群的适应度来动态地调整Pc和Pm.

交叉算子：由于单点交叉和多点交叉的搜索空间较小，同时还可能会引起位置的偏差，本文采用效果更好的均匀交叉作为交叉算子，可以有效提高算法的局部搜索能力.

主要操作如下：

1)从种群中随机选取一对交叉的父染色体.

2)随机生成与染色体等长的“0”和“1”掩码串，若掩码当前位为“0”，代表由父染色体2提供变量值，若掩码相应位为“1”，则代表由父染色体1提供变量值.

改进后的自适应交叉概率Pci如公式(5)所示：

(5)

其中Pci为第i代的交叉概率；Pc0为初始交叉概率；k1为交叉比例系数；Geni为当前执行第i代遗传操作；Genmax为最大遗传代数；Fc为两个待交叉染色体适应度的平均值；Fa为种群适应度的平均值.

变异算子：由于本文采用的是二进制编码方式，在进行基因位变异运算时可以轻松实现.具体过程为：从种群中随机抽取一条染色体，将其以自适应变异概率Pmi改变某位值，以此扩大算法搜索空间.

改进后的自适应变异概率Pmi计算公式如式(6)所示：

(6)

其中Pmi为第i代的变异概率；Pm0为初始变异概率；k2为变异比例系数；Geni为当前执行第i代遗传操作；Genmax为最大遗传代数；Fm为待变异染色体适应度值；Fa为种群适应度的平均值.

2.2.5 小生境技术

为了提高种群的多样性和全局最优解搜索能力，本文在遗传算法中引入基于排挤机制的小生境技术.在小生境遗传算法中采用海明距离Hij来表示染色体Ri和Rj之间的相似度,如公式(7)所示：

(7)

其中rik表示染色体Ri的第k位.很明显，当Ri和Rj之间的海明距离Hij越小，两染色体之间的相似度越高，当Hij小于某一阈值γ时(γ为某一很小的正整数)，染色体Ri和Rj即属于同一小生境，此时比较两者的适应度值，对适应度值小的染色体设置惩罚函数F′(x)=0.6*F(x)，以此降低其适应度，减小其在子代中的遗传概率.经过排挤小生境操作后，适应度在阈值γ内的两个染色体，仅需保留适应度较高者，极大地提高了种群的多样性.同时在种群个体数量恒定的情况下，使染色体在整个解空间内分散开来，增强了全局搜索能力，从而解决局部最优解的问题.

2.2.6 改进的层次聚类算法

由于传统的层次聚类算法的复杂度达到了O(n3)，在高维数据集中效率低下，根本原因是传统层次聚类算法在每次合并两个相似度最大的簇后需要重新生成相似度矩阵，这大大消耗了时间与资源.本文利用有序表对各基因相似度进行降序存储，提高层次聚类算法的效率.

在相似性度量方面，通用的聚类算法采用欧几里德距离作为样本间相似性的度量，这在非基因表达量数据集是可行的，但由于多数情况下，基因表达量是实验样本与对照组之间的Ratio值，欧式距离无法准确刻画基因间的相似度.所以本文选用皮尔逊相关系数作为基因间相似性的度量.

设在n×m维的基因表达量矩阵M中，存在两个基因组向量Ga=(xa1，xa2，…，xam)和Gb=(xb1，xb2，…，xbm)，1≤a≤m，1≤b≤m，xij表示第i(1≤i≤n)个基因Gi在第j(1≤j≤m)个样本Sj中的表达量.则基因Ga与Gb的相似度可以定义为Sab：

(8)

(9)

(10)

在相似性度量设计方面，本文选择均链接法，综合考虑了两个类间各基因表达值之间的相关性，从而可以有效避免类连锁现象.

3 实验评估及结果分析

本文实验验证的开发环境为PyCharm 2020.2.1，数据预处理软件为RStudio 1.2.1335.

3.1 实验数据集

为了综合评估本算法的性能，本文设计了两类实验，第1类为使用经过实验验证并且带标签的4组基因表达量数据集：脑肿瘤[13]、肺癌[14]、肾脏癌[15]和乳腺癌[16]，用于HCIGA精确度的评估，4组数据集的属性描述如表1.第2类为使用从癌症基因组图谱官网(TCGA)中获取不带标签的HNSC数据集进行聚类分析.从TCGA数据库中下载的HNSC数据集包括19645个基因，502个肿瘤样本和44个正常样本，以及528例临床样本.

表1 外部标准数据集参数Table 1 Parameters of external standard data sets

3.2 数据预处理

由于基因表达量数据的测量条件不同，各样本之间会存在一些差异，且并不是所有的基因组都与疾病的产生存在影响，所以在实验之前必须对数据进行清洗.

对于存在少量缺失值的样本，本文采用KNN填补缺失表达量；若缺失值较多或表达量为负值的基因样本则直接删除；使用RMA和分位数归一化分别建立这些芯片矩阵数据集的基因表达水平，以获得每个基因和样品的表达值[17]，并对基因表达量数据进行标准化.利用ESTIMATE[18]对肿瘤样本进行打分，并根据得分的中位值，将肿瘤样本划分为高得分组和低得分组.本文使用显著性分析[19]检测差异表达基因，利用Wilcoxon秩和检验，设置阈值|logFC|>1且FDR<0.05进行差异基因过滤.

遗传算法部分重要实验参数汇总见表2.

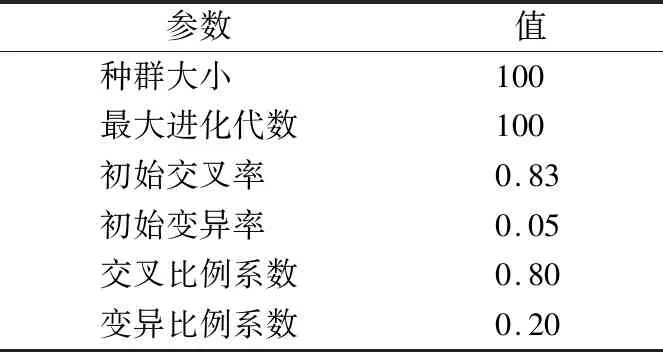
表2 主要实验参数Table 2 Main experimental parameters

3.3 实验结果与分析

3.3.1 外部指标性能度量

本文使用经典层次聚类算法AGNES、遗传K-Means算法GKA、DPeak算法、谱聚类算法和改进遗传层次聚类算法HCIGA在4个带类别标签的标准数据集(Brain Cancer、Lung Cancer、Renal Cancer、Breast Cancer)进行聚类分析，经过10次重复独立运行，得到五种算法在各数据集中平均聚类准确率，如图3所示.

图3 5种算法在4个数据集中正确率的对比Fig.3 Accuracy of the five algorithms in the four data sets

由图3可以看出AGNES在4个数据集中聚类精度都是最低，GKA和SC算法的聚类精度在Brain Cancer和Breast Cancer数据集中效果相当，但低于HCIGA和DPeak算法，而DPeak算法在Renal Cancer数据集中聚类精度不佳，低于GKA、谱聚类算法和HCIGA算法，仅优于AGNES算法，HCIGA算法在Brain Cancer等4个数据集中的聚类精度均为最高，聚类效果最佳.

根据第2节HCIGA算法分析部分，计算肿瘤纯度得分的时间可以忽略不计，相应的时间复杂度主要包括遗传算法和层次聚类两个阶段.设m为种群大小，n为染色体长度.在遗传操作阶段，初始化种群的时间可忽略不计，适应度函数计算的时间复杂度为O(mn)，在选择操作中，主要采用的是轮盘赌，在最坏的情况下需要遍历所有对象，因此时间复杂度为O(m2)，在交叉和变异操作阶段的时间复杂度均为O(m)，为了提高算法的全局搜索能力，引入小生境技术增加了一定的时间复杂度O(m).在聚类操作阶段，采用有序表结构代替每次重复的计算相似度矩阵，可使聚类操作的时间复杂度降至O(n2)，故算法HCIGA的时间复杂度为O(m2+n2)，稍逊于DPeak等主流聚类算法的时间复杂度O(n2)和GKA的O(m2+nkt)，但优于谱聚类的O(n3)，且聚类精度对比于另外4种算法有所提升.

图4 5种算法在4个数据集中RAND指数折线图Fig.4 Five algorithms in four data sets of RAND index line graph

3.3.2 内部指标性能度量

TCGA-HNSC数据集无模型给定的簇划分，因此无法使用外部指标来衡量算法模型的性能，本文选用了收敛速度与生存分析作为HCIGA有效性的内部评价指标.

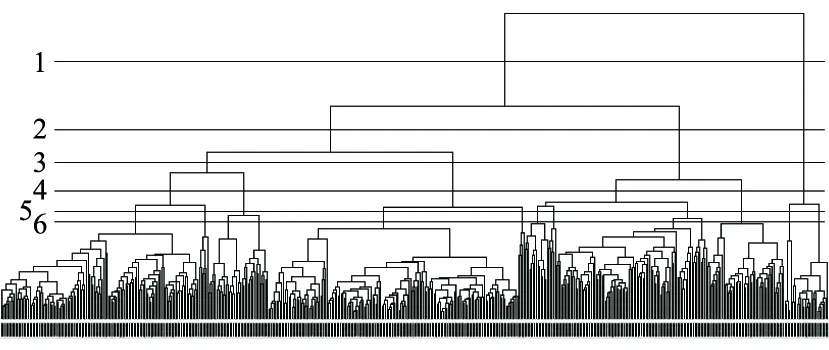
图5 HNSC数据集的聚类树Fig.5 Clustering tree of HNSC data set

对聚类个数的确定是影响聚类结果的关键因素.本文将HCIGA在HNSC数据集中得到的聚类树进行剪枝操作[20]，如图5所示，选取聚类数K为2、3、4、6、11、13这6种方案，并通过Silhouette指数对这六种方案的聚类数评估，Silhouette指数见表3.

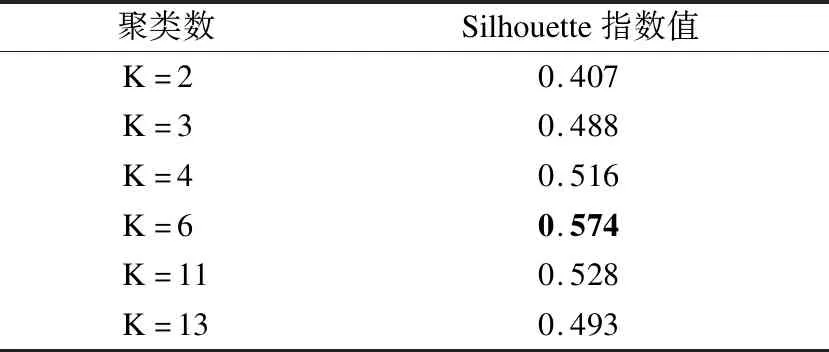
表3 各聚类数的Silhouette指数值Table 3 Silhouette indices of each clustering number

Silhouette指数值能很好地反应聚类类别的优劣，最大值对应着最优划分，由表3可以看出，当聚类数K=6时，所对应的Silhouette指数值最大，因此最终确定将聚类结果划分为6簇的方案.

在收敛速度评价指标方面，HCIGA与GKA的收敛速度曲线如图6所示，HCIGA在运行到第30代左右时，适应度值已基本达到最优；而GKA在第50代附近才取得最优适应度值，由此可见，HCIGA的收敛速度明显优于GKA算法.

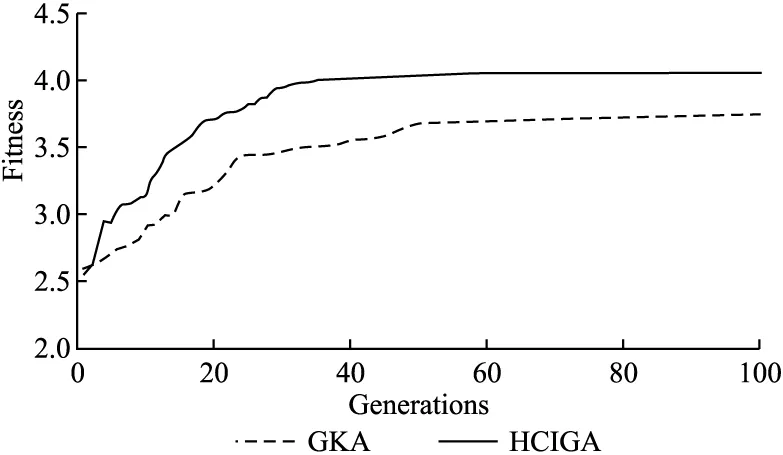
图6 HCIGA与GKA收敛速度Fig.6 Convergence rates of HCIGA and GKA

针对TCGA-HNSC的生存分析，如图7所示，可以分别绘制出HNSC 6种亚型的总体生存曲线，图示6条生存曲线走势各不相同，随着生存时间的推移，病人的存活率逐渐下降，亚型间的p值为6.98e-03小于0.05，这表明6种亚型的生存曲线具有统计学价值，即本算法聚类后的亚型结果与生存密切相关，可以很好地区分HNSC亚型.

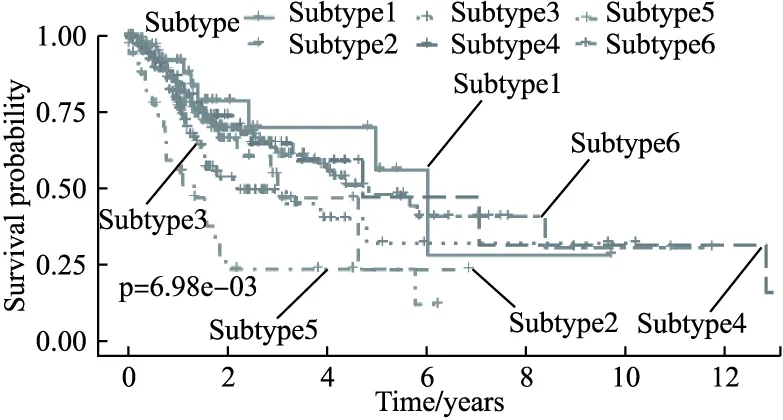
图7 各亚型间生存曲线图Fig.7 Survival curves among subtypes

4 结 论

随着高通量测序技术的蓬勃发展，基因数据井喷式增长，为了有效处理基因表达量数据，聚类分析作为一种无监督数据分析方法，成为基因研究的重要手段之一.本文在凝聚型层次聚类算法的基础上结合ESTIMATE评分体系、差异分析以及改进遗传算法，提出面向异质基因数据的智能层次聚类算法HCIGA.

本文将HCIGA在4个带类别标签数据集上的聚类精度与AGNES、GKA、DPeak以及SC算法进行对比，结果表明HCIGA的聚类精度在4个数据集中均为最高.本文并将HCIGA应用于TCGA数据库中无类别标签数据集HNSC，通过收敛速度以及生存分析等方法证明，HCIGA较GKA在收敛速度上取得明显提升，且利用HCIGA在HNSC中识别的6种亚型具有统计学意义和生物学价值.