基于扩展卡尔曼滤波和初等变换的结构参数和荷载识别研究
2022-08-29童倬慧贺佳
童倬慧,贺佳
(湖南大学 土木工程学院 建筑安全与节能教育部重点实验室,湖南 长沙 410082)
土木工程结构在服役期间受各种因素的影响,可能出现损伤,而结构损伤的发生、发展可以通过结构参数的变化(如刚度、阻尼)得到体现。因此,利用参数识别方法获取结构参数,有利于判断结构状态和评估工作性能。根据数字信号处理方式的不同,系统识别方法可分为3类:频域、时域和时频域方法[1-4]。频域方法主要基于结构模态参数,如频率、振型等展开识别,此类方法能较好的反映结构的整体状态,但是往往对于局部损伤不敏感。时域方法直接利用时域数字信号以及各种优化算法开展参数识别,包括最小二乘估计、EKF、深度学习方法等等。时频域方法则通过各种变换,如小波变换、希尔伯特变换等,利用时域和频域的联合信息开展参数识别。由于本文提出的是基于EKF 的参数识别方法,因此,以下重点关注基于EKF 的时域方法。EKF 方法从系统状态方程出发,将待识别的结构参数引入状态向量,利用泰勒级数进行线性化处理,并通过计算增益矩阵,对扩展的状态向量进行最小方差估计。目前,已有许多学者开展了基于EKF 的参数识别研究。例如,利用自适应因子,YANG 等[5-6]提出了基于EKF 的时变参数识别方法。LⅠU 等[7]提出了结合EKF和无迹卡尔曼滤波(UKF)适用于强非线性系统的两步识别方法。ZHANG 等[8]将l1范数正则化引入EKF 方法,提出了复杂结构的局部损伤识别方法。HUANG等[9]在ZHANG基础上将l1范数正则化改为lp范数正则化,减少了识别所需观测量。齐梦晨等[10]利用EKF 和全局迭代实现了免模型识别结构非线性恢复力。XU 等[11]利用EKF 和多项式拟合同时识别了结构非线性恢复力和结构质量。XⅠAO 等[12]提出了基于自适应EKF 的轨道不平顺及高铁桥梁频率识别方法。虽然以上方法均能实现结构参数的有效识别,但是均需已知作用于结构的外部激励,这从某种程度上限制了方法的普适性。因此,一些学者进一步开展了基于EKF 的未知激励下的结构参数识别研究。例如,基于全局迭代EKF 算法,XU 等[13]提出了子结构参数和荷载识别方法。EFTEKHAR 等[14]构造了未知外激励的状态方程,采用两阶段EKF 方法识别了未知外激励和结构状态。LEⅠ等[15]运用整体卡尔曼滤波法(GEKF)识别未知地震作用下的结构参数。LⅠU等[16]提出了一种模态EKF 算法,识别了结构参数和外荷载。LEⅠ等[17]提出了一种基于EKF 的非线性恢复力免模型识别方法。HE 等[18]通过引入投影矩阵,提出了基于EKF 的结构参数和荷载识别方法。利用子结构理论,HE 等[19]进一步将以上方法应用于子结构参数和边界力识别。以上提出的未知激励下的结构参数识别方法,计算过程相对较为复杂,对未知外激励进行最优估计时,都基于最小二乘原理。不同于以上方法,本文在理论上提出了一种相对清晰直观的方法,即通过引入初等变换矩阵将未知外激励所在的方程进行消元,得到不含未知外激励的系统观测方程组,进而通过EKF 识别结构参数,并进行系统状态估计,最后通过状态方程获取未知外激励。该方法可以有效缩减在计算后验估计的状态向量时,对应方程组的维度。方法的推导过程具体介绍如下,并通过线性和非线性数值算例验证了该方法的有效性。
1 理论推导
对于有m个自由度,n个待识别结构参数和r个未知外激励的结构而言,其运动平衡微分方程为:
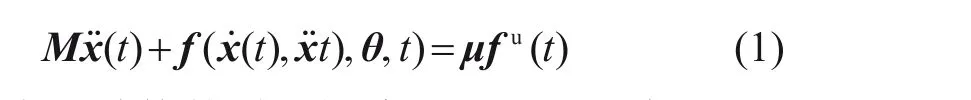
其中,M表示结构的质量矩阵,这里假设为已知;
引入2m+n维的状态向量Z来表示结构状态:
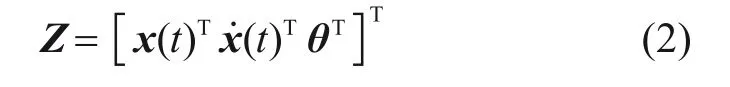
式(1)可以进一步写成:
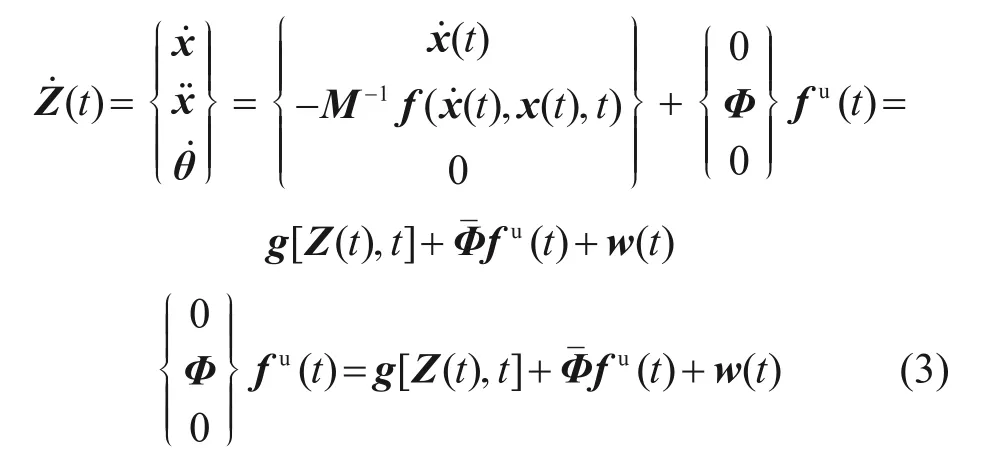
其中:
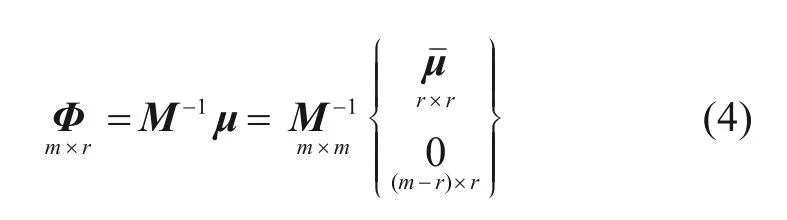
w(t)表示系统噪声向量,设为均值为0 的白噪声,其协方差阵E(w(t)w(t)T)=Q(t)。表示影响矩阵μ中与未知外激励直接相关的r×r维子矩阵。
基于EKF 原理,系统状态的先验估计可以表示为:
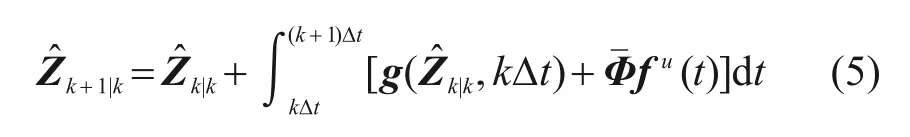
一般而言,加速度信号较容易获取,且相对可靠,因此,本文假设实测部分加速度,观测点个数设为l,则离散化后的观测方程可表示为:
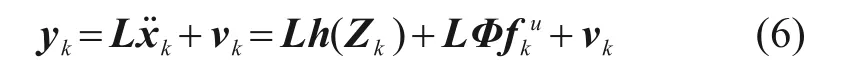
其中:yk表示t=k×Δt时刻实测的l个结构加速度响应。L表示与加速度传感器位置有关的(l×m)维观测矩阵,vk表示测量噪声,这里假设均值为0 的高斯白噪声,其协方差矩阵。
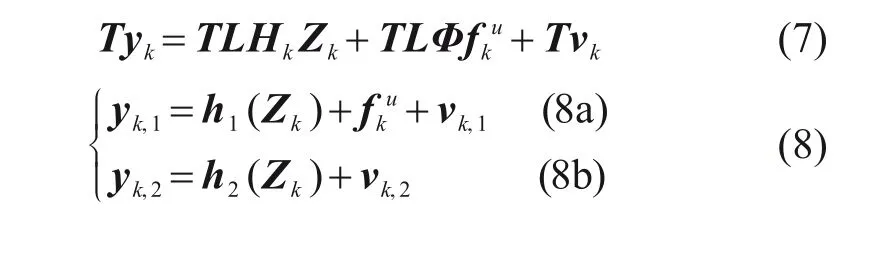
可以看出,在观测方程(6)中,将未知外激励系数矩阵LΦ左乘初等行变换矩阵T,可使得未知外激励向量的系数矩阵转化成行最简型矩阵:
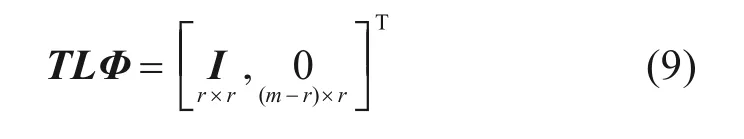
Matlab 中可以通过rref 函数根据Gauss-Jordan消元法找到矩阵行最简型,从而求出用于消元的初等行变换矩阵T。
不难看出,式(8b)中不含未知外激励,因此可以采取EKF,利用分离后的观测方程式(8b)和式(5)对Zk进行识别,假设式(8a)中观测噪声Rk,2。
根据HE 等[18]推导出的先验误差协方差矩阵Pk+1|k,可得
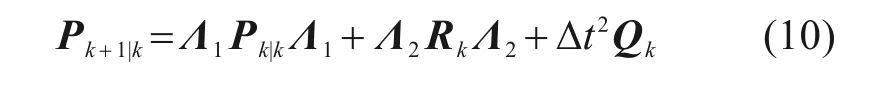
其中:
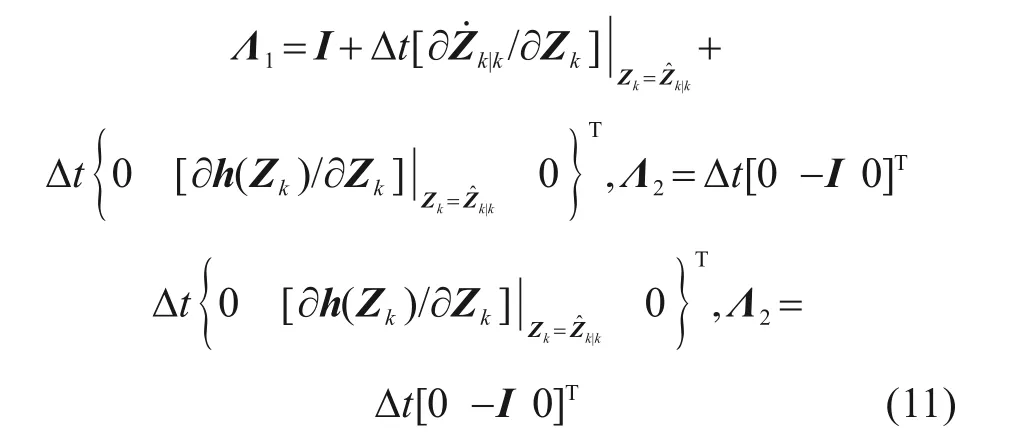
根据EKF 原理,系统状态的后验估计值需以其先验估计值为基础,同时考虑观测值与估计值之间的偏差,这里采用的第k+1 步测量值为不含未知外激励的yk+1,2,则
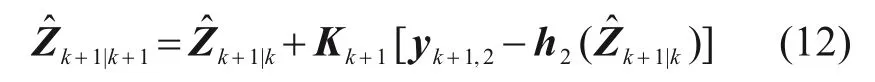
其中:Kk+1表示EKF增益矩阵,可由下式求得:
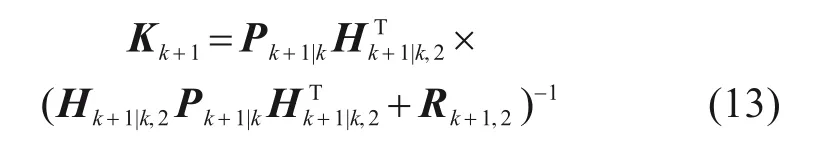
此时,系统的后验估计误差协方差矩阵可由下式计算得到:
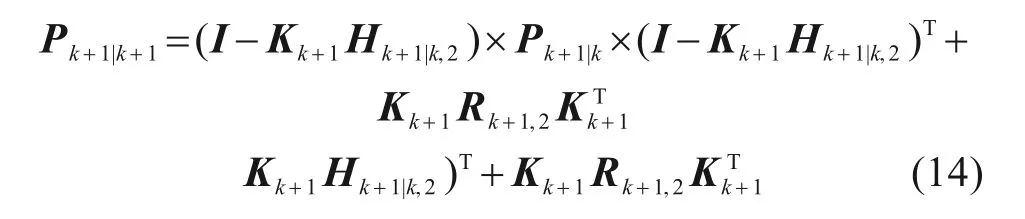
基于以上获取的系统状态的后验估计值,作用于结构的未知外激励未知外激励可由下式求得:
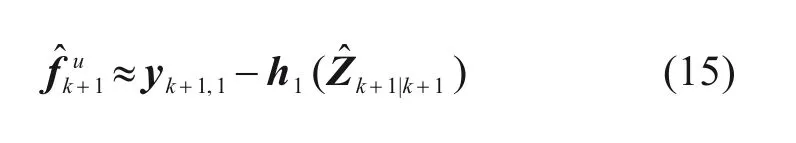
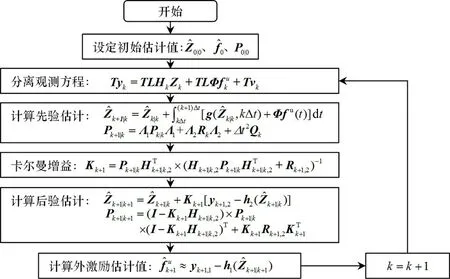
图1 识别算法流程图Fig.1 Flow chart of proposed approach for identification
2 数值算例
2.1 两层剪切型模型
为了验证本文提出方法的有效性,首先考虑2层剪切型结构。结构质量m1=m2=200 kg,各层刚度k1=k2=150 kN/m;采用瑞利阻尼构造阻尼矩阵,即C=α1M+α2K,这里取α1=0.73,α2=9.8×10-4。在结构顶层作用随机外激励,相应的结构响应根据状态空间法计算求出,计算的时间步长为0.001 s。假设观测加速度响应,考虑5%的噪声影响。系统噪声协方差矩阵R=I,观测噪声协方差矩阵Q=10-4I,待识别的结构参数为结构各层刚度ki(i=1,2),瑞利阻尼系数α1和α2,其初始值均假设为对应真实值的50%。
利用本文提出的方法,结构参数识别结果如表1所示。可以看出,本文提出的方法可以有效识别结构参数。为进一步考察参数的收敛情况,图2给出了部分参数的识别结果,为便于清晰显示其收敛情况,图中采用了不同比例的时间坐标。不难看出,各参数可以快速、稳定地收敛于真实值附近。由于篇幅限制,这里仅给出了部分参数的收敛结果。除了能有效识别结构参数以外,本文提出的方法还可以识别作用于结构的未知外激励,其识别结果如图2(c)所示,为便于清晰比较,图中仅给出了9~10 s 的识别结果。从图中可以看出,荷载识别值与真实值吻合得较好。
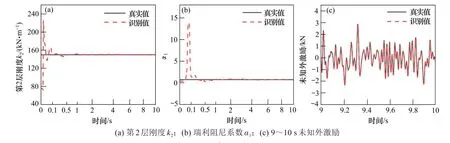
图2 2层剪切型结构参数和未知外激励识别结果Fig.2 Ⅰdentification of unknown excitation and parameters of the 2-floor shear structure
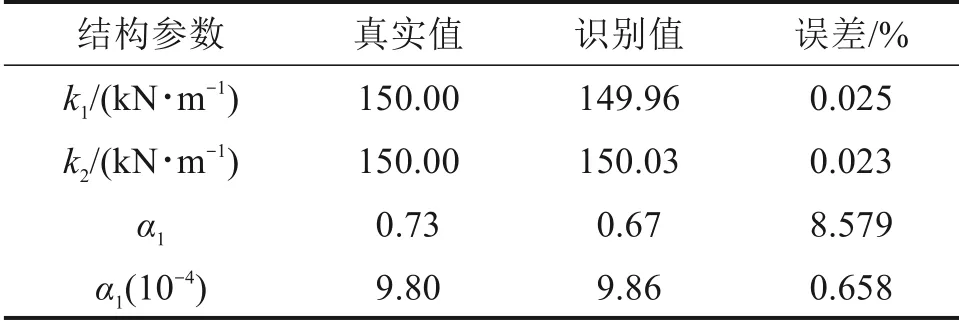
表1 2层剪切型结构参数识别结果Table 1 Ⅰdentification of the 2-floor shear structure
2.2 平面桁架模型
为了进一步验证算法的可行性,本节以一个平面桁架结构为例,如图3 所示。桁架参数取值为:水平杆长2 m,斜杆长 2m,各杆横截面面积S=2×10-4m2,材料弹性模量E=2×108Pa。采用一致质量矩阵来模拟结构的质量分布,结构阻尼采用瑞利阻尼假定,其阻尼系数为α1=6.15,α2=1.46×10-4。为模拟损伤,这里假设6 号和7 号杆件的刚度分别退化了15%和5%。在结构4 号节点的竖直方向施加随机激励,对应的结构响应根据状态空间法求出,计算的时间步长为0.001 s。假设观测第1,4,5,7,8 和9 个自由度上的加速度响应,并考虑5%的观测噪声影响。待识别的结构参数为各杆件的刚度,类似的,系统噪声协方差矩阵R=I,观测噪声协方差矩阵Q=10-4I,初始值均取对应真实值的50%。
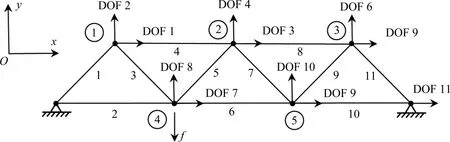
图3 平面桁架结构Fig.3 Planar truss structure
运用本文提出的方法,结构参数识别结果见表2,由表可见,各参数识别结果误差较小。图4给出了部分参数的收敛情况,可以看出,待识别的参数能够快速、稳定地收敛于真实值附近。同样地,本文提出的方法还可以有效识别作用于结构的未知外激励,如图4(c)所示。图中仅给出了5.0~5.5 s 的识别结果,很明显,识别值与真实值吻合得较好。
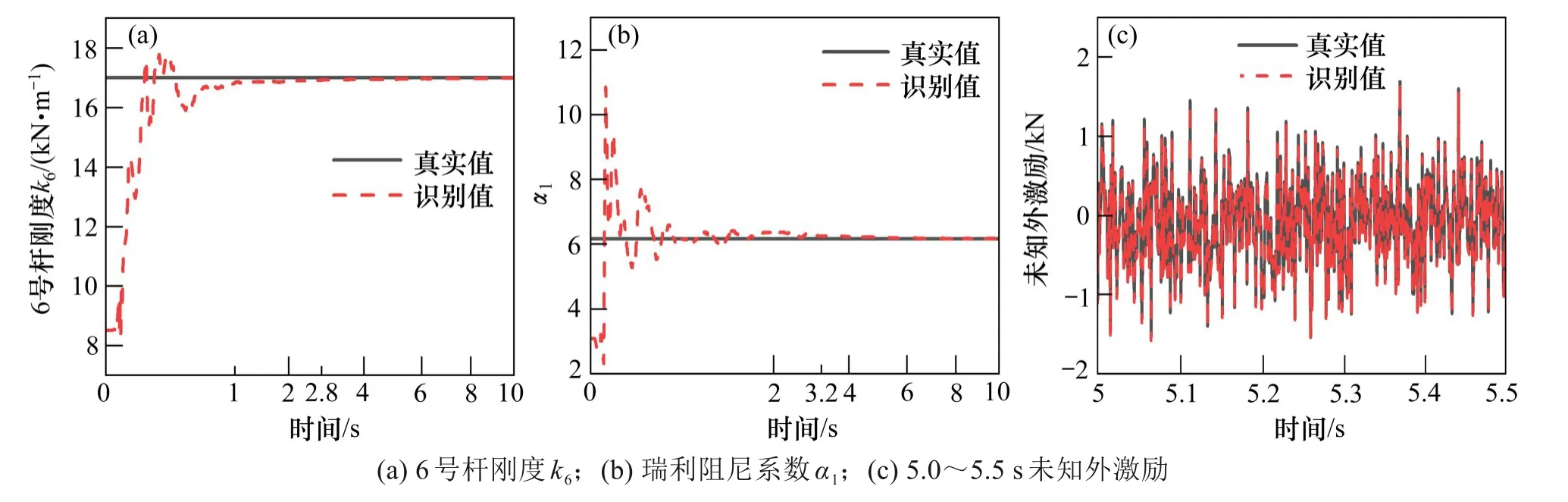
图4 平面桁架结构参数和未知外激励识别结果Fig.4 Ⅰdentification of unknown excitation and parameters of the planar truss structure
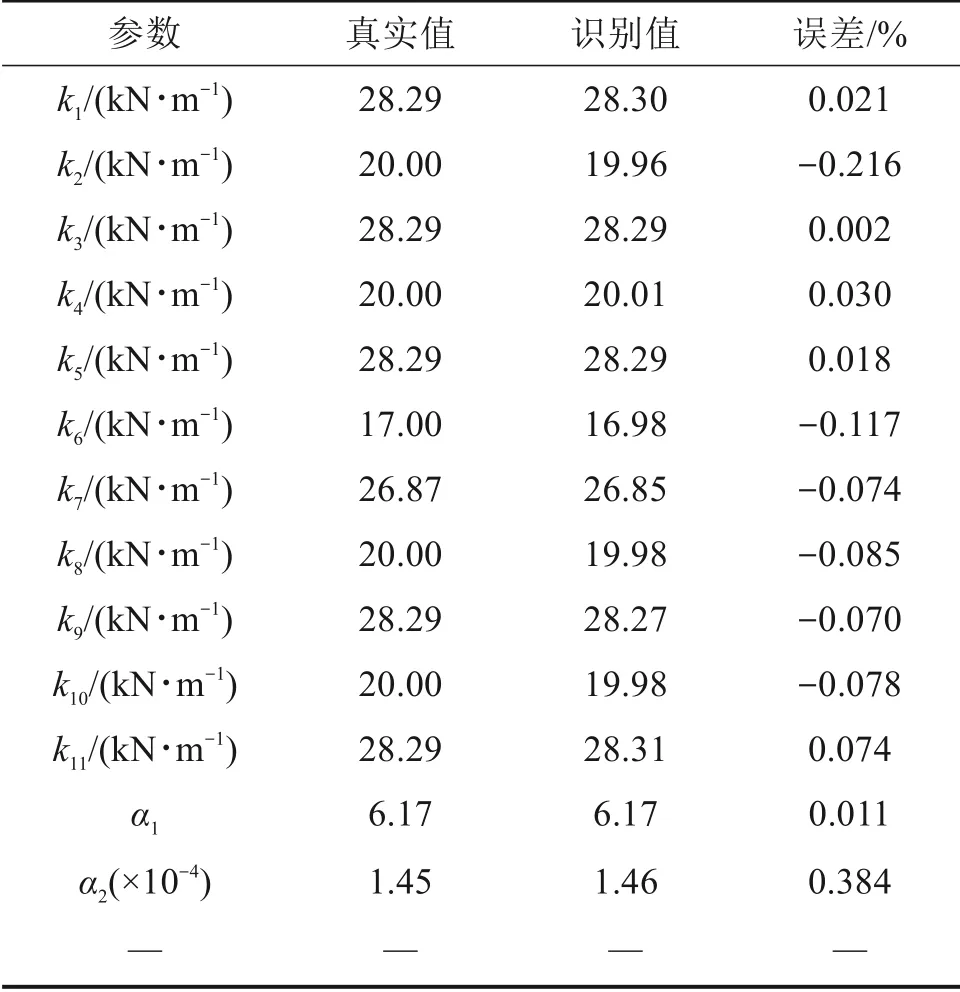
表2 平面桁架结构参数识别结果Table 2 Ⅰdentification of parameters of the planar truss structure
2.3 装有Dahl模型的非线性状态结构
为了讨论本文提出的算法在非线性系统识别中的有效性,本节考虑一个底层安装有MR阻尼器的5 层剪切型结构,如图5 所示。这里,采用Dahl模型来描述MR 阻尼器的非线性恢复力[20],如下式所示:
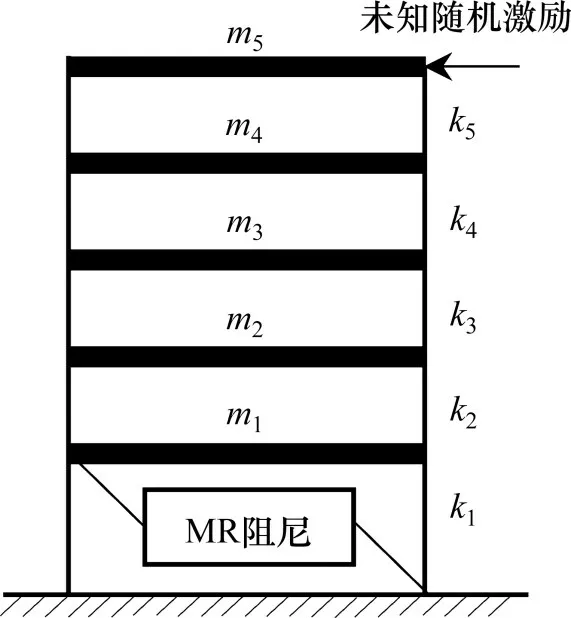
图5 装有MR阻尼的5层模型Fig.5 Five-floor numerical model with MR damper
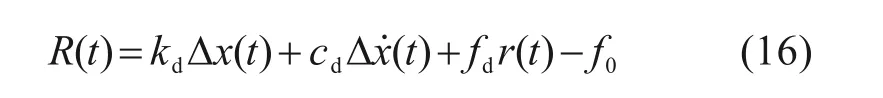
其中:kd为Dahl 模型刚度系数;cd为Dahl 模型黏滞阻尼系数;fd为可调库伦摩擦力;f0为初始力;Δx(t)和Δ(t)分别表示结构层间位移和层间速度,r(t)表示滞回位移,由以下微分方程确定:
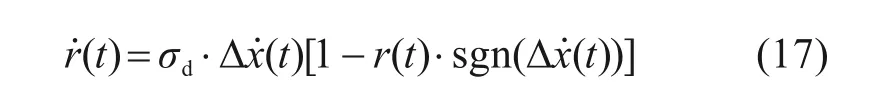
其中:参数σd用于控制滞回曲线形状。
系统参数取值如下:各层的质量和刚度分别为200 kg 和350 kN/m,瑞利阻尼系数分别为α1=0.53,α2=1.29×10-3,Dahl 模型参数为kd=35 N/m,cd=250 (N·s)/m,fd=200 N,σd=2 000 s/m,f0=0 N。假设外激励作用于结构顶层,对应的非线性响应采用4 阶龙格-库塔法计算,时间步长为0.001 s。取结构第1,3,4 和5 层的加速度响应作为观测值,并考虑3%的噪声影响。
待识别的参数包括Dahl非线性模型的4个参数(kd,cd,fd和σd),以及剪切型结构的刚度和阻尼系数,系统噪声协方差矩阵R=I,观测噪声协方差矩阵Q=10-4I,初始值均取对应真实值的50%。利用本文提出的方法,以上参数的识别结果如表3所示。可以看出,各参数的识别值与真实值均较为接近。图6 给出了部分参数的收敛情况,很明显,识别值能稳定收敛于真实值附近。图7(a)给出了未知外激励的识别情况,可以看出,识别值与真实值吻合得较好。此外,基于以上识别的Dahl 模型参数,图7(b)进一步给出了该模型的非线性恢复力,不难发现,恢复力的估计值与真实值比较接近。
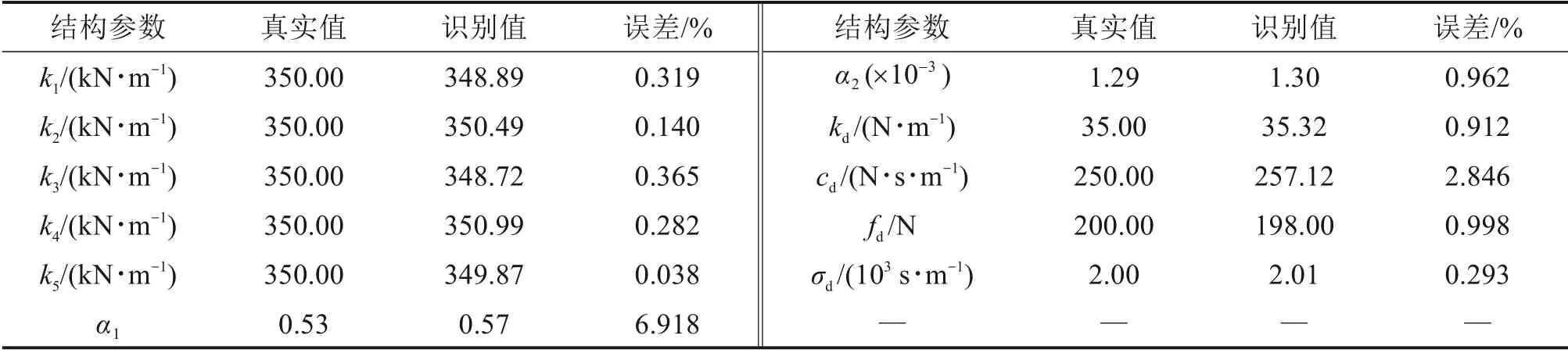
表3 未知激励下Dahl模型参数识别结果Table 3 Ⅰdentification of the Dahl model under unknown excitation
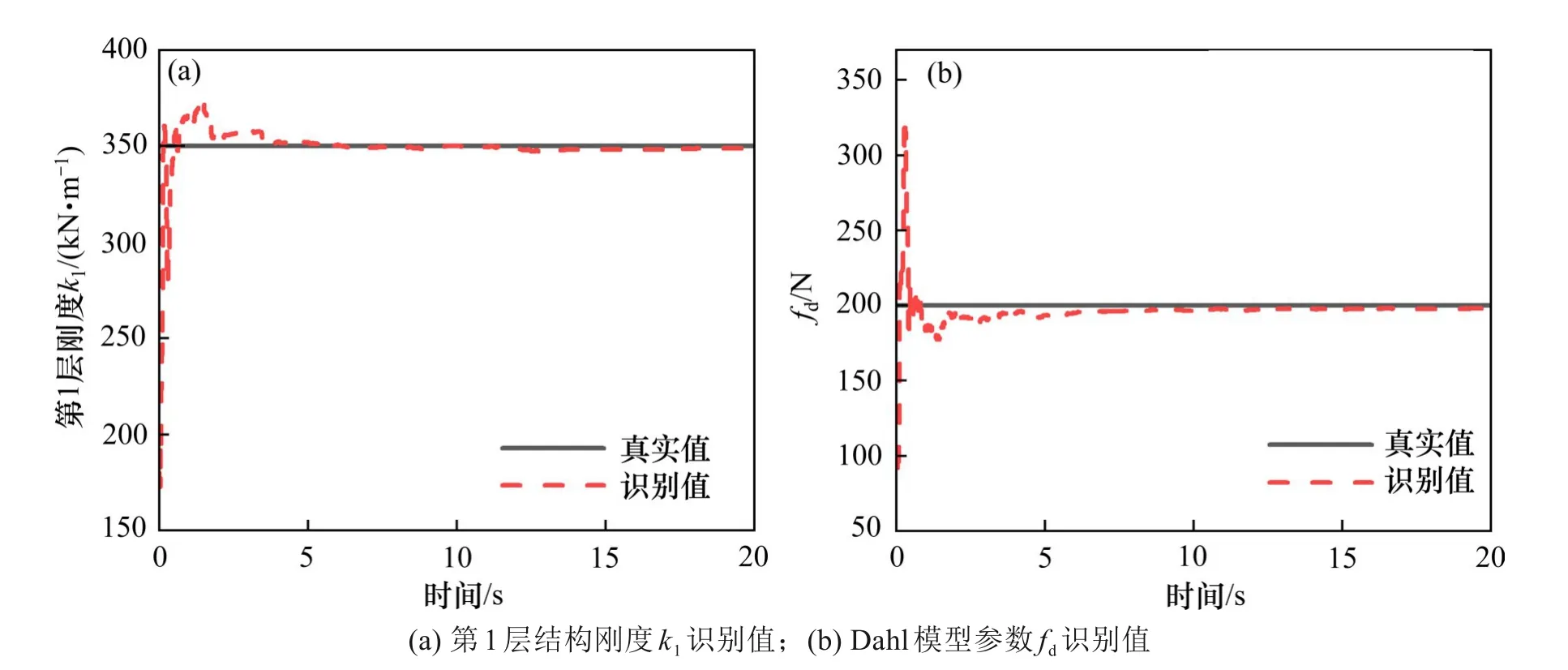
图6 Dahl模型部分参数识别结果Fig.6 Part of identified result of the Dahl model
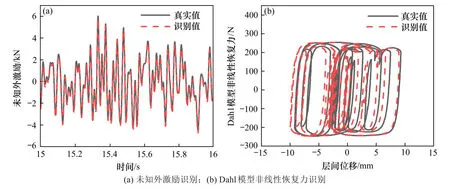
图7 未知外激励和非线性恢复力的识别结果Fig.7 Ⅰdentification of unknown excitation and nonlinear restoring force
3 结论
1) 提出了一种基于EKF 的结构参数和未知荷载的识别方法,利用初等行变换矩阵与观测方程组构成的矩阵方程进行消元,从而使观测方程中不含未知外激励,并利用改进后观测方程和系统状态方程对结构状态和外激励进行识别。
2) 以数值算例为主,通过剪切型结构和桁架结构验证了本方法对于线性系统识别的可行性,此外,通过装有Dahl 模型的五层框架数值算例进一步验证了本文方法对于非线性系统识别的有效性;相关的实验研究将在后续的研究工作中开展,以验证实际结构的可行性。
