Peck公式参数的几种取值方法研究

尹光明，傅鹤林，侯伟治，严石生

(1. 长沙轨道交通集团有限公司，湖南 长沙 410031；2. 中南大学 土木工程学院，湖南 长沙 410075)

在现有的Peck 公式的研究中，大多是基于对现有实测数据的总结统计，而后借助数值回归分析的手段选取经验取值。姚爱军等[1]基于对大量的工程实测数据的回归统计，得出了最大沉降值及沉降槽宽度的修正系数，将修正结果与实测值进行对比，结果表明两者有较好的吻合性。方恩权等[2]以在建隧道为工程依托，以Peck公式为理论基础，将插值法和最小二乘法引入信息系统，建立了信息系统模型用以预测隧道开挖下的地表沉降，能实现地表沉降的快速预测。朱才辉等[3]总结了关于地表最大沉降值的计算公式及其适用性，以实测资料为依据，总结讨论了高跨比、地层条件和施工方法等与Peck 公式参数之间的经验关系。吴昌胜等[4]基于对大量实测数据的研究分析，以Peck公式为研究基础，反求了不同盾构直径下的地层损失率，研究表明地层损失率和盾构直径有明显的分布关系。韩煊[5]在随机介质理论中引入了不均匀收敛的隧道变形模式；但是，采用回归分析的方法选取经验取值欠缺必要的理论支撑，结论的正确性有待进一步的探究。另外，不同工程的差异，简单地将现有实测数据所得结论适用于其他工程往往适用性不佳，导致预测不准。因此，本文基于Peck 公式，通过对公式结构的分析变形，提出了针对不同隧道工程下，沉降槽宽度和地层损失量取值获取的几种方法，以便提高Peck 公式在工程应用中的适用性和便利性。

1 沉降槽宽度i的取值分析

观察Peck公式的具体表达式，

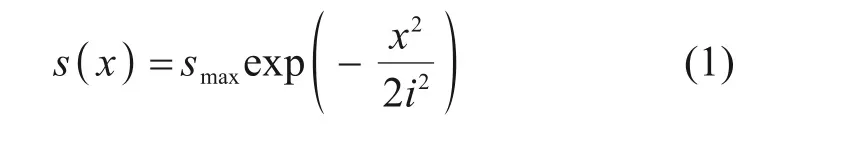
对式(1)做如式(2)的变形：

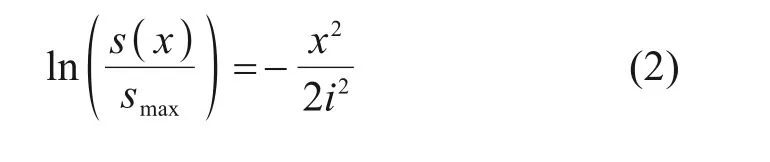
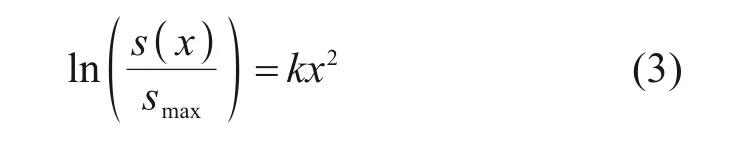
式中：s(x)为由地层损失引起的地表沉降，mm；x为到隧道轴线的距离，m；i为沉降槽宽度，即沉降曲线拐点到对称中心的距离，m；smax为隧道轴线正上方的地表处沉降值，m。

为了进一步验证在大埋深情况下沉降槽宽度i的取值情况，借助数值分析的方法，对不同工程概况进行模拟分析，以探明各影响因素对沉降槽宽度i的具体影响情况，根据实际工程和工程地质手册，不同土体的物理力学性质指标如表1所示[6]。

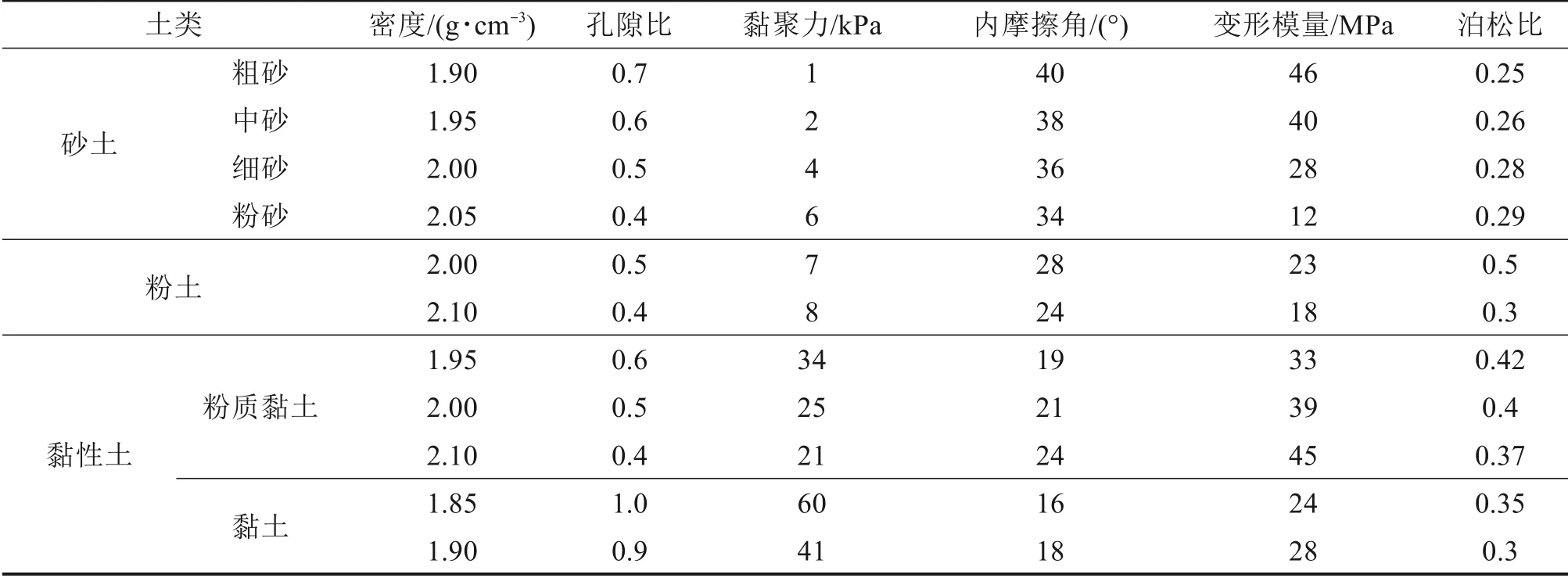
表1 土的平均物理力学性质指标Table 1 Average physical and mechanical properties of soil

采用岩土数值分析软件FLAC3D，建立模型，模型大小为100 m×60 m×30 m，模型上表面为自由面，其余表面约束其法向位移，土体采用Mohr-Coulomb 本构材料，根据表1 选取计算参数，其中变形模量换算成体积模量。分别考虑隧道开挖半径R和隧道埋深z0对沉降槽宽度i取值的影响，为了便于比较分析，采用控制变量的方式逐个研究分析各个因素的影响情况。

1.1 隧道埋深z0对沉降槽宽度i的影响分析

为探明隧道埋深z0对沉降槽宽度i的影响，在实际工程概况的基础上，建立埋深梯度变化数值模型，具体的模型隧道埋深z0参数设计如表2 所示。通过FLAC3D数值分析软件模拟不同的埋深z0开挖下，地表的沉降变形情况。

表2 模型隧道埋深z0参数设计Table 2 Design table of buried depth z0 parameters of model tunnel

根据式(3)算得沉降槽宽度i的具体值，并对其进行分析拟合，经FLAC3D计算得不同埋深下的沉降槽宽度i如表3所示。

根据表3 中的统计结果，若将隧道开挖半径R视为一常数，对于沉降槽宽度i可选用常用计算式拟合[7-12]：

以式(4)对表3中的统计结果进行拟合分析，得到图1 所示的拟合结果。从图1 可以看出，以式(4)的形式拟合沉降槽宽度i与隧道埋深z0的变化情况，有较好的拟合性，这说明沉降槽宽度i随隧道埋深z0的变化符合式(4)的描述。在后续类似工程中，针对更多实测数据的处理时，以式(4)寻求沉降槽宽度在某一埋深下的值是较为合理的。

表3 不同埋深下的沉降槽宽度iTable 3 Width i of settlement trough under different buried depth

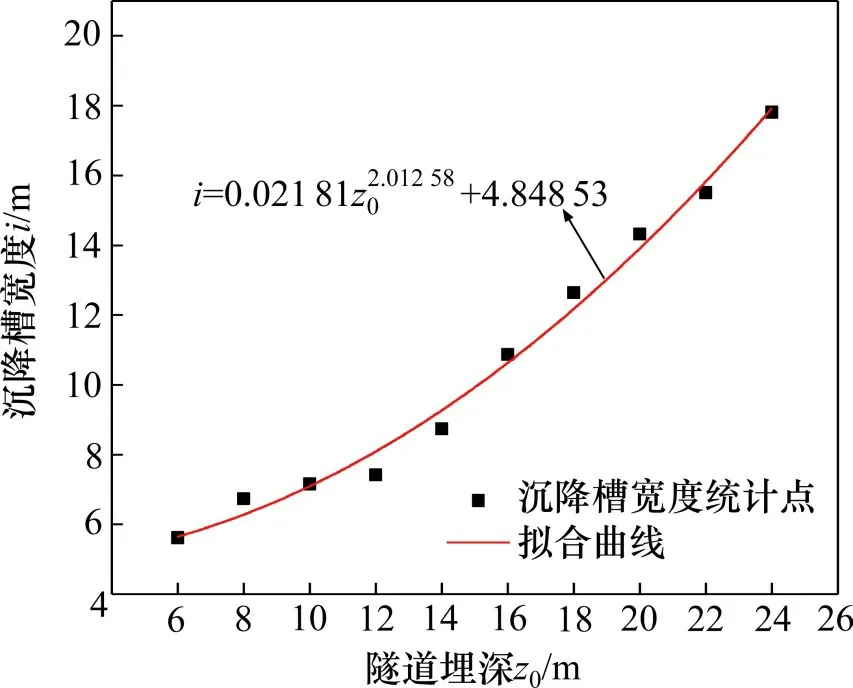
图1 沉降槽宽度随隧道埋深的变化及拟合情况Fig.1 Variation and fitting of settlement trough width with tunnel dept

1.2 隧道开挖半径R对沉降槽宽度i的影响分析

为探明隧道开挖半径R对沉降槽宽度i的影响，在实际工程概况的基础上，建立开挖半径梯度变化数值模型，具体的模型开挖半径R参数设计如表4 所示。通过FLAC3D数值分析软件模拟不同开挖半径R开挖下，地表的沉降变形情况，根据式(3)算得沉降槽宽度i的具体值，并对其进行分析拟合，经FLAC3D计算得不同开挖半径下的沉降槽宽度i如表5所示。

表4 模型开挖半径R参数设计Table 4 Model excavation radius R parameter design

根据表5 中的统计结果，对考虑开挖半径R影响的计算式进行拟合，具体结果如图2所示。

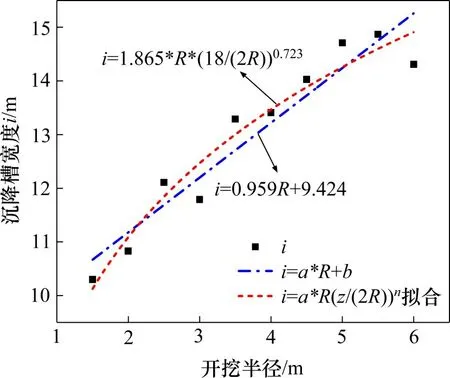
图2 i～R拟合关系Fig.2 i～R fitting relationship

表5 不同开挖半径下的沉降槽宽度iTable 5 Width i of settlement trough under different excavation radius

从拟合关系看，在埋深一定的情况下，开挖半径对于沉降槽宽度的影响呈现出正相关，即开挖半径R越大，沉降槽宽度i越大，并不能简单忽略开挖半径对沉降槽宽度i的影响，为了进一步研究开挖半径对沉降槽宽度的影响，取埋深/洞径比分别为1，2 和3，将不同埋深/洞径比下的沉降槽宽度统计如表6所示。

根据1.1 节拟合结果，分析不同埋深与开挖洞径比值情况下对应的沉降值宽度值，借助前述分析由拟合式计算得到的沉降槽宽度i值结果如表7所示。对比表6 和表7，将不同埋深/洞径比下的结果绘制成图3所示。

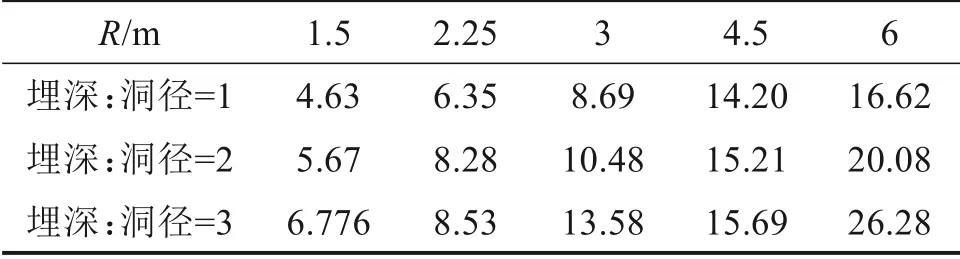
表6 不同埋深/洞径比下的沉降槽宽度i值情况Table 6 Width i of settlement tank under different buried depth/tunnel diameter ratio

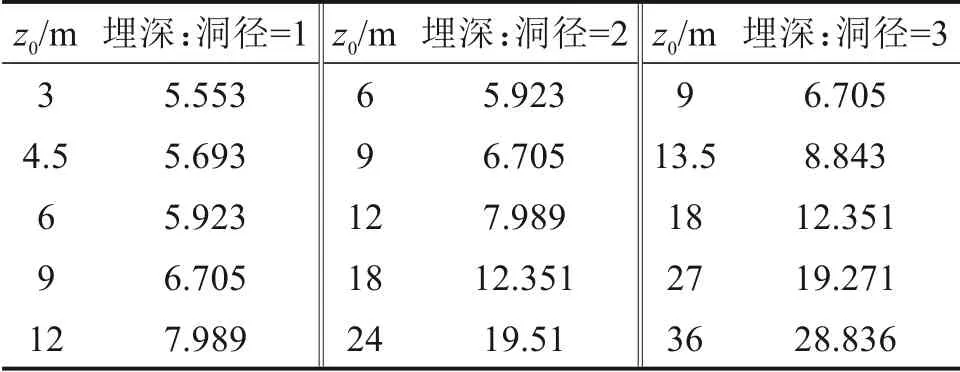
表7 拟合式计算的沉降槽宽度i值情况Table 7 Settlement trough width i calculated by fitting formula

从图3可以看出，在埋深/洞径比等于1时，数值计算结果与不视开挖半径为一常数的拟合计算结果偏差较大，但当埋深/洞径比为2和3时，沉降槽宽度的值具有相同的增长趋势，且偏差较小，这说明开挖半径的影响在埋深/洞径比大于等于2时可近似忽略，即当z0/2R≥2时，可不考虑开挖半径R对沉降槽宽度i的影响。

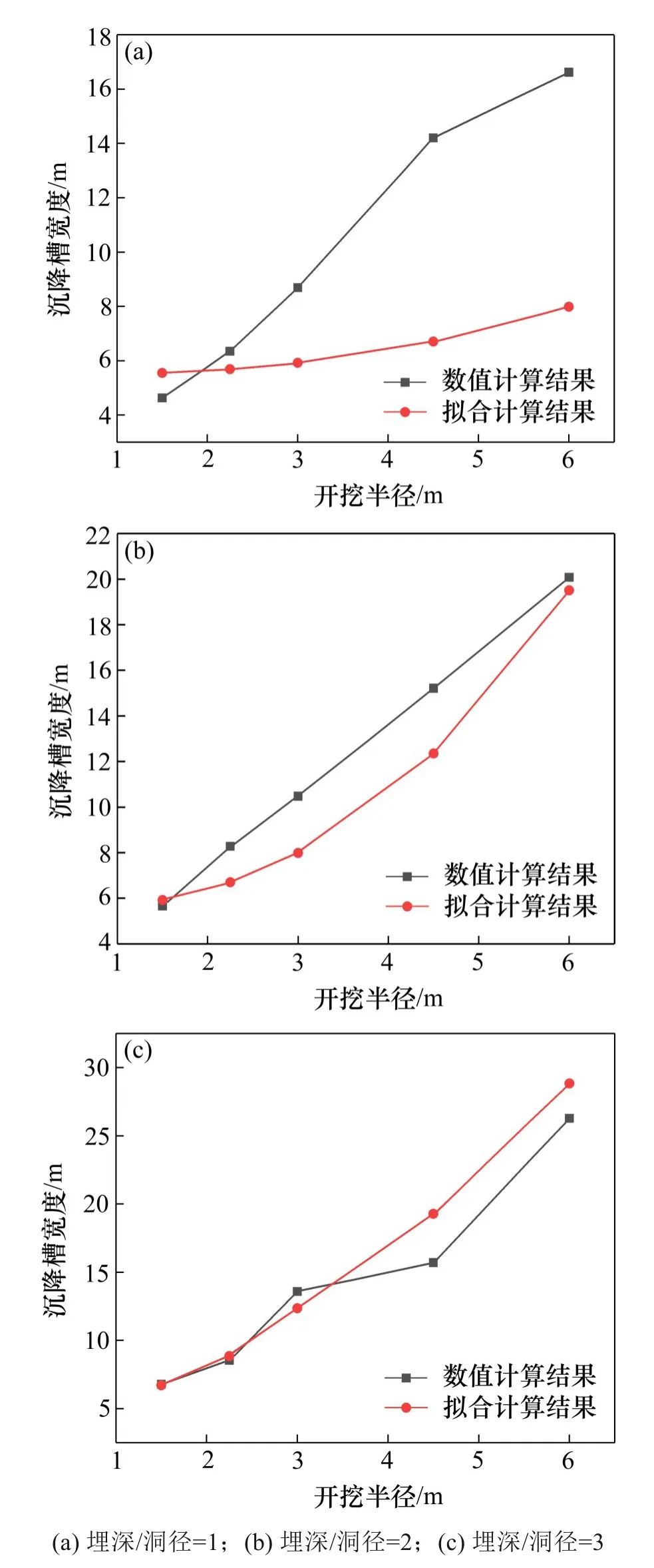
图3 不同埋深/洞径比下的沉降槽宽度值情况Fig.3 Width of settlement trough under different buried depth/tunnel diameter ratio

1.3 土体内摩擦角φ对沉降槽宽度i的影响分析

为探明隧道土体内摩擦角φ对沉降槽宽度i的影响，在实际工程概况的基础上，建立开挖半径梯度变化数值模型，具体的模型土体内摩擦角φ参数设计如表8所示。

表8 模型土体内摩擦角φ参数设计Table 8 Parameter design of internal friction angle φ of model soil

通过FLAC3D数值分析软件模拟不同土体内摩擦角φ开挖下，地表的沉降变形情况，根据式(3)算得沉降槽宽度i的具体值，

并对其进行分析拟合，经FLAC3D计算得不同内摩擦角下的沉降槽宽度i如表9所示。

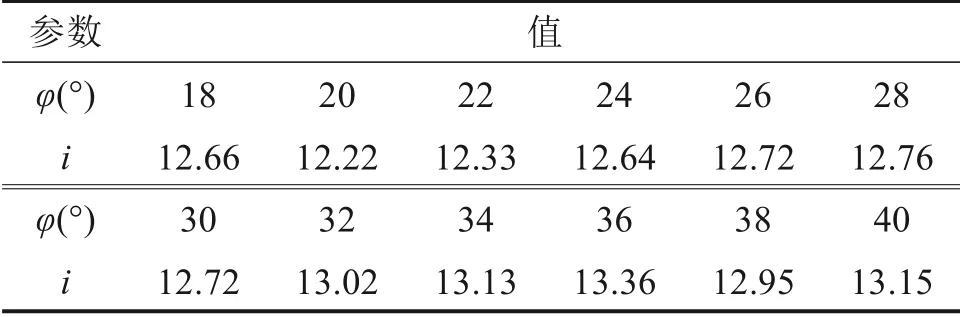
表9 不同内摩擦角下的沉降槽宽度iTable 9 Width i of settlement trough under different internal friction angles

根据表9中的统计结果，参考文献[7]中对于内摩擦角的考虑，认为，将表9的结果处理得到图4所示的结果。

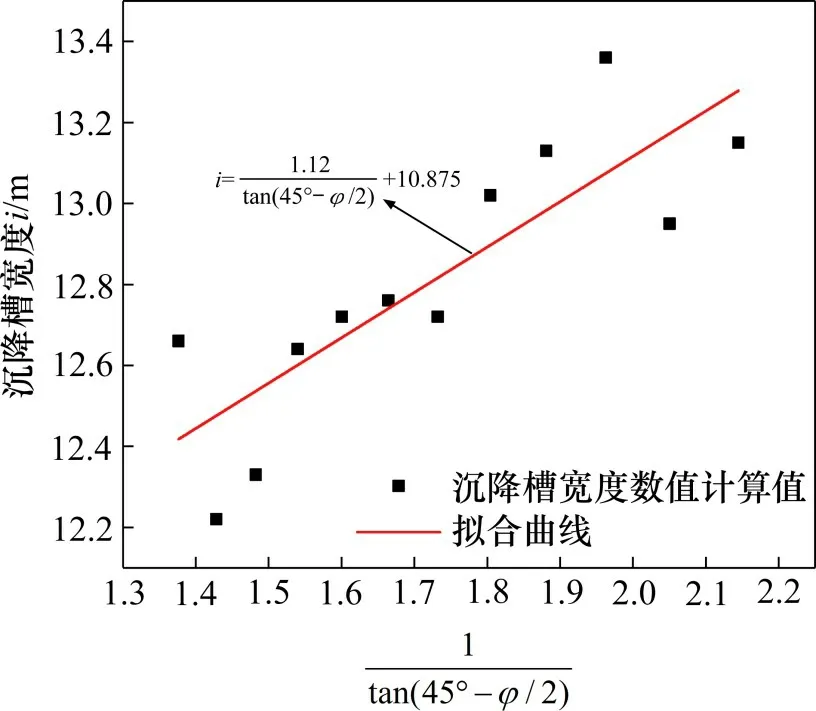
图4 i随的变化情况Fig.4 i changes with

从图4可以看出，在埋深一定的情况下，沉降槽宽度i随的增大而增大，i值在线性拟合曲线的上下小范围内波动，这在一定程度上说明了线性变化的正确性，从工程的角度而言，对于隧道的开挖，因埋深的确定性，为控制开挖的影响范围，可通过注浆或者施加预应力锚杆等工程措施改变土层的内摩擦角φ以控制地表的变形范围在某一限制值。

2 地层损失量Vi的计算分析

2.1 基于沉降槽宽度已知情况下的地层损失量计算讨论

观察Peck公式的计算表达式，

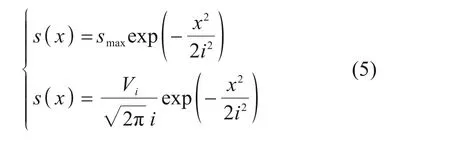
若已知沉降槽宽度i和地表最大沉降值smax，则根据式(5)，地层损失量Vi可由式(6)算得。

或在已知沉降槽宽度i的情况下，可通过地表的任一沉降点求得地层损失量Vi。

2.2 基于无实测数据情况下的地层损失量计算讨论

隧道在开挖后，因施工工法的影响，常产生超挖或衬砌间隙等，土体在重力和初始地应力的作用下，会表现出向空隙处的移动填充，产生应力重分布的现象，由于土的颗粒性和连续性，土层的移动会不断向上传导，直至传导至地表临空面变现出地表的沉降变形，即隧道开挖引起的地表变形可归结为：地层损失、围岩及衬砌结构产生应变—地层发生位移—地表变形。

现假设在距地表H埋深处，有一开挖半径为R的圆形隧道，隧道在土体开挖完成后，围岩应力状态发生重分布，应力再次达到平衡状态，隧道周边土体发生移动变形，表现为指向隧道中心处的径向收敛，最终围岩的移动变形达到稳定，此时，假设隧道断面产生均匀的径向收敛ΔR，如图5所示。

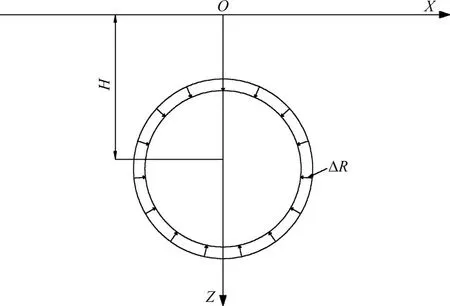
图5 隧道开挖示意图Fig.5 Schematic diagram of tunnel excavation

事实上，地层开挖下的地层扰动是极为复杂的，即使将隧道的收敛简化为均匀的径向收敛情况，通常也较难直接获取收敛值ΔR，为此，常用的用以确定地表变形参数的取值方法主要有：1) 利用现场实测资料绘制地表变形曲线反求基本参数的图解法；2) 通过与类似工况类似地质条件对比分析，由已有资料选取适合的地表变形参数的工程类比法。但上述图解法和工程类比法受制图精度和工程地质条件的限制，所确定的基本参数一般误差较大[13-15]。

在隧道均匀收缩的情况下，隧道断面径向收敛ΔR与Peck公式中Vl具有相同的计算意义，均是衡量隧道开挖后断面的变形值，基于此建立断面收缩半径ΔR与地层损失量Vi之间的算术关系式并汇总于表10。

表10 隧道径向收敛值ΔR与地层损失量Vi之间的换算式Table 10 Conversion formula between tunnel radial convergence value ΔR and formation loss Vi

3 基于多数据点的Peck 公式参数取值计算

上述关于地表沉降槽宽度及地层损失量的讨论研究给出了基于2 个数据点及无实测数据时，Peck 公式地表沉降参数的计算取值模型，当现场实测数据足够多时，因误差总是围绕真实值上下波动，足够多的实测数据可减小误差的影响。基于此，根据已有的数据点对其进行Peck 公式拟合，即可求得对应数据点下的Peck 公式计算参数取值，具体的计算结果如图6所示。

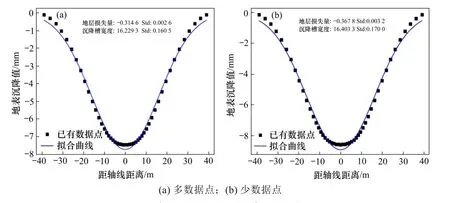
图6 多数据点与少数据点情况下的对比Fig.6 Comparison of multiple data points and a few sites

对于实际的监控量测数据点，当在较少数据点的情况下，拟合结果可能会出现较大的标准差，即拟合获得的参数可能存在一定的偏差，如图7所示。通过数值模拟对拟合所获得的沉降槽宽度进行验证，结果表明拟合所得沉降槽宽度与数值模拟所得的误差在10%以内，认为拟合得到的沉降槽宽度是可靠的。

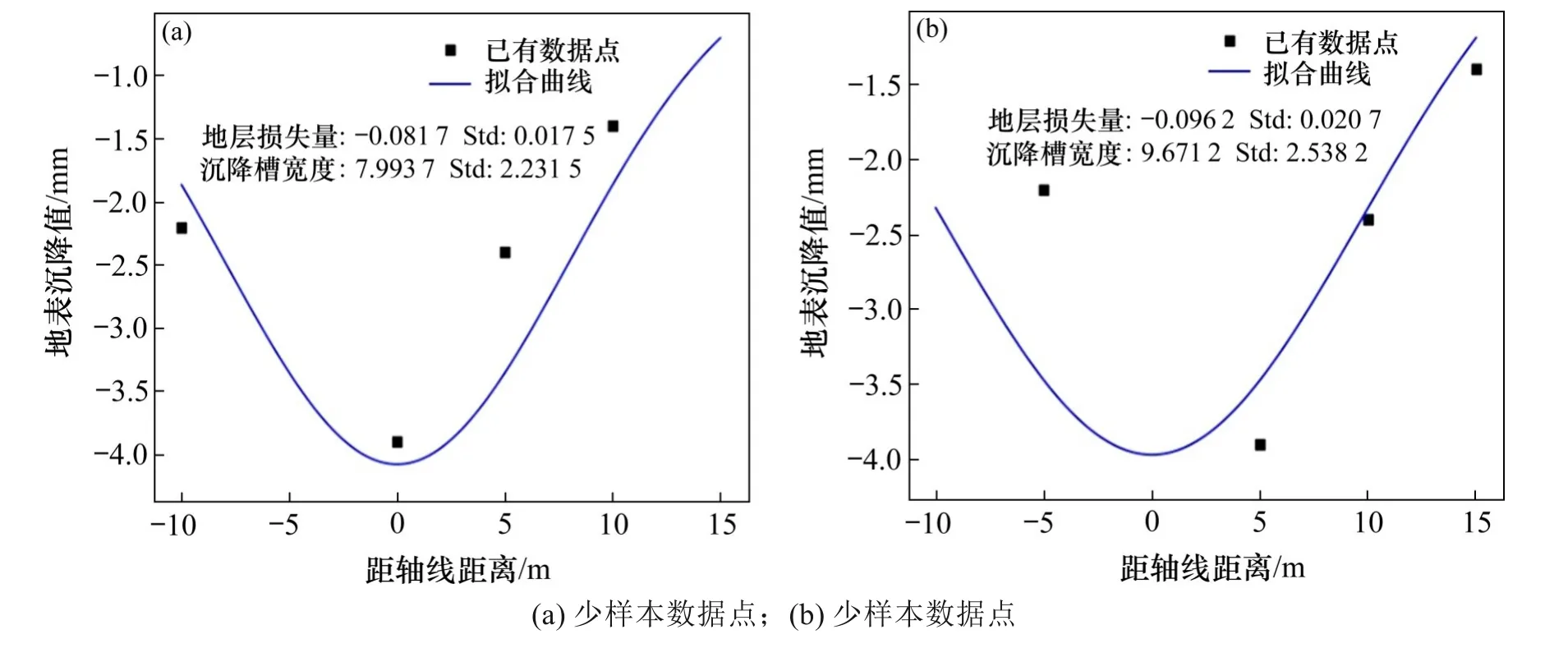
图7 数据点较少情况下的拟合情况Fig.7 Fitting situation under the condition of few data points

从图7 可以看出，在较少的数据点的情况下，其沉降槽的拟合结果出现较大的标准差，这说明此方法的应用前提是需要基于已有较大数据量的情况下，才能得到较好的拟合结果，对于实际工程的应用，可通过建立施工数据库，将此方法接入数据库，基于数据库中大量数据的前提下，实现地表沉降的动态预测。

4 结论

1) 通过对Peck 公式结构的变形，建立了在数据样本点较少时，沉降槽宽度的分析计算模型，并基于此讨论分析了沉降槽宽度与隧道埋深、隧道开挖半径之间的关系，通过回归分析的手段给出了各影响参数在不同取值时关于沉降槽宽度的建议取值，通过不同宽高比的对比研究，分析了隧道埋深与隧道开挖半径比值对沉降槽宽度的影响情况。

2) 讨论了基于沉降槽宽度已知情况下地层损失量的求解方法，分析了地层损失量Vi与断面收缩值ΔR间的关系，并给出了对应的换算关系式。

3) 借助编程计算工具，对已有地表沉降数据点样本进行Peck 公式拟合，建立了基于多数据情况下Peck 公式参数取值的获取方法，并分析了在多样本数据点和少样本数据点下的拟合情况，认为拟合获取参数的方法需在已有数据样本点较大的情况下才能获得较好的拟合结果。