超250 m级高塔铁路斜拉桥减隔震设计参数影响分析

董俊 ，曾永平，张金，黄树强，宋晓东

(1. 四川建筑职业技术学院，四川 德阳 618000；2. 中铁二院工程集团有限责任公司，四川 成都 610031)

斜拉桥以其跨越能力大、复杂地形适应性强等优点，过去近半个世纪内在世界各国得到了迅速的发展，并且其跨度在不断的递增。截止2021年世界各国共设计建造了550多座斜拉桥，大部分为公路斜拉桥[1-2]，铁路斜拉桥占比较小。目前国内已建成通车的铁路专用斜拉桥屈指可数，如红水河大桥[3]、韩家沱长江大桥[4]、北江特大桥[5]、思贤窖特大桥[6]、安庆长江铁路大桥[7]、甬江特大桥[8]和桂平郁江特大桥[9]，这其中公铁两用斜拉桥相对较多，但大部分都是在最近十多年设计建造的[10]。为了跨越地形复杂多变的西南艰险地区，铁路斜拉桥正逐渐被采用，但目前我国铁路斜拉桥中对于塔高超过250 m 级的大跨度铁路斜拉桥尚属于空白[11]。由于列车活载远大于公路活载值，使得超高塔的抗震、抗风等问题更加突出，因此这类超高塔大跨铁路斜拉桥设计将面临一系列的技术壁垒。目前很多学者对斜拉桥抗震及减震相关领域开展了研究，韩振峰等[12]针对千米级大跨度斜拉桥，研究大桥几何非线性对桥梁抗震性能的影响，研究了适用于大桥的减隔震体系。邱景雷等[13]针对200 m级公路高塔斜拉桥开展了大桥动力特性分析，对黏滞阻尼器条件下大桥地震性能及减震效果进行了研究。黄永福等[14]以100 m 级高塔大跨公路斜拉桥为研究背景，开展了4种抗震体系下大桥地震响应分析研究，并对约束参数进行了敏感性分析，提出了合理的设计参数。上述研究成果主要针对公路斜拉桥，对于铁路斜拉桥研究相对较少，而像250 m 级高塔铁路斜拉桥更是未见报道。此外西南山区地震带分布密集，抗震问题已成为超高塔铁路斜拉桥设计的突出问题。因此本文将以正在开展设计的某铁路超高塔大跨斜拉桥为研究背景，开展这类桥梁的合理减隔震设计参数分析研究。

1 工程案例

1.1 工程概况

西南山区某铁路关键控制性工程拟采用(70+208+500+208+70)m 双线铁路钢桁梁斜拉桥。尽管在选线时尽量压低了桥位处的线路标高，但该桥面以下塔高(下塔柱)仍然高达146 m。且根据最新的勘察设计资料，为了减少两端隧道的施工风险与展线的困难，线路还将抬高40 m，桥面以下将达到186 m，整个塔高将高达287 m。大桥集“180 m 级高墩、超250 m 级高塔、500 m 级跨度”组合于一体。

大桥孔跨样式为(40+72+40) m 连续梁+(56+222+500+222+56) m 斜 拉 钢 桁 斜 拉 桥+1×24 简 支梁，桥长1 244.45 m(主桥布置图见图1)，结构主梁采用钢桁架梁，桁高14.5 m，桁宽22 m，上弦杆采用120×110 cm 箱形截面，下弦杆采用148×115 cm 箱形截面，中竖杆和中腹杆采用110×80×5 cm 工字钢，桥塔采用A 型桥塔，截面形式为空心梯形截面，其混凝土标号采用C55，1 号边墩墩高52 m，2号辅助墩墩高62.03 m，5号辅助墩墩高35.13 m，左侧和右侧主塔高度分别为251 m 和287 m，大桥采用半漂浮体系，塔梁横向设置抗风支座，在两桥塔、墩梁处设置黏滞阻尼器，1 号和4 号边墩采用TJGZ-Q6000 型球型钢支座、2 号和3号辅助墩采用TJGZ-Q18000 型球型钢支座，两桥塔采用TJGZ-Q50000 型球型钢支座。桥址区地震动峰值加速度为0.10g，场地特征周期为0.35 s。图2和图3分别给出了主塔、主梁的断面图。

图1 斜拉桥主桥总体布置图Fig.1 General layout of cable-stayed bridge

图2 桥塔和主梁断面Fig.2 Diagram of bridge pylons and girders

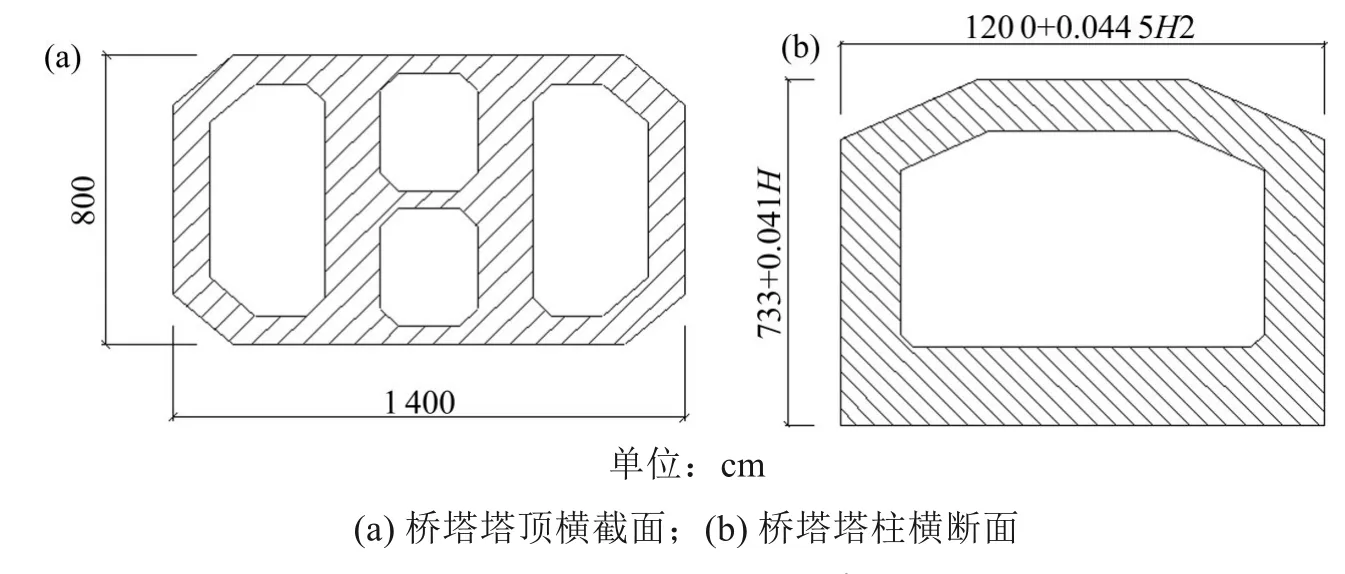
图3 桥塔断面构造示意图Fig.3 Schematic diagram of bridge tower section structure

1.2 有限元模拟

采用Midas/civil建立了全桥模型，钢桁梁采用梁单元模拟，斜拉索采用只受拉的桁架单元模拟[15]，桥墩和桩基础采用梁单元模拟，因采用半漂浮体系，故支座采用双折线支座本构模型进行模拟[16]，黏滞阻尼器采用Maxwell 模型模拟，桩土相互作用参考文献[17]求解各桩基的水平弹簧刚度，参考规范[4]考虑二期恒载和列车荷载作用。

1.3 地震动输入

依据桥址处的地震烈度信息等参数，按照《铁路工程抗震设计规范》得到规范反应谱，采用人工合成的方法生成了多遇、设计、罕遇地震波各3 条，罕遇wave1 地震动时程曲线如图5，其对应的反应谱曲线见图6。

图4 全桥有限元模型示意图Fig.4 Schematic diagram of the finite element model of the whole bridge

图5 罕遇人工地震波1时程Fig.5 Rare earthquake wave 1 time history

图6 罕遇人工地震波1的反应谱与规范谱对比Fig.6 Comparison of response spectrum and code response spectrum of rare earthquake wave 1

1.4 动力特性分析

参考文献[13]和[19]用多重Ritz 向量法计算大桥动力特性，使得参与的振形阶数质量占总体质量的比例超过90%。动力分析过程中，塔梁纵向弹性约束刚度取7.5×104kN/m，塔梁横向约束刚度取1×106kN/m。大桥特征周期及振型特征见表1。前2阶振型图见图7，由表1分析可知，大桥1阶周期为5.32 s，为长周期柔性结构，1 阶振型为主梁纵桥，与大桥采用的支撑体系密切相关。由于桥塔高度超过250 m，桥塔自身刚度较小，在前3 阶振型中存在桥塔横弯的振型，在减隔震设计时应当给予关注。

图7 大桥振型布置图Fig.7 Vibration mode layout of the bridge

表1 大桥动力特性分析Table 1 Dynamic characteristics analysis table of bridge

2 塔梁纵向弹性连接刚度对大桥动力特性和地震响应影响分析

2.1 塔梁纵向弹性连接刚度对大桥动力特性的影响

为分析塔梁纵向弹性约束刚度对大桥动力特性影响，取弹性约束刚度值分别为0.0，1.0×104，5.0×104，1.0×105，1.0×106，1.0×107，1.0×109kN/m，进行了一系列动力特性分析，纵向弹性刚度对大桥主要振型的影响结果列于表2。

由表2分析可知：塔、梁间纵向连接弹性刚度变化对超高塔铁路斜拉桥纵飘特征周期影响显著，对主梁反对称竖弯有一定的影响，对主梁正对称竖弯影响小。随着塔、梁间纵桥向弹性约束刚度的加大，主梁纵飘、主梁对称竖弯振型、主梁反对称竖弯振型的自振频率均逐渐增多，周期均逐渐减小。弹性约束刚度K取0～1×106kN/m 范围内对结构的纵飘振型影响较大，超过1.0×106kN/m后，影响不明显。同时随着塔、梁间顺桥向弹性约束刚度的加大，纵飘振型出现的阶次逐渐后移。

表2 塔梁纵向弹性约束刚度对大桥振型的影响分析Table 2 Table of influence of longitudinal elastic constraint stiffness of pylon and beam on vibration mode of bridge

2.2 塔梁纵向弹性连接刚度对超高塔地震响应的影响

为分析塔梁纵向弹性约束刚度对超高塔地震响应的影响，取纵向弹性约束刚度K分别为0.0，1.0×104， 5.0×104， 1.0×105， 1.0×106， 1.0×107和1.0×109kN/m，进行全桥时程反应分析。时程分析时输入的地震动为1.3 节按规范反应谱拟合的3 条罕遇人工地震波。由于塔、梁间的顺桥向弹性连接的刚度对主塔的顺桥向地震反应影响较大，对横桥向的反应影响较小，因此本节主要研究了塔、梁间的弹性连接刚度对主塔内力及位移的影响。选取左、右桥塔各5个关键截面为分析对象，按规范取3 条波最大值作为分析数据。图9 给出了各关键截面地震响应与弹性刚度的变化关系。

图8 桥塔关键截面编号示意图Fig.8 Schematic diagram of key section number of bridge pylon

由图9分析可知：

图9 纵向弹性刚度与桥塔内力及变形关系曲线Fig.9 Relation curves of longitudinal elastic stiffness to internal force and deformation of pylon

1)当弹性连接刚度增大时，塔顶5-5 截面的弯矩、剪力和上塔柱4-4 截面弯矩总体变化趋势为先减小后增大。下塔柱3-3 和2-2 截面的弯矩、剪力随刚度的增加而逐渐递增，最后趋于稳定。

2) 当纵向连接刚度增大时，主塔塔顶及主梁梁端位移先增大后减小，最后趋于平稳，当弹性约束刚度在1.0×106kN/m以下时，结构的位移曲线变化较陡，当大于1.0×106kN/m时，结构的位移曲线变化较为平缓。

3) 塔、梁间若采用弹性约束，刚度取值为50 000 kN/m左右时，结构抗震性能较好。

3 超高塔铁路斜拉桥减隔震参数优化分析

根据超高塔铁路斜桥的结构特点，通过设计过程中前期的试算发现，仅在桥塔处设置黏滞阻尼器很难满足高塔铁路斜拉桥抗震需求，需在边墩、辅助墩也设置黏滞阻尼器，具体布置方式为：每个塔梁处设置2组黏滞阻尼器，各墩梁处设置一组黏滞阻尼器，全桥共设8组黏滞阻尼器。为研究阻尼器的合理参数，以3 条罕遇(100 a 超越概率4%)人工地震波为输入地震波，基于非线性时程分析，研究阻尼指数α和阻尼系数C变化时对应大桥关键部位地震响应的影响规律。

黏滞阻尼器参数工况具体设置如表3所示。

表3 黏滞阻尼器参数优化工况Table 3 Viscous damper parameter optimization condition

3.1 设计参数对主梁及支座位移影响分析

图10 给出了各阻尼指数α下桥塔和桥塔支座位移随阻尼系数c的变化规律。

图10 桥塔支座和梁端位移随阻尼器参数变化曲线Fig.10 Curves of displacement of support and beam end with damper parameters

从图中可以看出，各阻尼指数α下，左桥塔和右桥台支座位移变化总体趋势一致，支座位移均随着阻尼系数C的增大而减小，且阻尼指数α取值越大，支座位移值越小。总体来看，当阻尼系数C取值大于10 000 (kN·s)/m 后，支座位移曲线变化趋于平缓。阻尼指数取值大于0.4 时，位移响应值近 似 趋 于 平 缓。 具 体 的， 当α=0.5，C=15 000 (kN·s)/m 时，桥台处主梁梁端位移峰值为0.505 m，比较无阻尼器情况下的梁端位移峰值1.10 m，位移减少率为55.1%，位移减小效果显著。为了控制主梁支座位移和梁端位移，同时考虑阻尼参数设置的实际限位效果，推荐阻尼系数C取8 000～12 000 (kN·s)/m，阻尼指数α取0.3～0.4，此时支座位移可控制在0.55 m，梁端位移可控制在0.6 m内。

3.2 设计参数对桥塔关键截面内力影响分析

图11 给出了右侧桥塔1-1～5-5 各控制截面弯矩和剪力随阻尼器参数变化的趋势曲线。

由图11 分析可知，各阻尼指数α条件下，右塔1-1，2-2，3-3 控制截面弯矩和剪力响应峰值其总体趋势均随C值的增大而增大，而后逐渐趋于平稳。但对于不同桥塔截面位置，设置阻尼器后的弯矩剪力响应峰值较无阻尼器情况下的响应峰值大小关系却不尽相同。右塔4-4 和5-5 控制截面弯矩响应随C值的增大而减小，而剪力则是随C值的增大而增大。4-4 和5-5 2 个控制截面为上塔柱截面，由于黏滞阻尼器有效的减小了主梁的纵向位移，进而减小了拉索传递给上塔柱的内力，并且黏滞阻尼器本身会耗散掉一部分地震输入的能量。

图11 右侧桥塔关键截面内力随阻尼器参数变化曲线Fig.11 Curves of the internal force of the key section of the right pylon with the parameters of the damper

此外对于下塔柱各关键截面内力计算结果可知，随着阻尼指数α的逐渐增大，桥塔各关键截面的弯矩和剪力值也越来越小，减震效果也在提高，左侧桥塔的结果与右侧桥塔结果规律类似，这里不再详述。综合考虑右塔各控制截面内力与阻尼器参数的关系，使各桥塔关键截面承受的地震力较小，同时控制支座和梁端位移，推荐阻尼系数C取值小于10 000 (kN·s)/m，阻尼指数α 取值为0.4～0.5。

3.3 设计参数对各桥墩墩底内力影响分析

图12 给出了边墩、辅助墩墩底截面弯矩和剪力随阻尼器参数变化的趋势曲线。

从图12 分析可知：各阻尼指数α下，1 号边墩墩底截面弯矩、剪力地震响应峰值随阻尼系数C的增大而减小，2 号辅助墩墩底截面弯矩、剪力地震响应峰值随C值的增大先增大后减小，逐渐趋于平稳，3 号辅助墩墩底截面弯矩剪力响应峰值随C值的增大而增大，三者变化规律并不同步。但设置阻尼器后，3 个桥墩墩底截面响应均大于无阻尼器情况，这表明对于桥墩底部截面来说，主梁结构通过纵向黏滞阻尼器传递的外力使得其响应明显增大，且阻尼指数α取值越小，内力增大效果越明显。综合考虑各个桥墩墩底内力与阻尼参数的关系，使各桥墩墩底内力相对合理，推荐阻尼器参数设置为：桥墩阻尼器的阻尼系数C取值为6 000～10 000(kN·s)/m，阻尼指数ξ取值为0.4～0.5。

图12 各边墩、辅助墩墩底内力随阻尼器参数变化曲线Fig.12 internal forces at the bottom of each pier and auxiliary pier vary with the parameters of the damper

3.4 设计参数对阻尼力影响分析

图13 给出了阻尼力随阻尼器参数变化的趋势曲线。

从图13分析，除1号边墩与2号辅助墩对应的阻尼器外，相同阻尼指数α条件下，其余6 个阻尼器的阻尼力响应峰值随阻尼系数C的增大而显著增大。而1 号墩阻尼器的阻尼力随着C值的增大呈现先增大后减小，2 号墩阻尼器的阻尼力随着C值的增大呈递减趋势，主要是由于大桥左右不对称，且1 号边墩、2 号辅助墩墩高均大于5 号辅助墩，相对较柔，随着C值的增大而阻尼力在减小。

图13 各阻尼器阻尼力随阻尼器参数变化曲线Fig.13 Variation curves of the damping force of each damper with the parameters of the damper

综上所述，通过分析阻尼器参数对超高墩大跨斜拉桥桥墩内力、桥塔内力、支座位移、梁端位移等的影响规律，综合考虑大桥各关键部位的地震响应情况，兼顾工程经济性要素，最终推荐阻尼器参数设置为：阻尼系数C取8 000～10 000(kN·s)/m，阻尼指数α取值为0.4～0.5。

大桥具体的设计参数见表4。

表4 算例桥合理黏滞阻尼器设计参数Table 4 Reasonable viscous damper design parameters of bridge

4 大桥抗震性能评估

因大桥属于超高墩塔复杂桥梁结构，且跨度很大，技术复杂且维修困难，在采用减隔震措施后，依据规范[18]相关规定确定了大桥在地震水平Ⅰ，Ⅱ和Ⅲ水准下，大桥都应处于基本弹性状态的设计原则。根据桥塔和桥墩配筋图，建立相应的纤维模型，利用Xtract软件进行截面M-ϕ关系数值分析，得到了各桥塔、桥墩控制截面的承载能力值(见表5)。

表5 各控制截面弯矩曲率分析结果Table 5 Table of bending moment and curvature analysis results of each control section

采用本文第3节得到的大桥黏滞阻尼器合理设计参数，根据规范[18]对各关键截面进行抗震性能验算，由于篇幅有限本文仅给出罕遇地震作用下的验算结果，表6给出了桥塔、桥墩关键截面抗震验算结果。表7给出了支座在地震作用下横向剪力需求和纵向支座位移值。

表6 罕遇地震作用下桥塔、桥墩关键截面抗震验算结果Table 6 Seismic checking results of key section of bridge under rare earthquake

续表6

表7 大桥支座地震响应Table 7 Seismic response index of bridge bearing

由表4分析可知，在罕遇地震作用下，各桥墩墩底截面受力均处于弹性范围，满足规范要求。在罕遇地震作用下，桥塔上塔柱5-5 截面需求弯矩大于首次屈服弯矩，进入了弹塑性阶段，但其小于等效屈服弯矩，处于基本弹性状态，总体来说桥塔各控制截面受力均处于基本弹性范围，满足规范要求。

5 结论

1) 当塔、梁间弹性连接刚度增大时，超高桥塔各截面内力的变化规律各不相同，需要综合考虑各桥塔的受力情况，综合比选确定合理连接刚度；

2) 当塔、梁间弹性连接刚度增大时，塔顶及梁端位移总体上呈先增大后减小而后趋于平稳的趋势，当弹性约束刚度在1.0×106kN/m以下时，结构的位移曲线变化较陡，当大于1.0×106kN/m 时，结构的位移曲线变化较为平缓。

3) 对于超高墩大跨铁路斜拉桥，在塔梁和各桥墩处设置纵向黏滞阻尼器后，大桥梁端位移有明显的降幅，位移减震效果良好；对于超高桥塔而言，设置黏滞阻尼器后，桥塔上塔柱截面内力会明显降低，而下塔柱截面内力部分会增大；而边墩、辅助墩设置黏滞阻尼器后桥墩内力会增大，但能明显改善超高塔地震力分布情况，减小梁端位移，可以通过增加配筋和改变桥墩结构形式来提高其自身抗震性能；对于超高塔铁路斜拉桥而言，在桥塔、各桥墩设置黏滞阻尼器是必要的。

4) 通过分析阻尼器参数对“250 m 级超高塔、500 m 级跨度”铁路斜拉桥桥墩内力、桥塔内力、支座位移、梁端位移等的影响规律，综合考虑大桥各关键部位的地震响应情况，兼顾工程造价等要素，最终推荐大桥塔梁处设置2 组黏滞阻尼器，各墩梁处设置1 组黏滞阻尼器，单组阻尼器参数为：C取8 000～10 000 (kN·s)/m，α取0.4～0.5，可为今后类似工程提供参考依据。

5) 本文研究也存在一些不足，如在分析过程中，黏滞阻尼器在桥塔、辅助墩、边墩的具体参数值保持一致，并没有研究桥塔与桥墩取不同阻尼器参数时的大桥受力和变形情况，在今后的研究过程中，将进一步深入研究。