考虑地震动水力的跨海斜拉桥减震控制研究
2022-08-29雷虎军孙昱坤
雷虎军,孙昱坤
(1. 福建工程学院 土木工程学院,福建 福州 350118;2. 福建省土木工程新技术与信息化重点实验室,福建 福州 350118)
随着我国交通路网的进一步加密,跨海和跨水库等深水大跨桥梁不断涌现,采用高承台群桩基础的斜拉桥凭借其跨越能力强、造型优美,已成为跨越该类场地的首选结构形式。而我国地震灾害频发,在强震作用下,桥梁基础会同四周水体产生显著的地震动水力。地震动水力作为地震次生荷载,会改变桥梁结构的自振特性,从而影响其地震响应。国内外学者针对地震动水力的模拟以及对斜拉桥结构动力响应的影响进行了大量研究。LⅠAW 等[1]基于辐射波浪理论得出了地震动激励下圆形截面柱的动水力解析解,并认为水体对构件的影响可以通过改变其质量分布进行模拟;GOYAL 等[2]在考虑水、土等复杂边界条件与结构相互作用的基础上,提出了斜拉桥桥塔在地震激励下地震动水力的模拟方式;赖伟[3]基于辐射波浪理论推导出棱柱承台地震动水力的解析解,并通过实验进行了验证;LⅠ等[4]基于辐射波浪理论和ANSYS 软件中的流体元,通过曲线拟合给出了圆形墩和方形墩的附加质量表达式;JⅠANG 等[5]通过详细的数据拟合,提出了以横截面半径和浸没高度为主要参数的圆柱体动水力简化计算公式。但目前国内外对高桩承台群桩基础在考虑动水力时的地震响应问题研究较少,便于工程应用的高桩承台群桩基础动水力附加质量简便算法更是鲜有报道。在地震动水力对深水大跨斜拉桥地震响应影响方面的研究,张士博等[6]对斜拉桥桥塔进行了缩尺模型振动仿真试验研究,结果表明在真实海况下地震灾害来袭时,动水力主要由地震产生,且桥塔最大响应主要位于承台区域;李悦等[7]研究表明,地震动水力对斜拉桥的自振特性和动力响应会造成很大影响,特别是显著增大了主梁的纵向位移。斜拉桥主要震害表现为桥塔塔底承载能力不足引起的强度破坏以及因主梁梁端过大的纵向位移所导致与引桥梁体碰撞损伤甚至落梁等严重后果。针对适用于斜拉桥的减震措施,学者们开展了一系列研究。TSAⅠ等[8]针对黏滞阻尼器控制桥梁地震响应方面做了研究,并推导出有效的黏弹性阻尼器分析模型;陈应高等[9]以非等高三塔斜拉桥为控制对象,采用设置在两边塔处的黏滞阻尼器建立了全桥的减震体系,结果表明各个桥塔在地震荷载下的内力响应幅值均得到有效控制;阎武通等[10]以一种新型黏滞减震装置和黏滞阻尼器进行斜拉桥减震效果对比分析,结果表明2种装置均可有效降低主梁纵向位移响应幅值;熊柏林等[11]对半漂浮体系斜拉桥的黏滞阻尼器进行参数优化,得到了单一设防水准下斜拉桥的最优阻尼系数与阻尼常数。可以看出,大部分学者的研究成果都较为倾向采用黏滞阻尼器对中大跨斜拉桥进行减震控制,然而目前考虑地震动水力情况下采用黏滞阻尼器的斜拉桥减震控制研究仍鲜有报道。鉴于此,本文以某跨海斜拉桥为工程背景,将高桩承台基础分为承台与群桩2部分,各自采用不同简便方法计算地震动水力附加质量,分析多种设防水准下黏滞阻尼器选取不同设计参数时的减震效果,同时提出可靠的参数优化原则及推荐参数范围,研究成果可为不断涌现的深水斜拉桥的减震设计提供参考。
1 地震动水力附加质量模型
1.1 大尺寸构件附加质量模型
假设底部固定的悬臂圆柱体位于理想无黏性不可压缩水体中,水平地震波作用于柱底,忽略水体表面的自由波,则其运动方程为:

式中:Ms为结构的质量矩阵;Cs为阻尼矩阵;Ks为刚度矩阵;us表示结构的加速度列向量;us表示速度;us表示位移,ug表示地面加速度;fw表示地震动水力。
根据水体的控制方程和边界条件,即可推导圆柱体在深度z处的精确动水力解[12]:
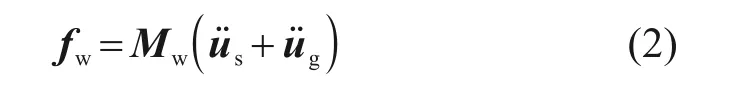
其中:
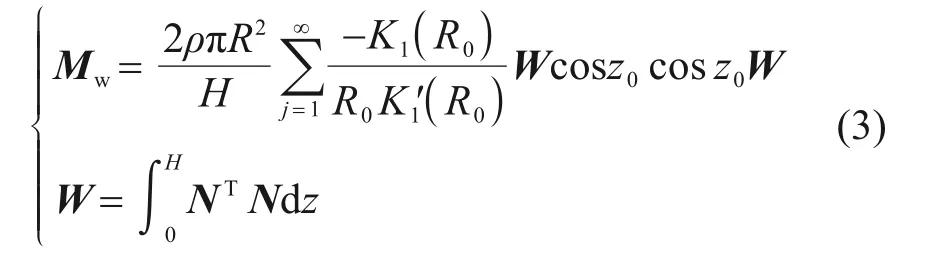
式中:Mw为动水力等效质量矩阵;N为单元的形函数;T表示转置计算。
将式(2)代入式(1)即可得到考虑地震动水力作用的结构运动方程:

在式(3)中,Mw为水体附加质量的精确解,WANG 等[13]为便于工程应用,基于利用刚性柱法进行简化的精确解Mw进行拟合,进一步简化为:
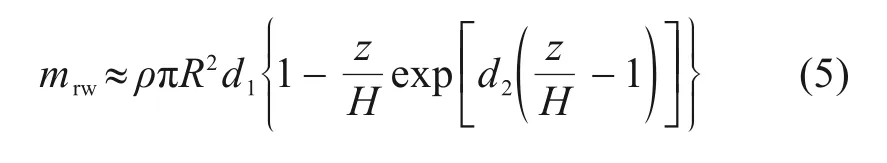
其中:
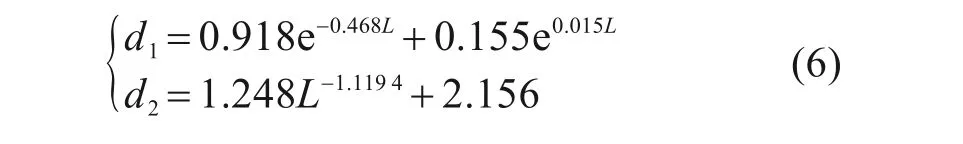
式中:L=2R/H,为圆柱体直径与水深之比,0.2≤L≤2。
赖伟[3]通过试验并采用最小二乘法拟合,得到单位高度矩形截面的动水力附加质量与圆形截面动水力附加质量的等效换算系数:
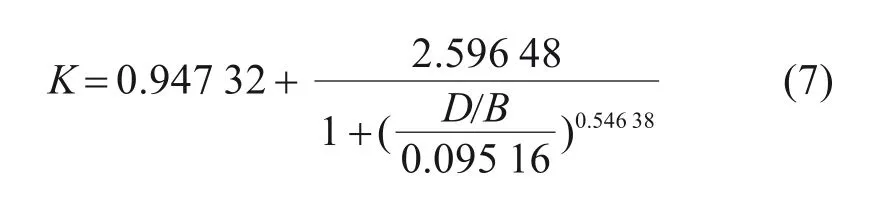
式中:D为矩形截面正面迎击水体的宽度;B即为D邻边的宽度。适用于0.1≤D/B≤10。
根据式(5)~(7)即可计算大尺寸矩形截面构件的动水力附加质量。
1.2 小尺寸构件附加质量模型
假定不同水深下柱-水的相互作用相同,YANG 等[14]将实际中的三维柱-水耦合系统简化为二维柱-水耦合模型计算单桩上的地震动水力。对于高桩承台群桩基础,桩与桩之间的距离和角度对整个群桩基础地震动水力的影响不容忽视。因此,YANG 等[15]在上述研究的基础上进一步探究了群桩结构中半径为r的单桩上动水力附加质量系数为:
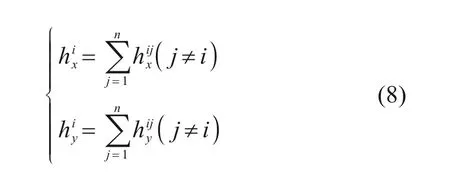
通过式(8)可计算出单桩受到其余各桩的影响,则群桩中任意单柱上的动水力计算公式为:
2 工程概况及计算模型
某主跨为400 m 的双塔双索面组合梁斜拉桥,跨度布置为(70+70+130+400+130+70+70) m,桥梁全长940 m,见图1所示,采用半漂浮体系。
主梁全长采用混凝土桥面板+槽形钢箱梁的组合梁结构,主梁梁宽16 m,梁高4.5 m。二期恒载取133.4 kN/m。全桥共72 对斜拉索,采用镀锌平行钢丝拉索,空间双索面扇形布置。桥梁主塔高169.3 m,塔柱间设2 道横系梁,塔底设置塔座,塔座下承台高6 m,承台顶面为最高通航水位。本文不考虑地震动桩-土效应,仅将各桩基础在冲刷线处固结,主塔动水力附加质量计算结果见表1。
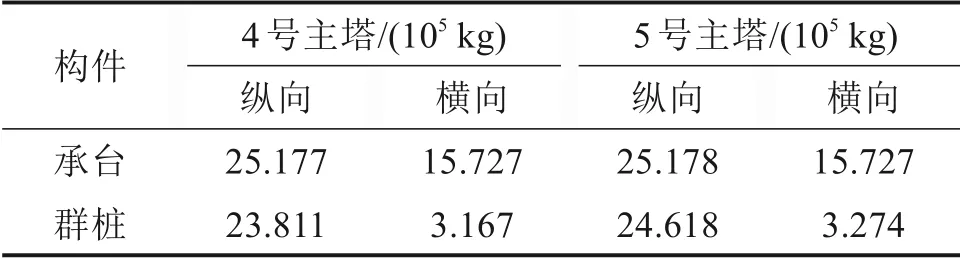
表1 动水力附加质量计算结果Table 1 Dynamic hydraulic additional mass
本文采用非线性有限元软件OpenSees 建立该桥简化脊梁式动力分析模型,见图2所示。在脊梁式模型中较为关键的是截面特性及质量的准确模拟,将钢混组合梁等效转换为混凝土进行计算。主梁、各墩/塔及高桩承台基础均采用弹性梁单元(Elastic beam column element)模拟,斜拉索采用桁架单元(Truss element)模拟。通过建立墩-梁、塔-梁自由度之间的主从关系(EqualDOF),耦合主梁2和3 方向的平动和绕1 方向的转动,简化模拟支座的约束作用。桥梁阻尼体系模型中,设有4个黏滞阻尼器,每座桥塔下2 个,采用零长度单元(Zerolength element)模拟。模型中,该单元的两端节点坐标重合,坐标均位于主塔下横梁跨中正上方主梁上,即单元一端节点为主梁节点,另一端节点与桥塔下横梁跨中节点刚性耦合。
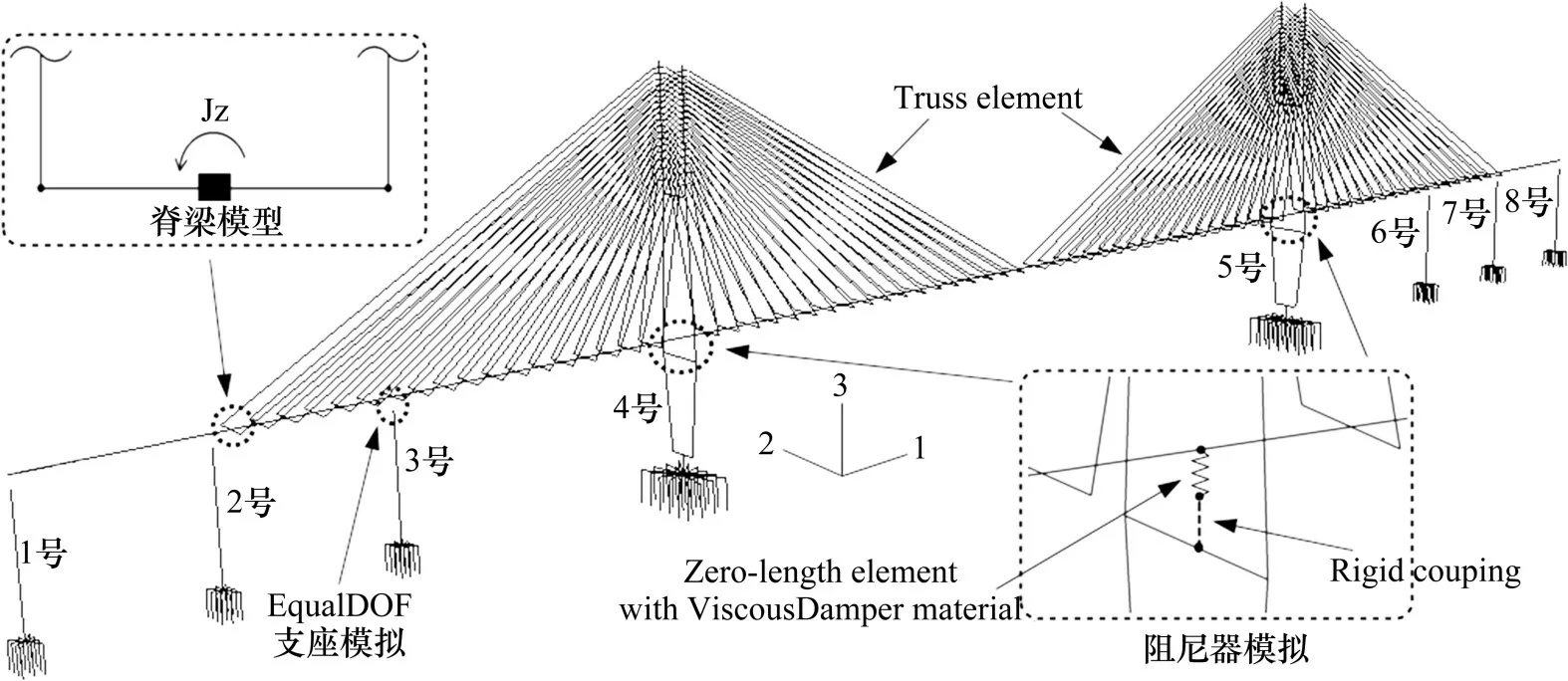
图2 斜拉桥有限元模型Fig.2 Finite element model of cable-stayed bridge
采用子空间迭代法计算考虑和忽略地震动水力2种情况下桥梁的自振特性,并求出斜拉桥在考虑地震动水力时的自振频率fl与忽略地震动水力时的自振频率f的比值fl/f,其无水情况下前4 阶振型及2种情况下相同振型所对应的自振频率见表2。
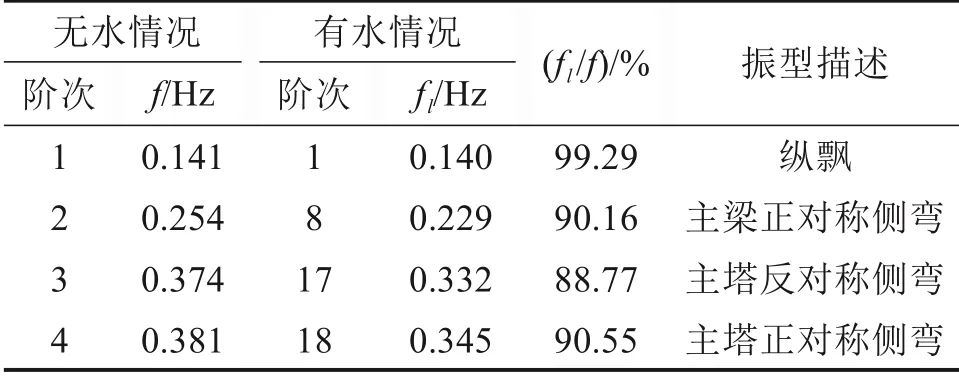
表2 斜拉桥动力特性Table 2 Dynamic characteristics of cable-stayed bridge
由表2 可知,该斜拉桥第1 阶振型为纵飘,结构的基本周期在2种情况下均约为7.1 s,属于低频振动结构。这符合半漂浮体系斜拉桥的特征,验证了本文有限元模型的有效性,同时此特征对减小结构的地震响应是有利的,但会产生较大的纵向位移。此外,由于考虑地震动水力后基础结构动水附加质量的影响,使得该斜拉桥无水情况下除第1阶振型外其余振型均在考虑地震动水力情况下的自振特性中滞后,表明地震动水力会显著影响斜拉桥的频率分布。且考虑地震动水力后,相同振型的自振频率也均有所降低,这与文献[1,3,6-7]中的结论一致。验证了地震动水力会对结构的自振特性造成一定影响,同时也验证了本文地震动水力模拟的正确性。水体的存在对斜拉桥桥体结构自振特性的影响不容忽略。
3 计算参数
3.1 地震动输入
本文基于《铁路工程抗震设计规范(2009 版)》(GB 50111—2006)中的设计反应谱选取实测地震动记录。但由于该反应谱下降段范围较小,一般适用于中小跨梁式桥、拱桥等高基频结构,而该跨海斜拉桥前5 阶自振周期均大于2 s。故依照文献[16]对规范中设计反应谱下降段进行修正,将设计地震加速度放大系数β的周期范围拓展到10 s,如式(10)所示。
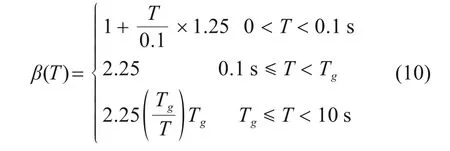
式中:T为自振周期,s;Tg为特征周期,s;参照相关规范,Tg=0.45 s。
根据设计地震下的加速度反应谱曲线在PEER数据库选取了4 条实测地震记录并人工模拟1 条地震记录作为输入,其加速度反应谱对比曲线如图3所示。由图3 可知,选取的4 条地震波的平均反应谱与设计反应谱在长周期段基本吻合,在结构基本周期处高出目标反应谱9.8%,由此可判断输入地震波的合理性。根据相关铁路工程抗震细则中三水准设防要求,5 条地震加速度时程曲线经规格化处理后,将其PGA 分别调整为0.05g(多遇地震)、0.15g(设计地震)和0.32g(罕遇地震)后输入。

图3 加速度反应谱对比曲线Fig.3 Comparison curves of acceleration response spectrum
3.2 黏滞阻尼器
采用OpenSees 材料库中基于Maxwell 模型开发的ViscousDamper Material 模拟黏滞阻尼器力学特性,其力学本构关系为:
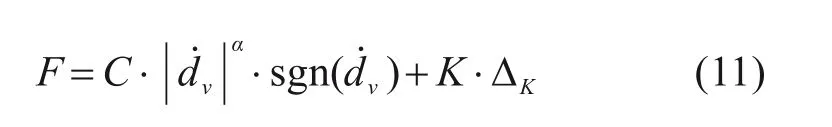
式中:F为阻尼力;C为阻尼常数;α为阻尼指数;ΔK和dv分别为阻尼器自身弹性变形和阻尼力做功的距离;K为阻尼器材料刚度,在分析时,为凸显阻尼器的阻尼效果,K一般输入较大值,但这将导致阻尼器减震效果偏于不真实和最终选定的阻尼器参数偏于不保守[17],本文取K=100C。
参考国内外斜拉桥黏滞阻尼器常见设计参数以及以往分析经验,本文选择阻尼指数α以0.1 为步 长, 从0.2 增 大 到0.8, 阻 尼 常 数C以2 000 kN·(m/s)-α为步长,从2000 kN·(m/s)-α增加到10 000 kN·(m/s)-α。
4 结果分析
为探究考虑地震动水力后黏滞阻尼器各力学参数对减震效率的影响,采用工程实际中广泛使用的阻尼体系布置方案,即在桥塔与主梁处安装4个黏滞阻尼器,每座桥塔下设置2个,对该桥做考虑非线性边界条件的动力时程分析。将5条地震波沿桥梁纵向输入,计算采取不同阻尼器参数时斜拉桥在不同地震峰值加速度下主梁梁端纵向位移及4 号桥塔塔底内力,并求取它们在5 条地震动激励下响应幅值的平均值。至此引入响应比例指标,即以减震控制结构与非阻尼体系结构二者的地震响应均值之比,用以反映减震效果。其比值越小表明减震效果越好,比值大于1.0 则表示产生不利影响。在上述5条地震波作用下,黏滞阻尼器不同参数对该跨海斜拉桥主要地震响应比例的影响见图4~6。
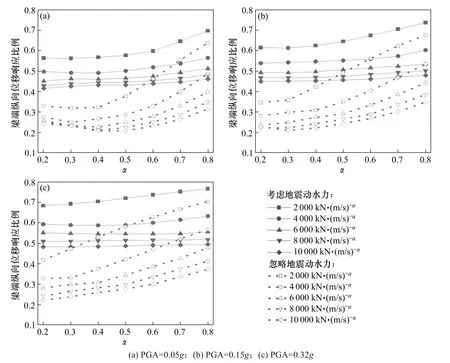
图4 梁端纵向位移响应比例Fig.4 Ratio of longitudinal displacement response
3 种地震设防水准下,黏滞阻尼器参数对主梁梁端纵向位移响应比例的影响如图4 所示。由图4可知:有水情况下,通过设置合适的黏滞阻尼器参数,各级设防水准下均可将主梁梁端纵向位移响应减至接近非阻尼体系结构的50%,可见黏滞阻尼器在对斜拉桥位移响应控制方面卓有成效。但考虑地震动水力时,相同参数阻尼器的减震效果显著低于忽略地震动水力时的减震效果,表明忽略地震动水力会大大高估黏滞阻尼器对斜拉桥主梁位移控制能力。总体来说,考虑地震动水力与否,黏滞阻尼器对梁端纵向位移的减震效果均随阻尼指数α的增大而衰减,随阻尼常数C的增加而提高。值得注意的是,考虑地震动水力时调节α对减震效率影响不大,建议通过调节阻尼器C大小以达到目标主梁纵向位移减震率。
3 种地震设防水准下,黏滞阻尼器参数对4 号桥塔塔底纵向弯矩响应比例影响如图8所示。由图5 可知:从总体上看,有水情况下的减震效果略强于无水情况下的减震效果。各设防水准下,考虑地震动水力的结构体系最佳塔底纵向弯矩响应比例均能小于0.6。不同于无水情况下过小α值搭配过大C值的黏滞阻尼器在较低设防水准下对塔底弯矩响应产生不利影响,考虑地震动水力后黏滞阻尼器的使用对减小塔底纵向弯矩响应在各级设防水准中均起积极作用。但值得关注的是,考虑地震动水力后,在各级设防水准下,塔底弯矩减震效率随阻尼器参数的变化规律所呈现出的差异:首先,如图5(a)所示,若阻尼常数较小[C≤4 000 kN·(m/s)-α],塔底纵向弯矩响应比例随着α的增大而增大;若阻尼常数较大[C>4 000 kN·(m/s)-α],则塔底纵向弯矩响应比例随α的增大先增大后减小。其次,在PGA≥0.15g后,塔底纵向弯矩响应比例随α的增大而增大,且增幅较小。

图5 塔底纵向弯矩响应比例Fig.5 Response ratio of longitudinal bending moment at the bottom of pylon
由上述分析可知,在对考虑地震动水力的跨海斜拉桥采用黏滞阻尼器进行减震控制时,阻尼器各项参数的选取要关注当前的设防水准,不同的设防水准决定结构内力减震效率与阻尼器参数的关系单调与否。需注意的是,如图6所示,考虑地震动水力后塔底纵向剪力响应比例显著高于忽略地震动水力的响应比例,虽然随着地震设防水准的提升而二者的差值在逐渐减小,但从图中可以看出,在3种设防水准下考虑地震动水力后的各阻尼器参数组合中,纵向剪力响应比值大于1.0 的占大多数,这表明考虑地震动水力后黏滞阻尼器对塔底纵向剪力大概率将产生不利影响,盲目地增加或减小阻尼器参数将导致塔底纵向剪力急剧增大。因而在一定的设防水准下,可根据目标减震率粗略确定阻尼常数C的初值,然后探寻塔底弯矩减震效果随阻尼指数α的变化趋势,具体参数调整选取原则如下:
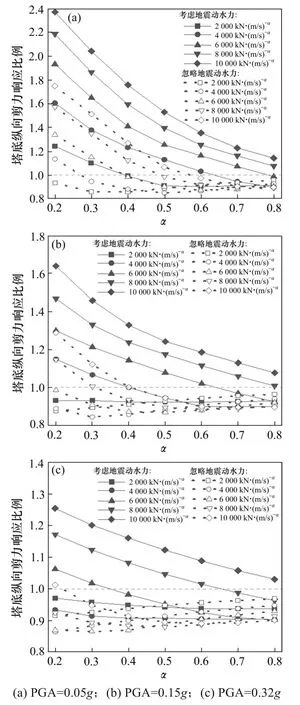
图6 塔底纵向剪力响应比例Fig.6 Response ratio of longitudinal shear at the bottom of pylon
若塔底纵向弯矩响应比例随α的增大先减小后增大,则说明对于当前设防水准条件C偏大,需减小C直到响应比例随α的增大而增大,且弯矩响应比例尽量介于0.6~0.7 范围。此时C适用于目标设防条件,之后选取合适的α即可达到目标减震率。
5 结论
1) 地震动水力对斜拉桥结构的自振特性会产生影响。虽在考虑和忽略地震动水力2 种情况下,结构的第1阶振型一致且基频相差无几,但地震动水力会对阻尼器减震效果造成显著影响,不容忽略。
2)通过对比考虑和忽略地震动水力2 种情况,结果表明忽略地震动水力会高估黏滞阻尼器对斜拉桥主梁纵向位移的控制能力。并且忽略地震动水力会造成黏滞阻尼器在实际有水情况下产生过大的阻尼力对塔底内力产生不利影响,有悖于减震控制初衷。
3) 跨海斜拉桥结构考虑地震动水力后,建议先根据减震目标粗略计算出阻尼常数C的初值,然后分析塔底内力减震效果随阻尼指数α的变化趋势,进行黏滞阻尼器参数选取。依据该原则,考虑地震动水力的跨海斜拉桥采用黏滞阻尼器进行减震控制时,阻尼常数C宜控制在4 000~6 000 kN·(m/s)-α,阻尼指数α宜控制在0.5~0.7 范围内。如此,在3种设防水准下可保证主梁梁端纵向位移最低40%减震率,主塔塔底纵向弯矩最低30%减震率。
