螺纹桩中性点位置及轴力计算方法研究
2022-08-29周芝林
周芝林
(珠海香海大桥有限公司,广东 珠海 519000)
挤密螺纹桩(以下简称螺纹桩),属于变截面异形桩,因其桩-土接触面螺纹的存在,大大提高了抗压承载力,在工程中得到了较多的应用[1-2]。螺纹桩在成桩工艺上具有多种形式,国内已有桩型为螺杆桩、变截面螺纹桩与全螺旋灌注桩[3-4]。吴敏等[5]对比了螺纹桩与普通直桩,由于螺纹结构的存在,有效提高了螺纹桩的单桩承载力。郑军锋等[6]基于新建兴泉铁路黄塘车站路堤下螺纹桩复合地基桩土应力比现场试验指出,桩土应力比实测数值在1.06~3.47之间。螺纹桩网复合地基在填土荷载作用下桩身会出现负摩阻力,聂如松等[7]对负摩阻力作用下的单桩承载性状进行了研究。姜文雨等[8]提出修正的桩侧摩阻力分布模式,并对中性面位置进行了求解。叶观宝等[9]对填土条件下桩侧负摩阻力进行了研究。聂如松等[10]对比研究了不同桩土接触面粗糙程度与不同桩体泊松比对桩侧摩阻力的影响。中性点往往与负摩阻力的产生有关,中性点通常定义为桩身上正负摩阻力分界点。在中性点位置处,桩土相对位移为0,此时桩身轴力达到最大值,因此通过确定中性点位置便可确定桩身最不利位置。本文基于荷载传递法建立螺纹桩的基本微分方程,推导出中性点位置、桩身轴力及总负摩阻力的计算式,为螺纹桩的研究提供理论支持。
1 螺纹桩桩-土简化力学模型
1.1 螺纹桩力学模型
如图1所示,与螺纹桩计算有关的直径参数主要为:外径D,对应半径为R;内径d,对应半径为r;等效直径d′。等效直径为假想直径,等效直径由式(1)确定。
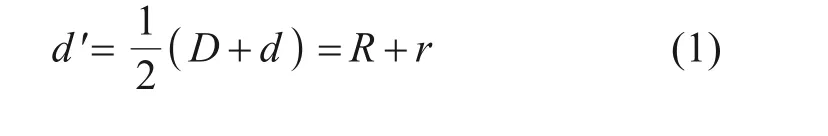
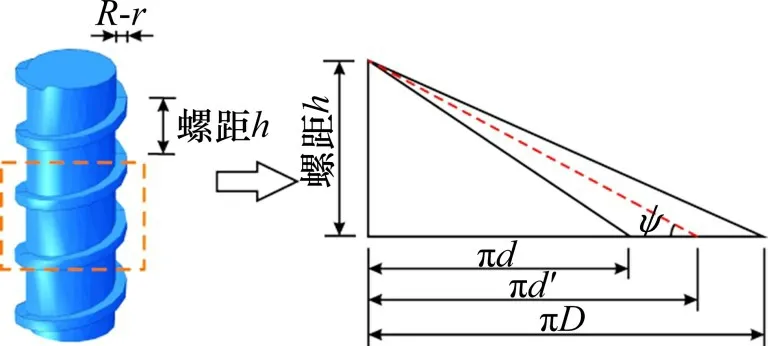
图1 螺纹桩几何参数示意图Fig.1 Geometric parameters of screw pile
螺纹升角用字母ψ表示,根据螺纹升角的定义:
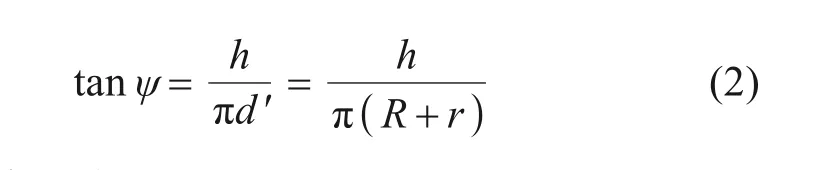
式中:h为螺纹间距。
螺纹桩复合地基在均布荷载作用下的桩-土受力如图2所示。计算模型做如下假定:
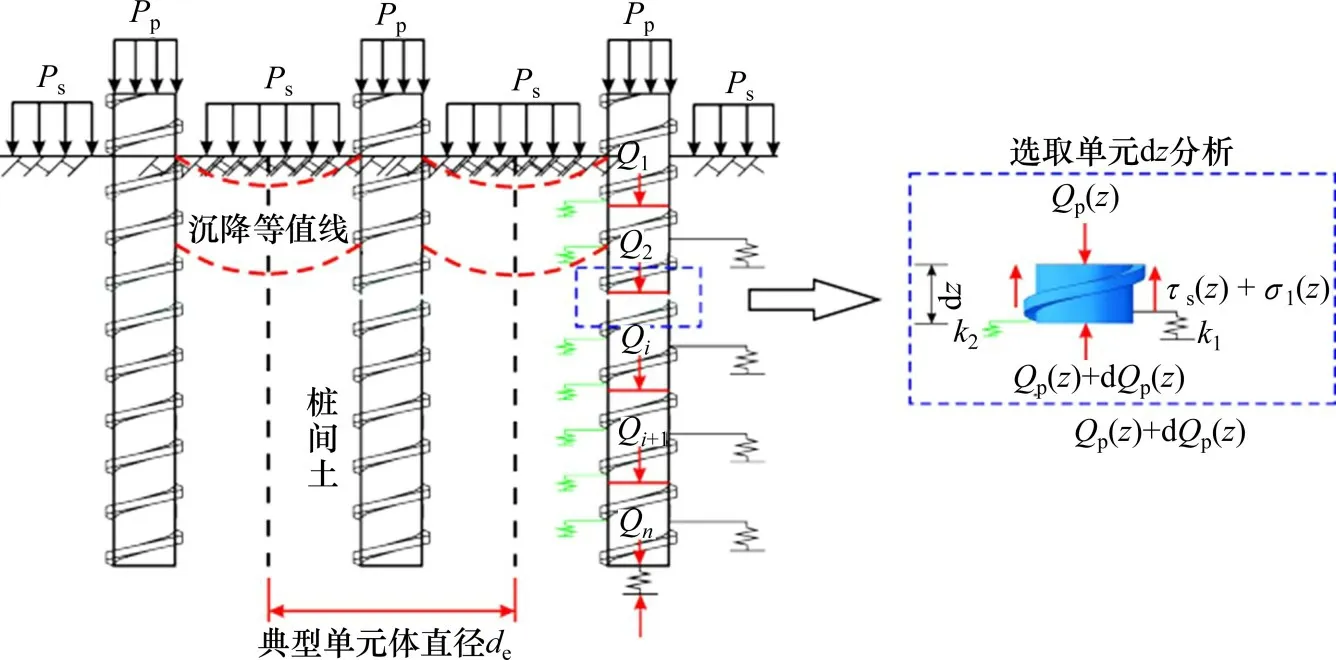
图2 螺纹桩桩-土体系力学模型简图Fig.2 Mechanical model of screw pile and soil system
1) 按一维问题求解,桩、桩间土的位移与压力仅随深度变化,即同一水平面上桩间土沉降值相同;2) 螺纹面上作用力为竖向阻力,同时忽略偏心力的影响;3) 荷载作用下桩周土体的沉降为竖直方向的一维线性变形,桩端土满足Winkler 地基模型;4) 将路堤荷载经调整后作用在桩顶与桩间土的荷载等效简化为均布荷载Pp和Ps。
将螺纹桩划分为n个弹性节段,弹性节段与桩周土采用非线性弹簧连接,通过弹簧的应力-应变关系表示桩土的荷载传递。
取螺纹桩单元dz分析,如图2所示,不计螺纹侧表面摩阻力因螺纹桩外径和内径的差异导致桩身轴力的差异,计算桩身轴力时,侧摩阻力引起的轴力增量统一利用螺纹桩内径计算,则螺纹桩单元dz受力平衡如式(3)所示。
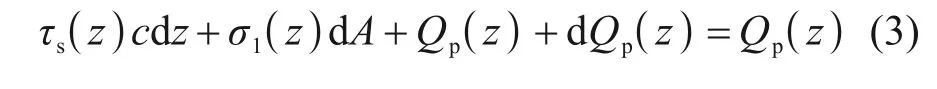
式中:τs(z)为侧摩阻力;σ1(z)为螺纹面竖向阻力;c为内径对应的周长,c=2πr;dA为dz长度螺纹面面积[11]。
dA计算式如式(4)所示:
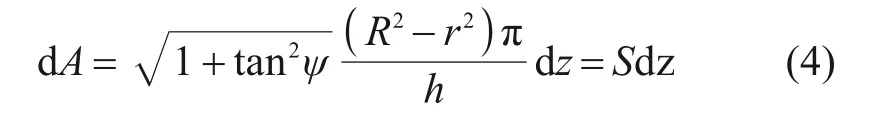
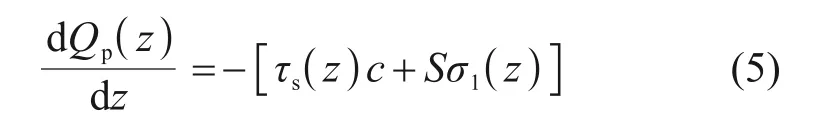
螺纹桩单元dz的位移量dsp(z)为
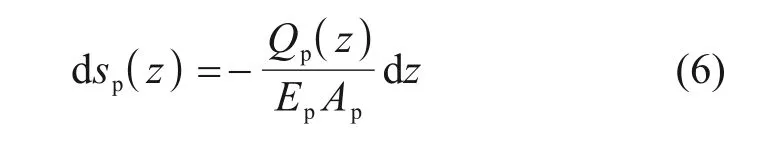
式中:Ep为螺纹桩桩身材料弹性模量;Ap为螺纹桩内径对应截面面积,Ap=πr2;其余符号同前。将式(5)代入式(6)可得到
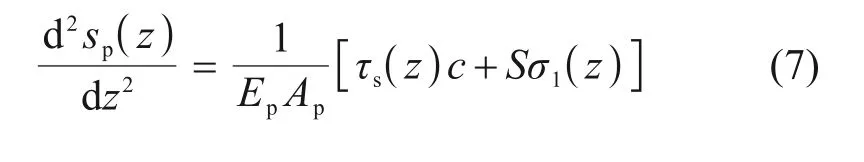
式(7)为螺纹桩桩土体系荷载传递基本微分方程。
1.2 桩-土荷载传递模型
为研究方便,采用双折线模型来描述桩侧摩阻力与相对位移、螺纹面竖向阻力、桩端压力与地基土相对位移的关系[11](其中桩侧摩阻力与桩土相对位移之间的关系采用佐滕悟模型),如图3所示。
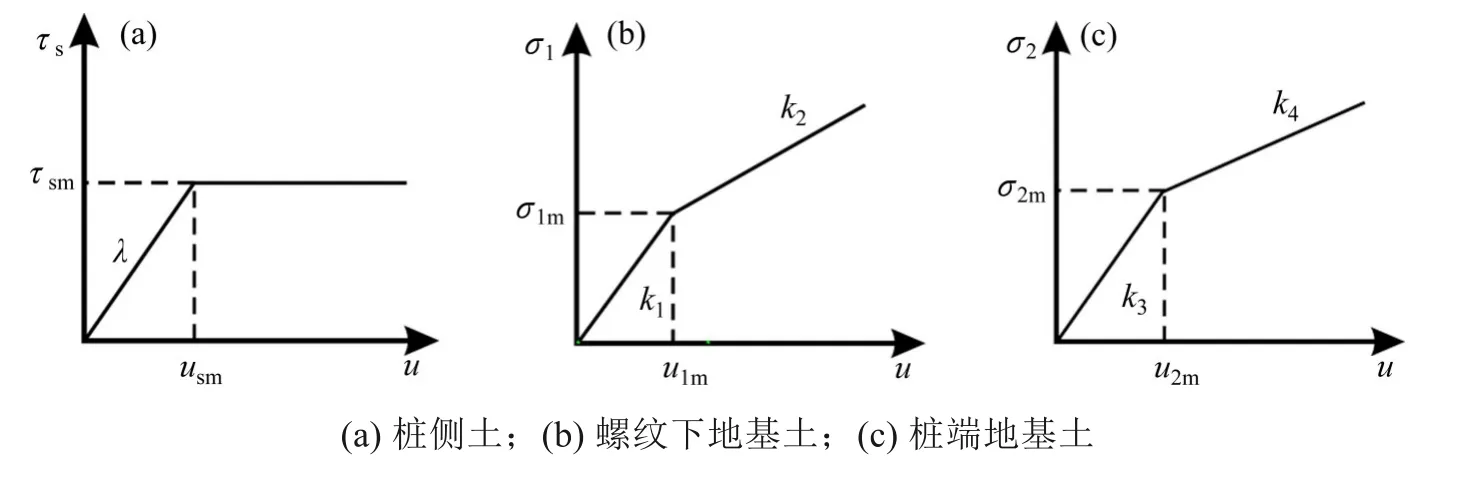
图3 双折线数学模型Fig.3 Mathematical model of double polyline
桩侧摩阻力与桩-土相对位移的关系式如式(8)所示:
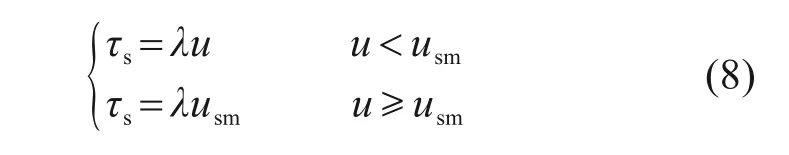
螺纹面竖向阻力与桩-土相对位移的关系式如式(9)所示:

桩端压力与桩-土相对位移的关系式如(10)所示:
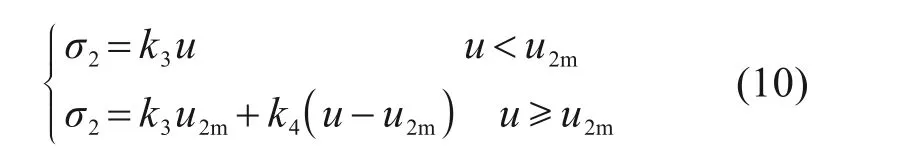
式中:λ为桩侧土发生屈服的剪切刚度系数;k1和k2为螺纹下地基土发生屈服前后的压缩刚度系数;k3和k4为桩端土发生屈服前后的压缩刚度系数;usm,u1m和u2m分别为桩侧土、螺纹下地基土和桩端土发生弹性变形时的极限值。
桩间土顶部沉降为ss上,桩间土底部沉降为ss下,土体沉降深度方向斜率为:

式中:l为桩长。
图4为螺纹桩复合地基示意图,螺纹桩的外径为D,螺纹单桩的加固范围直径为de,半径为re,螺纹桩复合地基受到上部大面积填土的堆载作用。
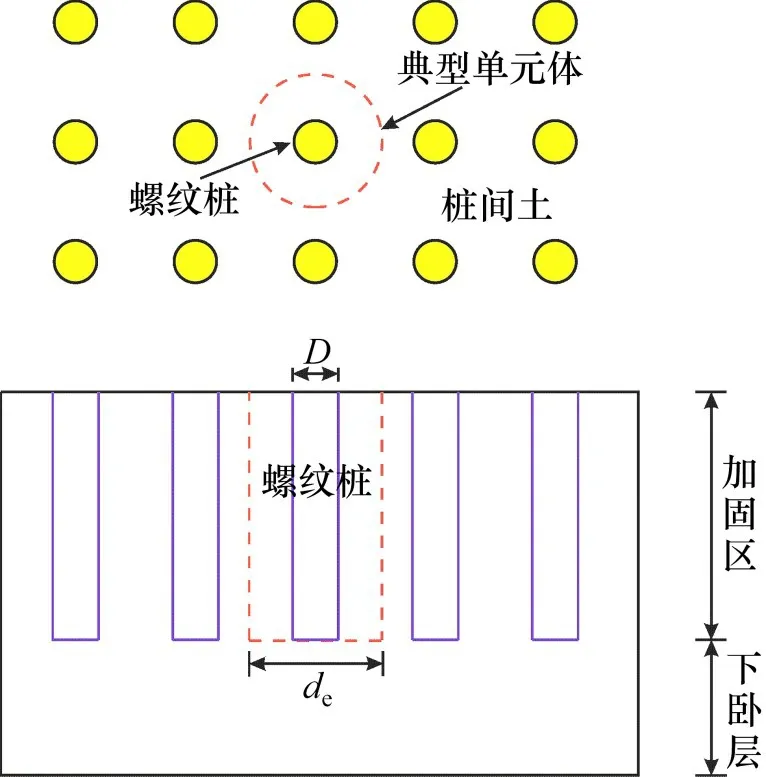
图4 螺纹桩复合地基示意图Fig.4 Diagram of screw pile composite foundation
取单个螺纹桩桩体及其影响范围内土体所形成的同心圆柱体作为典型单元体进行分析。柔性基础作用下,群桩典型单元体的外侧边界剪应力和径向位移为0,因此可认为典型单元体的受力变形特征能代表群桩复合地基的受力变形特征。典型单元体的直径可由式(12)确定。

式中:sd为桩间距,cg由布桩方式确定,等边三角形布桩取1.05,正方形布桩取1.13。
2 螺纹桩荷载传递解析解
2.1 螺纹桩轴力计算方法
螺纹桩复合地基中桩体发生弹性变形,桩侧土(包括螺纹下地基土)与桩端地基土的变形随上部荷载的大小主要分为弹性变形阶段、弹塑性变形阶段与塑性变形阶段。在上部荷载作用下,由于螺纹桩变形模量远大于桩间土变形模量,因此荷载向桩顶集中,即桩的应力集中效应。随着荷载继续增加,桩的应力集中效应更加明显,此时桩开始向褥垫层刺入。随着荷载的持续增加,桩侧摩阻力发挥至极限值,桩端阻力开始发挥,桩底向下刺入下卧层,此时桩顶与桩端附近的土体进入塑性状态。简化的桩土体系荷载传递如图5 所示,P为复合地基均布荷载,塑性区桩土相对位移u≥max(usm,u1m)。由图5可知,桩侧摩阻力分布模型为分段分布,其中:1)0≤z≤z1为负摩阻力塑性区,相对位移为u1;2)z1≤z≤z2为弹性区,相对位移为u2;3)z2≤z≤l为正摩阻力塑性区,相对位移为u3。z0为中性点所在深度,桩土相对位移u(z)由式(13)表示:
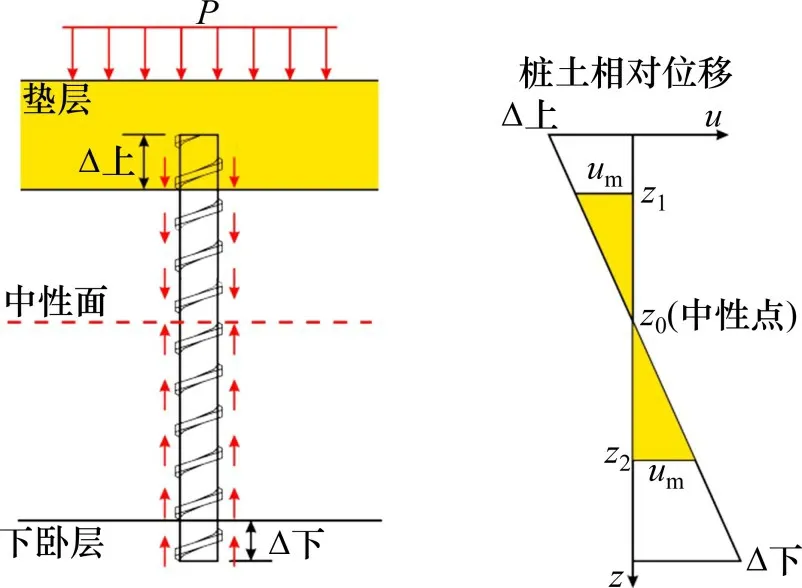
图5 桩土体系的荷载传递Fig.5 Load transfer of pile-soil system
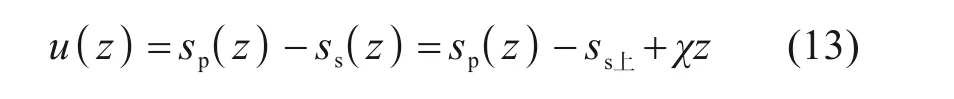
式中:sp(z)为桩体位移;ss(z)为土体位移。
将式(13)分别对z取1阶导数与2阶导数:
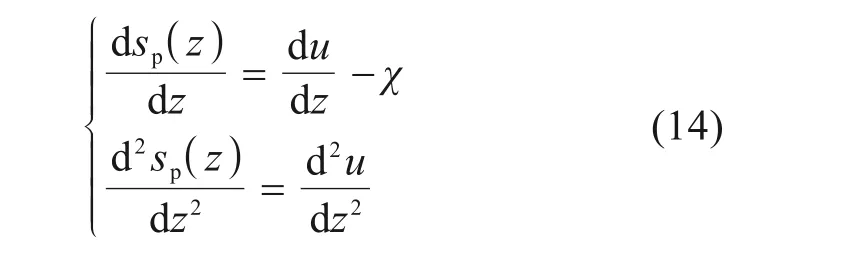
令usm=u1m=um,螺纹桩桩土体系荷载传递基本微分方程如式(15)所示:
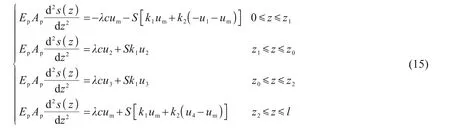
为了表达的简洁性,令:
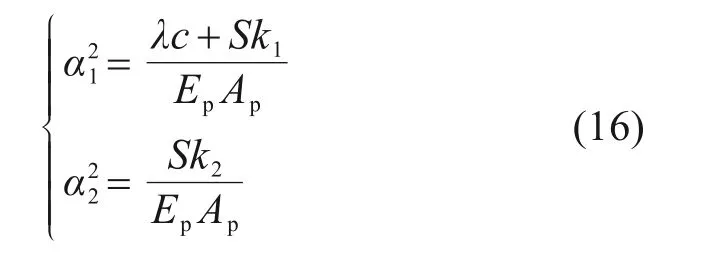
将式(16)代入式(15):
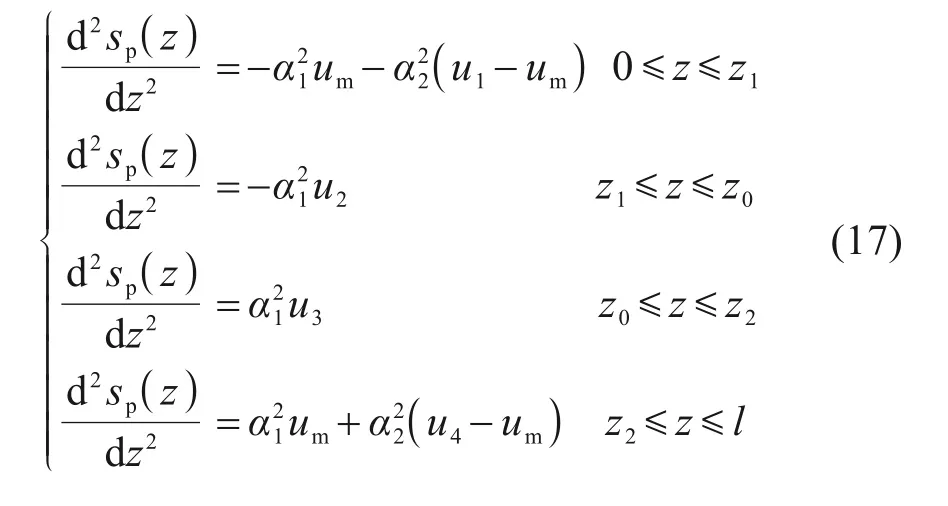
结合式(14)将式(17)化为下式:
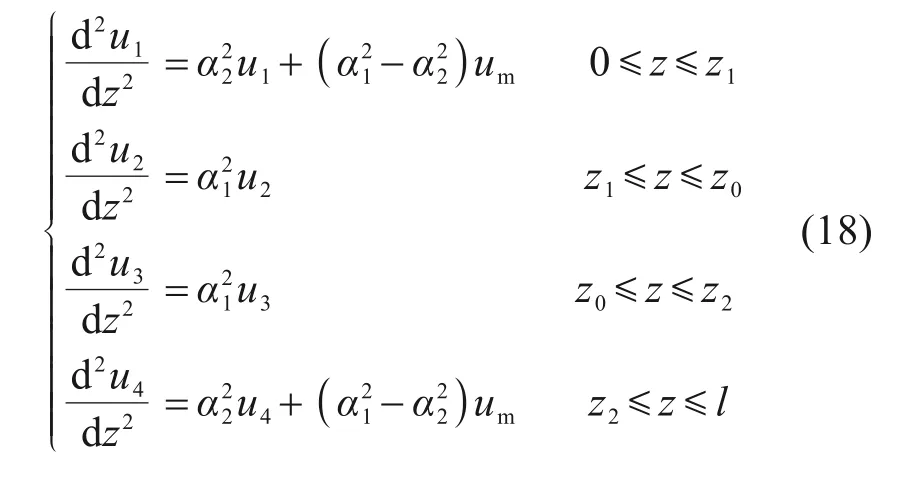
C1~C8为待定系数,由边界条件与连续条件确定。边界条件如式(21)所示:
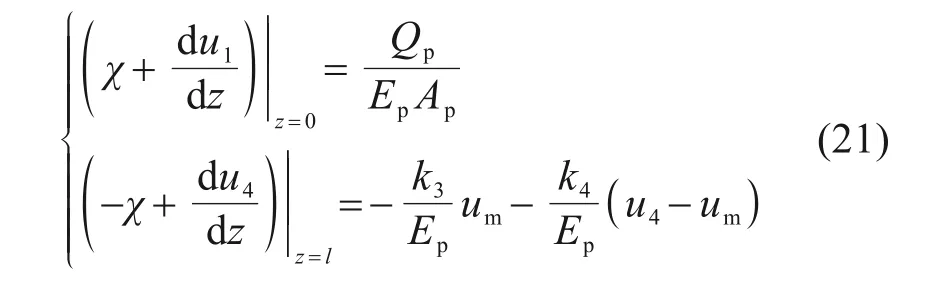
由连续性条件可知:
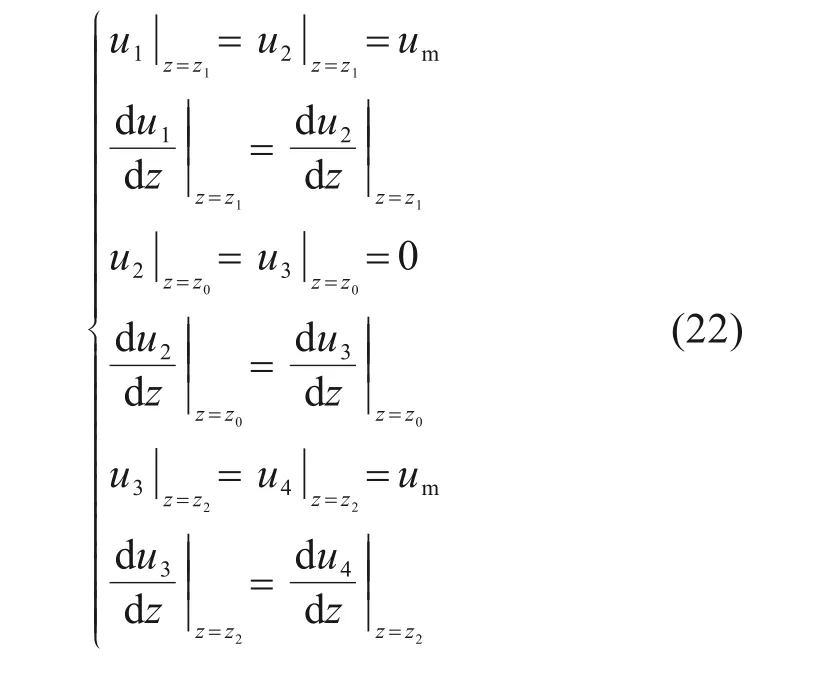
桩身轴力表达式如式(23)所示:
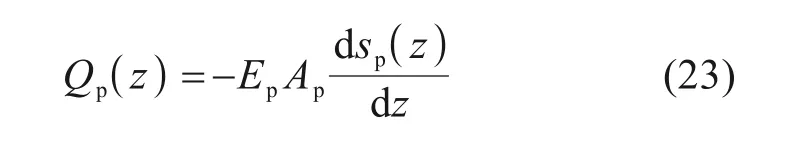
式(18)的通解与通解的1 阶导数如式(19)与式(20)所示:

可分阶段求解出螺纹桩桩身轴力。
2.2 复合地基桩土差异沉降
在螺纹桩复合地基中分别选取桩与桩间土单元dz分析,参考图5可知负摩阻力条件下桩单元dz的竖向力平衡条件为:
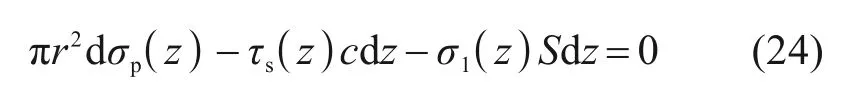
可得:

同理可得桩间土:
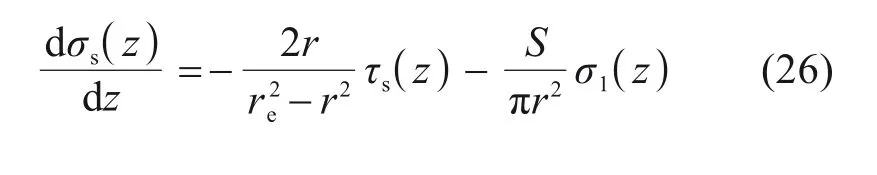
式中:σp(z)和σs(z)分别表示桩顶与桩间土单元dz的竖向均布荷载。
将桩侧摩阻力分段表达式代入式(25)与式(26)可得:
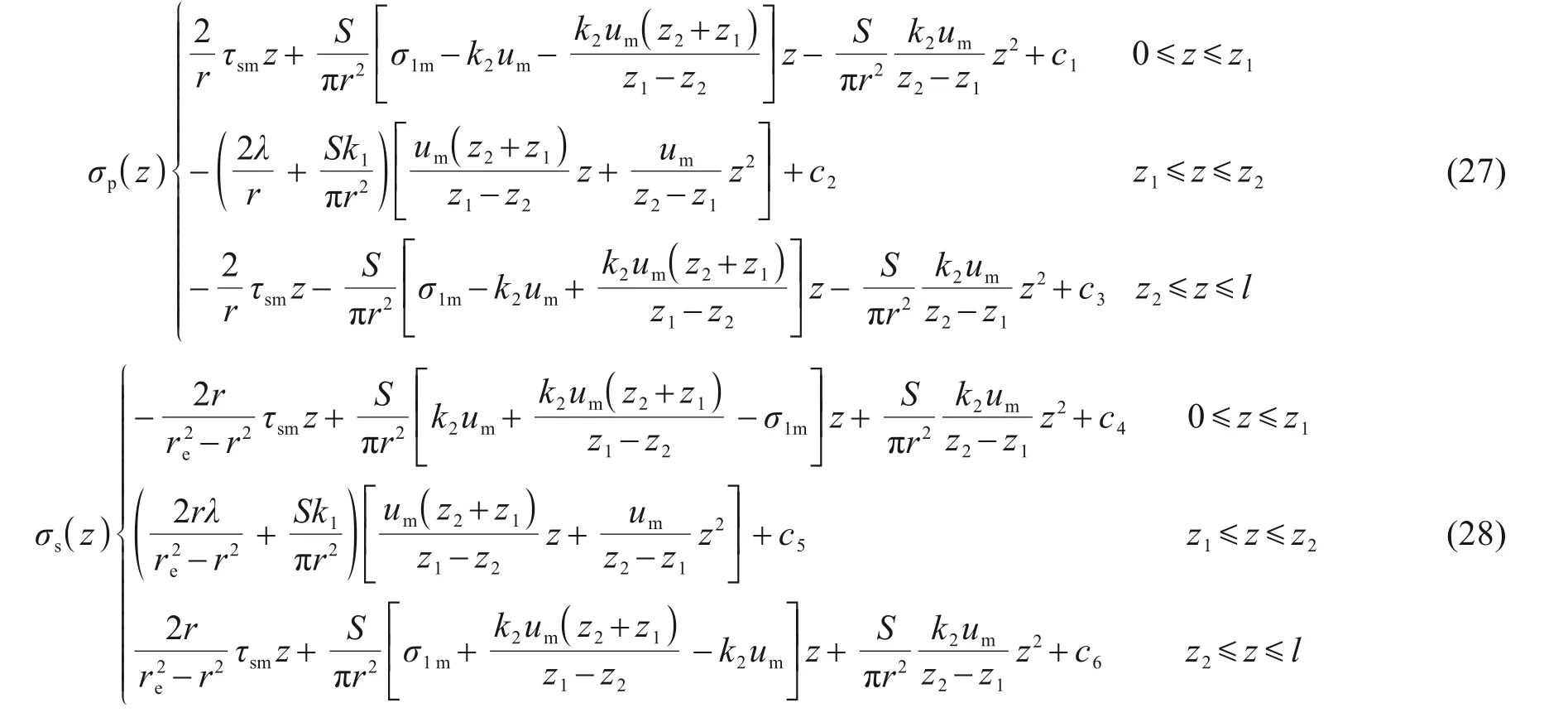
c1~c6为待定系数,由边界条件(29)与连续条件(30)确定。
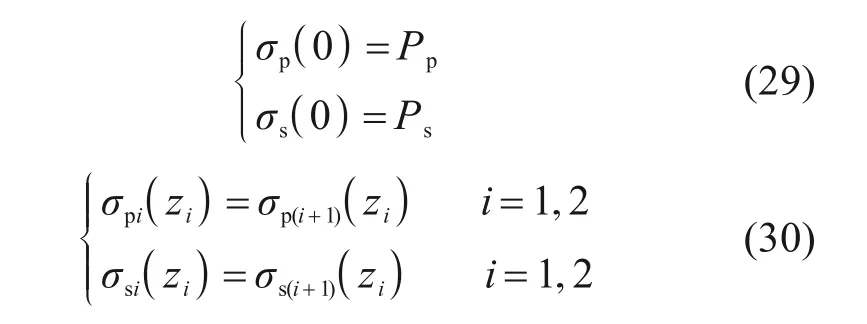
荷载作用下桩顶与桩底的竖向刺入变形量表示为[21,24]:
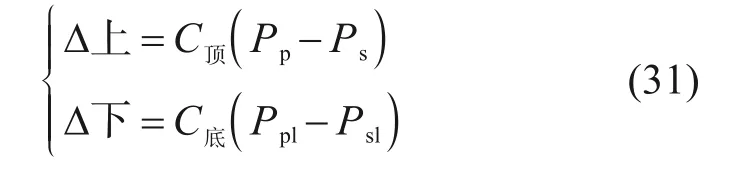
式中,C顶和C底分别表示桩顶作用在垫层与桩底作用于下卧层时单位压力的竖向刺入量,由式(32)求出[27];Ppl和Psl分别表示桩底应力与桩底平面处桩间土应力。
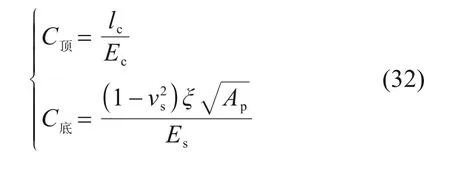
式中:lc和Ec分别为褥垫层厚度与变形模量;vs和Es分别为下卧层变形模量和泊松比;ξ为沉降影响系数,取值范围为0.85~1。
螺纹桩复合地基桩顶总荷载由桩与桩间土共同承担。
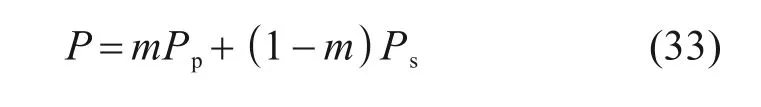
式中:m=Ap/Ae为螺纹桩面积置换率。
由图5可知:
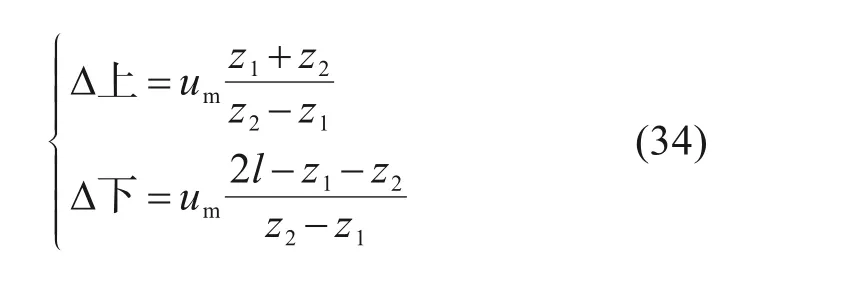
联立式(32)~(34)可得:
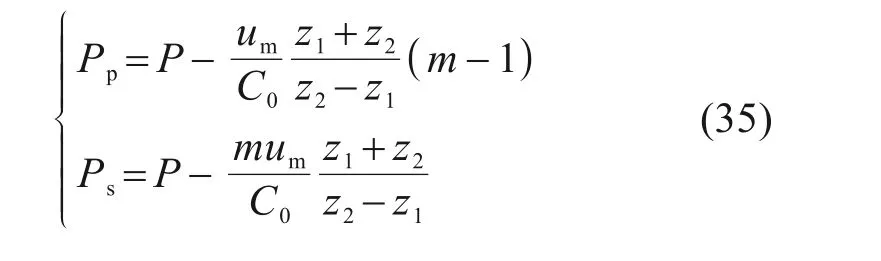
中性点上、下土体的压缩量s上与s下由式(28)代入桩间土的应力-应变关系并积分求出。
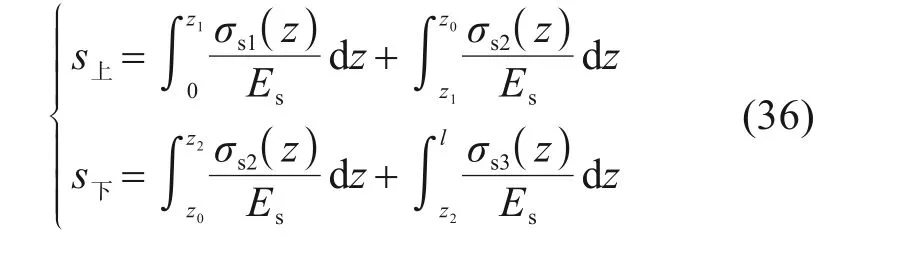
由中性点上、下土体的压缩量分别与螺纹桩的上、下刺入变形量相等可求出z1和z2。
3 方法验证及因素分析
3.1 螺纹桩数值模型建立及验证
螺纹桩数值计算模型如图6所示,模型中桩长l=6.0 m,螺纹间距L=0.3 m。路堤采用分层法进行填筑,每层填筑高度为0.6 m。
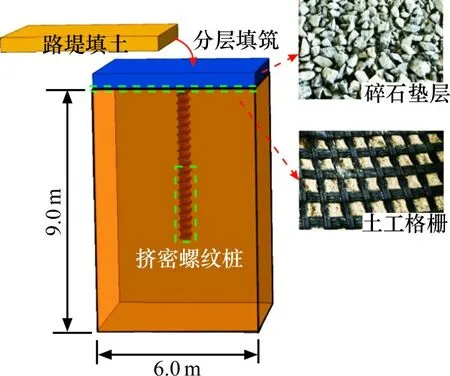
图6 数值分析模型Fig.6 Model of numerical analysis
土工格栅采用界面约束的嵌入接触方式,土工格栅作为嵌入区(Embedded region),嵌入到土体与碎石垫层间。采用HyperMesh 软件对螺纹桩网格进行划分,将桩-土接触部位划分为六面体网格,网格划分如图7所示,土工格栅采用四节点膜单元M3D4,其余部件采用八节点积分实体单元C3D8。在桩-土界面设置面-面摩擦接触,摩擦因数取为tan(0.65φ)(φ为地基土内摩擦角)。地基土与路堤土结构层选用理想弹塑性模型,其破坏准则采用Mohr-Coulomb 本构关系。螺纹桩、碎石垫层与土工格栅采用线弹性材料。计算参数是参考了文献[12-13]的变形参数经试算后确定,强度指标参数依据室内试验获取,具体如表1所示。
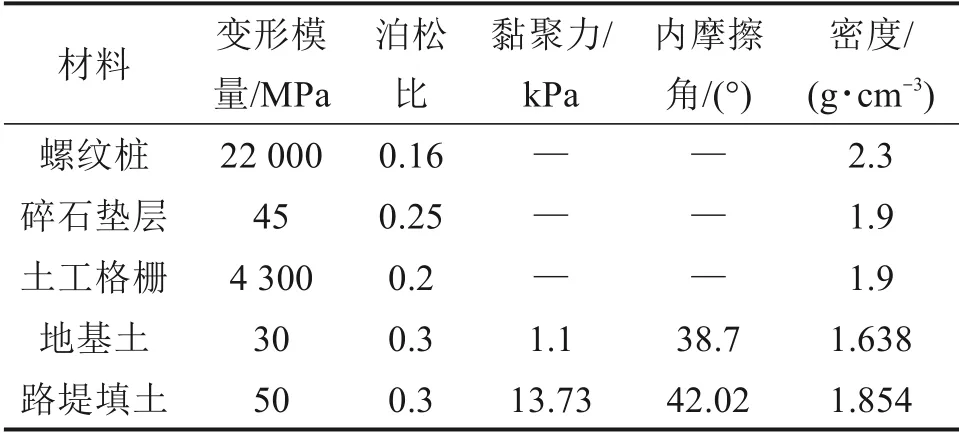
表1 有限元分析模型参数Table 1 Parameters for finite element analysis
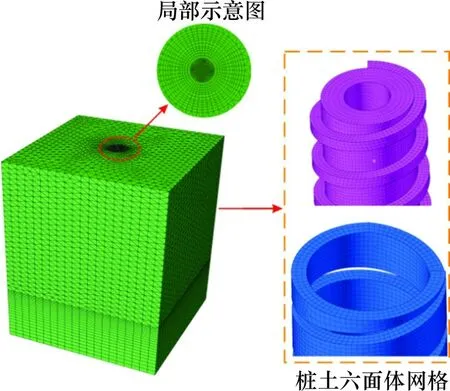
图7 螺纹桩网格划分Fig.7 Grid for screw pile and soil model
提取不同填土作用下的桩身轴力,如图8所示。
根据图8可知,桩身轴力沿桩身深度呈先增加后减小的变化趋势,存在明显的拐点,拐点所在位置即为中性点位置。填土高度0.6,1.2 与1.8 m条件下,中性点距桩顶中心距离分别为3.000,2.896与2.793 m,说明随着桩顶荷载的增加,中性点呈上升趋势。
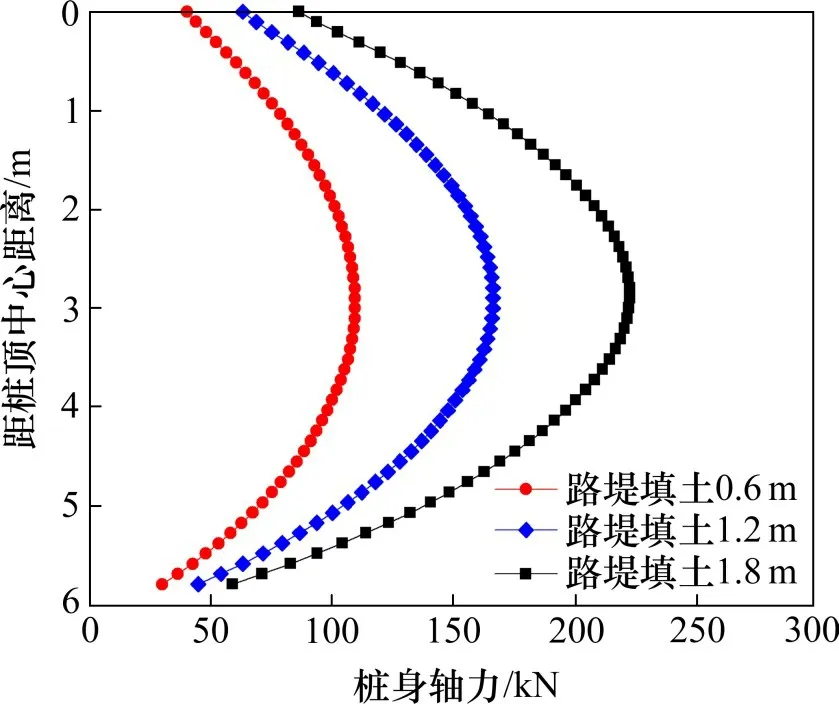
图8 桩身轴力分布曲线Fig.8 Curves of pile axial force
3.2 螺纹桩轴力计算方法数值验证
1) 参数的求解
螺纹桩基本参数如表2所示。

表2 螺纹桩基本参数Table 2 Basic parameters of screw piles
λ1表示桩侧土体发生屈服前的剪切位移刚度系数,kPa/mm;k1为螺纹下地基土发生屈服前后的压缩刚度系数;k3为桩端土发生屈服前后的压缩刚度系数,结合数值模拟分析,取k1=146.916 kPa/mm。
RANDOLPH 等[14]提出桩侧土体刚度系数计算如式(37)~(38)所示:
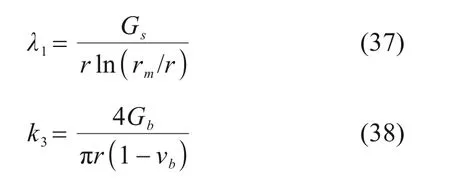
式中:Gs和Gb为桩侧、桩端土剪切模量,G=E/[2(1+υ)];rm为桩身影响半径;vb为桩端土的泊松比。
式中影响半径的计算式如(39)所示:
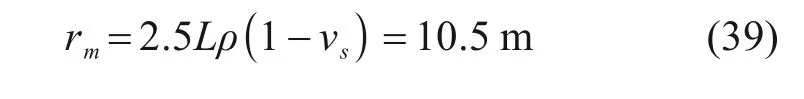
式中:vs为表示桩侧土体的泊松比;ρ为不均匀系数,ρ=G(0.5L)/G(L),表示桩入土深度1/2 处和桩端土的剪切模量之比。求解出λ1=14.570 kPa/mm;k3=104.940 kPa/mm。
以路堤填土高度0.6,1.2 与1.8 m 为例,由图10可知,此时桩顶荷载值分别为40.115,63.105与86.295 kN。绘制土体沉降沿桩身分布曲线如图9所示。
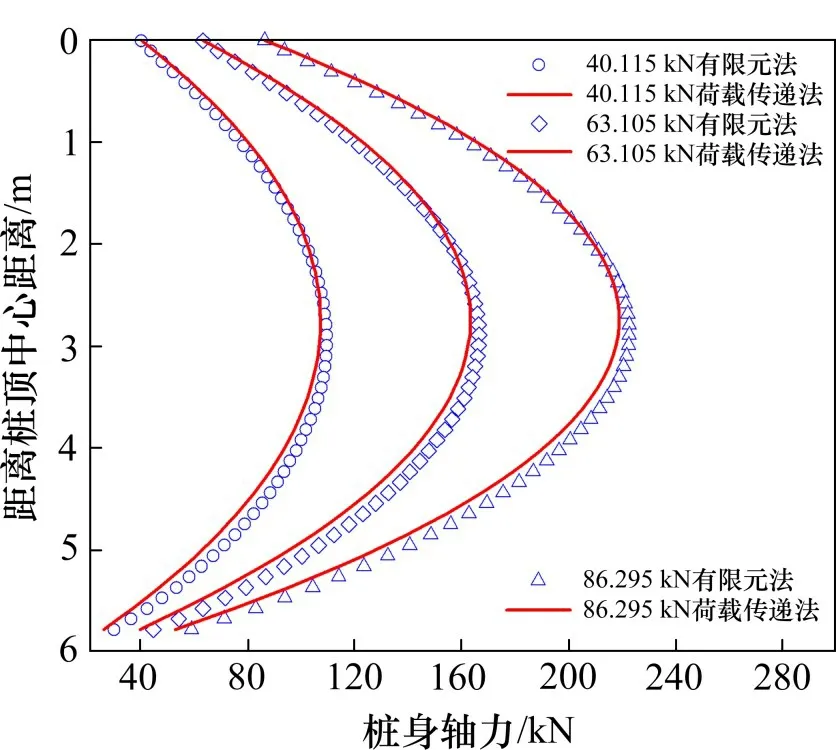
图10 荷载传递法计算结果与数值模拟比较Fig.10 Comparison between calculation results of load transfer method and numerical simulation
根据图9可知,计算桩周土体沉降斜率:
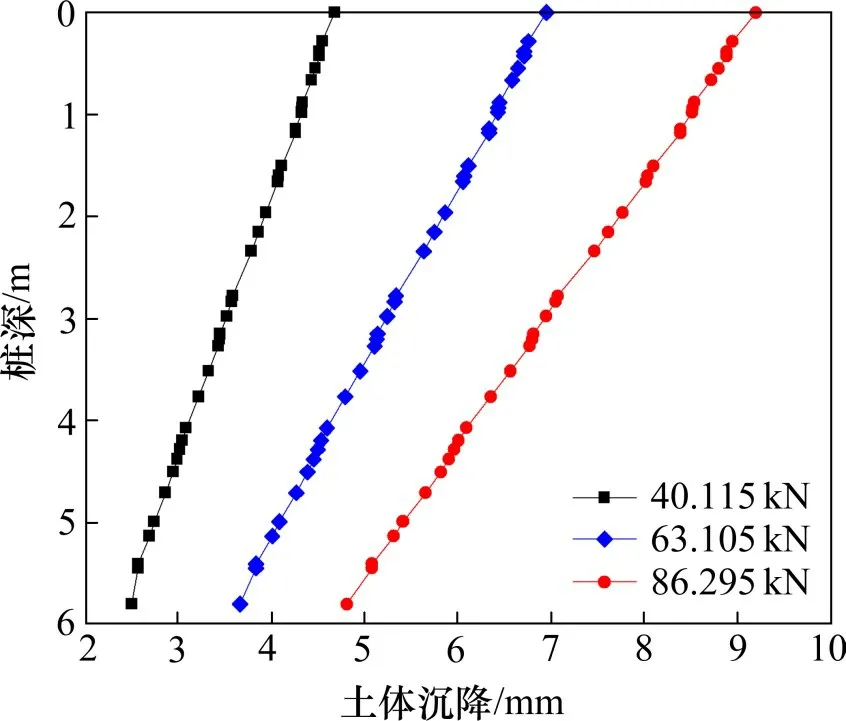
图9 土体沉降分布曲线Fig.9 Curves of soil settlement
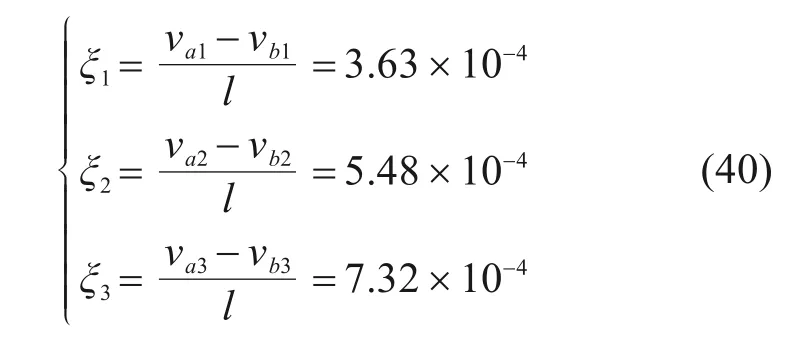
2) 待定系数的求解
在分析过程中,由于桩顶荷载较小,在进行有限元分析过程中,计算得到的桩土相对位移小于弹性变形极限值,在分析中按照螺纹桩桩侧与螺纹面处地基土处于弹性变形阶段的情况进行求解,由式(19)可知,当地基土处于弹性变形阶段时,桩土相对位移为u2(z)=C3sh(α1z)+C4ch(α1z),提取参数计算结果如表3所示。
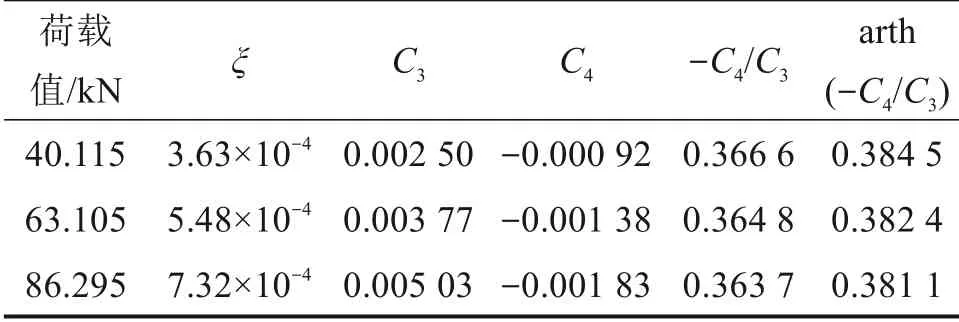
表3 不同荷载作用下待定系数Table 3 Undetermined coefficients under different loads
3) 中性点位置、桩身轴力与桩侧摩阻力
桩土相对位移用u(z)表示:
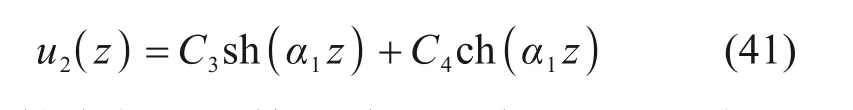
在中性点位置处桩土差异沉降u2(z)=0,求出中性点位置表达式:
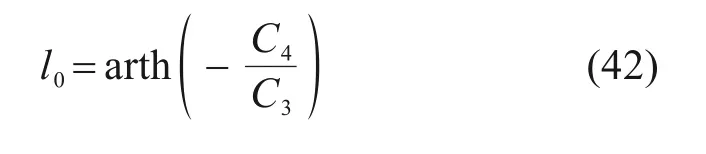
不同桩顶荷载下理论计算模型与有限元分析法得到的中性点位置如表4所示。
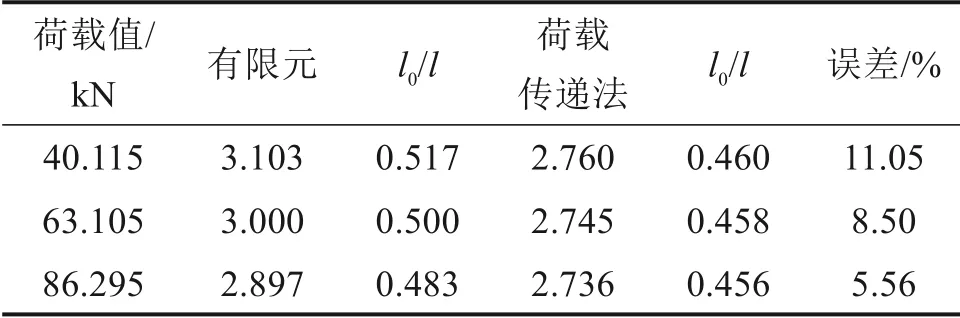
表4 中性点位置Table 4 Locating of neutral point
分析表4 可知,2 种方法得到的中性点位置误差最大不超过12%,中性点位置距桩顶0.455l~0.517l,随着荷载的增加,误差逐渐减小。同时可知,随着荷载的增大,中性点在桩身上的位置会有所上升,原因在于随着荷载的增加,桩侧土沿桩身向下的力也增大,使螺纹桩进一步下陷,导致中性点位置有所上升。
桩身轴力计算如式(43)所示:
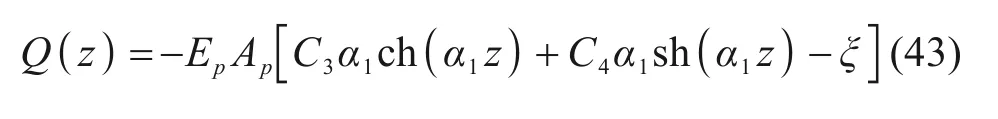
将不同荷载条件下利用有限元分析与荷载传递法计算得到的桩身轴力绘制在图10中。
根据图10 可知,通过荷载传递法与有限元分析法得到的桩身轴力在中性点位置以上较为吻合,在中性点以下,随着深度的增加,荷载传递法得到的桩身轴力衰减速度略快于有限元法计算结果。
计算在荷载40.115,63.105 与86.295 kN 情况下桩侧摩阻力分布曲线如图11所示。
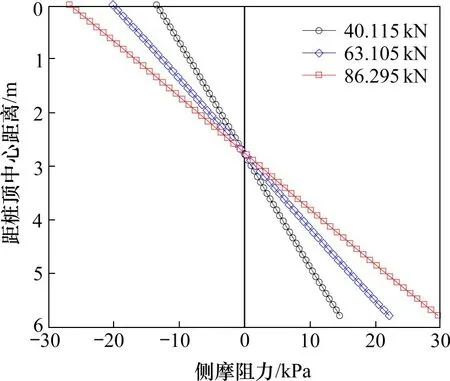
图11 桩身侧摩阻力变化曲线Fig.11 Distribution curves of pile shaft friction
4 结论
1) 在考虑桩侧负摩阻力影响的条件下,基于荷载传递法建立了填土荷载作用下螺纹桩复合地基单桩分析模型,该模型考虑了螺纹桩的受力特点,计算过程较为简单,概念明确。
2) 将荷载传递法得到的计算结果与三维有限元分析法得到的中性点位置相比较,中性点位置最大误差不超过12%,随着桩顶荷载的增加,误差逐渐减小,位置在0.455l~0.517l处。
3) 分析轴力沿桩身变化曲线可知,在中性点位置以上二者吻合较好,在中性点位置以下,有限元结果得到的轴力衰速度快于荷载传递法计算值。
