侧支撑长枕式减振轨道弹性垫板垂向刚度理论研究

张鹏，和振兴，石广田，白彦博

(兰州交通大学 机电工程学院，甘肃 兰州 730070)

弹性垫板是轨枕式减振轨道结构中的重要组成部件，其在增加轨道结构弹性、吸收振动能量和改善轮轨相互动力作用[1-2]等方面发挥着重要作用。对此，国内外学者对轨枕式减振轨道及弹性垫板进行了广泛的研究。CAⅠ等[3]建立车辆-有砟轨道-隧道空间耦合动力学模型，基于有限元法和车-轨相互作用动力学理论，分析了弹性长枕对车辆、轨道以及隧道动力响应的影响，并对枕下垫层合理刚度进行了探讨。尤瑞林等[4]在总结对比国内外标准的基础上，结合室内试验，对弹性轨枕枕下垫层静刚度的评估方法、试件的制作以及静刚度计算时荷载的取值范围3 个方面进行了优化。袁菁江等[5]通过建立车辆-减振型CRTSⅢ板式无砟轨道-桥梁耦合动力分析模型，探究了减振垫层的刚度取值范围。这些研究多是针对弹性垫板刚度对轨道结构动力学性能的影响，而从垫板的几何参数及受力状态分析垫板刚度的研究相对较少。KOH 等[6]将Haringx 柱模型[7]简化为仅包含剪切刚度与转动刚度的双弹簧模型，基于位移协调和受力平衡方程简化了弹性隔震支座的压缩特性，研究了轴向载荷对弹性支座动刚度、阻尼系数和高度折减的影响，为支座在轴向载荷作用下的响应分析[8-10]提供了依据。闫维明等[11]推导了不同剪切变形下弹性隔震支座拉伸刚度理论计算公式并进行验证，结果表明该文计算公式能够较好地分析弹性支座在小剪切变形下拉伸刚度的定量变化。孙新阳等[12-13]基于双弹簧模型和有效面积模型，研究了不同截面形状弹性支座在剪切变形下的压缩刚度，对比分析了不同支座的压缩性能。陈玉骥等[14]以拱形减振橡胶垫为对象，采用有限元法分析了半球形空腔半径、半径间距和橡胶垫厚度下橡胶垫的应力状态和极限承载力。和振兴[15]提出了一种新型的侧支撑无砟轨道结构，在该结构中侧支撑弹性垫板在施加于轨枕的载荷作用下会发生剪切和压缩组合变形，因此可以利用双弹簧模型模拟侧支撑弹性垫板的受力情况。在既有研究的基础上，本文基于侧支撑弹性垫板的双弹簧模型，推导了垫板垂向节点刚度的理论计算公式，研究了垫板关键几何参数对其节点刚度的影响，并建立不同垫板参数的轨道单元结构有限元模型进行了对比验证。

1 有限元模型的建立

1.1 侧支撑长枕式减振轨道结构

侧支撑长枕式减振轨道结构由道床、侧支撑弹性垫板和轨枕组成，轨枕嵌入道床预留的承轨槽内，轨枕侧面与道床承轨槽倾斜侧壁通过侧支撑弹性垫板紧密贴合。当车辆通过轨道结构时，振动能量部分被弹性垫板吸收，其余沿轨枕两侧传递并相互抵消，从而起到平衡横向动荷载的作用，降低轨道结构振动对周围环境的影响。轨枕底面和承轨槽底面之间预留了20 mm 的排水槽，方便积水排出，减缓垫板老化。按照轨下垫板的实际尺寸，在轨枕上表面截取间隔1 500 mm 的2块纵向150 mm，横向170 mm 的矩形面作为受力面。侧支撑长枕式减振轨道单元结构如图1所示。

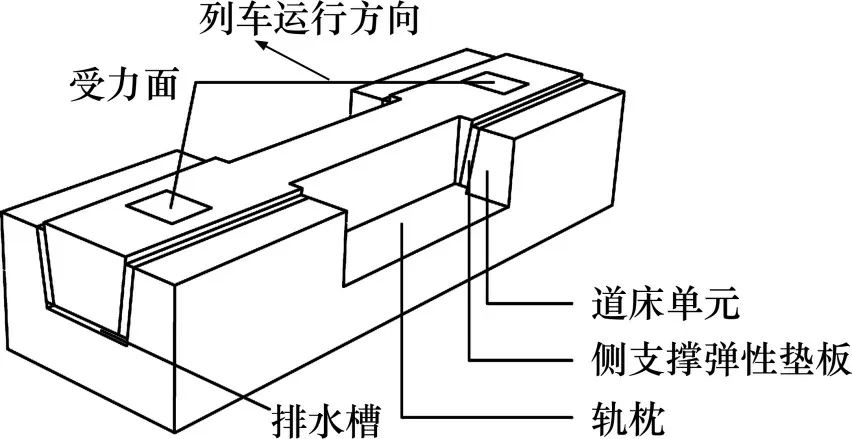
图1 侧支撑长枕式减振轨道单元结构Fig.1 Unit structure of theside-supported long sleeper vibration-damping track

垫板上表面两内侧边为一对对称的半径R=47 132 mm 的鼓形圆弧，中间位置宽度取324 mm，上下表面侧边的横向距离定义为空间倾斜量δ。在后续所有垫板参数变化过程中，均保持垫板上表面内侧边不动。侧支撑长枕式弹性垫板的结构示意图如图2所示。

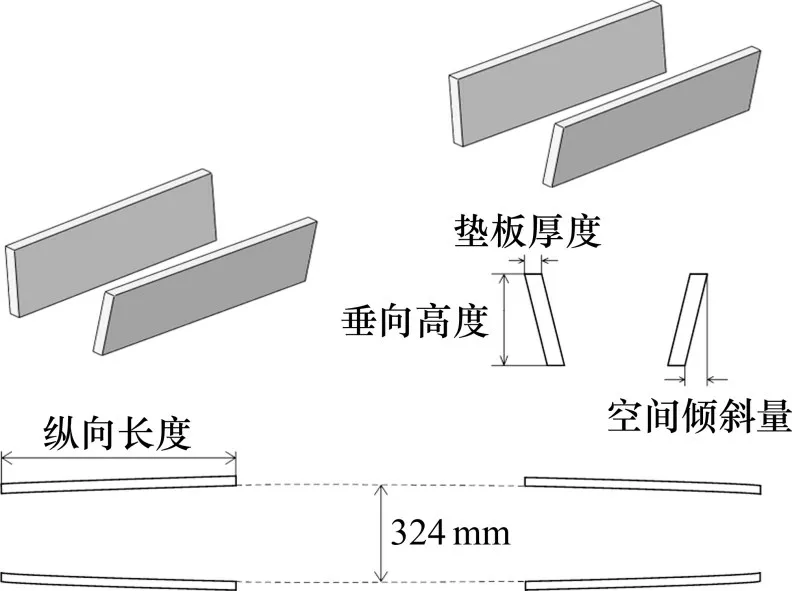
图2 垫板结构示意图Fig.2 Structural diagram of the elastic pads

轨枕长度为2 100 mm，横截面沿其纵向呈变截面等腰梯形状，可以限制轨枕的纵向位移。轨枕前后两侧面分别处于2个相交的圆锥面上，在现场更换时能够实现轨枕的自动对正。道床承轨槽两端贯通，可以减少道床宽度，降低工程造价。考虑到垫板厚度的变化，道床单元纵向长度取640 mm；横向长度与轨枕长度相等；承轨槽底面与道床底面距离为180 mm，道床整体高度随侧支撑弹性垫板的垂向高度而变化。

1.2 材料属性

以垫板厚度20 mm，空间倾斜量20 mm，纵向长度650 mm 和垂向高度200 mm 的模型为例，在1.1节所述2块受力面上分别施加40 kN的载荷，使轨枕产生3 mm 的垂向位移，在此基础上，取弹性垫板的杨氏模量为3×106Pa，泊松比为0.435，密度为1 700 kg/m3。轨枕材料选择C50混凝土，杨氏模 量 为3.45×1010Pa， 泊 松 比 为0.2， 密 度 为2 500 kg/m3；道床材料选择C40 混凝土，杨氏模量为3.25×1010Pa，泊松比为0.2，密度为2 440 kg/m3。并将3种材料的参数应用于后续计算。

1.3 有限元模拟过程

在实际轨道结构中，侧支撑弹性垫板与轨枕、道床之间通过摩擦接触相互连接，为了简化计算，有限元模拟时忽略垫板与轨枕、道床之间的摩擦，将轨枕侧面和垫板内侧、垫板外侧和承轨槽侧壁均采用绑定方式进行连接，并且根据结构自身的特点，只固定道床底面各节点的所有自由度。道床、轨枕和弹性垫板均采用八节点六面体单元进行网格划分，网格单元类型选择C3D8R。

依据GB/T 21527—2008《轨道交通扣件系统弹性垫板》[16]中弹性垫板静刚度的计算方法，在轨枕两端的受力面上分别施加100 kN 垂向载荷，加载时长为10 s。侧支撑长枕式减振轨道单元结构的有限元模型如图3所示。

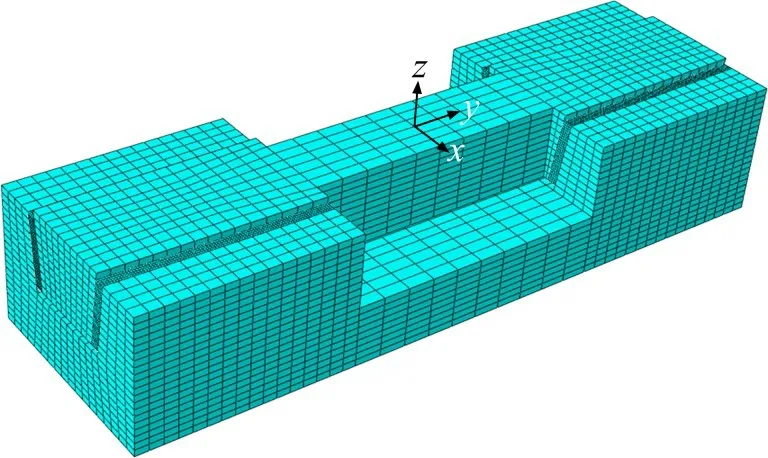
图3 有限元模型Fig.3 Finite element model

2 侧支撑弹性垫板双弹簧模型

2.1 双弹簧模型理论分析

结合侧支撑弹性垫板的实际结构，建立考虑垫板厚度、空间倾斜量、纵向长度和垂向高度等关键几何参数的双弹簧模型，如图4所示。模型中转动弹簧刚度为Kθ，剪切弹簧刚度为K，垫板厚度为l，空间倾斜量为δ，纵向长度为b，垂向高度为h，则垫板沿压缩方向的长度lC=lcosψ(ψ为垫板侧面与垂直方向的夹角，tanψ=δ h)，沿剪切方向的长度hG=h/cosψ。将分布于垫板的垂向载荷F0分解为沿垫板内侧面的剪切力F=F0cosψ和垂直于垫板内侧面的压缩力P=F0sinψ。

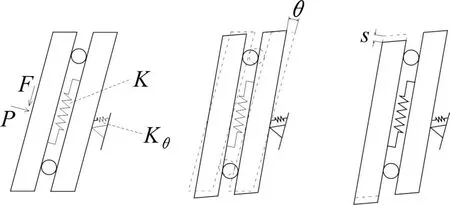
图4 双弹簧模型及其在剪切力作用下的变形Fig.4 Double spring model and its deformation under shear force

1) 剪切力的作用

在剪切力F的作用下，支座产生θ的转角，剪切弹簧变形为s，如图4 所示，则垫板内侧沿剪切方向的位移u和沿压缩方向的位移v可表示为：

由于支座的实际转角θ较小，式(1)和式(2)可转化为

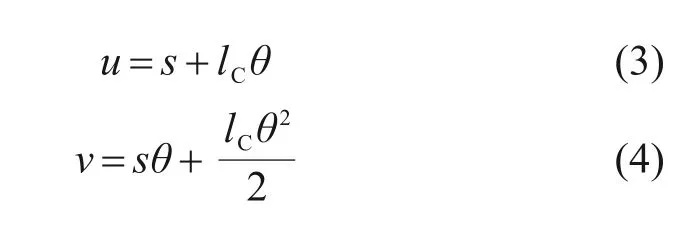
将上述方程中剪切与转动自由度解耦，考虑以下2种情况：

①若不考虑剪切变形，即假定K=∞，模型转化为带有转动弹簧约束的铰支刚性柱，此时转动弹簧的刚度如下式所示：

②若不考虑转动变形，即假定Kθ=∞，此时模型的剪切刚度为KlC，若已知垫板的杨氏模量为E，取剪切模量G=E3[17]，则模型的剪切刚度也可表示为GA(A为剪切面积)，则剪切弹簧的刚度如下式所示：

双弹簧模型在小转角时的平衡方程为：

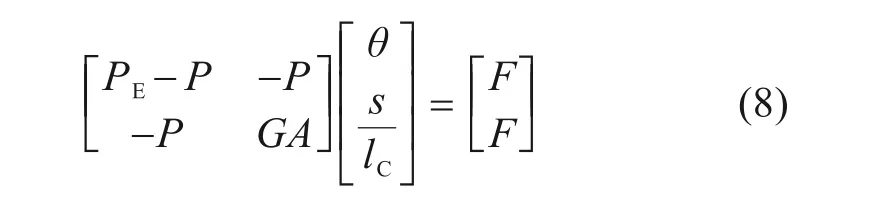
由式(8)可求得剪切弹簧变形s及转动弹簧转角θ，如下式所示：

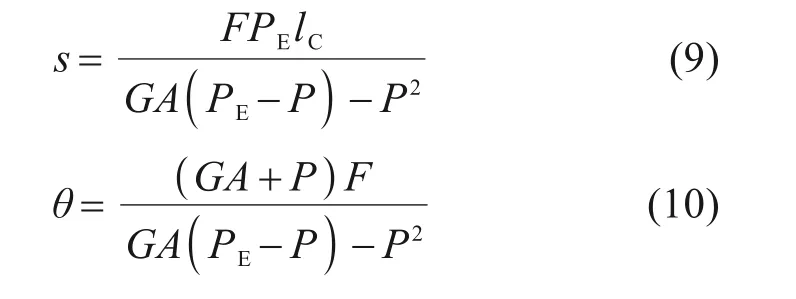
代入式(3)和式(4)中，可得剪切位移u和压缩位移v如下式所示：

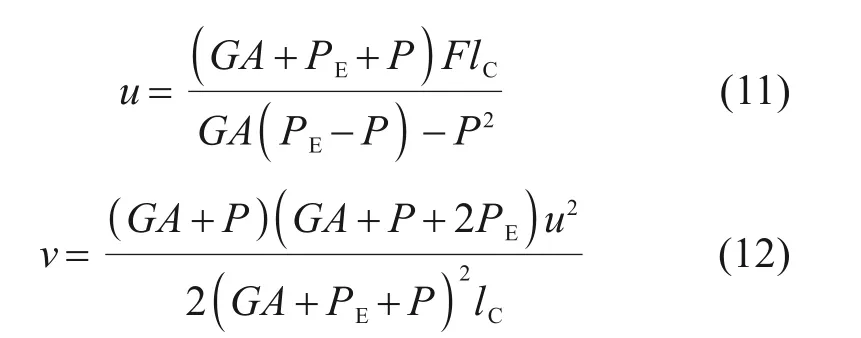
由于PE远大于GA及P，式(11)和式(12)可简化为

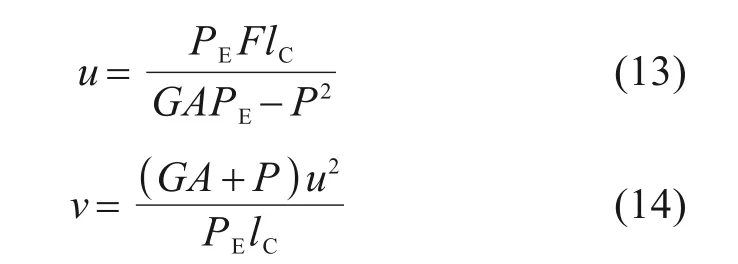
将式(5)和式(6)代入，得压缩位移v如下式所示：

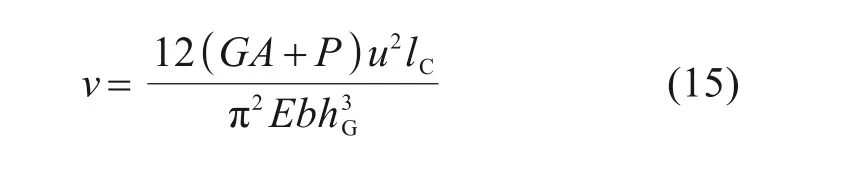
2) 压缩力的作用

在压缩力P的作用下，垫板内侧沿压缩方向的位移vC可表示为：

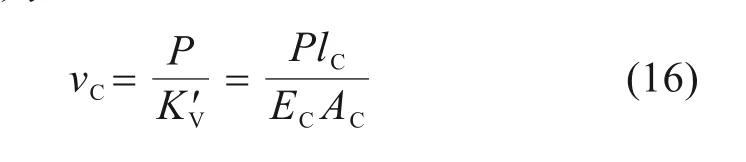
其中：K′V=ECAC/lC表示纯压缩状态下垫板的压缩刚度，EC=3E表示垫板的压缩模量，AC=b(hGlsinψ)表示有效受压面积。

则弹性垫板的总体压缩位移为：

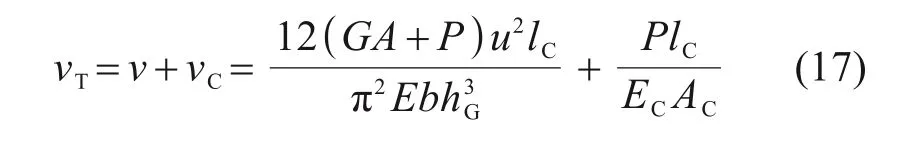
在剪切力F的作用下，弹性垫板的剪切刚度可表示为：

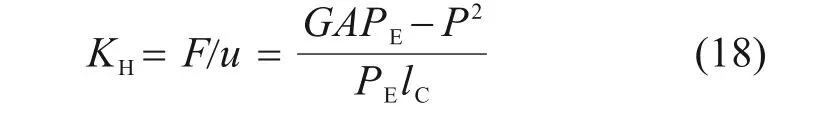
在压缩力P的作用下，弹性垫板的压缩刚度可表示为：

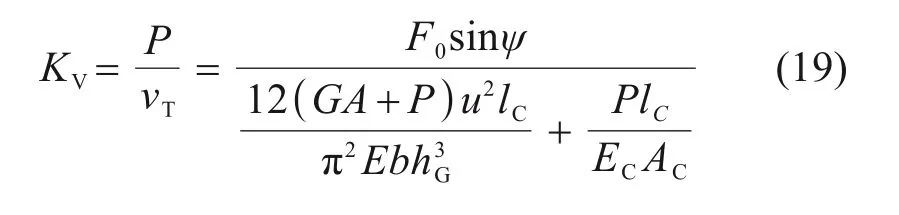
弹性垫板的垂向节点刚度K3与剪切刚度、压缩刚度之间的关系为：

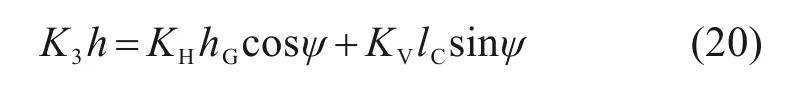
由以上推导可知，侧支撑弹性垫板的垂向节点刚度与垫板厚度、空间倾斜量、纵向长度和垂向高度有关。

2.2 垂向节点刚度有限元求解

文献[16]在计算弹性垫板的静刚度时，垂向载荷取100 kN，下限载荷与上限载荷分别取20 kN和80 kN。在侧支撑长枕式轨道结构中，由于结构的对称性，作用于轨枕一端的垂向载荷均匀地传递给两侧侧支撑弹性垫板，则单块垫板所受的垂向载荷是轨枕一端所受垂向载荷的一半即50 kN，相应地，计算单块垫板垂向节点刚度时下限载荷与上限载荷也随之减少一半。因轨枕侧面与垫板内侧采用绑定接触，轨枕垂向位移即为垫板内侧的垂向位移。则单块垫板的垂向节点刚度计算公式为

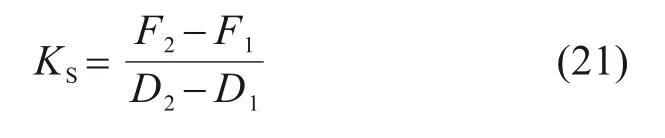
式中：上限载荷F2取40 kN，下限载荷F1取10 kN，D2为加载至上限载荷时垫板内侧的垂向位移，D1为加载至下限载荷时垫板内侧的垂向位移。

3 参数影响分析及对比验证

以侧支撑长枕式减振轨道的一个单元结构为研究对象，主要研究侧支撑弹性垫板的厚度、空间倾斜量、纵向长度和垂向高度的变化对其垂向节点刚度的影响规律。在研究某一参数的影响时，保持所有材料属性及另外3个参数不变，建立相应的有限元模型，通过有限元软件模拟轨道结构的垂向受压试验，根据式(21)计算出不同参数条件下侧支撑弹性垫板的垂向节点刚度，并与理论计算结果进行对比。

3.1 厚度的影响

保持垫板空间倾斜量(δ=20 mm)，纵向长度(b=650 mm)，垂向高度(h=200 mm)不变，分别建立垫板厚度为10，15，20，25 和30 mm 的实体模型。通过有限元模拟得到不同厚度条件下单块垫板的载荷-位移曲线，如图5 所示，计算出相应的垂向节点刚度，并与理论计算值进行对比，结果如表1所示。图6 为理论计算值与有限元模拟值对比曲线。

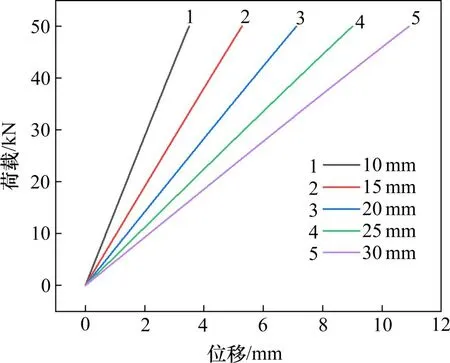
图5 不同厚度下弹性垫板的载荷-位移曲线Fig.5 Load-displacement curves of the elastic pad under different thicknesses

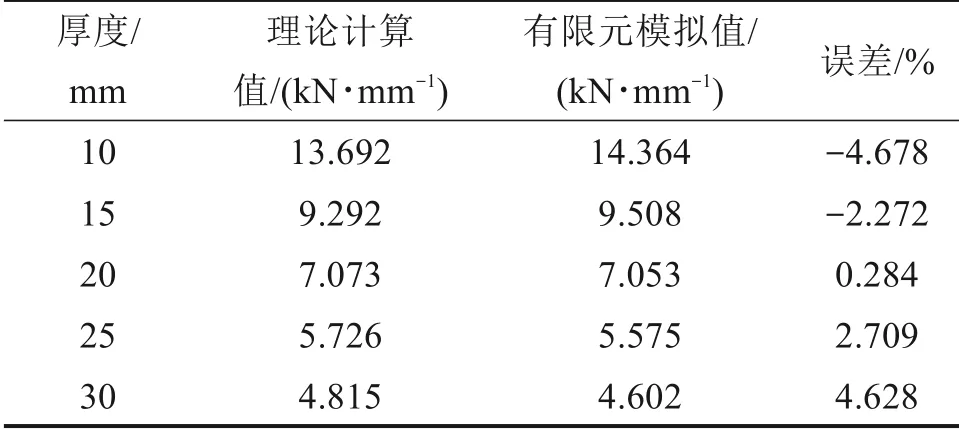
表1 不同厚度下弹性垫板垂向节点刚度对比Table 1 Comparison of vertical joint stiffness of the elastic pad under different thicknesses

图5表明，在施加于轨枕的垂向载荷不变的情况下，随着垫板厚度的增大，垫板的垂向位移随之增大。表1 表明，垫板厚度从10 mm 增大到30 mm时，垫板垂向节点刚度的理论计算结果与有限元分析结果吻合较好，相差在±5%以内。图6表明，随着垫板厚度的增大，垫板的垂向节点刚度随之减小，且垂向节点刚度与垫板厚度基本成反比例关系。

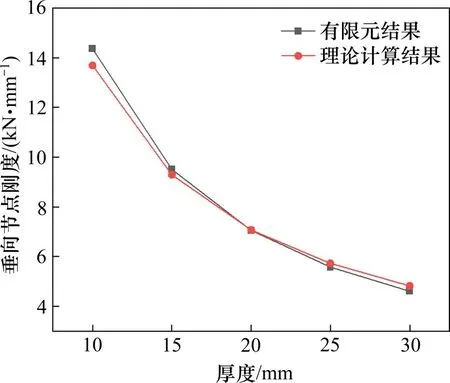
图6 厚度对垂向节点刚度的影响Fig.6 Ⅰnfluence of thicknesses on vertical joint stiffness

3.2 空间倾斜量的影响

保持垫板厚度(l=20 mm)，纵向长度(b=650 mm)和垂向高度(h=200 mm)不变，分别建立空间倾斜量δ从0 mm到32 mm以每4 mm增大的实体模型。通过有限元模拟得到不同空间倾斜量条件下单块垫板的载荷-位移曲线，如图7所示，计算出相应的垂向节点刚度，并与理论计算值进行对比，结果如表2 所示。图8 为理论计算值与有限元模拟值对比曲线。

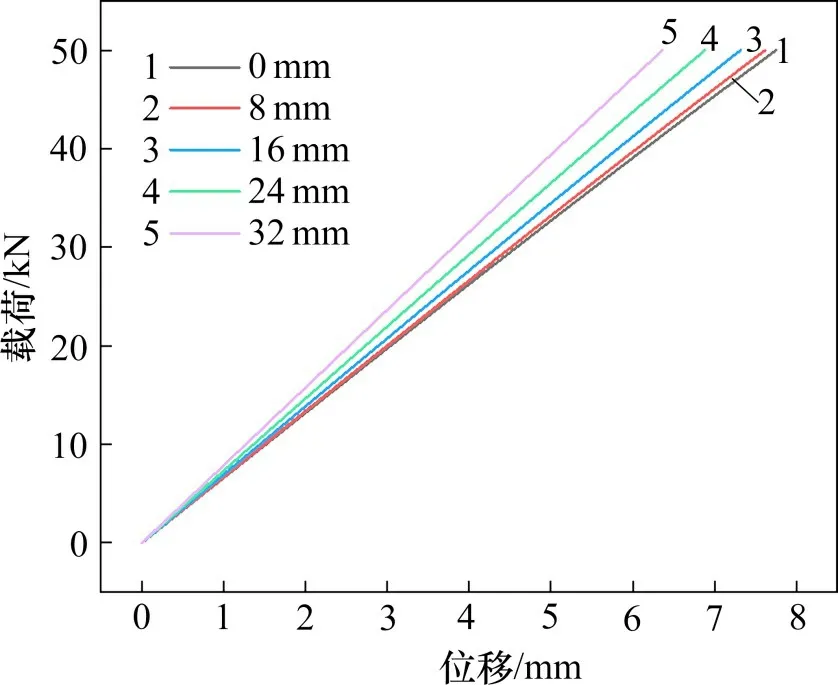
图7 不同空间倾斜量下弹性垫板的载荷-位移曲线Fig.7 Load-displacement curves of the elastic pad under different spatial inclinations

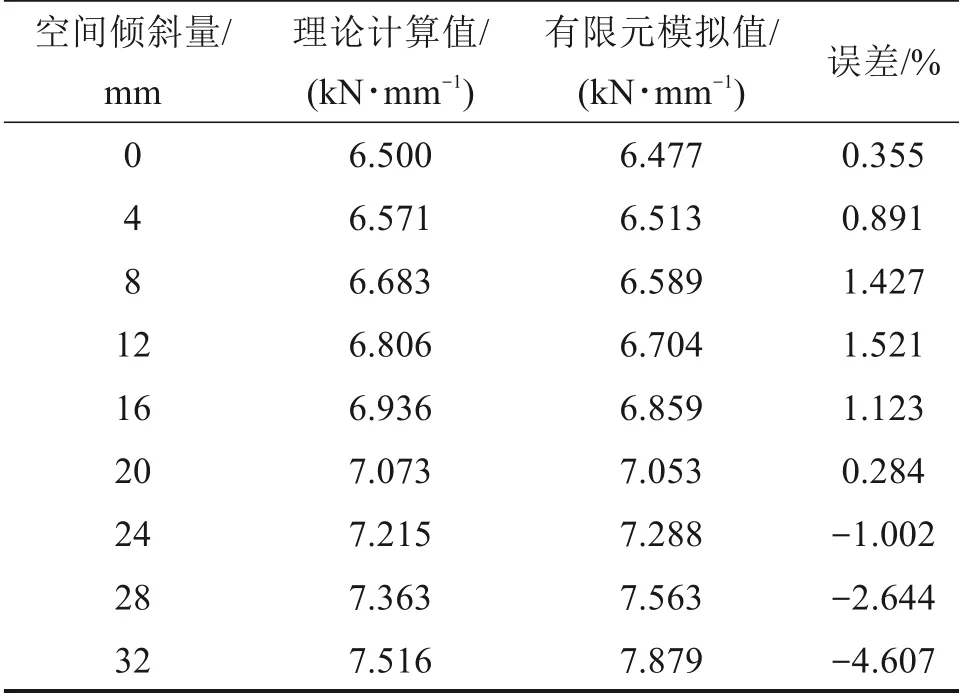
表2 不同空间倾斜量下弹性垫板垂向节点刚度对比Table 2 Comparison of vertical joint stiffness of the elastic pad under different spatial inclinations

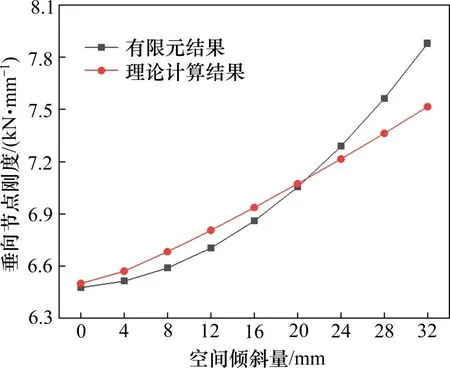
图8 空间倾斜量对垂向节点刚度的影响Fig.8 Ⅰnfluence of spatial inclinations on vertical joint stiffness

图7 表明，在施加于轨枕的垂向载荷不变的情况下，随着空间倾斜量的增大，垫板的垂向位移随之减小。表2 表明，空间倾斜量从0 mm 增大到32 mm时，垫板垂向节点刚度的理论计算结果与有限元分析结果吻合较好，相差均在±5%以内。图8表明，随着空间倾斜量的增大，垫板的垂向节点刚度随之增大。这是因为随着空间倾斜量的增大，垫板所受的剪切力不断减小而压缩力不断增大，由于材料的剪切模量远小于压缩模量，垫板内侧的垂向位移减小，垫板的垂向节点刚度增大。

3.3 纵向长度的影响

持垫板厚度(l=20 mm)，空间倾斜量(δ=20 mm)和垫板垂向高度(h=200 mm)不变，分别建立垫板纵向长度为600，650，700 和750 mm 的实体模型。通过有限元模拟得到不同纵向长度条件下单块垫板的载荷-位移曲线，如图9所示，计算出相应的垂向节点刚度，并与理论计算值进行对比，结果如表3 所示。图10 为理论计算值与有限元模拟值对比曲线。

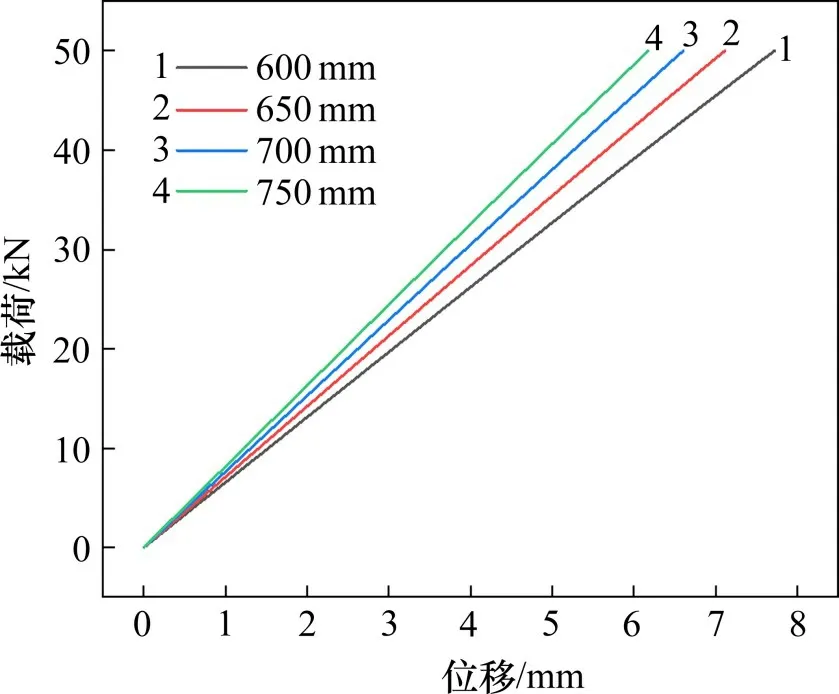
图9 不同纵向长度下弹性垫板的载荷-位移曲线Fig.9 Load-displacement curves of the elastic pad under different longitudinal lengths

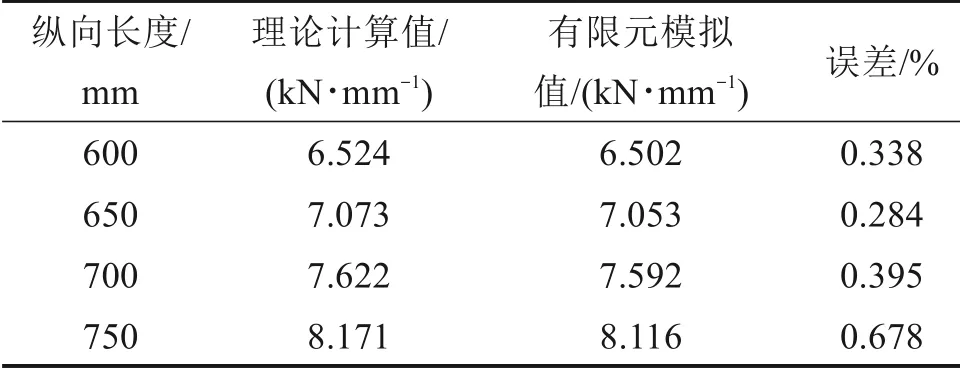
表3 不同纵向长度下弹性垫板垂向节点刚度对比Table 3 Comparison of vertical joint stiffness of the elastic pad under different longitudinal lengths

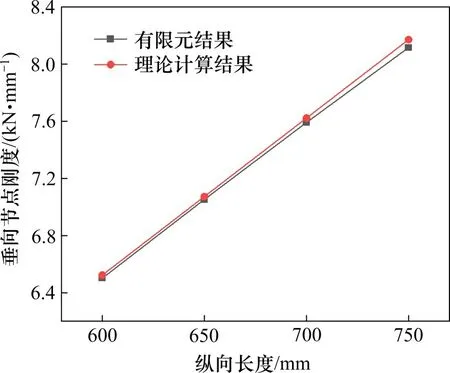
图10 纵向长度对垂向节点刚度的影响Fig.10 Ⅰnfluence of longitudinal lengths on vertical joint stiffness

图9 表明，在施加于轨枕的垂向载荷不变的情况下，随着纵向长度的增大，垫板的垂向位移随之减小。表3 表明，纵向长度从600 mm 增大到750 mm 时，垫板垂向节点刚度的理论计算结果与有限元分析结果吻合较好，相差均在±5%以内。图10 表明，随着纵向长度的增大，垫板的垂向节点刚度随之增大。这是因为随着纵向长度的增大，垫板的受力面积增大，垂向节点刚度随之减小。

3.4 垂向高度的影响

保持垫板厚度(l=20 mm)，空间倾斜量(δ=20 mm)和垫板纵向长度(b=650 mm)不变，分别建立垫板垂向高度为150，200，250 和300 mm 的实体模型。通过有限元模拟得到不同垂向高度条件下单块垫板的载荷-位移曲线，如图11 所示，计算出相应的垂向节点刚度，并与理论计算值进行对比，结果如表4 所示。图12 为理论计算值与有限元模拟值对比曲线。

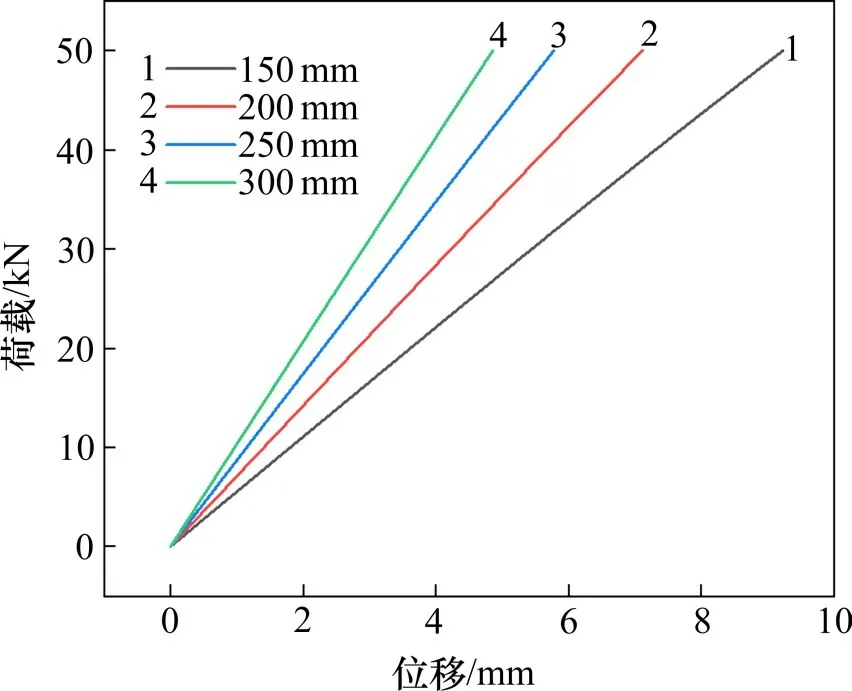
图11 不同垂向高度下弹性垫板的载荷-位移曲线Fig.11 Load-displacement curves of theelastic pad under different vertical heights

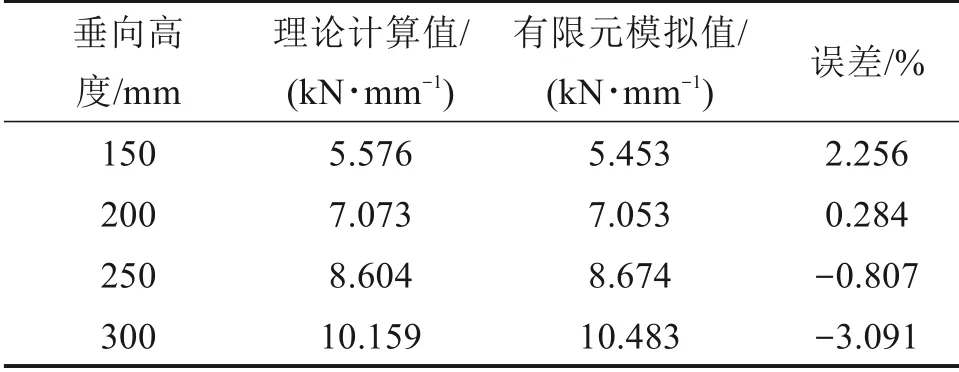
表4 不同垂向高度下弹性垫板垂向节点刚度对比Table 4 Comparison of vertical joint stiffness of the elastic pad under different vertical heights

图11 表明，在施加于轨枕的垂向载荷不变的情况下，随着垂向高度的增大，垫板的垂向位移随之减小。表4 表明，垂向高度从150 mm 增大到300 mm 时，垫板垂向节点刚度的理论计算结果与有限元分析结果吻合较好，相差均在±5%以内。图12 表明，随着垂向高度的增大，垫板的垂向节点刚度随之增大，同样是因为垫板受力面积增大的原因。

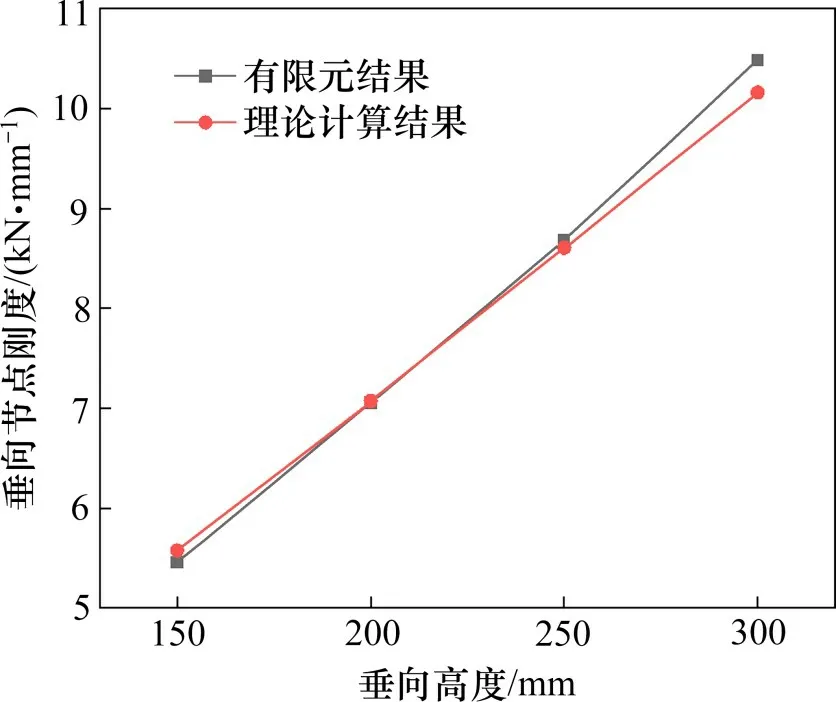
图12 垂向高度对垂向节点刚度的影响Fig.12 Ⅰnfluence of vertical heights on vertical joint stiffness

4 结论

1) 通过与有限元模拟结果对比，本文建立的综合考虑侧支撑弹性垫板关键几何参数的双弹簧模型能够准确模拟侧支撑弹性垫板在不同压剪组合作用下的受力状态及变形情况。

2) 侧支撑弹性垫板的垂向节点刚度与垫板的厚度、空间倾斜量、纵向长度和垂向高度有关，其值随垫板厚度的增大而减小，且垂向节点刚度与垫板厚度基本成反比例关系；随空间倾斜量、纵向长度和垂向高度的增大而增大。

3) 当侧支撑弹性垫板相关几何参数变化时，其垂向节点刚度的理论计算值与有限元模拟值吻合较好，相差均在±5%以内，表明可以通过改变侧支撑弹性垫板的几何参数调整其压剪受力状态，改变垫板的传力特性，获得工程需要的节点垂向刚度。这对提高新型侧支撑长枕式减振轨道的开发效率，适应不同的减振需求具有理论指导意义。