Decision-Making Models Based on Meta-Reinforcement Learning for Intelligent Vehicles at Urban Intersections

Xuemei Chen, Jiahe Liu, Zijia Wang, Xintong Han, Yufan Sun, Xuelong Zheng

Abstract: Behavioral decision-making at urban intersections is one of the primary difficulties currently impeding the development of intelligent vehicle technology. The problem is that existing decision-making algorithms cannot effectively deal with complex random scenarios at urban intersections. To deal with this, a deep deterministic policy gradient (DDPG) decision-making algorithm (T-DDPG) based on a time-series Markov decision process (T-MDP) was developed, where the state was extended to collect observations from several consecutive frames. Experiments found that T-DDPG performed better in terms of convergence and generalizability in complex intersection scenarios than a traditional DDPG algorithm. Furthermore, model-agnostic meta-learning(MAML) was incorporated into the T-DDPG algorithm to improve the training method, leading to a decision algorithm (T-MAML-DDPG) based on a secondary gradient. Simulation experiments of intersection scenarios were carried out on the Gym-Carla platform to verify and compare the decision models. The results showed that T-MAML-DDPG was able to easily deal with the random states of complex intersection scenarios, which could improve traffic safety and efficiency. The above decision-making models based on meta-reinforcement learning are significant for enhancing the decision-making ability of intelligent vehicles at urban intersections.

Keywords: decision-making; intelligent vehicles; meta learning; reinforcement learning; urban intersections

1 Introduction

A safe and efficient decision-making model is critical to the development of intelligent vehicles and is a key factor that will ultimately enable intelligent vehicles to drive autonomously on complex roads. However, current decision-making algorithms for intelligent vehicles are far from mature enough to effectively cope with various dynamic and complex traffic scenarios. Therefore, for improving safety, efficiency, environmental adaptability, etc., the behavioral decision-making of intelligent vehicles is of great research significance.

In recent years, scholars from all over the world have conducted extensive research on behavioral decision-making models of intelligent vehicles. These methods can be divided into three types: models based on rules, utility value, and machine learning. The “BOSS” team at Carnegie Mellon University [1], the “Junior” team at Stanford University [2], the “Annie Way” team at MIT [3], etc., have all adopted rule-based decision-making algorithms. Through the real-time construction of predetermined knowledge and rules related to driving behavior, a series of manually defined decision states can be realized to make accurate behavioral decisions [4]. The AnnieWAY intelligent vehicle team at the Karlsruhe University of Technology [5] established a parallel hierarchical state machine to build a decision-making system to respond to various situations in the environment. The mobile navigation distributed architecture proposed by the Braunschweig University of Technology [6]includes a series of driving behaviors (path following, lane keeping, obstacle avoidance, driving in parking areas, etc.). Driving behaviors are decided by a voting mechanism and applied to the Caroline intelligent vehicle [7]. To deal with the problem of vehicles merging, Chen et al. [8]proposed merging strategies based on the leastsquares policy iteration (LSPI) algorithm, which selected basis functions including the reciprocal TTC, relative distance, and relative speed to represent the state space and discretize the action space.

These rule-based decision-making systems have the advantages of explicit execution and simple realization but ignore the complexity and uncertainty of dynamic traffic factors at intersections. Compared with human drivers, these systems are too conservative and not flexible enough to deal with decision-making tasks in intersection scenarios with both manned and unmanned vehicles. Therefore, rule-based behavioral decision-making methods have weak generalizability and poor adaptability. On the other hand, utility-value-based decision-making models select an optimal driving strategy/action among multiple alternatives according to the maximum utility theory. The utility value function is defined during the selection of decision-making schemes [9].For the behavioral decision-making of intelligent vehicles, the quality of driving strategy is quantitatively evaluated through multiple criteria, such as driving safety, efficiency, and comfort. Bahram et al. [10] proposed a driving strategy selection mechanism that predicted future responses.Through the prediction of future driving scenarios, the quality of the driving strategy was quantitatively evaluated according to multiple goals such as driving safety, traffic rules, and driving comfort. The real-time optimal strategy was verified in a simulation environment. Furda A et al.[11] used a multi-criteria decision-making method to select 11 criteria to calculate utility values,obtained the action utility table of the driving actions, and then determined the optimal driving action from a set of candidate actions. Nagi et al. [12] established a multi-objective overtaking behavior model based on the Q learning algorithm, and by using the weighted addition of the utility values of multiple criteria, they obtained the final Q value (action-utility value) for decision-making.

These utility value models make reasonable decisions for different driving scenarios and have certain environmental adaptability. However,most of them are only based on driving safety requirements, and the decision-making process does not consider the information interactions with the environment, which limits their application in urban intersections. Finally, progress in machine learning (ML) has made it possible for end-to-end autonomous driving methods based solely on ML to exist. There are two main approaches: imitation learning (IL) and reinforcement learning (RL). For example, Bojarski et al. [13] used Convolutional neural networks(CNNs) to perform imitation learning of decision-making and control a vehicle based on the original image information of its visual sensors and tested it in structured and unstructured road scenarios. Codevilla et al. [14] proposed a conditional imitation learning method, which accelerated imitation learning by introducing human driver instructions and allowed the driver to intervene in decision-making to a certain extent to ensure driving safety. Kuefler et al. [15] used generative adversarial networks (GAN) to imitate expert drivers to make decisions. Experiments demonstrated that this method was able to learn high-level strategies such as emergency handling. However, it requires massive data support and has disadvantages such as high model training costs, inability to adjust and optimize strategies online according to environmental changes, and difficulty in adapting to a complex and shifting real road environment. Reinforcement learning can learn to optimize strategies through the process of online interaction with the environment. In recent years, reinforcement learning has prevailed remarkably in robot control [16] and advanced driving assistance systems [17] and has been applied in intelligent vehicle behavioral decision-making. Mirchevska et al.[18] used the deep Q network (DQN) method to make intelligent vehicle lane change behavior decisions in highway scenarios. Simulation experiments found that the decision-making performance of this method was better than traditional methods based on human-defined rules.Wang et al. [19] used continuous states and action spaces to design a Q function approximator with a closed greedy strategy to improve the computational efficiency of the deep Q network,and then to learn faster and obtain a smooth and effective lane changing strategy. However,because reinforcement learning methods do not use prior knowledge and only seek optimal strategies through active strategy exploration, their learning efficiency is low, and their ability to deal with complex problems is insufficient, which restricts their application in intelligent vehicles decision-making at urban intersections.

In summary, existing decision-making algorithms have weak generalizability for various dynamic and complex environments and cannot effectively deal with random scenarios of urban intersections. Therefore, in response to the above problems, a deep deterministic policy gradient(DDPG) decision algorithm (T-DDPG) based on a time-series Markov decision process was developed, and the idea of model-agnostic metalearning (MAML) was integrated into the TDDPG algorithm so that the decision algorithm(T-MAML-DDPG) was able to adapt to the random states of complex intersection scenarios and achieve better generalizability. The decision-making models proposed in this paper have a certain significance for improving the generalization and adaptability of intelligent vehicle decision-making at urban intersections, thus improving traffic safety and efficiency.

The structure of this paper is as follows: Section 2 discusses the methods involved in the research, including the DDPG and the MAML methods, while Section 3 defines the models established in this paper. Section 4 elaborates on the simulation experiments and analysis results.The effects of the decision models were verified using the Gym-Carla simulation platform. Section 5 presents the conclusions of this paper and prospects for future work.

2 Methodology

2.1 Deep Deterministic Policy Gradient (DDPG)

The problem to be solved by reinforcement learning can be abstracted into a Markov decision process (MDP). The characteristic of an MDP is that the state of the system at the next moment is determined by the state at the current moment and has no connection with earlier moments.

DDPG is an improved Actor-Critic method.In the Actor-Critic algorithm, the policy function in the Actor outputs an action according to a given current state. The Critic evaluates the action value function based on the output value of the Actor and the current state. The evaluation policy is updated according to temporal-difference learning, and the Actor policy is updated according to the policy gradient [20]. The policy in the DDPG algorithm is not stochastic, but deterministic. This means that the network of the Actor outputs only real actions, rather than probabilities of different actions.

2.2 Model-Agnostic Meta-Learning (MAML)

In meta-learning, the goal of training the model is to quickly learn to accomplish various new tasks from a small amount of new data. The key idea of this method is to train the initial parameters of the model to ensure that after the parameters are updated through several gradient steps,the model has the greatest performance for the new tasks. These gradient update steps are calculated from a small amount of data from the new task.

3 Models

3.1 T-DDPG Model

3.2 T-MAML-DDPG Model

The generalization performance of a decisionmaking algorithm in an urban intersection environment refers to: 1) Its performance across multiple intersections. For example, if an algorithm converges for intersection A, its performance can be tested at intersections B and C. 2) Its performance when facing different situations at the same intersection, such as different number of vehicles and motion states in the intersection. To improve the adaptability of the decision-making algorithm at the same complex intersection, an MAML-based T-DDPG decision algorithm (TMAML-DDPG) was proposed.

For the ego vehicle agent, at each interaction episode, the random initial positions of the environmental vehicles and the random and changeable motion states were new tasks. Adapting and learning an appropriate policy in a scenario full of new tasks was the issue that needed resolving.

Incorporating the ideas of MAML into the deep reinforcement learning T-DDPG, the new approach enabled the intelligent vehicle agent to use a small amount of experience acquired through interaction with the environment to quickly obtain a policy for each new scenario task. A new task may include achieving a new goal or a previously trained goal in a new environment. For example, an intelligent vehicle agent could learn to deal with a task scenario with 4 environmental vehicles through training and quickly adapt when facing the next training scenario with 5 environmental vehicles.

For T-DDPG, the most important target was to quickly adapt the Actor network to new tasks. Therefore, based on the idea of MAML,the Actor network was designed with a secondary gradient, so that the policy could quickly adapt to complex and changeable scenarios. For the application of T-MAML-DDPG, the meta objective function is the gradient of the Actor network. The sum of the gradients of the Actor network in each new task was calculated by sampling the new task data set, and the total gradient was updated. The algorithm is as follows:

Step 1 Set the scenario and environmental vehicles, and train n random scenarios.

Step 2 The exploration network outputs random actionaaccording to the current environment observation states.

Step 3 The agent performs actiona, and the reward function returns the real-time reward valueR.

Step 4 The agent obtains the observation states′at the next moment.

Step 5 The experience data〈s,a,r,s′〉is inserted into the experience pool.

Step 6 The Critic network is updated based on the experience pool data.

4 Experiments

4.1 Comparison and Verification of T-DDPG and DDPG Decision Models

To verify this new model, urban intersection scenarios were set up in Carla, and the generalizability of the T-DDPG model was tested in complex random scenarios. The left-turn path was fixed in the intersection scene where the left-turn and straight-through shared signal lights, and the expected speed in the reward function was set to 15 km/h based on normal driving data.

To ensure the diversity and randomness of the scenarios in each training episode, the number of environmental vehicles was set to 3−5, the initial positions were random, and the environmental vehicles were set to autopilot mode in Carla. In autopilot mode, the oncoming environmental vehicles moved randomly, possibly turning left, going straight, or turning right, and their speed also changed randomly. Moreover,the intelligent ego vehicle was able to interact with the environmental vehicles, meaning that the motion states of the ego vehicle affected the motion states of the environmental vehicles. If most of the body of the ego vehicle has traveled in front of the environmental vehicle during a left turn, the environmental vehicle would adopt a deceleration strategy.

DDPG and T-DDPG were trained in random and complex scenarios respectively. The DDPG here is an ordinary implementation serving as the baseline. Whenever a collision occurred or when the ego vehicle agent crossed the intersection and reached the target lane, the current episode was ended, and a new episode was started. 1 test was performed after every 20 episodes of training. Fig. 1 shows the test results of DDPG and T-DDPG. The abscissa is the number of tests, and the ordinate is the sum of the reward values of each frame of the episode.The decision model based on DDPG still oscillated violently after 120 tests, with no trend of convergence. The T-DDPG-based decision-making model basically converged after 80 tests, and the total reward value was approximately 0,which shows that the model was able to find an ideal policy in a random and complex environment.

The DDPG and T-DDPG models, after 2000 episodes of training, were put into 100 random scenarios for testing, and the numbers of times the 2 models successfully crossed the intersection were compared. As shown in Tab. 1, the pass rate of the DDPG model was 49%, and the pass rate of the T-DDPG model was 92%, which shows that compared to the DDPG model, the pass rate of T-DDPG had an improvement of 83.7%.

4.2 Verification of the T-DDPG Model at Virtual Urban Intersections

Fig. 1 Models test results: (a)DDPG; (b)T-DDPG

Tab. 1 Comparison of the success rate of the 2 models

Next up, the generalization performance of the T-DDPG decision model was tested in complex random scenarios to verify its ability to select policies taking both security and efficiency into consideration. The environmental vehicles were once again set to autopilot mode in Carla. This mode simulates the driving habits of human drivers. The motion states of the ego vehicle affected the motion of environmental vehicles,meaning that the decision-making model considered interactions with environmental vehicles.The T-DDPG model, after 2000 episodes of training, was tested in random scenario. The test results are as follows:

Scenario 1 There were 3 environmental vehicles. The ego vehicle focused on efficiency and tended to go first. In this scenario, the 3 environmental vehicles were in the same lane. The ego vehicle adopted the rush strategy after vehicle 1 turned left. Fig. 2(b) depicts the speed changes of each vehicle. In the first 3.5 s, each vehicle accelerated forward, and the ego vehicle kept accelerating and passed the conflict zone first. At this time, vehicle 2 decelerated to yield and waited for the ego vehicle to pass the conflict zone, before speeding up and moving forward.Vehicle 3 basically maintained its speed in the rear. Fig. 2(c) describes the output policy of the decision-making model in this scenario, with the acceleration curve rising rapidly at first and then slowing down.tended to go first. Vehicle 1 turned right, but its route did not affect the left-turn route of the ego vehicle. The ego vehicle chose to accelerate first,pass the conflict zone before vehicles 2, 3, and 4 reached it, and arrived at the target lane.Fig. 3(b) describes the speeds changes of each vehicle. Vehicle 2 accelerated first, while vehicle 4 was slower, and only accelerated to 6 m/s after

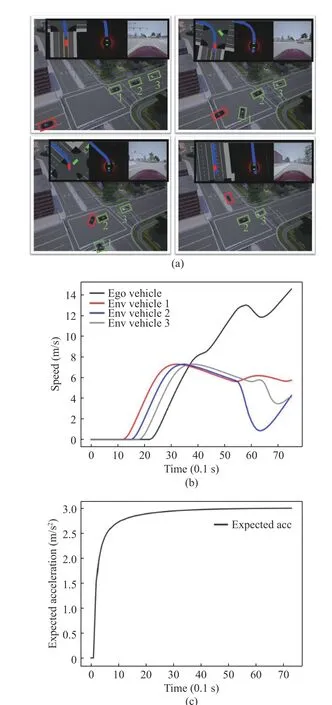
Fig. 2 Scenario 1 test results: (a)Gym-carla scenario 1;(b)speeds of vehicles; (c)longitudinal expected acceleration

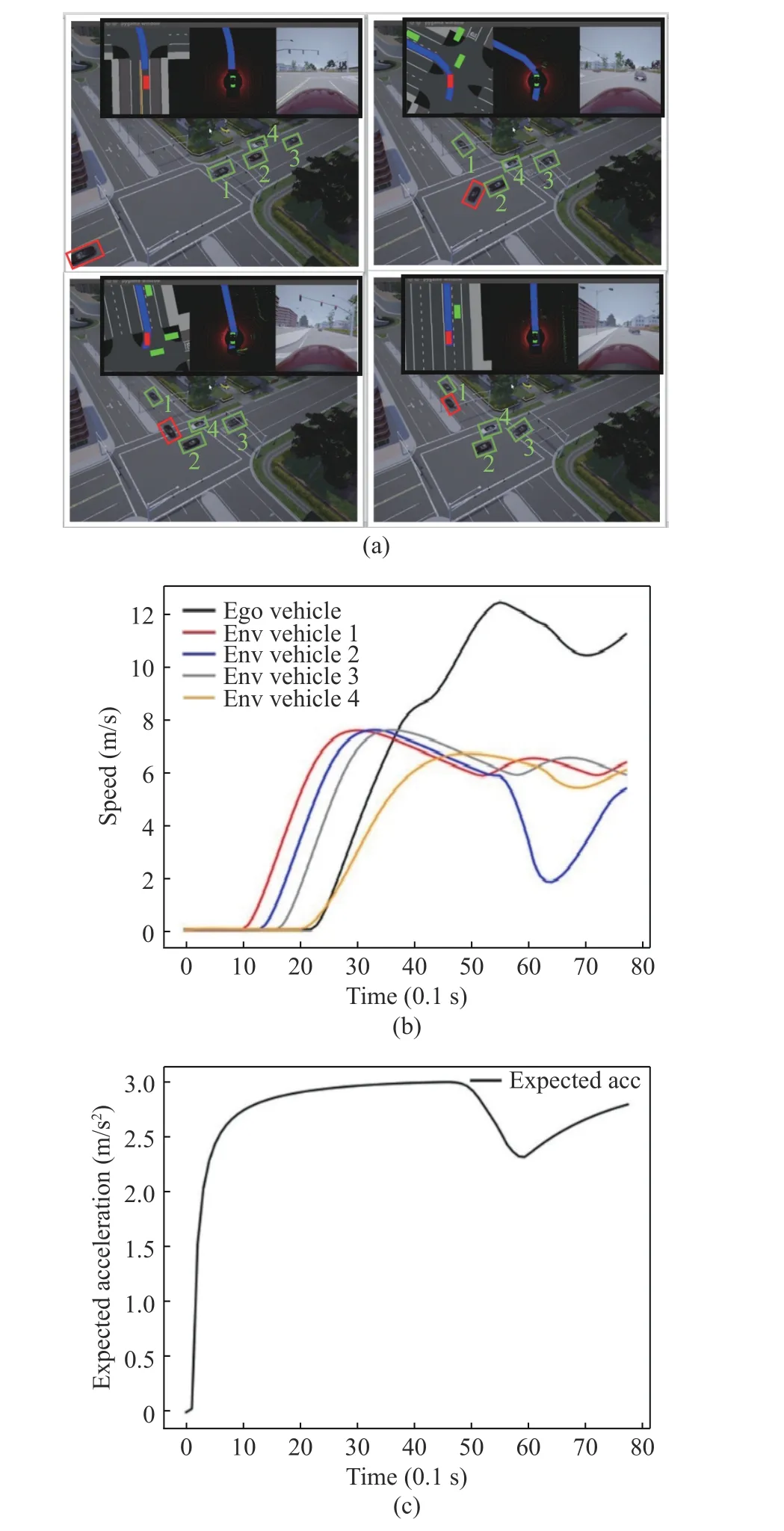
Fig. 3 Scenario 2 test results: (a)Gym-carla scenario 2;(b)speeds of vehicles; (c)longitudinal expected acceleration

Scenario 2 There were 4 environmental vehicles. The ego vehicle focused on efficiency and 4 s. The ego vehicle chose to go first according to the positions and speeds of the environmental vehicles, kept accelerating, and drove to the target lane through the conflict zone first. Vehicle 2 decelerated at 5.5 s because of the ego vehicle’s acceleration strategy, and then accelerated forward. Vehicles 4 and 3 were far away from the conflict zone, and maintained their speed throughout the scenario.

Scenario 3 There were 5 environmental vehicles. The ego vehicle focused on efficiency and tended to go first. Vehicle 1 turned left. As can be seen from Fig. 4(a), vehicles 4 and 5 accelerated, while vehicle 2 wanted to turn right, so it slowed down and waited for vehicles 4 and 5 to leave the conflict zone. Vehicle 3 slowed down due to the deceleration of vehicle 2 to maintain a certain distance. The ego vehicle chose to give way to vehicles 4 and 5, and then drove to the target lane together with vehicle 2 before vehicle 3 reached the conflict zone. It can be seen from the speed curves in Fig. 4(b) that the ego vehicle was in a probing state due to many environmental vehicles in this scenario, and its speed curve presented a trend of repeated acceleration and deceleration. The speeds of vehicles 4 and 5 remained almost unchanged after 3 s. The speed curve of vehicle 2 fluctuated during the right turn. Considering the locations of vehicles 4 and 5 and the right turn trend of vehicle 2, the ego vehicle chose to slow down, give way to vehicles 4 and 5 and pass before vehicle 3 reached the conflict zone.

Scenario 4 There were 5 environmental vehicles. The ego vehicle focused on safety and tended to give way. It can be seen from Fig. 5(a)that when vehicles 1 and 4 accelerated, the ego vehicle first chose to yield. When vehicles 1 and 4 left the conflict zone, vehicle 2 reached the conflict zone, and vehicles 5 and 3 were near the conflict zone. Then the ego vehicle chose to continue to yield and wait for all environmental vehicles to leave the conflict zone before turning left to the target lane. It can be seen from the speed curves in Fig. 5(b) that all five environmental vehicles drove through the intersection at nearly constant speeds, while it can be seen from Fig. 5(a) that the distance between the five vehicles was relatively uniform and small, and consequently the ego vehicle was not able to pass between any two vehicles. The ego vehicle finally adopted a deceleration strategy and accelerated after 12 s. At this time, environmental vehicle 3 had already passed through the conflict zone.

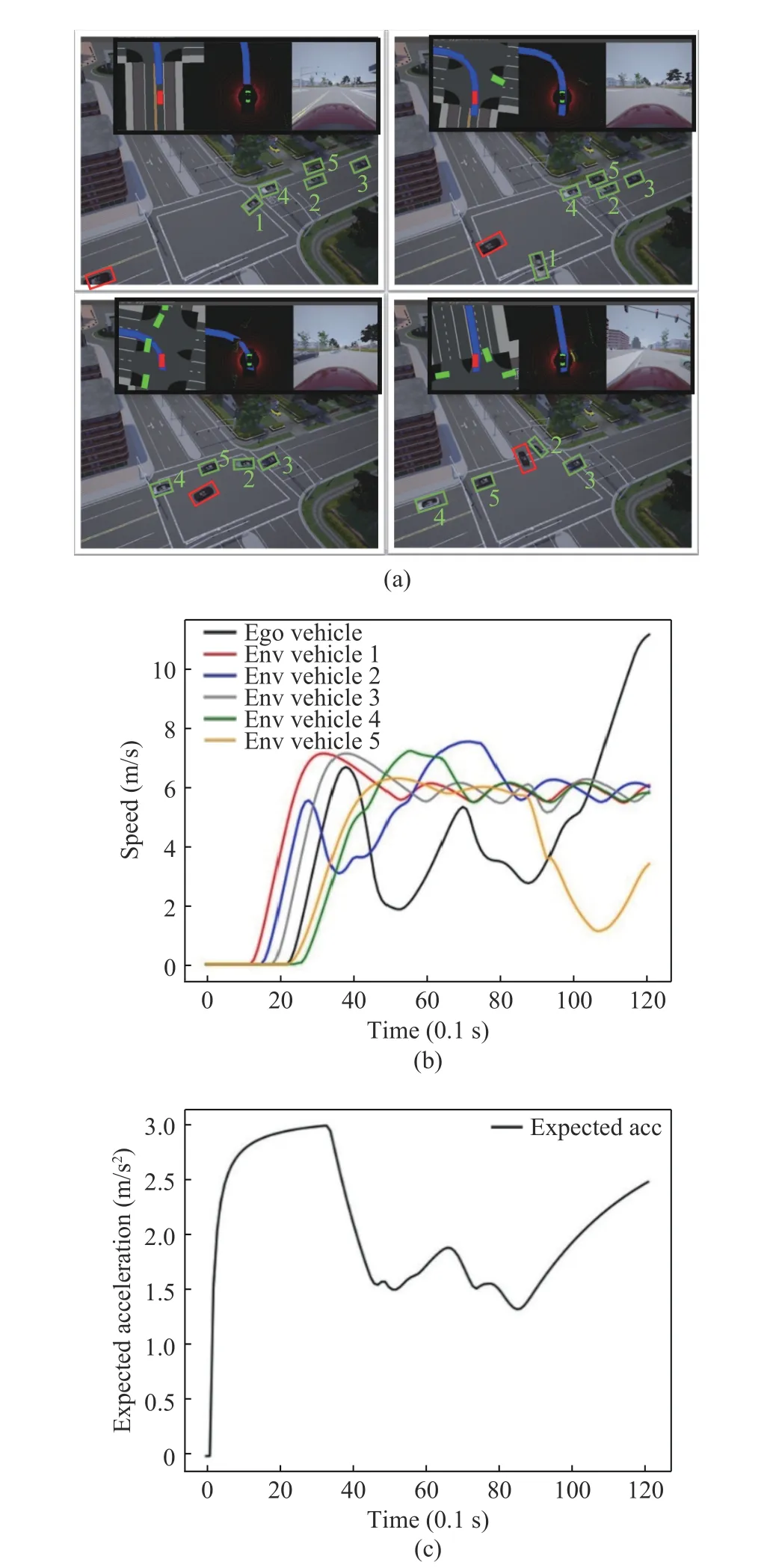
Fig. 4 Scenario 3 test results: (a)Gym-carla scenario 3;(b)speeds of vehicles; (c)longitudinal expected acceleration

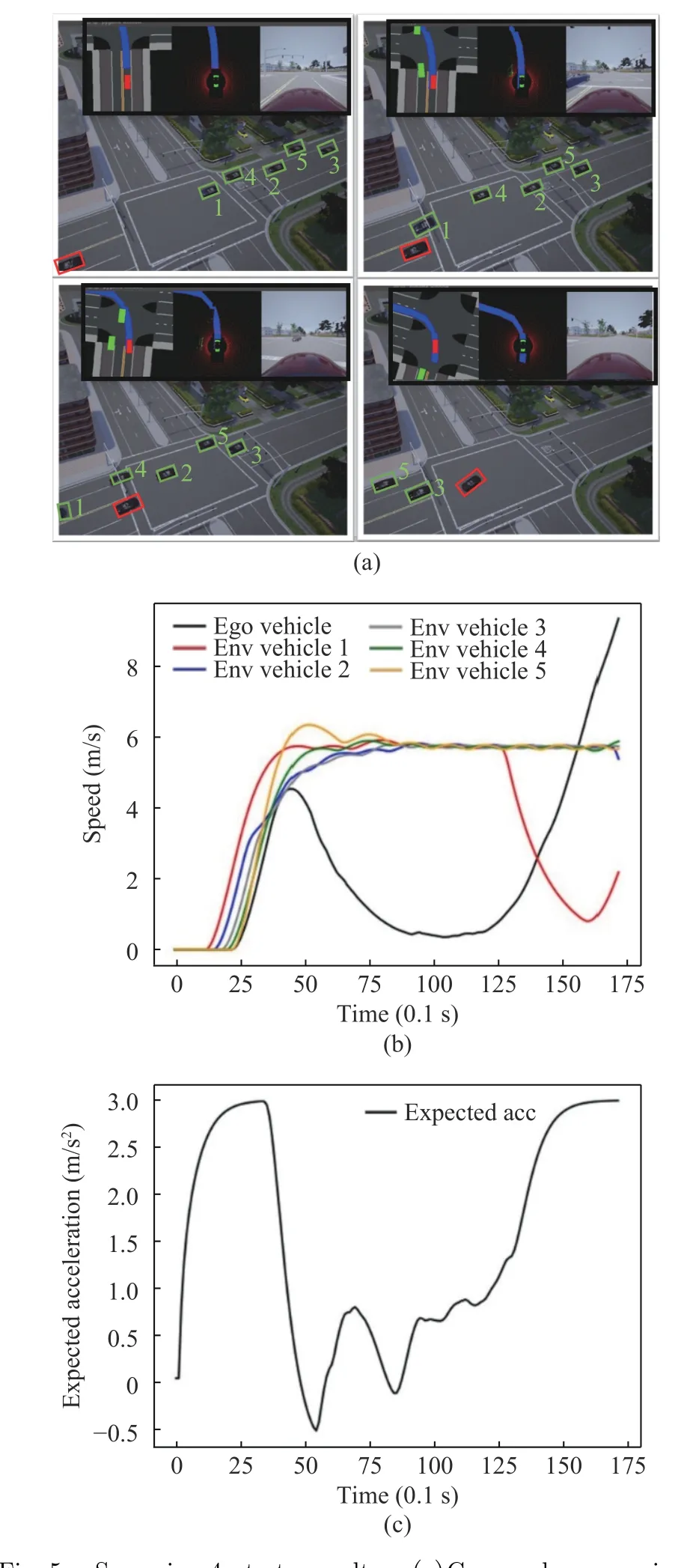
Fig. 5 Scenario 4 test results: (a)Gym-carla scenario 4;(b)speeds of vehicles; (c)longitudinal expected acceleration

From the performances of the ego vehicles in these scenarios, it can be seen that the decisionmaking model of the ego vehicles could already handle random scenarios. It can be concluded that when the decision-making model was trained to convergence, it could meet the requirements of scenario generalization.

4.3 Verification of the T-MAML-DDPG Model

The T-MAML-DDPG model and the T-DDPG model were trained in random and complex intersection scenarios. The number and motion states of environmental vehicles and the initial position of the ego vehicle were randomly set. 1 test was taken after every 20 episodes of training.

It can be seen from Fig. 6 that the two models both converged to certain areas after 80 tests.In the first 20 tests of the T-DDPG model, the episode reward value was around –1 000 or less,and it reached around –500 after 30 tests. The ego vehicle collided when the episode reward value was around –1 000, and the T-DDPG model learned to avoid collision only after 600 episodes of training. The T-MAML-DDPG model had a higher episode reward value in the first few tests,and the episode reward value was about –500 at first, which was equivalent to T-DDPG at the 30th test. Compared with the reward value of TDDPG’s previous tests, T-MAML-DDPG had an improvement of 66.7%, indicating that the policies based on the T-MAML-DDPG model quickly adapted to complex scenarios, met the requirement for safe passage, and had higher passage efficiency as well. From the point of view of convergence speed, the T-DDPG model converged at the 60th test, while the T-MAML-DDPG model tended to converge after 30 tests, giving it a convergence speed about 50% higher than that of TDDPG. It can be seen from Fig. 6 that the convergence areas of the episode reward value of the T-MAML-DDPG and T-DDPG models were very close after the 50th test, indicating that their final performances were close. Nevertheless, the T-MAML-DDPG model was able to quickly adapt to the complex and changeable intersection environment and had higher generalizability.

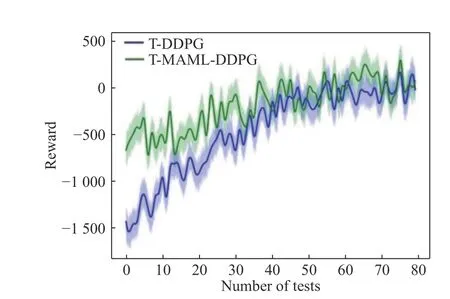
Fig. 6 T-DDPG and T-MAML-DDPG comparison tests

5 Conclusions

The problem is that existing intelligent vehicle behavior decision-making algorithms cannot effectively deal with random states of complex scenarios at urban intersections, leading to poor environmental adaptability. This study developed a training method for the random environments by extending the observation state to a collection of observations for several consecutive frames using a T-DDPG decision algorithm based on a time-series Markov decision process. Experiments showed that compared to the traditional DDPG algorithm, T-DDPG had higher convergence speed and generalizability in complex scenarios.

MAML was incorporated into the T-DDPG algorithm, which improved the training method,and then a decision algorithm (T-MAMLDDPG) based on a secondary gradient was proposed, which enabled intelligent vehicles to adapt to the random states of complex intersection scenarios.

The decision models were verified and compared on the Gym-carla simulation platform.Experiments demonstrated that the T-MAMLDDPG model quickly adapted to complex intersection scenarios. After the same episodes of training, the new model improved adaptability to the environment by 66.7%, and the convergence speed was increased by about 50%.

Future research could be carried out from the following perspectives: in the decision-making process based on a time-series MDP, future studies can look into the optimal number of frames included in the observation state for different scenarios. In addition, the decision models in this paper were only for one single agent. In future research, the decision algorithms can be extended to a multi-agent-oriented strategy,allowing multiple intelligent vehicles to achieve collaborative driving to improve overall traffic efficiency.