Remaining Useful Life Estimation of Lithium-Ion Battery Based on Gaussian Mixture Ensemble Kalman Filter

Ruoxia Li, Siyuan Zhang, Peijun Yang

Abstract: The remaining useful life (RUL) prediction is a crucial indicator for the lithium-ion battery health prognostic. The particle filter (PF), used together with an empirical model, has become one of the most well-accepted techniques for RUL prediction. In this work, a novel filtering algorithm, named the Gaussian mixture model (GMM) - ensemble Kalman filter (EnKF) is proposed.It embeds the Gaussian mixture model in the EnKF framework to cope with the non-Gaussian feature of the system state space, and meanwhile address some of the major shortcomings of the PF.The GMM-EnKF and the PF are both applied on public data sets for RUL prediction and the simulation results show superiority of our proposed approach to the PF.

Keywords: lithium-ion battery; Gaussian mixture model; ensemble Kalman filter (EnKF); remaining useful life (RUL)

1 Introduction

Electric vehicle (EV) industry has witnessed rapid development for the last decade, due to its huge contribution towards reducing carbon emissions and mitigating greenhouse effect. Lithiumion batteries (LIBs) have become the main means of power supply for EVs on account of their high power density, high energy density,and long lifetime [1]. The safety and reliability of EVs relies heavily on close monitoring of the key operating parameters of LIBs such as state of charge (SOC), state of health (SOH) and remaining useful life (RUL).

The definition of RUL is the remaining cycle life before LIBs reach retirement threshold. Usually this threshold is set to be the timing when existing capacity reaches 70%–80% of the nominal capacity. RUL is a strong indicator of the aging degree of LIBs and thus is crucial to the LIBs health diagnosis. Therefore, extensive efforts have been made to explore feasible methods for RUL prediction.

The existing approaches to predict RUL usually fall into two categories, data-driven methods and model-based methods. Data-driven methods usually establish a black-box model between the RUL or its closely correlated parameters such as the LIB capacity and the measurement data such as voltages, current and temperature by using machine learning or statistical approaches [2−4]. These methods circumvent the complexity of modeling the degradation mechanism.However, they depend on massive historical data and the experiment data might possess uncertainty due to various working conditions, which might lead to inaccurate modeling.

The disadvantages of data-driven methods prompt the utilization of a model with explicit mathematical expression in pursuit of RUL prediction. The model-based methods usually fall into two categories, the empirical model based methods and physical model based methods [5].Both methods intend to capture the LIB capacity degradation mechanism by using different modeling approaches. The physical models are constructed based on electrochemical principals,such as the single particle model [6]. The empirical models use mathematical functions to describe the capacity degradation process, such as the polynomial models [7], bi-exponential models, NASA ’s capacity degradation model, etc.Either way, the modeling step is usually followed by a parameter estimation step. Although the physical models tend to yield the most accurate prediction, they often suffer from disadvantages such as high-dimensional, high nonlinearity,etc., which will cause great difficulty in parameter estimation. The empirical model, on the other hand, has much fewer parameters and hence has attracted wide attention.

In recent years, the particle filter(PF) has been extensively used for coefficient estimation for LIB empirical models owing to its well-recognized capability to cope with the non-Gaussian and nonlinear features of systems [8,9]. However,the inherent defects of the PF such as particle degeneracy and robustness problem motivate researchers to develop an improved version of the PF. In light of this idea, Zhang et al. [10] proposed an improved unscented particle filter(UPF) for RUL prediction. They further modified the UPF and used it to estimate the coefficients of the bi-exponential model. The authors demonstrated that the RUL prediction results were superior to both PF and UPF. Ma et al.[11] proposed a Gauss-Hermite particle filter which improved the PF by using the Gauss-Hermite filter to generate the importance probability density function (PDF). Similarly, Duan et al. [12] proposed an extended PF, which uses the extended Kalman filter to generate the sampling function. Qiu et al. [13] included an improved cuckoo search algorithm in the sampling step of prior particles, which helps move the particles closer to maximum likelihood region.

In order to circumvent the tricky issues in the PF, researchers resorted to a novel category of filters, the Gaussian mixture model (GMM)based filters. These filters model the prior, predicted and posterior distributions with the GMM and recursively update the GMM parameters in the Bayesian filtering framework. Several GMM based filtering algorithms have been successfully developed. Chen et al. [14] proposed a mixture Kalman filter and a mixture extended Kalman filter for nonlinear systems. Kotecha et al. [15]proposed a mixture particle filter which used a bank of particle filters to address the non-Gaussian filtering problem. Dovera et al. [16] integrated the GMM into the ensemble Kalman filter framework. This novel filter is derivative free and can provide analytical expression of the posterior distribution.

In this paper, a novel GMM based on ensemble Kalman filter(EnKF), namely the GMMEnKF, is proposed for the RUL prediction. Our proposed filter excels in dealing with the non-Gaussian feature of the states PDF, which is perfect for the highly nonlinear LIB empirical model.Moreover, the ensemble feature of our proposed approach is able to provide full PDF estimation for the RUL instead of a point estimate. We present the application of the proposed estimator to four public datasets from the Prognostics Center of Excellence (PCoE) at NASA Ames Research Center and demonstrate that the GMM-EnKF based prognostic methods are more accurate than the most widely used PF based methods.

2 Ensemble Kalman Filter (EnKF)

The EnKF is first proposed by Evensen et al. [17]to cope with the difficulty of calculating covari-

ance inversion in the Kalman filter for highdimensional systems. It uses an ensemble of particles generated by the Monte Carlo sampling technique to recursively pass on the estimation information. In each iteration, all the statistical information of the posterior PDF, i.e. mean and covariance, is calculated using the particle ensemble. The mathematical details of the EnKF algorithm are presented as follows.

Prediction:

3 Gaussian Mixture Model Based Ensemble Kalman Filter (GMMEnKF)

In this section, a novel GMM-EnKF filtering algorithm is proposed as an extension of the EnKF in the precious section. Similar to the EnKF, the GMM-EnKF also uses a particle ensemble generated from the prior distribution by using the Monte Carlo sampling technique to pass on estimation information. However, in the case of the GMM-EnKF, the prior, predicted and posterior distributions are all modeled as GMM,described as follows

The EM algorithm upgrades maximum likelihood estimation method further for scenarios where there are hidden variables present. In the case of GMM parameter estimation, which Gaussian mode each particle belongs to is the hidden variable. The EM algorithm consists of two steps,an expectation step, namely the E-step, and a maximization step, namely the M-step. In the Estep, the expectation of the log likelihood of the complete data set, namely the Q function, is formulated and in the M-step the Q function is maximized in terms of the unknown parameters.The two steps are performed iteratively until the values of the estimated unknown parameters converge. The mathematical details of the EM algorithm can be found in [19].

4 The Lithium-Ion Battery RUL Prediction

4.1 The Capacity Degradation Model for the Lithium-Ion Battery

In this work, we use the bi-exponential model to mimic the battery degradation trend. The mathematical function model is described as follows.

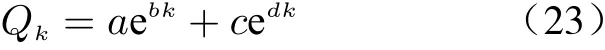
Here,Qkis the capacity of the battery,a,b,c,dare the coefficients to be estimated,kis the number of the charging-discharging cycle.

4.2 The RUL Prediction Based on the GMMEnKF

The GMM-EnKF algorithm proposed in section 3 is used for estimating the coefficients of the biexponential model. The state transition model and the measurement model are constructed as follows

The capacity measurements are obtained from the experiment data of #5, #6, #7 and#18 batteries provided by the NASA Ames Prognostics Center of Excellence [20]. The chargingdischarging experiments of the four batteries are repetitively conducted in three sets of working conditions under room temperature.

In the following sections, all simulation results presented use the same number of particles, which is 200, and the same number of Gaussian modes, which is 2. We compare the GMMEnKF estimation results with the most widely used PF in existing work and show the superiority of our proposed method.

4.3 Simulation Results Using the GMM-EnKF and PF

In this section, the GMM-EnKF and PF are used to estimate the parameters,ak, bk, ck, dk, respectively based on the test data of the #5, #6, #7 and #18 batteries. Because of its Monte Carlo sampling based feature, the PF is now the most widely used method for RUL distribution estimation, and hence is used for comparison. As the#7 and #18 batteries do not have data below the failure threshold, only the capacity prediction is conducted for them. The rest two batteries are used for the RUL prediction. Both GMMEnKF and PF use the same initial values ofak, bk, ck, dk, which are obtained by fitting the degradation curve using the curve fitting toolbox of the MATLAB. The parameter initial values of the four batteries are listed in Tab. 1. Both filters use the same number of particles, which is 200.

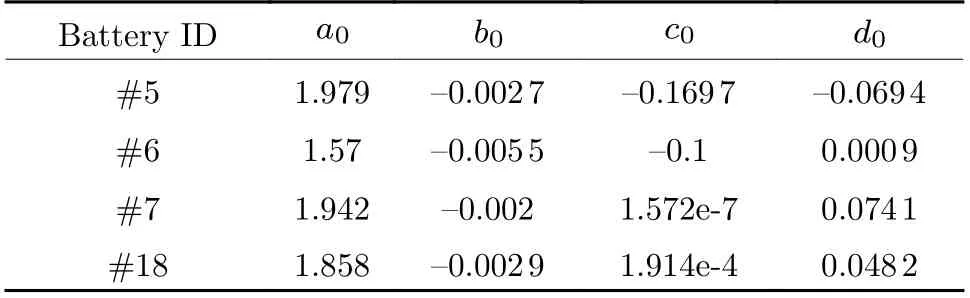
Tab. 1 The initial values of the parameters for filtering

Fig. 1 shows the comparison of prediction results using the GMM-EnKF and PF. The values ofak, bk, ck, dkused for RUL prediction are all selected to be the estimates obtained at the 80th cycle, which are shown in Tab. 2. Both filtering methods are able to capture the degradation trend, with the GMM-EnKF fitting better.

Fig. 1 Comparison of the prediction results using the GMMEnKF and the PF: (a) battery #5; (b) battery #6; (c)battery #7; (d) battery #18

The root mean square errors (RMSE) of prediction results using two filters are listed in Tab. 3. As is shown in Tab. 3, the GMM-EnKF outperforms the PF for all batteries, which demonstrates the effectiveness of our proposed approach.

Tab. 2 The posterior parameters used for capacity prediction for four batteries

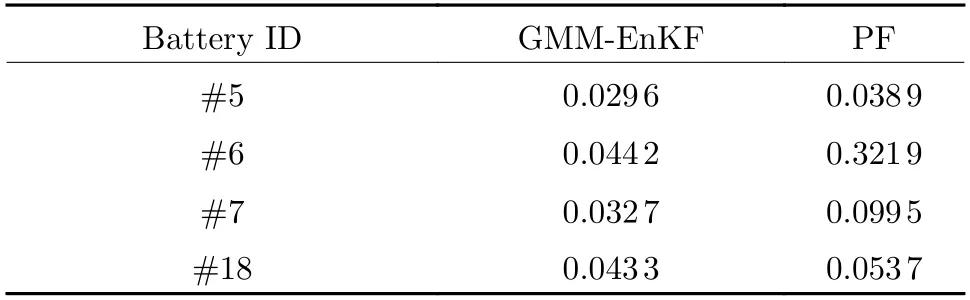
Tab. 3 The prediction RMSE of the two filtering methods

The RUL can be further predicted based on the capacity estimate. It can be determined by comparing the estimated capacity of all cycles with the failure threshold value, which is 1.299 5 for #5 battery and 1.424 7 for #6 battery,respectively. The true RUL values and the estimated RUL values are listed in Tab. 4. The relative prediction error (RPE) is also provided in Tab. 4. The RUL estimation results also demonstrate significant superiority of our proposed method to the PF. The RPE is defined as follows

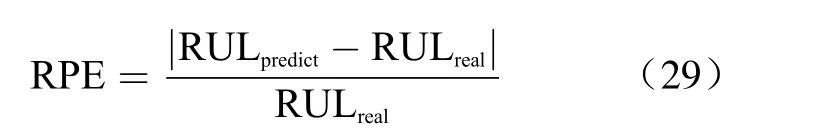
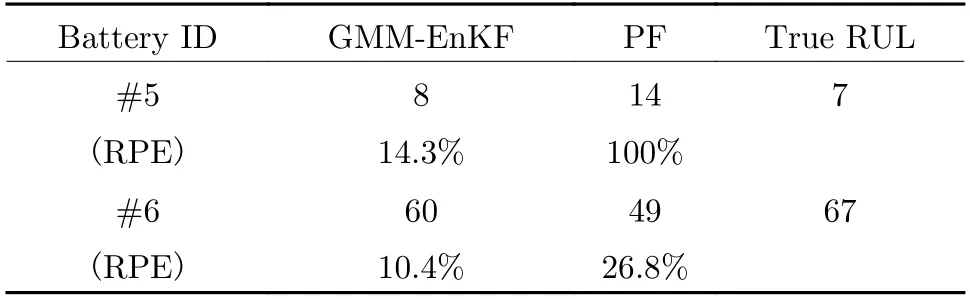
Tab. 4 The true RUL and the estimated RUL of #5 and #6 batteries using the GMM-EnKF and the PF

After obtaining the point estimate of the RUL, we can go further to obtain the estimated distribution of the RUL. Fig. 2 shows the estimated RUL distributions of #5 battery using the GMM-EnKF and the PF.

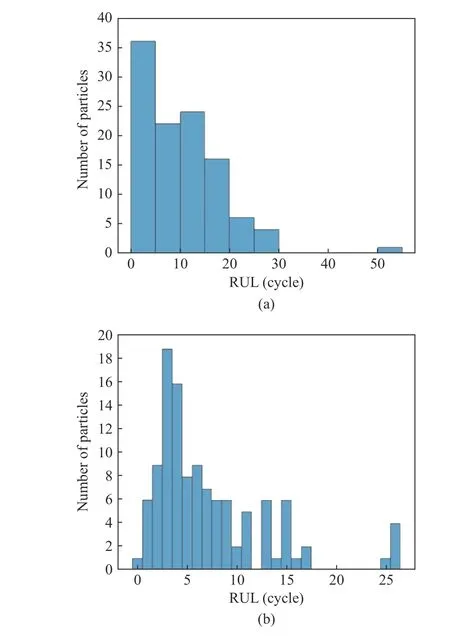
Fig. 2 The estimated RUL distributions of the #5 battery using the GMM-EnKF and PF: (a) #5 battery RUL distribution using the GMM-EnKF; (b) #5 battery RUL distribution using the PF

Fig. 3 shows the estimated RUL distributions of #6 battery using the GMM-EnKF and the PF. Although the two approaches can both obtain the posterior distributions of RUL, the GMM-EnKF method clearly renders more effective particles which are located closer to the true value. That is the main reason why the GMMEnKF is able to yield better estimate.

The superiority of the GMM-EnKF to the PF in capacity estimation and RUL prediction comes from two aspects:

1) The GMM-EnKF does not have to deal with particle degeneracy problem, which is, however, a major concern in the PF, especially when the initial particles are not chosen properly. The GMM-EnKF is free from this issue because of its Kalman gain based update mechanism.

Fig. 3 The estimated RUL distributions of the #6 battery using the GMM-EnKF and the PF: (a) #6 battery RUL distribution using the GMM-EnKF; (b) #6 battery RUL distribution using the PF

2) The GMM-EnKF is less sensitive to the uncertainty caused by the poor prior information.Although in this work a fitting step using the MATLAB toolbox is performed beforehand to contain the uncertainty, the performance of the PF can still be influenced by fine-tuning of the initial values. The GMM-EnKF, on the other hand, can perform well even when the initial values are poor.

In summery, these two advantages enable the GMM-EnKF to provide more accurate estimate of the capacity, leading to more accurate RUL prediction.

5 Conclusion

In this work, a novel filtering algorithm, the GMM-EnKF, is proposed to perform the RUL prediction. This filter extends the standard EnKF to the scenario where the state space can not be described as a Gaussian distribution due to high linearity, non-Gaussian noises, etc. As the battery empirical model usually presents high nonlinearity, our proposed method is a suited tool for RUL prediction. It can be deemed as an excellent replacement of the widely used PF. The performance of the proposed filtering approach is demonstrated based on the capacity test data from NASA Ames Research Center. The capacity estimation RMSE and RUL prediction error are compared with the PF under the same simulation conditions. The simulation results show an evident advantage of the proposed approach over the PF.