A Causal Fusion Inference Method for Industrial Alarm Root Cause Analysis Based on Process Topology and Alarm Event Data

Pan Zhang, Wenkai Hu, Xiangxiang Zhang, Jianqi An

Abstract: Modern industrial systems are usually in large scale, consisting of massive components and variables that form a complex system topology. Owing to the interconnections among devices, a fault may occur and propagate to exert widespread influences and lead to a variety of alarms.Obtaining the root causes of alarms is beneficial to the decision supports in making corrective alarm responses. Existing data-driven methods for alarm root cause analysis detect causal relations among alarms mainly based on historical alarm event data. To improve the accuracy, this paper proposes a causal fusion inference method for industrial alarm root cause analysis based on process topology and alarm events. A Granger causality inference method considering process topology is exploited to find out the causal relations among alarms. The topological nodes are used as the inputs of the model, and the alarm causal adjacency matrix between alarm variables is obtained by calculating the likelihood of the topological Hawkes process. The root cause is then obtained from the directed acyclic graph (DAG) among alarm variables. The effectiveness of the proposed method is verified by simulations based on both a numerical example and the Tennessee Eastman process (TEP)model.

Keywords: roots cause analysis; causality inference; process topology; alarm events

1 Introduction

Modern industrial systems are usually in large scale, consisting of massive components and variables that form a complex system topology.Owing to the interconnections among devices, a fault may occur and propagate to exert widespread influences and lead to a variety of alarms.Obtaining the root causes of alarms is beneficial to the decision supports in making corrective alarm responses. Especially, as the industrial facilities become larger and the number of alarms is increasing, accurately detecting the root causes for alarms spreading in different units or processes is a rather complex task [1]. Many well formulated data-driven methods for alarm root cause analysis fall into correlation and causality analysis.

Alarm correlation analysis detects correlations between two or among more alarm variables. Different correlation measurements were defined for alarms, such as the Jaccard coefficient [2], Sorgenfrei coefficient [3], Pearson's correlation coefficient [4], and Dice coefficient [5].The random delays among the occurrences of alarms usually lead to errors in the calculation of correlation degrees [6]. To cope with this issue,an evaluation method based on kernel density was proposed to reduce the impact of non-fixed delay [6, 7]. Further, in view of the high computational complexity in the detection of correlated alarms, an association analysis method based on block matching similarity was proposed [8]. However, alarm correlation analysis only considers the similarity while ignoring the directionality,and thus it is difficult to find the propagation of abnormalities.

By contrast, causal inference can discover causal relations and is more suitable for alarm root cause analysis. Prevalent causality analysis methods include Granger causality analysis,transfer entropy (TE), and Bayesian network.Granger causality analysis is capable of detecting causal relations for linear processes. Many improved Granger causality analysis methods have been proposed and applied to industrial fields [9, 10]. In addition, TE and Bayesian network have also been commonly used in root cause analysis. Many variants of TE have been proposed, such as the symbolic TE [11], information granulation based TE [12], and modified TE for non-fixed delays [13]. Bayesian network-based methods, such as dynamic Bayesian network [14],Naive Bayesian classifier [15], and Bayesian belief network [16], were developed to find alarm root causes by learning conditional probabilities and constructing directed acyclic graph (DAG).

In a complex industrial facility, devices are physically connected to form a process topology,and abnormalities may propagate easily through such a complex network to trigger a variety of alarms. Existing data-driven methods for alarm root cause analysis detect causal relations among alarms mainly based on historical alarm events.The process topology on the causal relations among alarm variables is rarely considered. To improve the accuracy, this paper proposes a causal fusion inference method for industrial alarm root cause analysis based on process topology and alarm event data. A Granger causality inference method considering process topology is exploited to find out the causal relations among alarms. The process topology is used as the input of the model, and the alarm causal adjacency matrix among alarm variables is obtained by calculating the likelihood of the topological Hawkes process. The root cause is then obtained from the DAG among alarm variables. The effectiveness of the proposed method is verified by simulations based on both a numerical example and the Tennessee Eastman process (TEP) model.

Section 2 mainly describes the problem and research motivation. Section 3 presents the proposed method for alarm root cause analysis. Section 4 verifies the effectiveness of the proposed method by simulations, followed by a summary in Section 5.

2 Motivation

Connectivity shows a physical or information linkage among process devices [17]. As process connection becomes complicated in complex industrial systems, when an abnormality occurs, a series of alarms may happen and easily spread through the complex process topology, making it difficult for the operator to find the alarm root causes. Existing data-driven methods for alarm root cause analysis detect causal relations between alarms mainly based on historical alarm event data. The process topology on the causal relations between alarm variables is rarely considered. Therefore, when a fault in a complex industrial process causes chain effects and leads to alarm floods, an effective causal inference method is needed to quickly and accurately find alarm root causes, which can help operators to detect faults and fix them in time.

This paper proposes a causal fusion inference method for industrial alarm root cause analysis based on process topology and alarm event data. The framework of the proposed method to detect causal relations among alarms is shown in Fig. 1. The piping and instrumentation diagram(P&ID)/process flow diagram (PFD) is converted to a process topological adjacency matrix.Alarm events are obtained and chattering alarms are reduced. The process topological adjacency matrix is combined with the alarm events through the alarm causality fusion inference, and the alarm causal graph is obtained.

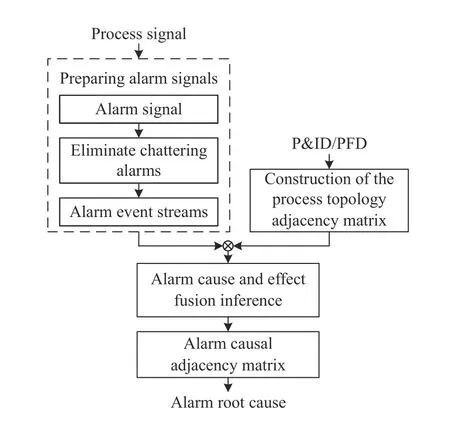
Fig. 1 Framework of the method to detect causal relations between alarms

3 The Proposed Method

This section proposes a causality inference method based on the process topology and alarm event data, including construction of the process topological adjacency matrix, preparing alarm signals, and alarm causality fusion inference.

3.1 Construction of the Process Topological Adjacency Matrix

The main resources for establishing process topology are process flow diagrams (PFDs) and piping and instrumentation diagrams (P&IDs); thus they should be converted into standard formats,such as adjacency matrix digraphs, and semantic web models, which are easily accessible and computer-friendly [17].

Some common approaches have been proposed to capture topology from process knowledge, such as the signed directed graph (SDG)model building, rule-based modeling, and extracting process topology from Web language. Details of these approaches can be referred to reference [17].

Fig. 2 presents an example of a complex process topology. The topology is presented as an undirected graph, where devices are equivalent to nodes in the network. TheGUrepresents process topology, whereU={u1,u2,··· ,ui,···}indicates unit (or plant area) set,uiis thei- th unit,EUis the undirected edge set. Here,GU=(U,EU) is represented by the process topological adjacency matrixB, i.e.,

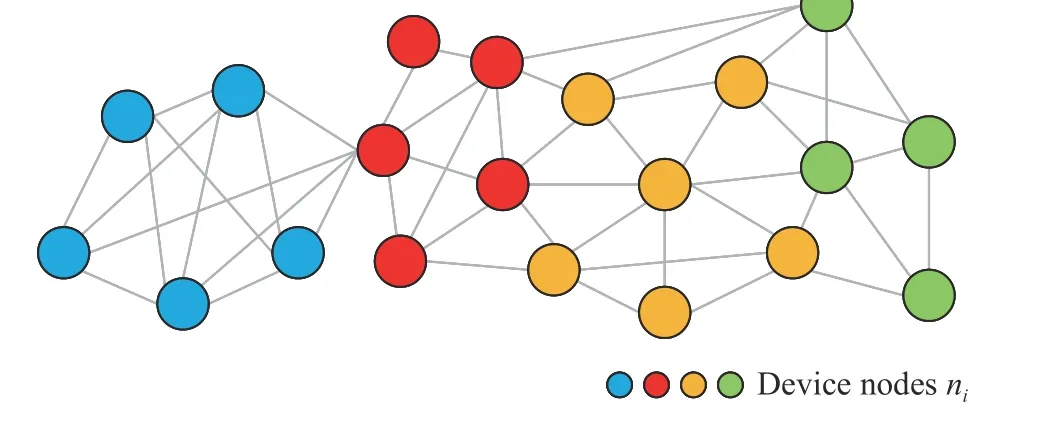
Fig. 2 An example of a complex process topology

whereBij=1 represents that thei- th rowuiconnects with thej-th columnuj. The matrixBis symmetric, i.e.,Bij=Bji.

In a real industrial system, there are usually quite a few units corresponding to different processes, and each unit is composed of many devices. Given two unitsui,uj, if an alarm eventvhmeets condition (vh ∈Vi)∪(vh ∈Vj), then there is an edge connecting unituianduj(h,i,j ∈N*), i.e.,Bij=1, whereViandVjdenote the sets of alarms in unituianduj, respectively.TheV～=[V1,V2,··· ,Vi,···] is the sequence of the sets of alarm in the set of unitU, whereVidenotes the sets of alarms in unitui. According to P&ID and PFD, a complex industrial system is divided into multiple unitsui,(i=1,2,...), and the unit setUis obtained. The alarm variablesvh,(h=1,2,···)flowing into and out of the unitujare added to the set of alarmvj, and the sequenceV～is obtained.

3.2 Preparing Alarm Signals

The alarm signal is usually in two typical forms [6] : 1) the alarm signal that takes the value of 1 only at the occurrences time instant; 2) the alarm signal that takes the value of 1 over the alarming time duration. Alarm information is commonly historized in the form of alarm event streams [18] in an industrial alarm system. An alarm event stream captures the alarm transient events. Formally, an alarm is generally generated based on the associated process signal, and can be obtained by setting the high or low limit, i.e.,

As a result, chattering alarms can be effectively reduced by delay timers.

3.3 Alarm Causality Fusion Inference

Causality among process variables can be found through process data as well as process knowledge; thus a directed acyclic graph (DAG)is used to describe the causal relations between

Fig. 3 An example of a DAG representing alarm causal relations

4 Case Studies

In this section, a numerical example and the benchmark Tennessee Eastman process (TEP)model are used to verify the effectiveness and feasibility of the proposed method in industrial alarm root cause analysis.

4.1 Case 1: Numerical Case Study

The numerical example firstly constructs three device nodesn0,n1, andn2, and then connectsn0ton1,n1andn2to construct the node topology.Three alarm signalsx,y, andzare produced based on a multivariate Hawkes process [24], and the causal relations are shown in Fig. 4, where the three signals are placed in three nodes.

Fig. 4 Causal relations among alarms in different device nodes in the numerical example

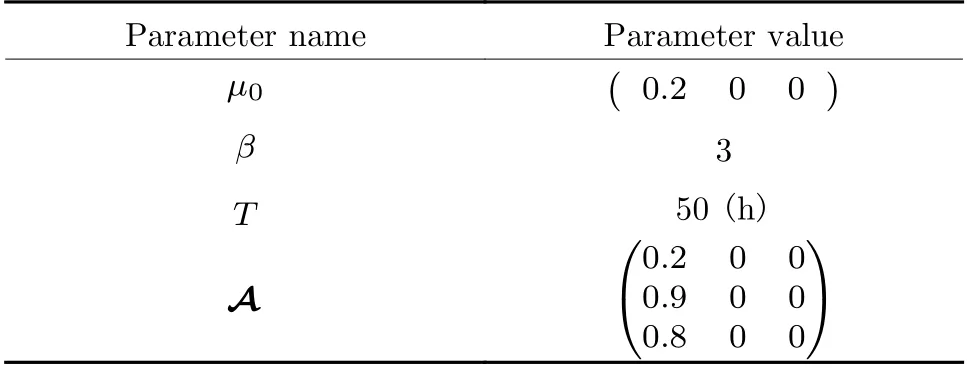
Tab. 1 Model parameters

The nodesn0,n1, andn2formGUand alarm eventsx,y, andzformGV. Eventually, the simulation dataset is formed. The process topological adjacency matrixBis

Fig. 5 The alarm signals x, y, and z in nodes 0, 1, and 2: (a)node 0, alarm z; (b) node 1, alarm x; (c) node 2, alarm y

4.2 Case 2: TE Process

TE process model is a realistic simulation program of a chemical plant that is widely accepted as a benchmark for control and monitoring studies [25]. The process flow diagram of TE process is shown in Fig. 6. There are 52 variables, including 41 detection variables and 11 operational variables. The variable description in Fig. 6 is explained in detail in [25]. The model is mainly constructed by five units, i.e. reactor(u1), condenser(u2) , compressor(u3) , separator(u4), and stripper(u5), which are interconnected, and their relations are shown in Tab. 2, forming the process topology.

Fig. 6 Process flow diagram of the TE process [25]

Tab. 2 Division of 5 units

The exploited TE Process model contains 22 faults. Fault 1(namely, the step in component A/C feed ratio, B composition constant) was used, and 22 variables from 5 units in Tab. 3 were selected in the case study. The process variables and configured alarm limits are listed in Tab. 3.

Six thousand samples of 22 variables are collected from the simulation platform. The data normalized to [-1,1] are shown in Fig. 7. The normalized signals from sample 1 000 to 2000 are ploted together with denoised signals and alarm limits. The process signals of variablesF2,F3,F19,andC20show non-significant variations in the presence of fault 1. Thus, they are not included in this case study.

According to Fig. 9, the DAG of 18 variables in the presence of fault 1 is drawn in Fig. 10,from which it can be clearly found that there are four root cause variables. Fault 1 only changes the A/C feed ratio, and the total A/B/C flow rate rarely changes. According to Fig. 6, it canbe analyzed that when fault 1 occurs, variables such asF5andF10that monitor flow changes will not be the first to generate an alarm. The A/C feed will enter the Stripper first and finally the Reactor, whereT18monitors the Stripper temperature andT9monitors the Reactor temperature,as well asT18alarms beforeT9. Through analysis,T18is the major root cause variable. Theoretically, when fault 1 occurs,T18in Stripper is affected firstly, and then a chain reaction of variables propagates through the device network.According to the results, the proposed method is

demonstrated to be effective.

Tab. 3 Alarm high/low limits and on-delay timer thresholdτvh

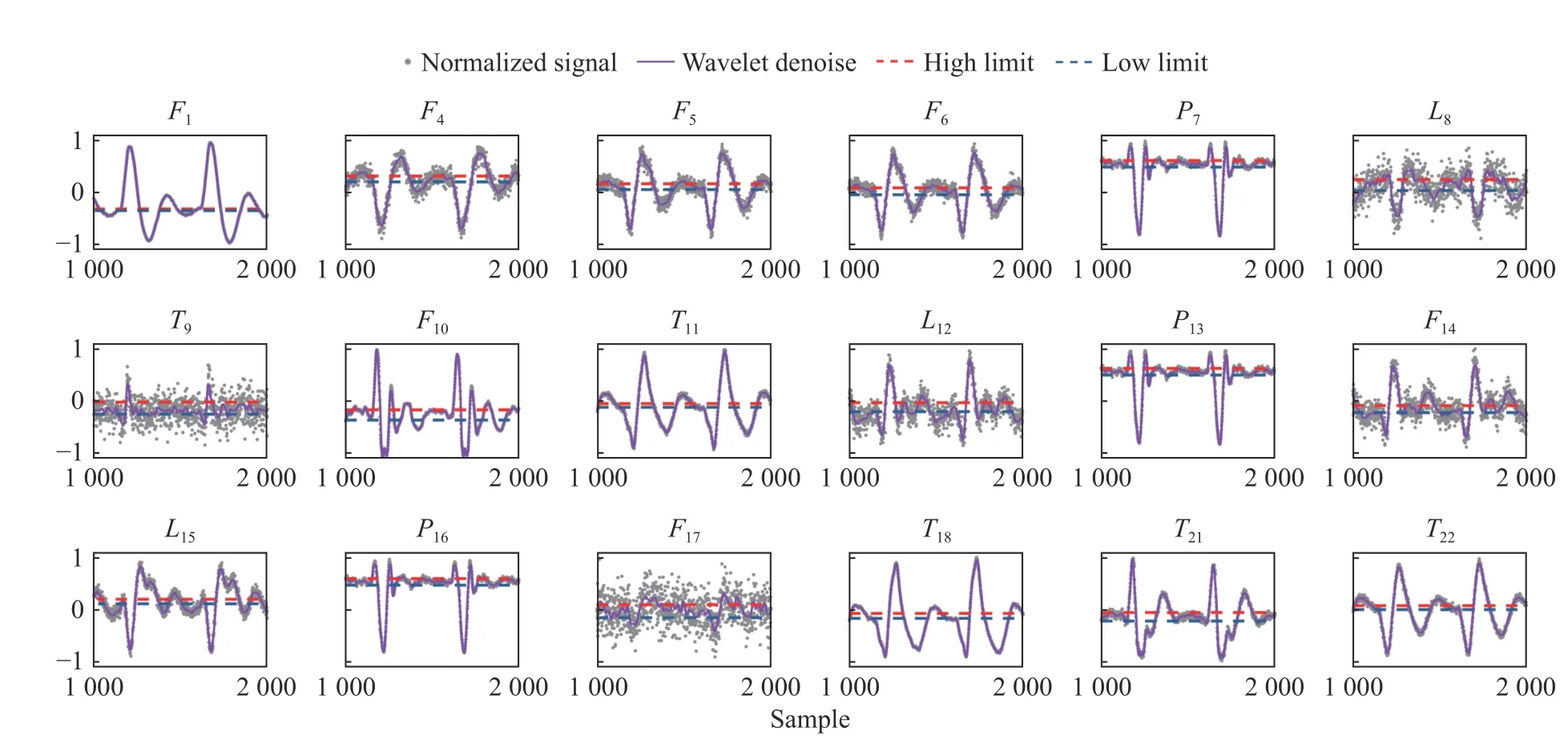
Fig. 7 TEP signals for 18 variables

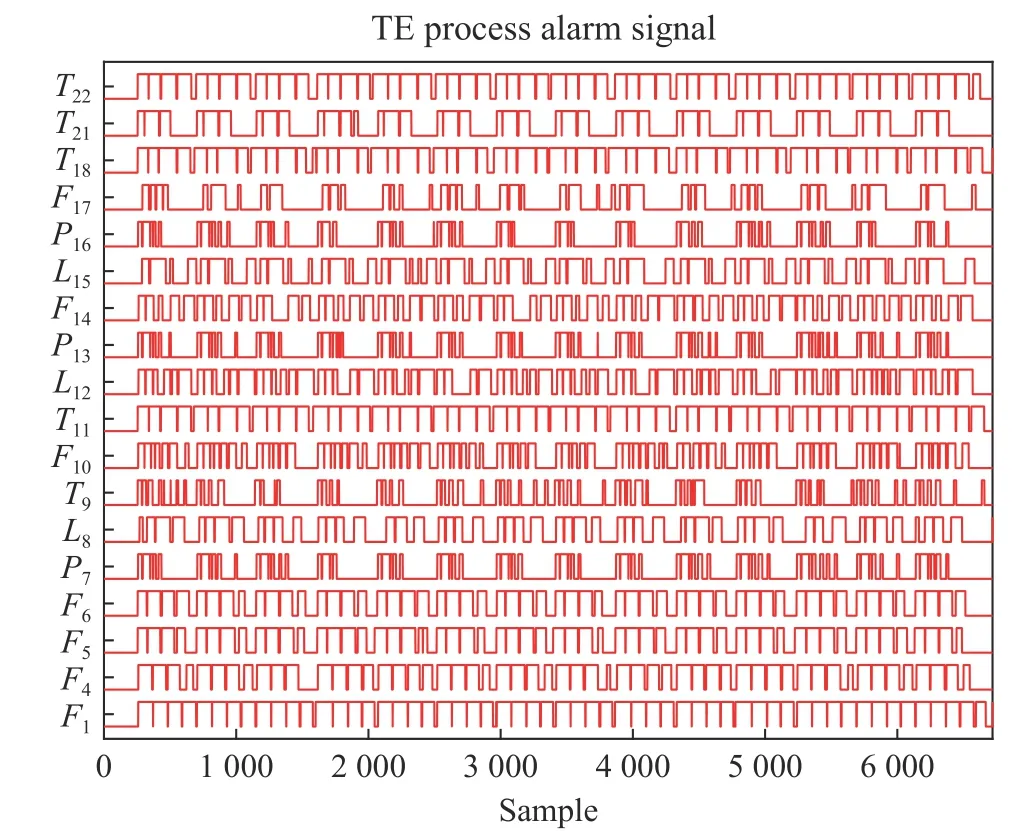
Fig. 8 Alarm signals for 18 variables

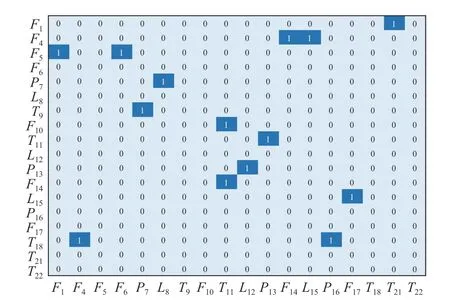
Fig. 9 Causality diagram for 18 variables

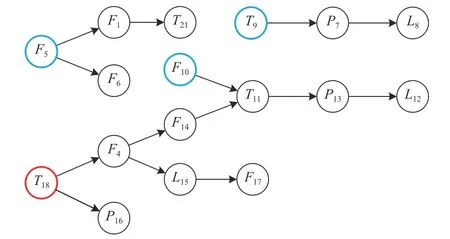
Fig. 10 DAG of 18 variables in fault 1

5 Conclusion

In this paper, a causal fusion inference method for industrial alarm root cause analysis is proposed based on process topology and alarm events. The P&ID/PFD is converted to a process topological adjacency matrix. Alarm events are obtained and chattering alarms are reduced.The process topological adjacency matrix is combined with the alarm events through the alarm causality fusion inference, and the alarm causal graph is obtained. Two case studies are given to illustrate the effectiveness of the proposed methods. The root cause alarm variables are obtained through the root cause analysis of the directed acyclic graph.