An Improved Repetitive Control Strategy for LCL Grid-Connected Inverter

Ning He, Chenlu Song, Feng Gao, Cheng Qian

Abstract: This paper proposes a cascade repetitive control strategy based on odd internal mode,and combines it with proportional-integral (PI) control to establish a compound repetitive control system for improving the quality of grid connected current of LCL grid connected inverter. More specifically, the proposed method could effectively improve the control effect of grid-connected current of LCL inverter, restrain current harmonics and reduce the distortion rate of grid-connected current. Simulation experiment is conducted to verify the proposed repetitive control strategy, and the verification results show that, compared with traditional PI control, the proposed improved compound repetitive control strategy has a higher response speed, and the steady-state and dynamic performance have also been significantly improved.

Keywords: grid-connected; inverter LCL filter; harmonic suppression; repetitive control

1 Introduction

With the continuous growth of energy demand and the concern of environmental problems in various countries, the renewable energy plays an important role in the future energy development.Distributed generation is of great significance for energy emission reduction and sustainable development with the advantages of using various renewable energy sources, and the wind power and photovoltaic power represented distributed power generation system needs to be connected with the grid via grid-connected inverters to realize the transmission. Grid-connected inverter, an important power electronic equipment in distributed power generation system, has always been a hot spot in the research field [1].

As one of the core components of distributed generation system, grid-connected inverter directly determines the quality of grid-connected current. The harmonic components and scarce sine degree in the grid-connected current will bring trouble to the grid, and further cause harm to the power system and affect the effective utilization rate of power supply. Grid-connected current control technology directly determines the quality of grid-connected waveform. Therefore, many researchers have focused on the research on current control method [2−4].

Firstly, different output filters will lead to different selection of control methods from the view of the filter structure topologically, and the commonly used grid-connected inverters mainly includes L type and LCL type [5−7], in which the structure of L-type grid-connected inverter is simple and the control method is mature. However, in order to obtain sufficiently large attenuation amplitude at switching frequency, the filter inductance is very large, which makes the system bulky and costly, in addition, LCL grid-connected inverter has the characteristics of fast attenuation in high frequency band, and can reduce switching frequency harmonics with small hardware volume [8].

In order to reduce the harmonic component of grid-connected current, researches on its control technology have been conducted extensively.Therefore, a number of control techniques are applied to control the grid-connected current of grid-connected inverters, such as proportionalintegral-differential control [9], fuzzy control [10],hysteresis current control [11], proportional-integral control [12], model predictive control [13−15],deadbeat control [16], proportional resonance control [17], repetitive control [18−19], etc.

The repetitive control has high steady-state accuracy and good interference suppression ability, which has obvious suppression effect on the periodic disturbance caused by the nonlinear load of the inverter, and can realize the tracking of the periodic signal without static error. Some scholars have adopted a scheme combining proportional-integral (PI) with repetitive control[20−21], i.e., the double closed-loop control strategy of PI control and repetitive control was adopted to improve the dynamic performance of the system. The results showed that the stability and anti-interference performance of the system were improved. Literature [22] introduced repetitive control into the adaptive control algorithm,which improved the control effect and stability of the system. However, this method was too complicated and the control link was difficult to realize. Literature [23] has achieved the suppression of 6K+1 harmonic, but the phase-locked loop was needed to carry out coordinate transformation of the system, resulting in low tolerance to noise.

Based on the problems considered above,this paper proposes a cascade repetitive control strategy based on odd internal mode, and combines it with PI control to establish a compound repetitive control system for improving the quality of grid-connected current of LCL grid-connected inverter. The proposed method could effectively improve the control effect of grid-connected current of LCL grid-connected inverter,restrains current harmonics and reduces the distortion rate of grid-connected current. Comparison with the existing method has also been conducted to verify the effectiveness and superiority of the proposed strategy. It is worth noting that the novelty of this paper is incorporating the odd internal model and cascaded structure into the standard repetitive controller. Note that since the utilized odd internal model and cascaded structure could accelerate the dynamic response of the system and shorten the delay time when the outer loop of the repetitive controller starts to correct the tracking error, the proposed improved repetitive controller could effectively improve the tracking speed and robustness of the considered system while reduces the steady-state error.

2 Mathematical Model of LCL Grid-Connected Inverter

The main circuit topology of three-phase gridconnected inverter is shown in Fig. 1. In Fig. 1,VT1-VT6 represent the six IGBT switch tubes of the three-phase inverter bridge.Vdcis the input voltage at the DC side,Cdcis the absorption capacitance of the DC bus,Lfa,LfbandLfcare the filter inductors at the inverter side,Lga,LgbandLgcare the filter inductors at the grid side, andCfa,CfbandCfcare the filter capacitors. RL represents the internal resistance of filter inductorLf,Rgrepresents the internal resistance of filter inductor.Lg,Lf,Cf,Lgconstitute a third-order LCL filter.

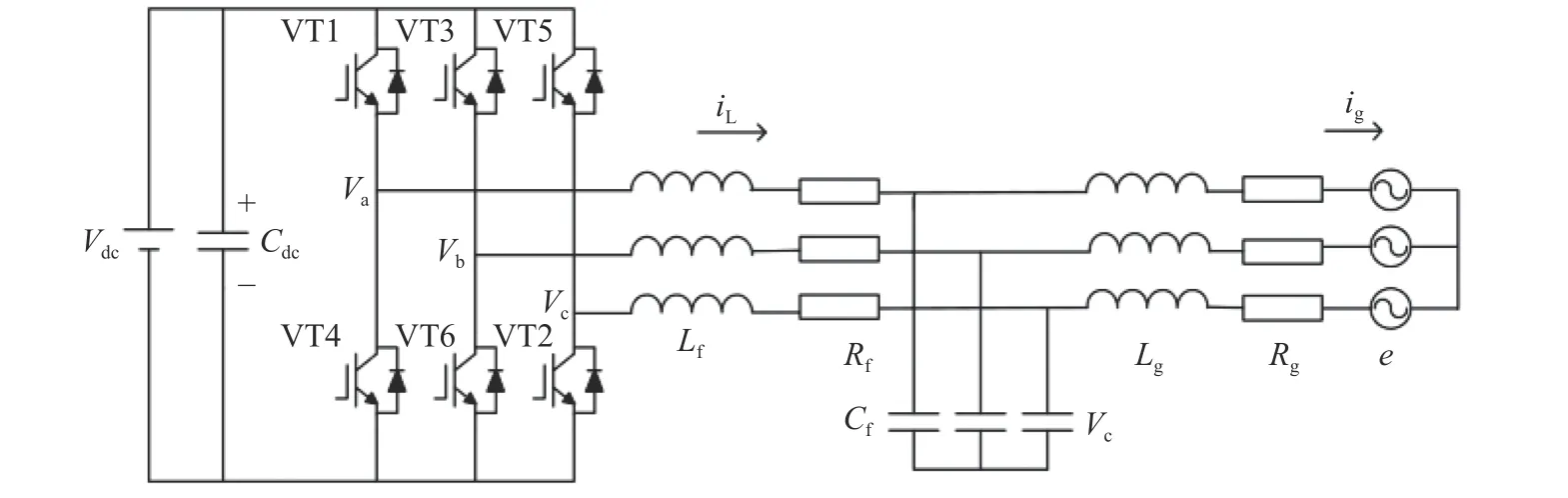
Fig. 1 Main circuit topology of three-phase LCL grid-connected inverter

The current vector control is used to decouple the active and reactive current, usually in the synchronous rotation of thed-qcoordinate system, to convert the control quantity into a direct current. Assuming that three-phase power grid voltage is stable and symmetrical, selecting inverter side current, grid current and voltage as state quantities, the state equation of grid-connected inverter system in three-phase static coordinate system can be obtained as

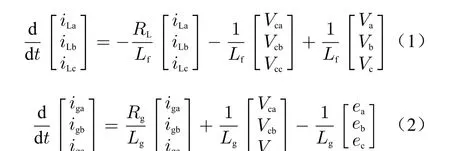
Va,Vb, andVcrepresent the output voltage of the inverter side,Vca,Vcb, andVccrepresent the voltage on the filter capacitor of the three-phase AC side, andea,eb, andecrepresent the voltage of the three-phase power grid.

Mathematical model of grid-connected inverter in three-phase static coordinate system can be converted into that of rotating coordinate system through Clark transform and Park transform, shown as

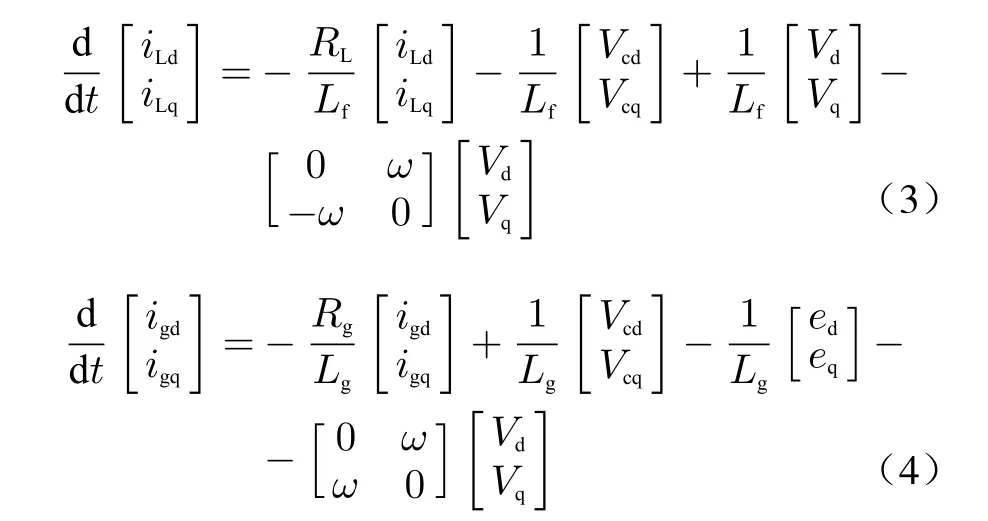
According to the mathematical model of the inverter, after the elimination of coupling phaseiLdandiLqby LCL filter [24], the transfer function of the three-phase grid-connected inverter system from the output voltageVto the gridconnected currentigin the synchronous rotating coordinate system could be obtained as

3 Repetitive Control Strategy for LCL Grid-Connected Inverters

3.1 Traditional Repetitive Control Strategy

Repetitive control is a control method based on internal model principle, which means that the model of external input signal is added to the closed-loop system for self-regulation. In the application of repetitive control, the discrete form of its internal model is shown in Fig. 2.

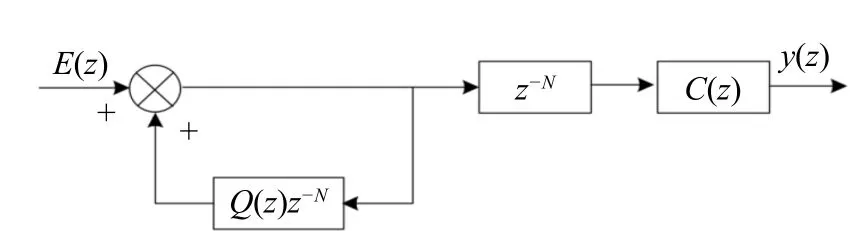
Fig. 2 Traditional repetitive control structure

The transfer function of traditional repetitive control is

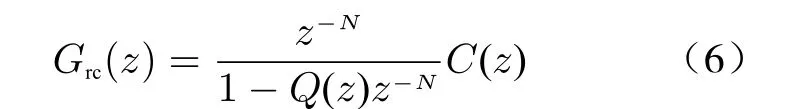
whereNrepresents the sampling times of the system in a complete cycle,Q(z) is low pass filter,andC(z) is the compensator designed for the control object, including gainkrof the compensator, phase lead compensatorzMfor compensating system phase lag and filterS(z). Detailed parameter design forC(z) will be carried out later.

3.2 Improved Repetitive Control Strategy

In power system, it is mainly to control odd harmonics. In order to effectively reduce odd harmonics, an improved repetitive control internal model is proposed, which only selects 1/2 of the sampling times of a period. It can accelerate the dynamic performance of the system and shorten the delay time by half. Fig. 3 shows the improved repetitive control structure.

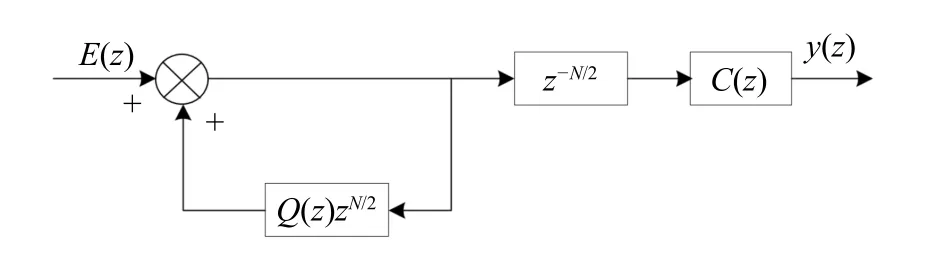
Fig. 3 Improved repetitive control structure

Normally, PI controller is employed in LCL grid-connected inverter to suppress voltage harmonics in power grid. Note that the reason of choosing PI control rather than PID control is that given the considered system, PI control may be enough to achieve the objective of improving the response speed [25], and the addition of a differentiation loop may possibly lead to high frequency oscillation, which could cause the instability of the system and increase the complexity of parameter tuning. Although the response speed of PI control is fast, the steady-state accuracy is not high, and the waveform distortion is large. The repetitive control has good steadystate performance and the output waveform THD is very low. However, due to its characteristic of periodic delay, its dynamic characteristics are relatively poor, and the response speed cannot meet the requirements. Therefore, given the above analysis, it is desired to combine the PI control and repetitive control to construct an improved repetitive control, in which the PI regulator is used to improve the dynamic performance of the system and reduce the oscillation and overshoot when the system is disturbed, and the repetitive control is adopted to reduce the distortion caused by periodic disturbance and reducing the THD of the system.

According to the different positions of the repetitive control, the parallel structure or plugin structure is generally adopted. Here, the cascaded compound repetitive controller is introduced, and the output of the repetitive controller is used as the reference value of the instantaneous value control, and the instantaneous value controller generates the control signal. The control system block diagram of LCL grid-connected inverter is shown in Fig. 4.

In Fig. 4,d(z) is the periodic disturbance.r(z) is the reference current,E(z) is the tracking error,y(z) is the output of the system,GC(z)is the PI controller.GP(z) is the controlled object, andGrc(z) is the repetitive controller.

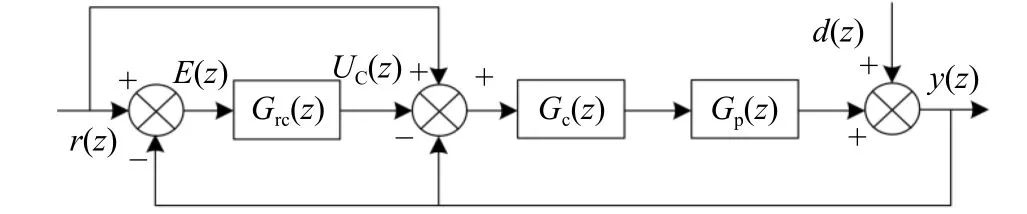
Fig. 4 Cascade compound repetitive control system

3.3 Repetitive Controller Parameter Design

The design of repetitive controller mainly includes three steps.

1) Design of low pass filterQ(z)：Q(z) is used to improve the critical stability characteristics of repetitive control internal model. The smaller the integral coefficient is, the more robust the system will be, but the worse the steady-state error accuracy will be. Besides, the larger the integral coefficient is, the smaller the steady-state error will be, and the better the output waveform quality of the system will be, but the system output will more likely be oscillatory. Generally, the value is less than 1 to improve system stability. In this paper, the integral coefficient is selected as 0.95.

2) The design of sampling timesN： the sampling period of the system isTs, and the fundamental wave period of the output sinusoidal voltage isT0. The period delay coefficient can then be obtained, that is, carrier ratioN=T0/Ts.In order to reduce odd harmonics better, –N/2 is selected here.

3) The design of repetitive control compensation linkC(z) in Eq. (6) can be carried out according to the following formula as

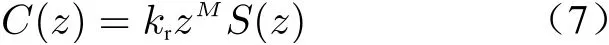
The gainkrof compensator is used to satisfy the amplitude compensation requirement of repetitive control. The gainkrof repetitive control was chosen as 0.9.

The low-pass filter is commonly used to eliminate the resonant peak, and thus reasonable parameter design needs to be performed such that, the filter is at the resonant frequency attenuation of –20 dB—–30 dB, which can meet the requirements of eliminating the resonant peak.H(z) is the feedback control transfer function before the repetitive controller is added to the system, it can be derived as

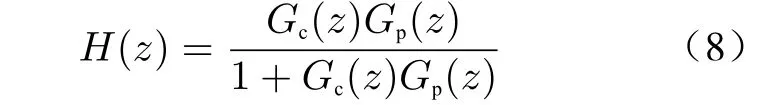
The resonant compensatorS(z) designed as the second-order filter to provide only high-frequency attenuation, such that the cut-off frequency of the second-order filter could be improved. The cut-off frequency of the low-pass filter is set as the resonant frequency of the controlled object, i.e., 1 kHz. The critical damping method is adopted, and the damping coefficient is 0.707.

Secondly, the lead compensationzMis determined. The lead compensation needs to be introduced to carry out phase compensation. Because repetitive control itself has a delay link, lead compensation link can be realized directly. The selection of thezMvalue is achieved by the Bode diagram method. The specific method is: draw the Bode diagram ofH(z)S(z), and then draw the Bode diagram ofzM. The selection ofMparameter can be completed through the comparative analysis of the phase lag characteristics between the modulez-Mand the compensation object in order to achieve the best phase compensation effect [26].

3.4 Stability Analysis of Repetitive Control System

withUc(z) being the command signal to the closed-loop system as shown in Fig. 4.

The output in Fig. 4 is

4 Simulation Verification and Analysis

Given the specific parameters, the discretized transfer function can be obtained as

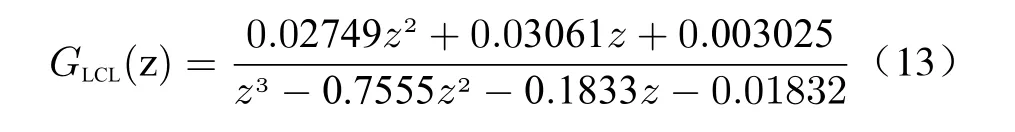
Tab. 1 System simulation parameters

PI controller is inserted before repetitive control to compensate for the slow dynamic response speed caused by the existence of delay link of repetitive control technology. After simulation verification, the proportional functionkp=30,ki=6.H(z) is the feedback control transfer function

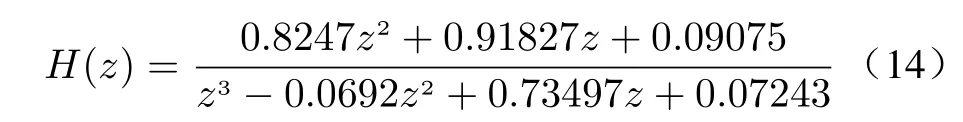
Line 1 in Fig. 5 shows the Bode diagram of the controlled objectH(z).

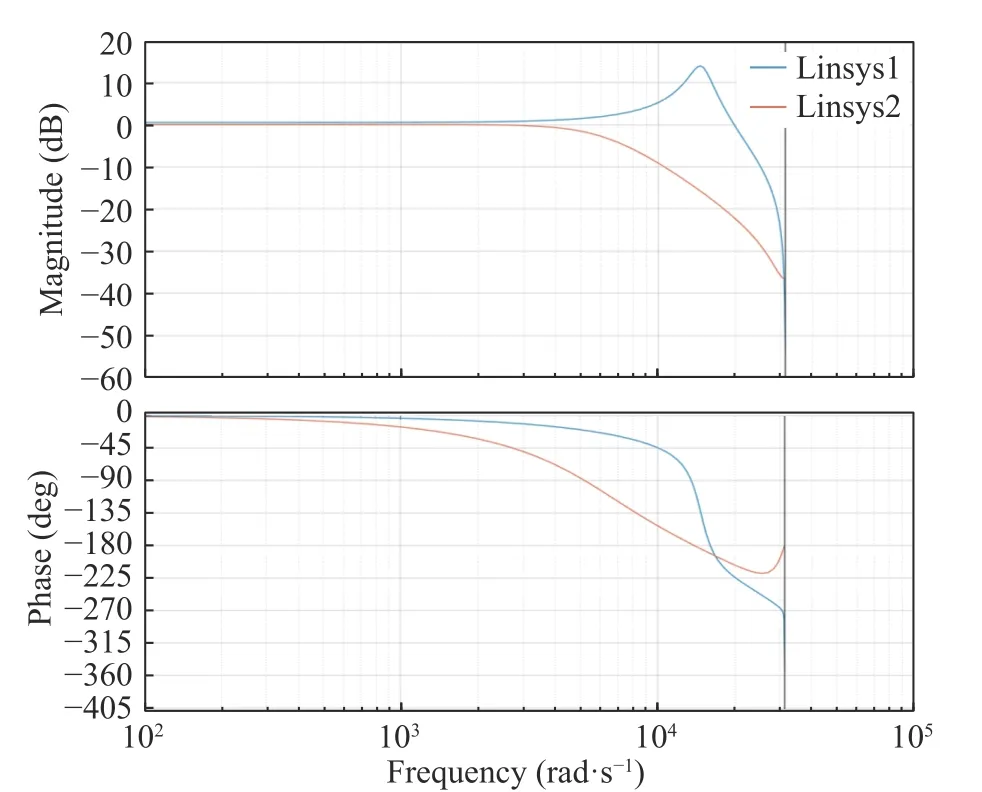
Fig. 5 Bode diagram for filter H(z) and S(z)

After discretization of the designed secondorder low-pass filter, the resonant compensatorS(z) can be obtained, and the Bode diagram of filterS(z) is shown in line 2 in Fig. 5.

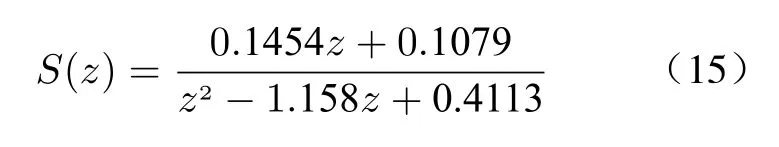
Fig. 6 is the compensation effect diagram of the lead compensation with different orders. The phase frequency characteristic curve ofz-4is almost completely coincident with the phase frequency characteristic curve of the control object in the middle and low frequency band. It can be considered that the lead compensation linkz4of four beats in advance can effectively compensate and correct the phase lag problem of the system,and ensure the control characteristics of zero phase shift in the middle and low frequencies of the system.

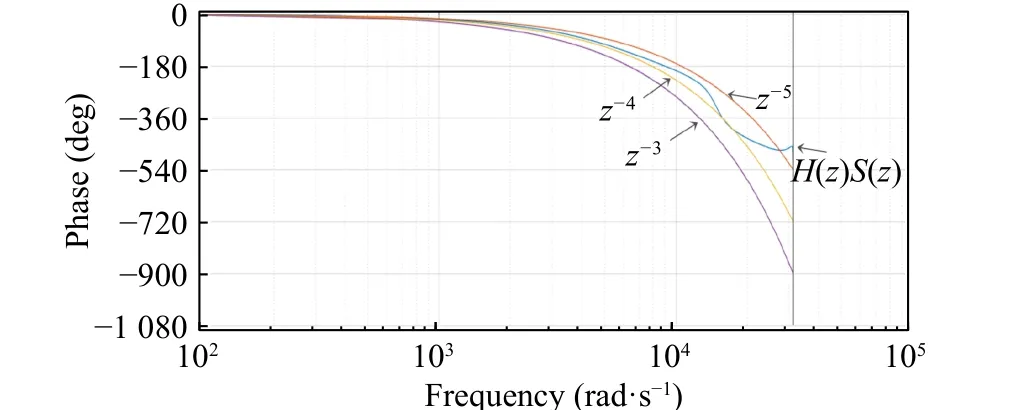
Fig. 6 Analysis on compensation effect of lead compensation zM

Given theTsandT0in this work,Nis equal to 10 000/50=200.

The root locus diagram of the control objectH(z) can then be drawn, and it can be seen that the inner loop system itself is stable. The root locus diagram is shown in Fig. 7.

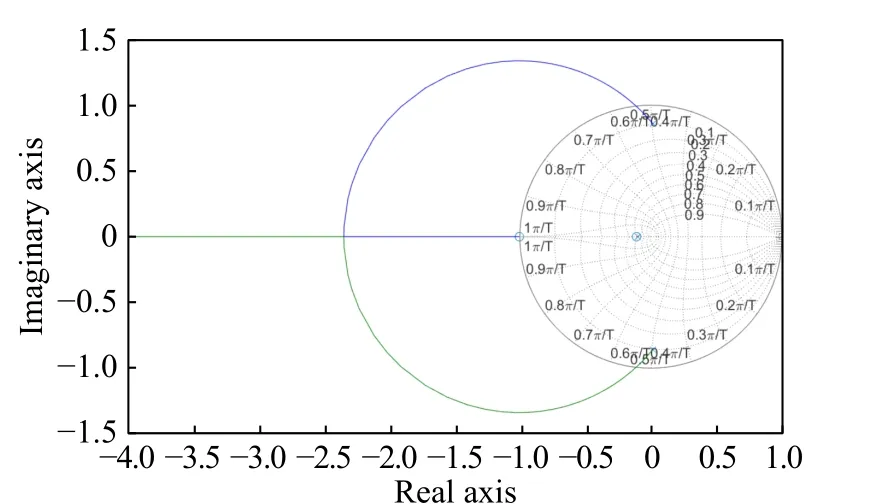
Fig. 7 Control object H(z) root trace diagram

In the following, the performance of the traditional PI control and the proposed repetitive control is discussed in detail.

4.1 Static Analysis

4.1.1 Experimental Waveform and Analysis

Using PI Control Scheme

The three-phase grid-connected voltage and current waveform is shown in Fig. 8. The current of axisdis shown in Fig. 9. The A-phase voltage and current waveform is shown in Fig. 10, and the PI control spectrum analysis is shown in Fig.11.

Fig. 8 Simulation waveform of grid-connected voltage and current under PI control: (a) voltage waveform; (b) current waveform

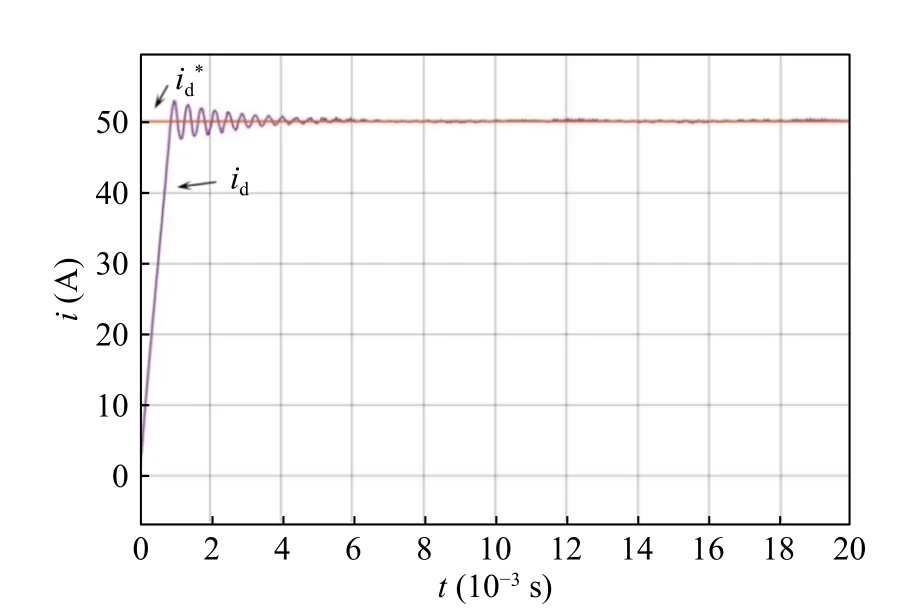
Fig. 9 D-axis current component tracking diagram

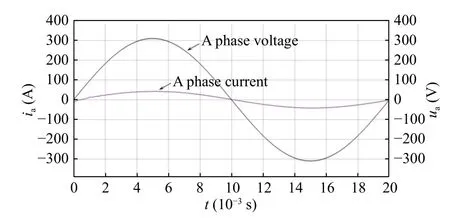
Fig. 10 A-phase grid-connected voltage-current simulation waveform under PI control

When only PI control is used, it can be seen from Fig. 8 and Fig. 10 that A-phase voltage and current are in the same phase and the current waveform has good sinusoidal property. As can be seen from Fig. 9, thed-axis current oscillation frequency is at a higher level, the transition time is longer, and the overshoot is larger, indicating that the tracking performance is poor. THD of grid-connected current under PI control is 0.74%and odd harmonic component is high in Fig. 11.

Fig. 11 PI controlled spectrum analysis

4.1.2 The Experimental Waveform Analysis

Using the Proposed Improved Compound Repetitive Control Scheme The three-phase grid-connected voltage and current waveform is shown in Fig. 12. The current of axisdis shown in Fig. 13. The A-phase voltage and current waveform is shown in Fig. 14,and the spectrum analysis of improved composite repetitive control is shown in Fig. 15.

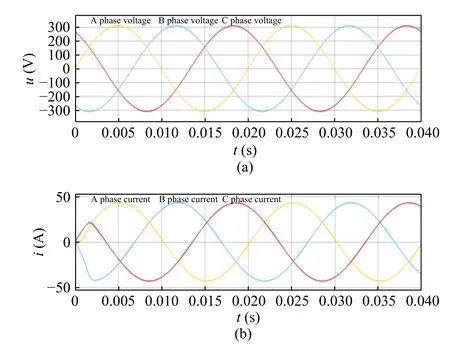
Fig. 12 Voltage-current simulation waveform under improved compound repetitive control: (a) voltage waveform;(b) current waveform

When using the improved compound repetitive control, as shown in Fig. 13，it is observed that thed-axis current oscillation, the transition time, and the overshoot all become smaller,which shows that the tracking performance is significantly improved. As can be seen from Fig. 12 and Fig. 14, A-phase voltage and current are in the same phase, and the current waveform has good sinusoidal property. It can be seen from Fig.15 that the grid-connected current THD under improved composite repetitive control is 0.57%.Odd harmonic component is low.

Fig. 14 A-phase voltage-current simulation waveform under improved compound repetitive control

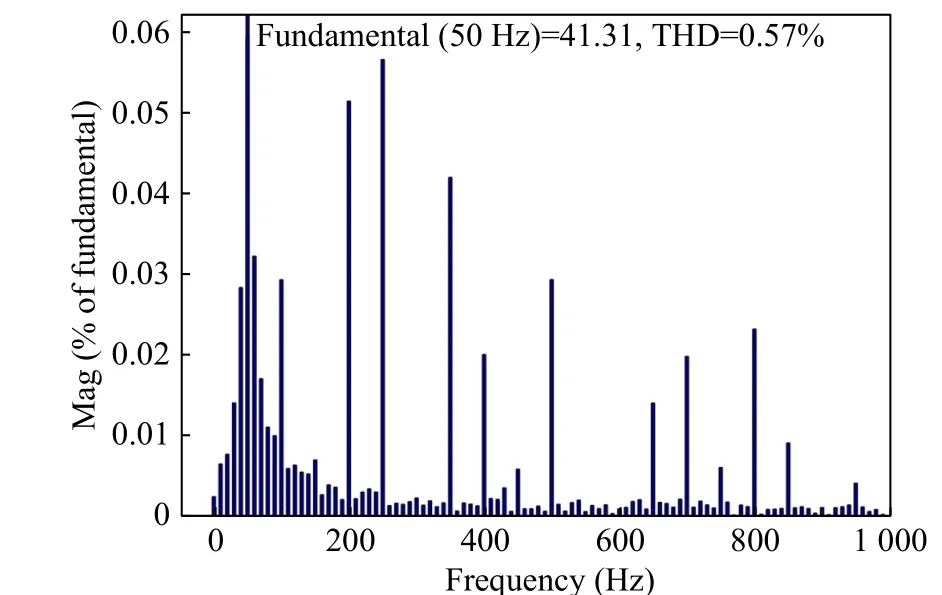
Fig. 15 Spectrum analysis of improved composite repetitive control

4.2 Dynamic Simulation

This section analyzes the dynamic performance under the reference current mutation. The mutation of grid-connected current and voltage under PI control current mutation is shown in Fig. 16.The mutation of grid-connected current and voltage under the control current mutation of compound repeat control is shown in Fig. 17.

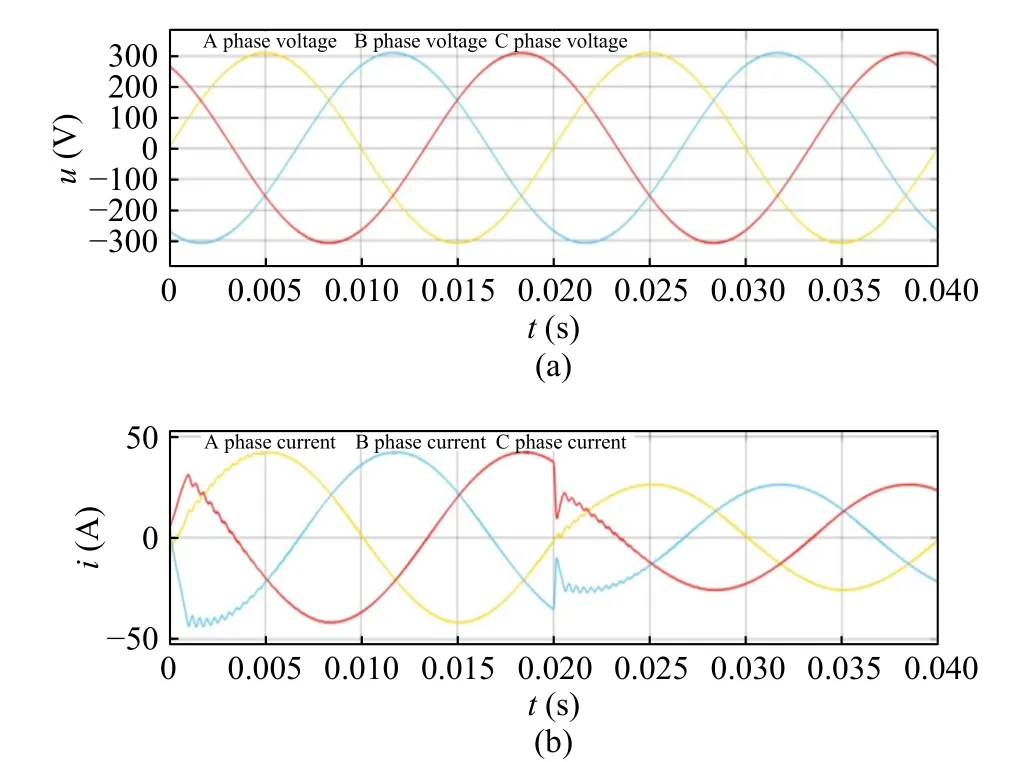
Fig. 16 PI controls the mutation of grid-connected current and voltage under the mutation of current: (a) voltage waveform; (b) current waveform

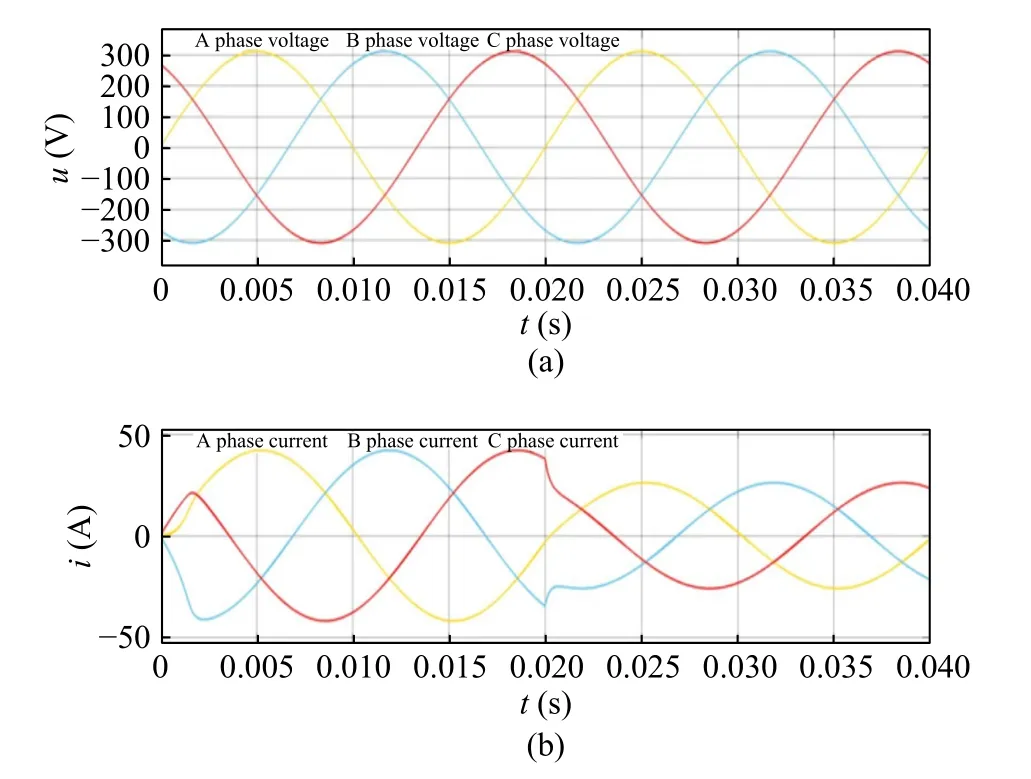
Fig. 17 Simulation waveform of grid-connected current and voltage mutation under compound repetitive control:(a) voltage waveform; (b) current waveform

It can be seen that the improved repetitive controller has faster system stability time than the PI controller, and the waveform of threephase current controlled by single PI is not as smooth as that of improved compound repetitive control.

Through the above simulation verifications,it can be seen that compared with the existing method, the improved compound repetitive controller proposed in this paper can achieve better steady and dynamic performance, which proves the effectiveness of the improved compound repetitive control.

5 Conclusion

Based on the mathematical modeling of LCL grid-connected inverter, the cascaded compound repetitive control strategy based on odd internal mode is proposed, and is further combined with PI control. The stability property of the proposed control scheme is analyzed, the stability condition is derived. compensator design method,and the advantages and disadvantages of the proposed control scheme are summarized. The simulation results show that the proposed compound scheme of repetitive control can effectively improve the odd harmonic suppression ability of LCL grid-connected inverter and obtain better incoming current waveform.

The future research is to perform an experimental analysis to validate the proposed repetitive control. In addition, since this paper only analyzes the control method combining repetitive control and PI control, we can try to study the utilization of other waveform control technologies to comprehensively improve the steadystate accuracy and dynamic performance of the considered system.