基于Johnson-Cook本构模型的高强度装甲钢动态力学性能参数标定及验证

张杜江， 赵振宇， 贺良， 任建伟， 强鹭升， 周贻来

(1.南京航空航天大学 机械结构力学及控制国家重点实验室， 江苏 南京 210016；2.南京航空航天大学 多功能轻量化材料与结构工业和信息化部重点实验室， 江苏 南京 210016；3.内蒙古第一机械集团有限公司 特种车辆及其传动系统智能制造国家重点实验室， 内蒙古 包头 014030)

0 引言

简易爆炸装置(IED)和地雷等爆炸物产生的爆炸冲击载荷严重威胁车辆乘员的生命安全，优化车体结构设计和选择先进装甲防护材料是提升车辆防护性能的主要措施，而车底防护结构的构型设计一旦确定，材料选择成为另一研究重点。在集中、均布等外部载荷作用下，Jones理论分析了理想刚塑性均质梁/板的动态响应，给出了其无量纲挠度与无量纲冲量之间的关系。从无量纲冲量的表达式中可以看出，选择屈服强度高的材料可降低无量纲冲量，从而降低均质板无量纲挠度，提升抗爆性能。随着我国军用装备的快速发展，对装甲钢的综合性能提出了更高的要求，某装甲钢具有较高的屈服强度(大于1 400 MPa)，为我国装甲车辆的防护结构设计提供了新的材料选择。

通常，采用大量试验对防护结构的构型或者材料选择进行验证，试验成本较大，研发周期也较长，而采用数值仿真技术先期进行分析和优化设计，可节约试验成本与时间。对防护结构的动态响应过程进行数值分析，首先需要确定结构所使用材料的本构模型及相关材料参数。其中，由于Johnson-Cook本构模型(以下简称J-C本构)考虑了金属材料的硬化效应、应变率效应和温度效应，并得到了充分的实验验证，在国内外实现了广泛应用。胡昌明等利用温度为25～300 ℃和应变率为10～10s的拉伸应力- 应变曲线，通过拟合获得了45号钢的J-C本构参数；郭子涛等研究了Q235钢在常温至900 ℃的准静态和动态压缩及拉伸力学性能，修正了J-C本构模型中的温度软化项，并利用Taylor撞击实验和数值仿真验证了其动态本构关系；Senthil等通过12.7 mm和7.62 mm穿甲燃烧弹侵彻20 mm厚的7075铝合金板，验证了获得的7075铝合金J-C本构参数；高玉龙等通过温度为-50～300 ℃的单轴拉伸试验、应变率为10～10s的单轴拉伸和压缩试验，使用试验和仿真相结合的方法，进行了0°剪切、45°剪切、单轴拉伸、单缺口拉伸和双缺口拉伸试验，得到了6008铝合金J-C本构的硬化及损伤断裂参数。基于实验测量，6008铝合金、7075铝合金、工业纯铁、304不锈钢、45号钢、Weldox 900E、Armox 500T、钛合金等典型金属材料的J-C本构参数如表1所示。此外，由于大型商业有限元软件(如Abaqus、LS-DYNA等)均内置了J-C本构，该本构已广泛应用于防爆结构设计、汽车耐撞性检验、飞机防鸟撞设计等领域。

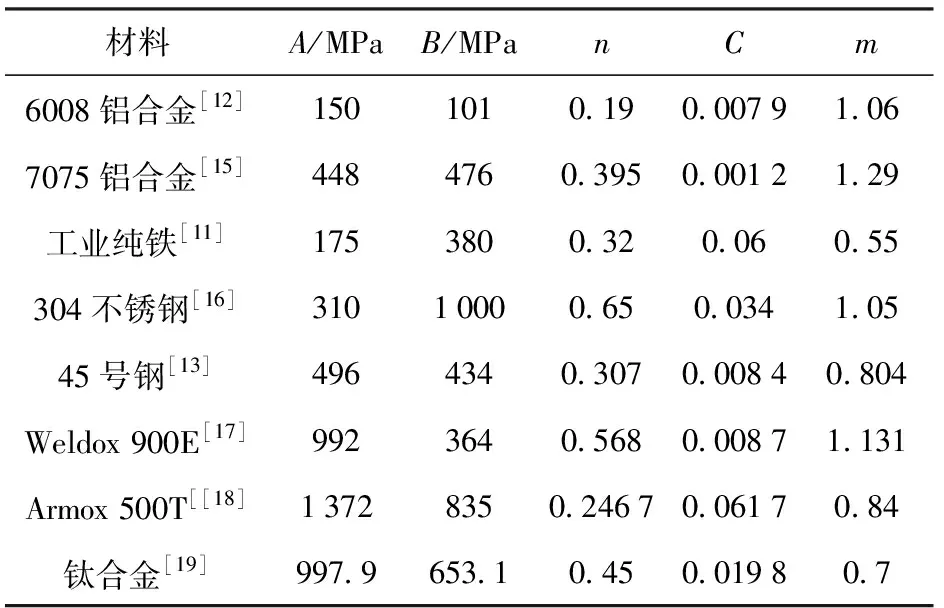
表1 典型金属材料的J-C本构模型参数

针对我国某装甲钢材料抗冲击力学性能及J-C本构模型参数的研究，目前未见公开报道。为准确模拟该装甲钢在爆炸载荷下的响应过程，获得其动态本构关系参数是必要的；一般而言，由于装甲车的防护结构设计应确保防护结构在炸药爆炸后不破裂，研究不涉及J-C本构模型的断裂参数。

本文在常温和高温环境下开展某装甲钢的准静态拉伸试验研究，同时在常温环境下，采用分离式霍普金森压杆测试系统开展不同应变率下的动态压缩试验研究。基于J-C本构模型并结合材料实验结果数据，拟合得到该装甲钢的J-C本构模型参数；再次，采用轻气炮和泡沫铝弹丸对该装甲钢均质梁开展冲击试验研究。分别采用J-C本构模型和理想弹塑性模型进行有限元仿真计算，并将数值结果与冲击试验进行对比分析。

1 本构模型

Johnson和Cook等基于材料各向同性假设，考虑材料的硬化效应、应变率效应和温度效应的影响，提出了著名的J-C本构模型。J-C本构模型将应力- 应变关系表示为

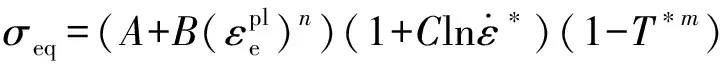
(1)

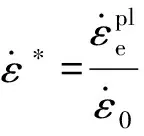
(2)

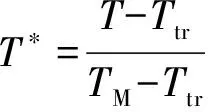
(3)

分别开展常温、高温条件下的准静态拉伸试验以及分离式霍普金森压杆试验研究，然后基于试验数据拟合获得某装甲钢的J-C本构模型参数，具体步骤如下：

1)常温条件下，开展准静态拉伸试验，根据获得的真实应力- 应变数据可得屈服强度。随后，考虑应变硬化系数和应变硬化指数，忽略应变率和温度的影响，此时(1)式可简化为

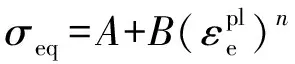
(4)

基于(4)式，对真实应力- 应变曲线塑性段进行数据拟合，可得应变硬化系数和应变硬化指数。

(5)

基于(5)式，对不同温度下获得的真实应力- 应变曲线，取多个相同塑性应变值的点进行拟合，得到多个热软化系数，然后取平均值。

3)考虑应变率对屈服应力影响时，无量纲温度为0，则应力和无量纲应变率的关系简化为

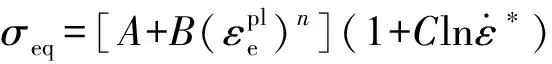
(6)

基于(6)式，对于不同应变率下获得的真实应力- 应变曲线，取多个相同塑性应变值的点进行拟合，得到多个应变率硬化系数，然后取平均值。

2 材料性能测试

2.1 常温下准静态性能试验

根据国家标准GB/T 228.1—2010金属材料拉伸试验第一部分室温试验方法，设计某装甲钢的拉伸试验样件，如图1所示。试验样件处于弹性拉伸阶段时，拉伸速率取为0.216 mm/min，此时应变率为1×10s；材料进入塑性拉伸阶段后，拉伸速率取为3 mm/min。图2给出室温为20 ℃时3次重复试验后得到的真实应力- 应变曲线。由图2可见，某装甲钢在室温条件下没有明显的屈服点。因此，选择试验样件产生0.2%塑性应变时的真实应力作为屈服强度，将3次试验得到的屈服应力进行平均，得到该装甲钢的屈服应力为1 458 MPa。同时，对图2中真实应力- 应变曲线的弹性阶段进行线性拟合，得到装甲钢的弹性模量为220 GPa。

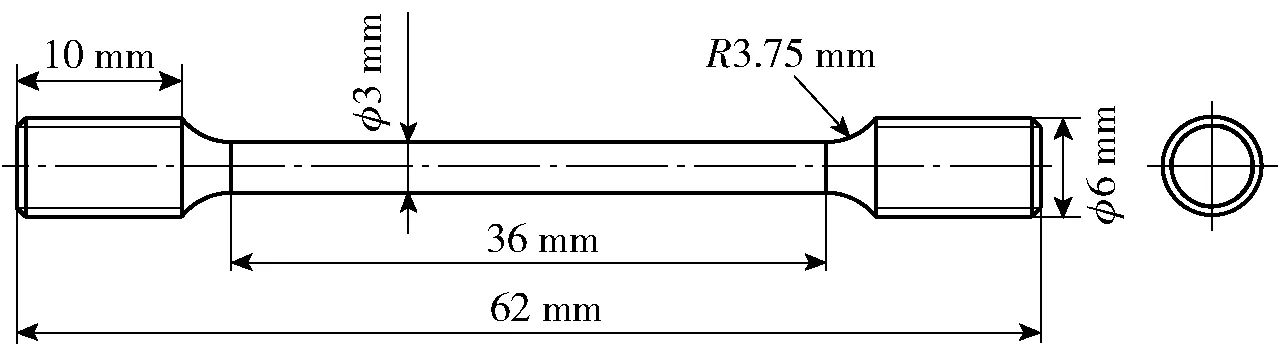
图1 拉伸试验样件尺寸Fig.1 Dimensions of tensile specimens

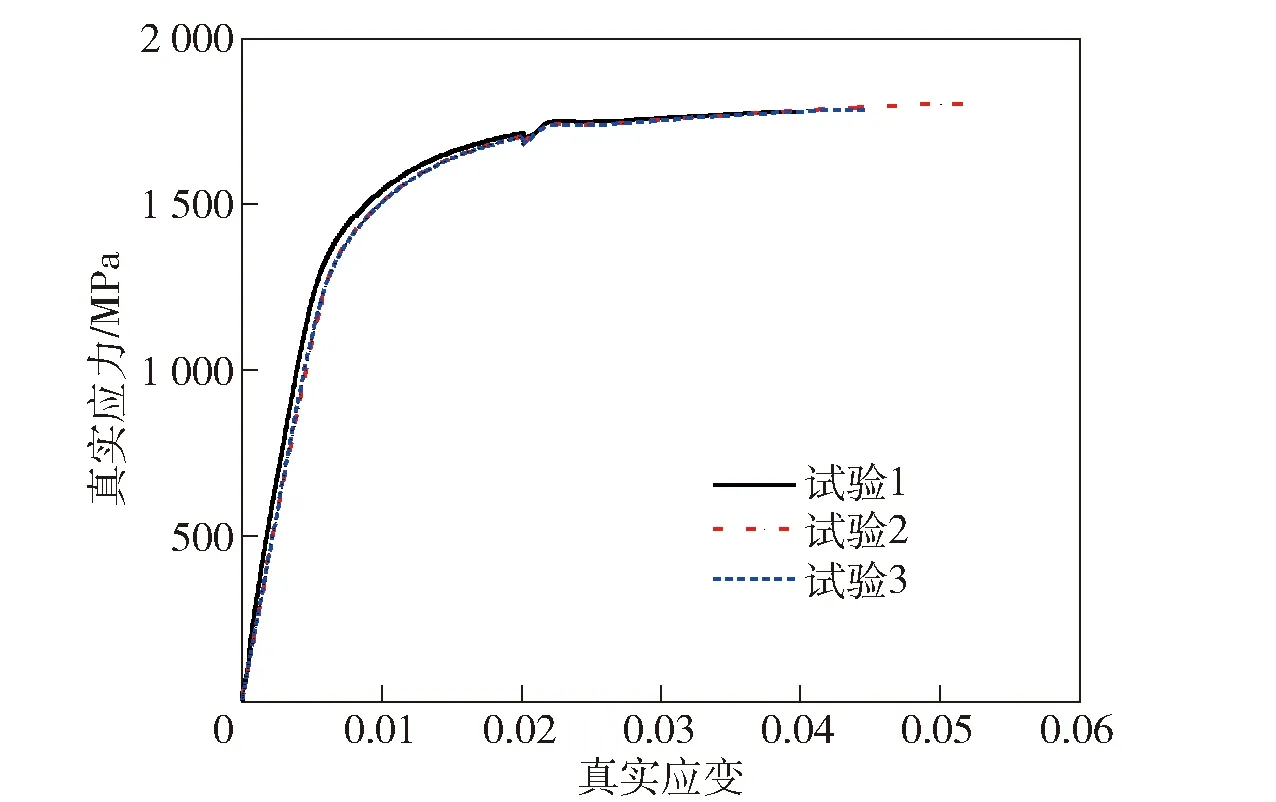
图2 室温(20 ℃)条件下真实应力- 应变曲线Fig.2 True stress versus true strain curve at room temperature (20 ℃)

2.2 高温下准静态性能试验

在温度为180 ℃、260 ℃、370 ℃和550 ℃条件下，对图1的试样进行3次准静态拉伸试验。图3给出了室温和高温条件下的真实应力- 应变曲线，图4所示为屈服强度随温度变化曲线图。由图3和图4可见：从室温20 ℃变为180 ℃时，屈服强度下降相对缓慢，温度为180 ℃时，流动应力没有出现通常认为的下降，而是流变应力大于室温时的流变应力，Wang等在2015年首次将这一现象命名为“第三型应变时效”，这是由运动位错与扩散的溶质原子的相互作用引起的。位错在障碍前等待时，溶质原子向位错扩散，在位错周围形成溶质原子气团，对运动位错“钉扎”，阻碍了位错的运动，在宏观上表现为金属流动应力增大。温度大于180 ℃时，该装甲钢的屈服强度明显降低，且呈线性下降，如图4所示。

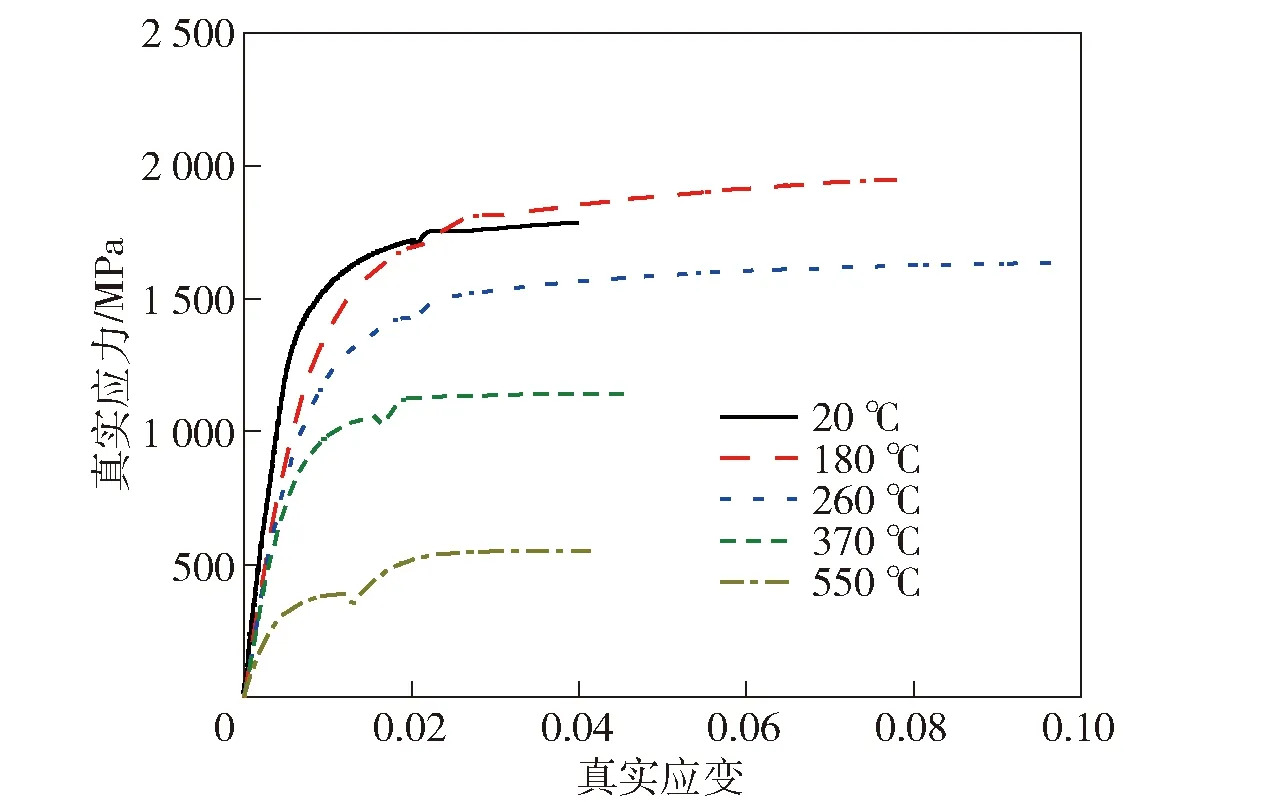
图3 不同温度下真实应力- 应变曲线Fig.3 True tress versus true strain curve at different temperatures

图4 屈服强度随温度变化曲线Fig.4 Yield stress versus temperature

2.3 动态性能测试

根据国家军用标准GJB 8799—2015金属材料动态压缩试验方法，采用尺寸为6 mm×5 mm的圆柱形样件，开展不同应变率下的分离式霍普金森压杆冲击试验，如图5所示。

图5 分离式霍普金森压杆试验样件Fig.5 Specimens for Split-Hipkinson pressure bar tests

图6给出了6种不同应变率下的动态压缩应力- 应变曲线，可见该装甲钢的动态屈服强度大于其准静态屈服强度，且随着无量纲应变率的增加而增大。

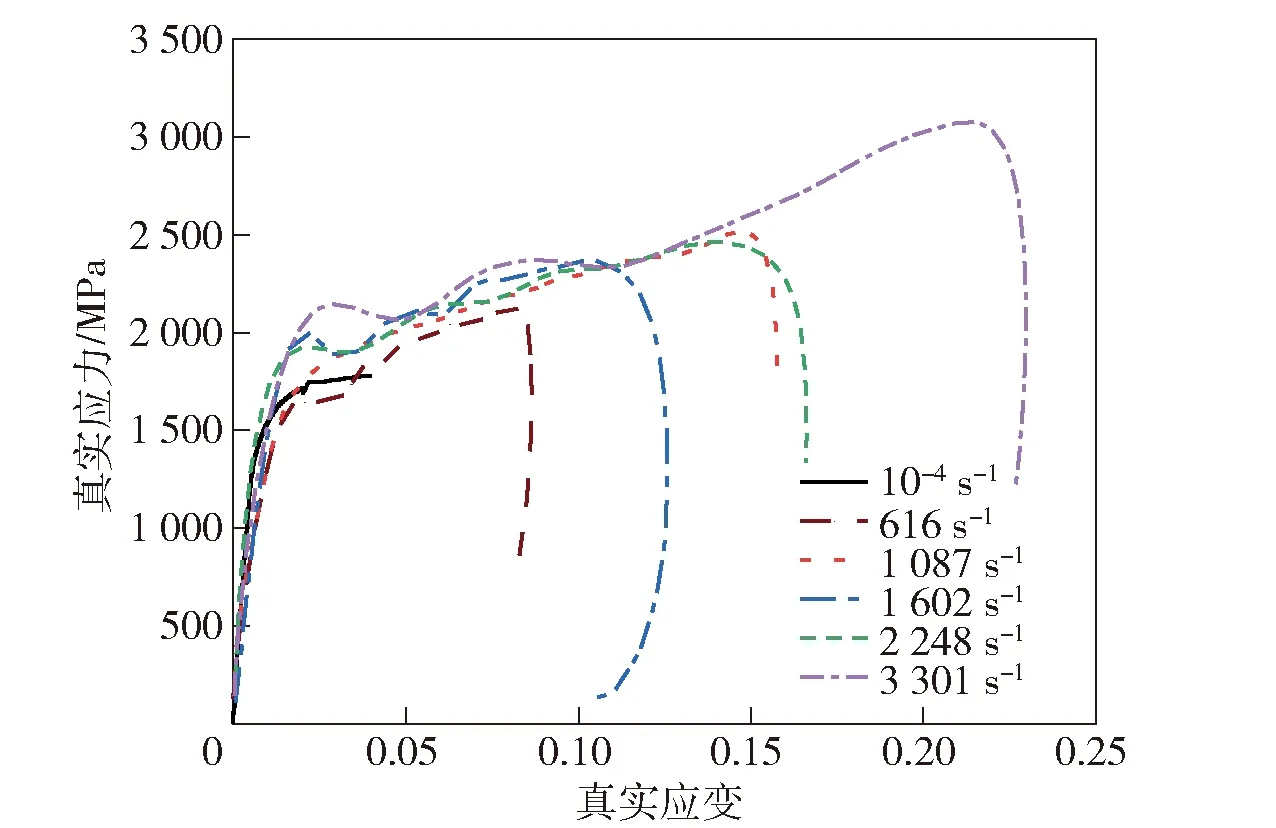
图6 不同应变率下真实应力- 应变曲线图Fig.6 True stress versus strain curves at different strain rates

3 参数拟合

采用(4)式对准静态真实应力- 应变曲线的塑性阶段进行拟合，如图7所示，拟合结果与试验数据吻合较好，由此得应变硬化系数为1 408 MPa，应变硬化指数为0.405。

图7 真实应力随塑性应变变化曲线Fig.7 True stress versus plastic strain

根据(5)式，对塑性应变为0、0.005、0.010、0.015、0.020、0.025和0.030时的应力和无量纲温度进行拟合，得到热软化参数分别为0.558、0.632、0.672、0.714、0.705、0.697、0.689，平均后为0.667。图8给出了塑性应变为0和0.030时，应力随无量纲温度变化曲线。

图8 应力随无量纲温度变化趋势Fig.8 Stress versus dimensionless temperature

根据(6)式，对塑性应变为0、0.005、0.010、0.015、0.020、0.025和0.030时的应力和无量纲应变率进行拟合，得到热软化参数分别为0.014 0、0.007 2、0.006 1、0.005 6、0.005 4、0.005 4、0.005 5，平均后为0.007。图9给出了塑性应变为0和0.030时，应力随对数应变率变化曲线。

图9 应力随对数应变率的变化趋势Fig.9 Stress versus log strain rate

综上所述，某装甲钢的J-C本构模型参数列入表2。

表2 某装甲钢J-C本构模型参数

4 材料参数验证

4.1 试验装置与样件

一级轻气炮冲击试验装置主要由支撑底座、压气室、炮筒、测试舱、回收舱及高速摄影机组成，如图10所示。由图10可见；在压气室中充入具有一定压力的氮气，高压气体释放后，泡沫铝弹丸受到高压气体作用，在炮管中加速并获得一定的初速度后冲击靶板(某装甲钢均质梁)；采用线切割工艺从闭孔泡沫铝上切出直径为58 mm，长度为100 mm的弹丸。图11所示为测试舱中工装夹具示意图，当泡沫铝弹丸运动到测试舱时，通过高速摄影机捕捉弹丸的运动过程和均质梁的响应过程。如图12所示，均质梁的长度2=370 mm，宽度2=60 mm，名义厚度=5 mm (实测为5.13 mm)。试验时，采用尼龙66扎带将均质板样件固定在夹具上。考虑到尼龙66的抗拉强度约为71.5 MPa，而扎带的横截面积较小，为1.3 mm×4.7 mm，经计算得到扎带断裂的临界载荷约为0.43 kN。由于临界载荷较低，在仿真时忽略尼龙扎带的影响。试验结束后，通过高速摄影机拍摄到的照片测量样件的变形过程，并测量样件的残余挠度。

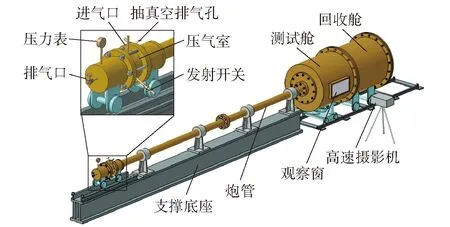
图10 轻气炮冲击试验装置Fig.10 Schematic diagram of the impact test setup

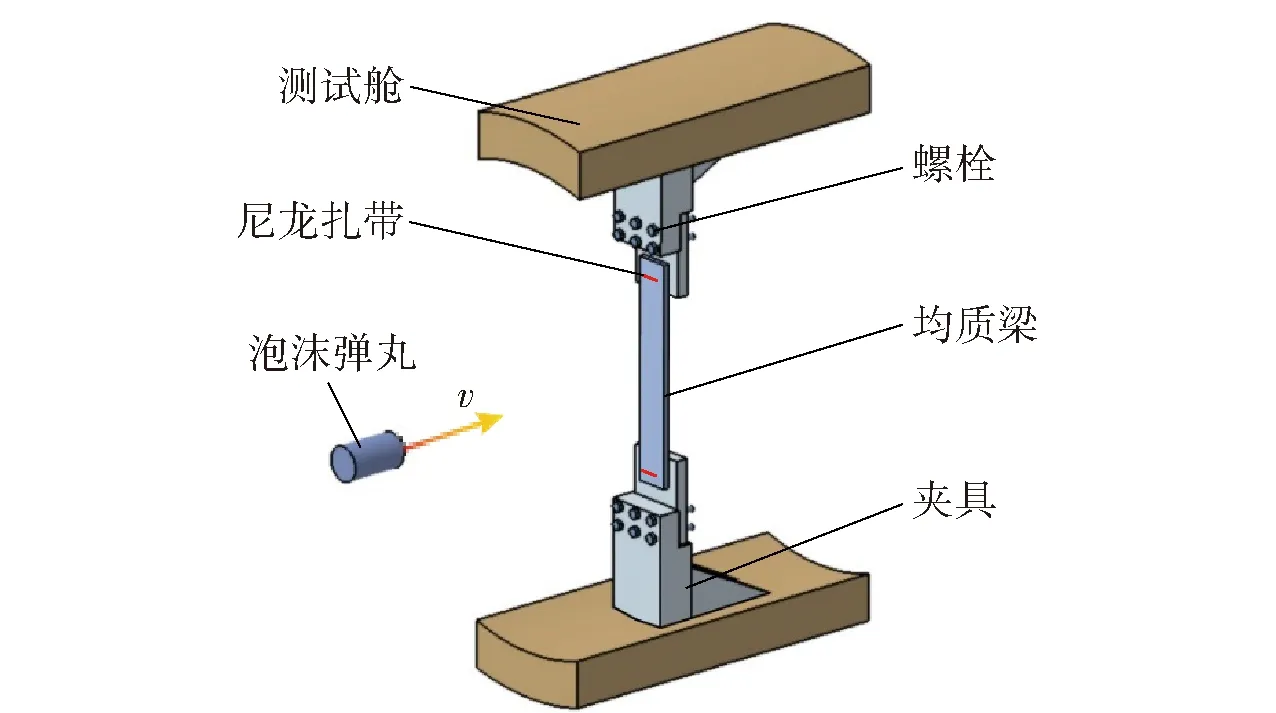
图11 测试舱内的试样及工装夹具Fig.11 Schematic diagram of beam specimen fixed in the test cabin

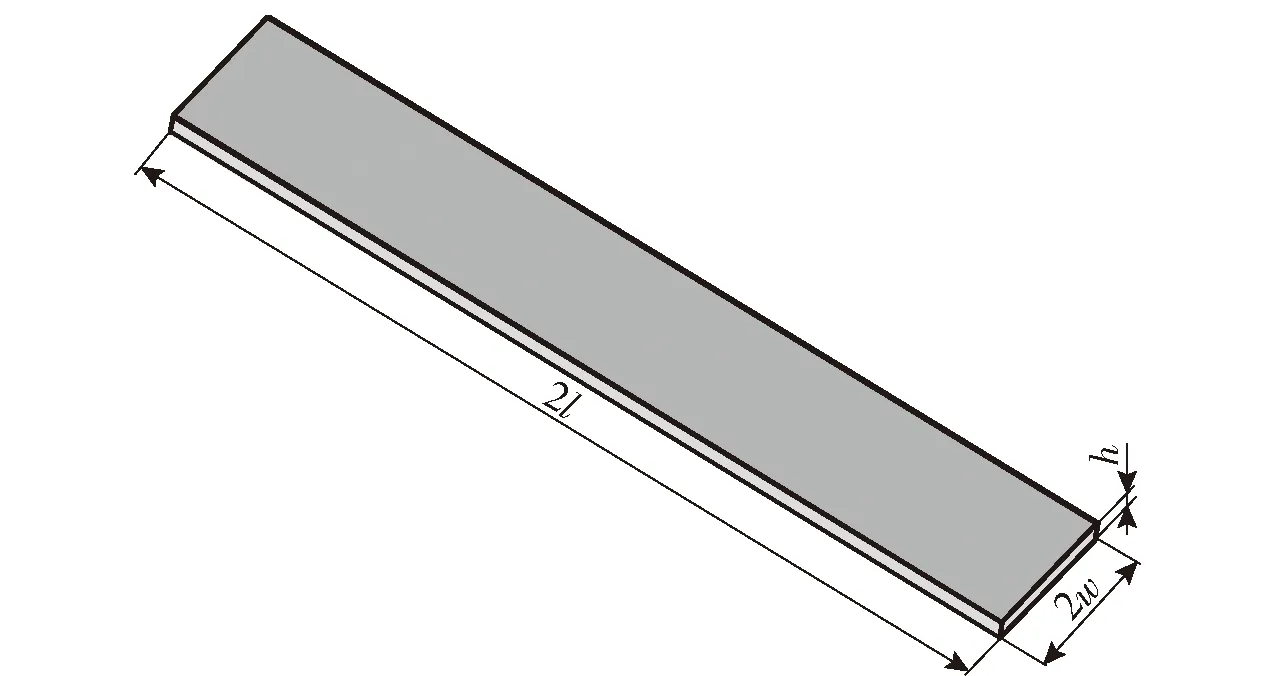
图12 某装甲钢均质梁样件示意图Fig.12 Geometry and dimensions of the monolithic beam made of the studied armor steel

为了在后续的仿真分析中模拟泡沫铝弹丸，开展了闭孔泡沫铝(密度370 kg/m)准静态单轴压缩试验，样件直径20 mm、高度50 mm，试验时的名义应变率为1×10s；图13给出了实测的工程应力- 应变曲线。图13中，为泡沫铝的名义致密应变，为平台应力。

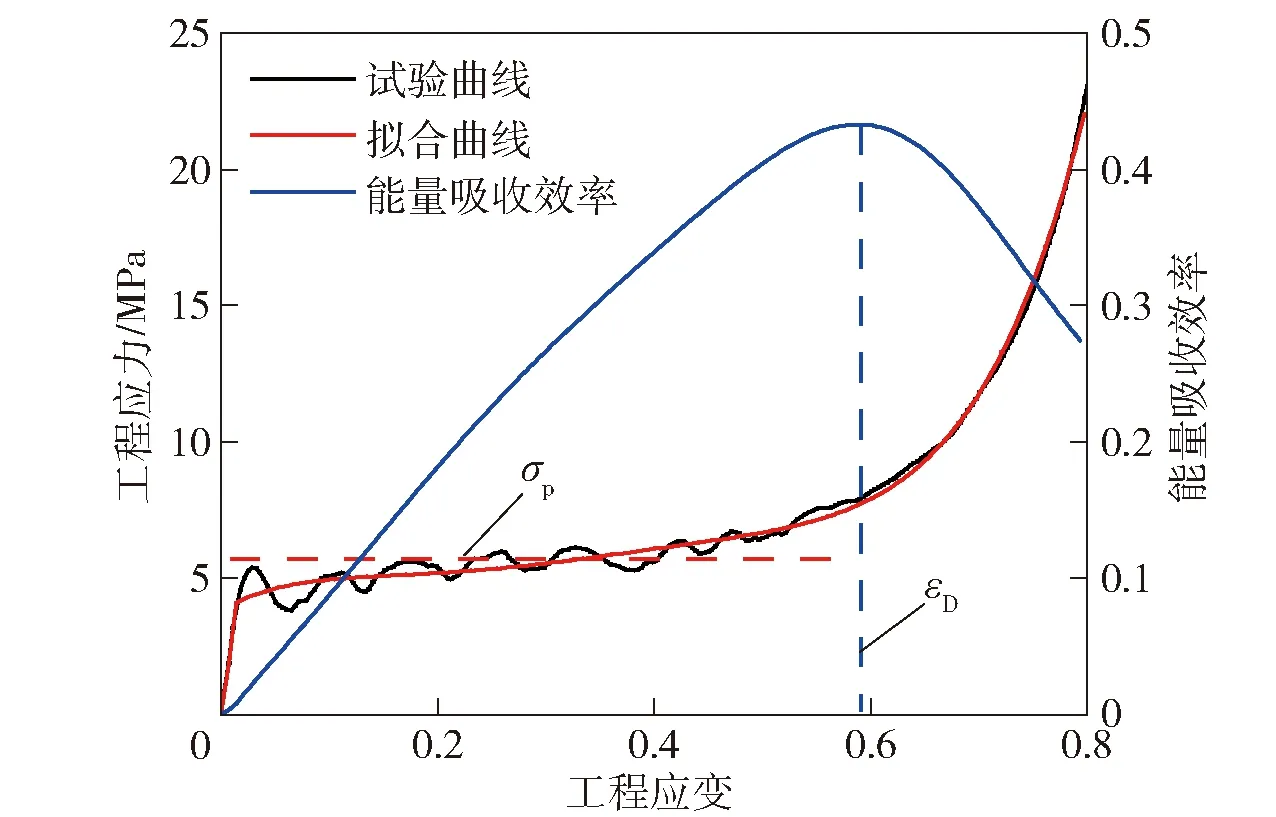
图13 单轴压缩下闭孔泡沫铝工程应力和能量吸收率随工程应变变化曲线Fig.13 Uniaxial compressive engineering stress and energy absorption efficiency versus engineering strain curve of closed-cell aluminum foam

为确定，定义能量效率参数如下：

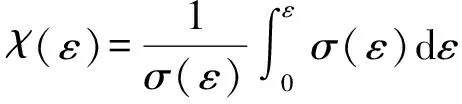
(7)

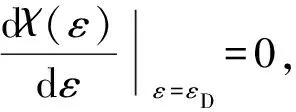
(8)

对图13的工程应力- 应变曲线进行多项式拟合，根据(7)式和(8)式确定能量效率曲线，可得=059，=57 MPa。

4.2 有限元模型

基于轻气炮冲击试验，采用有限元软件Abaqus对泡沫铝弹丸冲击均质梁的过程进行数值模拟。图14给出的有限元模型包括泡沫铝弹丸、某装甲钢均质梁和固支的工装夹具。其中，均质梁长度为370 mm，宽度为60 mm，厚度为5.13 mm(试验样件的实际厚度)。为避免弹丸和均质梁之间在冲击初始即出现网格穿透，建模时在弹丸和均质梁之间设置厚度为0.1 mm的间隙。为避免在后续计算过程中出现网格穿透，在有限元模型中设置通用接触；均质梁和完全固定的工装夹具之间的摩擦系数取为0.3。采用Crushable Foam本构模拟泡沫铝：根据单轴压缩下闭孔泡沫铝工程应力- 应变变化曲线中的弹性阶段进行线性拟合，拟合得到的斜率为泡沫铝弹性模量，大小为210 MPa；由于泡沫铝的塑性泊松比为0，体积应变=()=，其中为准静态压缩工程应变，为泡沫铝的初始高度，为泡沫铝的初始横截面积，因此准静态压缩工程应变与体积应变是相等的，本构中的应力- 体积应变关系由图13中数据给出。Deshpande等通过霍普金森压杆试验得到了泡沫铝在不同应变率下的应力应变曲线，结果表明泡沫铝对应变率的变化不敏感，高华等研究了多次冲击下泡沫铝的动态压缩力学性能。在Radford等、Wang等、Yu等研究泡沫弹丸冲击三明治梁的过程中，用准静态应力- 应变曲线和Crushable Foam本构模型描述泡沫铝的动态冲击行为。因此，在仿真分析时忽略了泡沫铝的应变率效应，并使用Crushable Foam本构模拟泡沫铝。

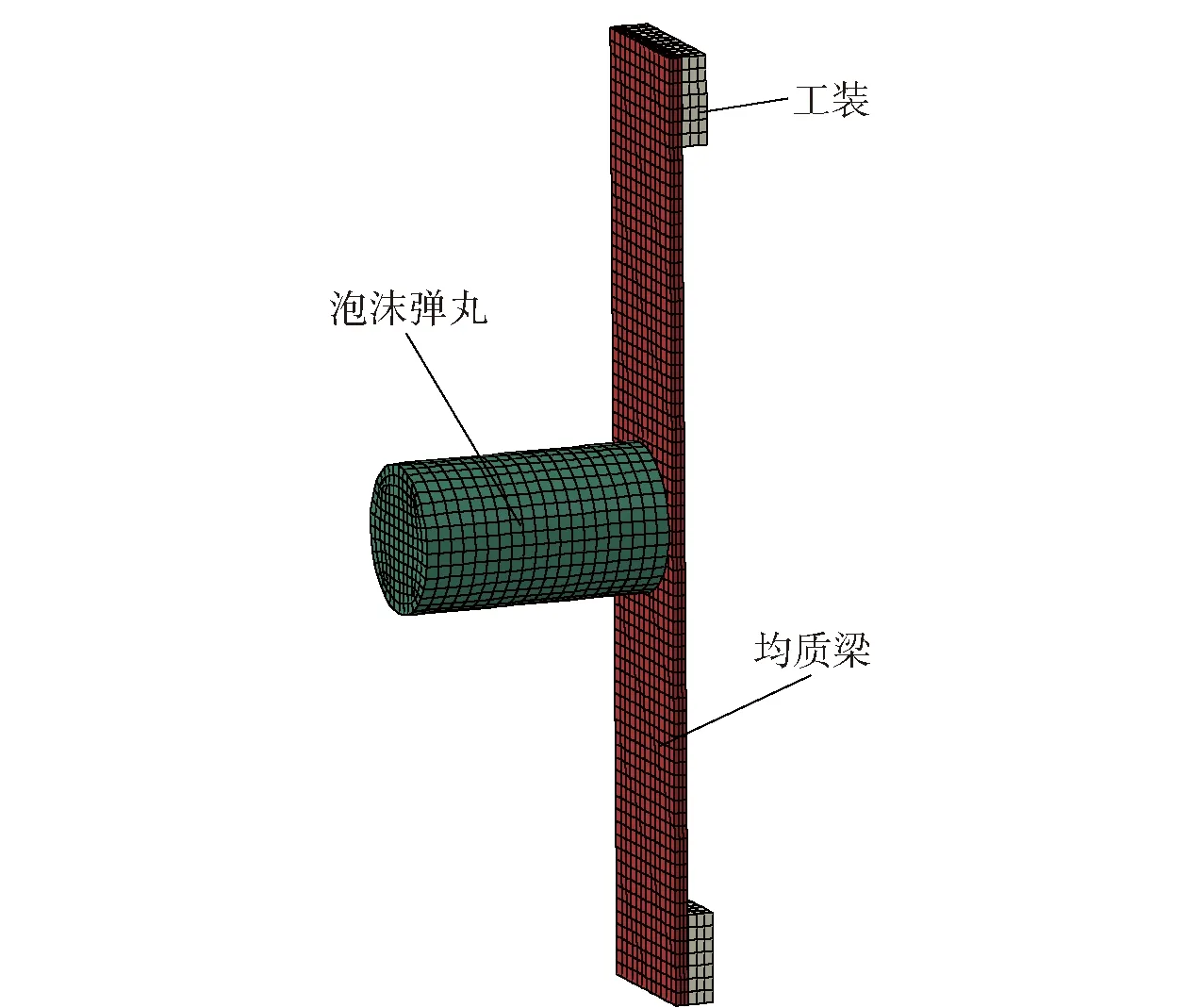
图14 泡沫弹丸冲击某装甲钢均质梁有限元模型Fig.14 Finite element model of the monolithic armor steel beam subjected to foam projectile impact

为得到有限元模拟的最优网格尺寸，首先进行网格无关性分析。采用C3D8R实体网格划分均质梁和泡沫铝弹丸，均质梁在厚度方向分为3层网格，每层厚1.71 mm，在面内方向，网格尺寸大小依次取2 mm、3 mm、4 mm、5 mm、6 mm、7 mm、8 mm；对泡沫铝弹丸的网格做相应划分。图15给出了泡沫铝弹丸冲量=8.0 kPa·s时均质梁无量纲中点峰值挠度和无量纲残余挠度随网格尺寸的变化趋势，其中，无量纲中点峰值挠度等于中点峰值挠度除以梁长度的一半，无量纲残余挠度等于残余挠度除以梁长度的一半；其他冲量下的变化趋势类似，故不重复给出。当网格尺寸为2 mm时，无量纲中点峰值挠度和无量纲残余挠度趋于稳定，并且与试验值相接近。因此，选择尺寸为2 mm的网格进行后续分析。此外，为比较不同本构模型对均质梁动态力学响应的影响，分别采用J-C本构模型和理想弹塑性本构模型对某装甲钢进行了仿真模拟。

图15 均质梁无量纲中点峰值挠度和无量纲残余挠度随网格尺寸变化趋势(I=8.0 kPa·s)Fig.15 Midpoint peak displacement and residual deflection of the monolithic beam versus mesh size (I=8.0 kPa·s)

4.3 结果与讨论

表3给出了3次重复实验条件下泡沫铝弹丸冲击均质梁的试验与仿真结果对比。由表3可见：中点峰值挠度和残余挠度的试验和仿真结果吻合较好，相对误差全部小于10%；随着弹丸冲量的增加，峰值挠度和残余挠度都有所增加，但试验后的泡沫铝名义应变基本不变。表3结果表明，获得的某装甲钢J-C本构参数是可靠的。

表3 泡沫铝弹丸冲击均质梁的试验与仿真结果对比

图16给出了冲量为8.0 kPa·s的弹丸冲击作用下均质梁的变形过程。由图16可见：弹丸高速撞击均质梁的前2 ms，泡沫铝剧烈压缩，均质梁获得速度并与弹丸一起向右运动；=3.9 ms时，弹丸与均质梁中点运动到最大挠度处，二者此时的中点速度均为0 m/s，均质梁中存储的弹性能最大；>3.9 ms期间，均质梁中存储的弹性能释放后转化为均质梁和弹丸的动能，二者获得向左的速度，开始反向运动(即回弹)。图17给出了试验结束后泡沫铝弹丸的最终形貌。表3对比了泡沫铝弹丸名义应变的试验和仿真结果，相对误差在10%左右。根据图16的高速摄影照片，可对均质梁的动态响应过程做出定性分析。下文结合有限元计算结果进一步分析。

图16 泡沫铝弹丸冲量I=8.0 kPa·s时均质梁动态变形过程Fig.16 Dynamic deformation of the monolithic beam subjected to an impact impulse of I=8.0 kPa·s

图17 试验后的泡沫铝弹丸最终形貌Fig.17 Final profiles of the aluminum foam projectiles after tests

冲量为8.0 kPa·s条件下，图18对比了无量纲中点挠度试验和仿真结果随时间变化的曲线，图19给出了相应的无量纲挠度随时间变化曲线。图18表明无量纲中点挠度的试验结果和基于J-C本构模型的仿真结果总体吻合较好：前1.5 ms时，试验和仿真曲线完全重合；>1.5 ms时，有限元结果略低于试验结果，但变化趋势相同；=3.9 ms时，试验和仿真结果同时到达峰值，随后出现下降(即均质梁反向运动，见图16)。基于J-C本构的仿真结果与试验结果的相对误差为1.7%；相比较而言，基于理想弹塑性本构的计算结果与试验值得偏离较大，相对误差为12.2%。图19表明，冲击载荷下，均质梁的无量纲挠度先增后降，再升高、降低，呈现周期振动。取振动时的平衡位置作为残余挠度，则基于 J-C本构模型的仿真结果与试验结果的相对误差为7.6%，而基于理想弹塑性本构模型的仿真与试验结果的相对误差为46.4%。相对于J-C本构模型，理想弹塑性本构模型无强化阶段，故采用该本构模型进行仿真的误差较大。

图18 均质梁无量纲中点峰值挠度随时间变化曲线(I=8.0 kPa·s)Fig.18 Midpoint displacement of the monolithic beam versus time (I=8.0 kPa·s)

图19 均质梁无量纲挠度随时间变化曲线(I=8.0 kPa·s)Fig.19 Deflection of the monolithic beam versus time (I=8.0 kPa·s)

基于J-C本构模型进一步开展仿真计算，分析泡沫铝弹丸和均质梁系统中的能量转化。在泡沫铝弹丸冲量=8.0 kPa·s冲击载荷下，图20给出了系统中的总能量、总应变能、总动能、黏性耗散能和摩擦耗散能；图21所示为不同能量占总能量的百分比随时间变化曲线；图22给出了弹丸和均质梁的动能和塑性耗散能随时间变化曲线；图23所示为弹丸和均质梁的动能和塑性耗散能占总能量的百分比随时间变化曲线；图24展示了均质梁在泡沫铝弹丸冲击下的变形过程。由图20～图24可见：=0 ms时刻，系统和弹丸的总动能最大，其他能量为0 J；0<<0.4 ms，弹丸的动能急剧下降，均质梁的动能有所上升(见图22)，但系统的总动能急剧下降，主要转化为弹丸和均质梁的应变能、弹丸的黏性耗散能(见图20)，变形模式上表现为泡沫铝的急剧压缩(见图24(a)～图24(c))；=0.4 ms时刻，泡沫铝压缩完毕，黏性耗散能不再变化；0.7 ms<<3.9 ms，均质梁的动能开始下降，转化为均质梁的弹性能和塑性耗散能，均质梁出现塑性变形(见图22)；=3.9 ms时刻，均质梁的动能最低，其中点挠度达到最大(见图24(g))；>3.9 ms，均质梁中存储的弹性能转化为弹丸和均质梁的动能，二者开始反向运动(见图24(g)～图24(i))。

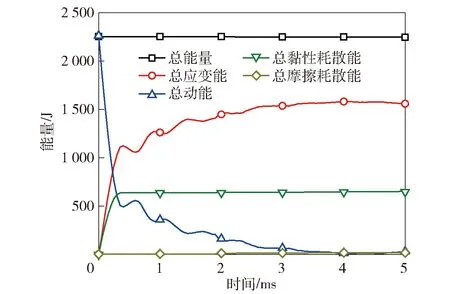
图20 系统中总应变能、总动能、黏性耗散能和摩擦耗散能随时间变化的曲线(I=8.0 kPa·s)Fig.20 Total strain energy， kinetic energy， viscous dissipation energy and frictional dissipation energy in the system versus time (I=8.0 kPa·s)

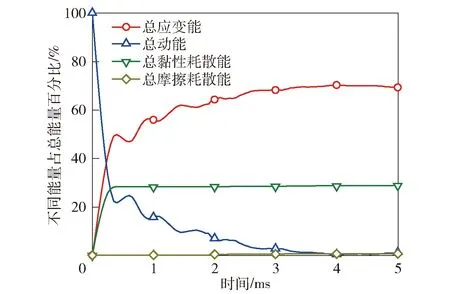
图21 不同能量占总能量的百分比随时间变化曲线 (I=8.0 kPa·s)Fig.21 Proportions of various energy versus time (I=8.0 kPa·s)

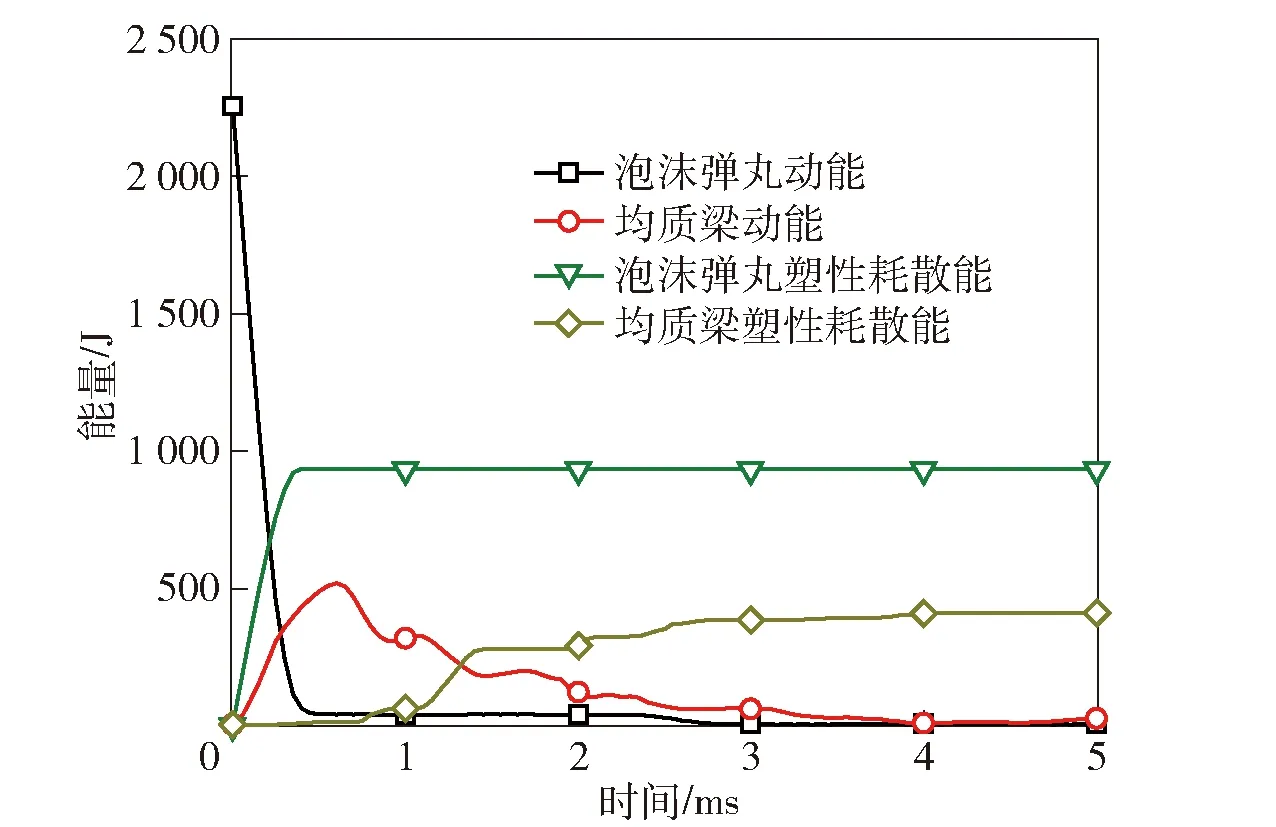
图22 弹丸和均质梁的动能和塑性耗散能随时间变化曲线 (I=8.0 kPa·s)Fig.22 Kinetic energy and plastic dissipation energy of foam projectile as well as monolithic beam versus time (I=8.0 kPa·s)

图23 弹丸和均质梁的动能和塑性耗散能占总能量的百分比随时间变化曲线(I=8.0 kPa·s)Fig.23 Percentage of kinetic energy and plastic dissipation energy of foam projectile as well as monolithic beam versus time (I=8.0 kPa·s)

图24 泡沫铝弹丸冲击下的均质梁变形过程(I=8.0 kPa·s)Fig.24 Numerically predicted deformation process of the monolithic beam subjected to foam projectile impact (I=8.0 kPa·s)

图21表明：0 ms<<3.9 ms期间，系统的动能在系统总能量中的占比逐渐减低，应变能和黏性耗散能的占比则升高；>3.9 ms期间，应变能中的弹性能和动能之间存在相互转化，梁和弹丸获得向左运动的速度；=5 ms时，系统总应变能占比为69.3%，黏性耗散能占比29.1%，总动能占比1.1%，摩擦耗散能的占比仅为0.7%。图23表明，=5 ms时，泡沫铝弹丸的塑性耗散能占比为41.6%，加上其黏性耗散能占比28.9%，弹丸的总耗散能为70.5%，均质梁的塑性耗散能占比则为18.2%。

5 结论

为准确模拟具有高屈服强度的某装甲钢的动态力学行为，本文基于J-C本构模型通过常温和高温环境下的准静态拉伸实验数据，以及常温环境下的动态压缩实验数据，拟合得到了J-C本构参数；随后采用轻气炮和泡沫铝弹丸对该装甲钢均质梁开展冲击试验研究，同时分别采用J-C本构模型和理想弹塑性本构模型进行有限元仿真计算，并对比分析了试验与数值仿真结果。结果表明：某装甲钢具有应变率强化效应，温度软化效应显著；采用J-C本构模型仿真的均质梁峰值挠度与试验结果的相对误差为1.7%～6.1%，残余挠度相对误差为0.6%～7.6%。