Al/Ni粉末复合材料冲击反应细观机制
2022-08-27熊玮张先锋陈海华刘闯谈梦婷
熊玮, 张先锋, 陈海华, 刘闯, 谈梦婷
(南京理工大学 机械工程学院, 江苏 南京 210094)
0 引言
Al/Ni材料是典型的含能结构材料,通常采用粉末压制法制备[1-2],同时具备结构特性和化学反应释能特性。该类材料在一般情况下保持惰性且不相互反应,当给予足够的机械、电或激光等刺激后会迅速释放大量的化学能,进行快速燃烧或爆炸[3]。由于兼具含能和强度特性,含能结构材料在军事领域和民用领域均具有十分广阔的应用前景[4-8],如制作含能破片、含能药型罩、基于含能结构材料的侵彻体及空间碎片防护结构等。
活性材料冲击释能行为中包含的力- 热- 化学耦合问题十分复杂[9]。在冲击压缩或强动载情况下,含能结构材料中将发生塑性变形、微射流、破碎及微孔塌陷等过程,因此冲击波阵面后将发生材料颗粒的迅速混合,最终引起温度的升高及材料内各组分的融合而发生化学反应[10-11]。含能结构材料冲击引起的化学反应过程可以分为3步:反应的触发、传播与扩展[10]。Al/Ni材料属于复合材料,在冲击压缩过程中的化学反应类型主要为多组分固相反应。文献[12]研究结果表明,Al/Ni粉末复合材料的细观结构(颗粒尺寸、形状以及颗粒分布等)对其力学行为及冲击反应特性的影响十分显著。由冲击压缩引起的含能结构材料细观/微观尺度上颗粒碰撞与变形、物质输运、温度分布、化学反应的发生与发展及材料动力学特性(密度、压力、冲击波等)如何影响宏观尺度的冲击反应特性参数(反应速率、反应效率及反应温度)是准确预测含能结构材料在冲击载荷下的力学行为和化学反应特性的关键问题之一。
由于含能结构材料的冲击释能特性较难通过商业有限元软件中已有的材料模型进行描述,使其研究工作主要集中于含能结构材料力学响应和冲击反应行为试验及含能毁伤元对典型目标毁伤效果的试验验证上[13-15]。虽然国外学者在含能结构材料的冲击反应细观模拟上已开展了大量的研究工作,但是其采用的RAVEN代码目前仅在美国部分机构使用[16-18],无法得到推广。国内相关学者[19-21]利用Powder Burn、Lee-Tarver模型和LS-DYNA软件自定义本构模型等方法,对活性材料毁伤元、活性防护结构等作用过程进行了数值仿真计算。以上研究工作是对含能毁伤元冲击反应行为宏观数值模拟方法的初步探索,且未考虑材料细观结构对宏观冲击动力学响应和宏观反应行为的影响。鉴于此,以国内外通用的仿真软件为平台,开展含能结构材料的冲击反应过程细观模拟研究,获取冲击响应和冲击反应特性宏观参数是现阶段亟待解决的问题。
基于以上研究背景,本文结合Mie-Grüneisen状态方程和反应扩散模型描述Al/Ni粉末复合材料冲击压缩力学响应及化学反应行为。在细观尺度上计算Al/Ni粉末复合材料中冲击反应演化过程,分析冲击加载条件对冲击反应行为的影响规律,阐明化学反应对材料内温度和冲击压力的影响机制。本文建立的考虑冲击反应特性的含能结构材料冲击响应特性计算方法对于阐明含能结构材料冲击释能机制有重要意义,同时将有助于推动该类材料的设计和工程化应用。
1 Al/Ni粉末复合材料的细观结构及冲击释能特性
选用纯度≥99.5%的原料粉末制备试件,Al粉颗粒目数为600目(粒径<23 μm),Ni粉颗粒目数为200目(粒径<75 μm)。从图1中原始粉末及其扫描电子显微镜(SEM)照片可以观测到:Al粉颜色为浅灰色,细观颗粒为光滑的球形;Ni粉颜色为深灰色,细观颗粒为树枝状结构。文献[22]研究结果表明,化学计量比相等的Al、Ni粉末混合物在无氧环境下的化学反应特性最好。因此,根据该材料配比对Al、Ni粉末进行混合,并使用粉末压制法(见图2)制备Al/Ni粉末复合材料。该过程所采用压制压力为850 MPa,并保压至少2 min,尽可能减小压力卸载后试件回弹变形。在Al/Ni粉末复合材料压制过程中,对每个试件尺寸进行测量,以保证密度等满足设计要求,离散度控制在±2%以内。

图1 Al、Ni粉末及其细观结构照片Fig.1 Images and microstructures of Al and Ni powder
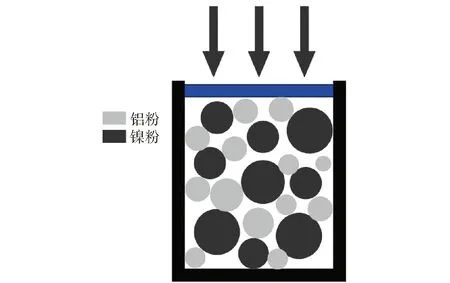
图2 粉末压制示意图Fig.2 Schematic image of the powder compaction process
通过上述方法得到的Al/Ni粉末复合材料理论密度为5.25 g/cm3,密实度为92.9%,其照片及细观结构如图3所示。由图3可以发现,通过粉末压制法得到的Al/Ni复合材料试件表面光滑,有金属光泽。Al、Ni颗粒在压制过程中发生了变形并相互结合在一起,Al-Al、Ni-Ni颗粒无明显分界。同时,根据文献[23]研究工作,Al/Ni粉末复合材料制备中未形成氧化层或金属间化合物,故不考虑氧化层对反应的影响。

图3 Al/Ni粉末复合材料及其细观照片Fig.3 Image and microstructure of the Al/Ni composite
根据文献[23]开展的准密闭容器二次撞击反应试验,测试Al/Ni粉末复合材料的冲击释能特性,结果如表1所示。由于试验中破片发生完全破碎或化学反应,导致试件无法回收,从而无法对反应产物进行分析。但是,可以通过试验中测得的化学反应释放量对反应情况间接分析。结果表明,在433~672 m/s的粒子速度下,Al/Ni粉末复合材料释放的化学能随着粒子速度的增大而提升。其中,当粒子速度低于433 m/s时,材料未发生化学反应。

表1 Al/Ni粉末复合材料冲击释能特性[23]
2 冲击反应细观模拟方法
2.1 细观几何模型的建立
为深入研究含能结构材料在冲击压缩过程中的物质输运过程和化学反应行为,采用细观模拟手段开展相关研究工作。由于本文所制备的Al/Ni粉末复合材料密实度较高,无法通过细观结构照片统计其孔隙尺寸及分布规律,因此为了建模方便将其近似为一种准密实材料。同时,为了反映Al/Ni粉末复合材料真实的细观结构特性,利用SEM照片建立细观几何模型,建模过程如图4所示。首先,将细观结构照片矢量化,使之成为能够通过具体数学方法描述的点、线及多线段。其中,SEM照片的放大倍数和所选区域必须能反映材料颗粒的分布规律和配比,从而保证由此得到细观仿真模型的有效性。通常,SEM拍摄的区域有限而不足以模拟整个冲击压缩过程中材料细观尺度上的变形行为及冲击波传播规律,因此需要采用适当的方法获取尺寸更大的细观模型。由图3可知,Al/Ni粉末复合材料的各材料颗粒形状分布具有随机性,即该材料的细观结构具有各向同性的特性。将所得到的矢量图沿x轴方向进行镜像处理,最终得到细观几何模型的截面尺寸为1.0 mm×0.4 mm。

图4 细观仿真模型建立过程Fig.4 Work flow for establishing the mesoscale model
为准确描述Al-Ni界面处的物质扩散及化学反应过程,冲击反应扩散模型将采用Lagrange算法。采用六面体网格(C3D8R)对几何模型进行划分,网格平均尺寸为2 μm,其局部示意图如图4(d)所示。为了模拟冲击波在Al/Ni粉末复合材料截面中的一维传播过程并减少计算时间,模型厚度方向尺寸取为一个网格大小。在细观模型的左侧建立刚性板,网格大小与细观模型一致。刚性板以恒定速度对细观结构进行压缩,材料中的粒子速度up即为刚性板的压缩速度。此外,为了模拟理想周期性材料细观结构和一维压缩条件,避免边界冲击波反射、稀疏波干扰等因素的影响,在除加载面以外的各个面均添加对称边界条件。
2.2 基本假设及冲击物态方程
当应力波幅值远超过材料的动态屈服强度时,与静水压应力分量相比,可以忽略剪切应力。因此可以认为材料进入了高压状态。对于固体来说,必须区别偏应力和静水应力。当前者较小,可将其忽略并应用流体的处理方法。因此,本模型的建立基于以下4点假设[25]:
1) 在高压状态将材料视为无黏性的可压缩流体,即材料的剪切模量为0 Pa;
2) 将材料本构简化为静水压力p与比容ν的关系,即固体高压状态方程;
3) 冲击波阵面上的体力(如重力)和热传导可以忽略;
4) 将冲击压缩过程视为冲击绝热过程,不考虑热量的耗散。
Al、Ni的冲击响应行为由Mie-Grüneisen状态方程[26]描述,该方程是常用的一种描述固体在冲击波高压条件下行为的物态方程,被广泛地使用来描述材料冲击压缩后的状态。其表达式为
p-pH=γρ(E-EH)
(1)
式中:pH和EH分别为Hugoniot压力和比内能;γ为Grüneisen参数;ρ为材料密度。
材料的冲击波速度us与粒子速度间[27]的关系采用线性形式[25]表示:
us=c0+Sup
(2)
式中:c0是材料声速;S是材料常数。材料参数如表2所示。表2中,M为该组元的摩尔质量,Cp为材料的定压比热容,λT为导热系数。

表2 冲击物态方程参数
2.3 冲击反应扩散模型
在冲击压缩过程中,若Al、Ni两相界面处满足化学反应阈值条件,将发生化学反应,生成化学反应产物。假设后续化学反应的发生基于如下两个过程:
1) 材料颗粒剧烈变形。材料内部初始阶段未接触的Al、Ni颗粒开始接触,并在达到化学反应阈值条件时发生反应。
2) 材料颗粒间的物质输运过程。材料界面处发生化学反应后,反应物能穿过反应产物进入另一种反应物中,在两种反应物达到反应阈值条件时发生化学反应。
为了阐明以Al/Ni粉末复合材料为代表的多相含能结构材料冲击反应机理,本文将结合以上两个过程建立考虑该类材料细观结构特性的数值模拟方法,重点关注细观尺度上Al、Ni两相间的化学反应过程。
2.3.1 物质扩散模型
任何非均质(包括成分、结构)的材料,在热力学条件允许的条件下,都将趋向于均匀化。固态中的扩散本质是在扩散力(浓度、电场、应力场等梯度)作用下,原子定向、宏观的迁移,最终导致系统的化学自由焓下降[28]。非稳态扩散过程通常用Fick第二定律进行描述:
(3)
式中:x、y、z为空间坐标系坐标值;D为扩散系数,
D=D0exp (-Ed/RuT)
(4)
D0为扩散系数的指前因子,取为0.05 m2/s,Ed为扩散活化能,取值为28 kJ/mol[29],Ru为摩尔气体常数,取值为8.314 J/(mol·K),T为温度;C为浓度,
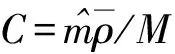
(5)
2.3.2 反应动力学模型
为了简化计算过程,假设本文所研究化学反应为一级反应过程,且不考虑各组分与空气之间的反应,即Al和Ni反应直接生成最终化学反应产物NiAl:
Ni+Al→NiAl
(6)
固态物质反应率常数可以采用Arrhenius方程的形式进行描述:
(7)
式中:A为指前因子;Ea为表观活化能,取值分别为5×109(mol·m-3)-1·s-1和88.6 kJ/mol[29]。
化学反应速率R[30]可以表示为
(8)
式中:CAl和CNi分别为反应物Al和Ni物质的量浓度。
各反应物和反应产物的物质的量浓度在反应发展过程满足:
(9)
式中:CNiAl为反应产物NiAl物质的量浓度。
2.3.3 反应扩散模型
在以Al/Ni粉末复合材料为代表的含能结构材料中,整个反应过程由扩散和相变反应两步组成。在此过程中,材料系统始终遵守质量守恒定律,即物质浓度的变化率等于浓度梯度引起的浓度变化率与化学反应引起的浓度变化率之和[28]:
(10)
式中:CK为组元K物质的量浓度,K=Al, Ni。
(10)式一维形式为
(11)
在物质扩散模型中,通常只考虑单向扩散过程,即只考虑扩散所需活化能Ed更小的过程[29-30]。由于材料Al向Ni中扩散的活化能大于Ni向Al中扩散活化能的两倍[29],因此本文仅考虑Ni向Al中扩散的过程。
由此得到各组元的物质的量浓度为
(12)

(13)

(14)
2.4 冲击反应扩散模型计算流程
冲击反应扩散模型的计算流程如图5所示,图中Δv、Δp、ΔT、ΔE、ΔTr、ΔEr分别表示该时间步下单元体积、密度、温度、内能及化学反应引起的温度和内能变化量,xi0、yi0分别为材料点i在x轴和y轴方向的坐标,Vol%为组元的体积分数。该计算过程可以分为3步:冲击压缩响应计算、反应扩散过程计算、温度及比内能更新。
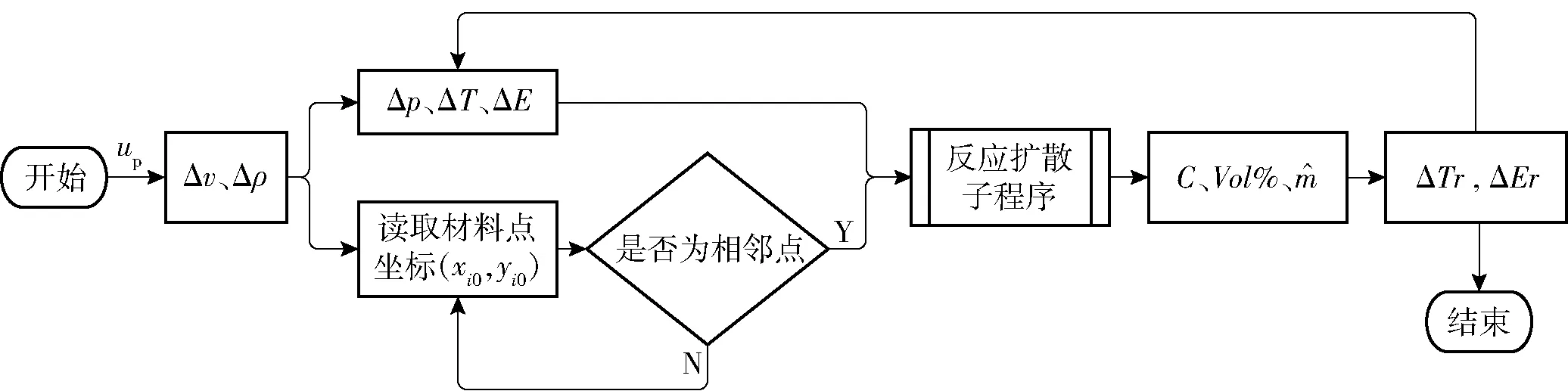
图5 冲击反应扩散模型计算流程图Fig.5 Flow chart for calculating the diffusion and chemical reaction process
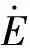
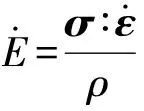
(15)
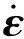
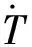
(16)
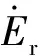
(17)
(18)
式中:QR为单位质量反应物完全反应所释放的化学能;NiAl为NiAl的质量分数。
3 冲击反应细观机制与分析讨论
3.1 不同粒径下的反应扩散结果初步分析
为了分析颗粒尺寸对冲击反应结果的影响规律,基于一维反应扩散方程(11)式对10 μm、20 μm、50 μm和75 μm 4种典型粒径下Al、Ni颗粒间的反应扩散情况进行计算。在1 000 K的温度下,将相互接触的Al、Ni颗粒加热0.2 μs,由(11)式可以得到不同位置各物质的浓度,进一步通过(5)式可以得到相应位置各物质的质量百分数,如图6所示。
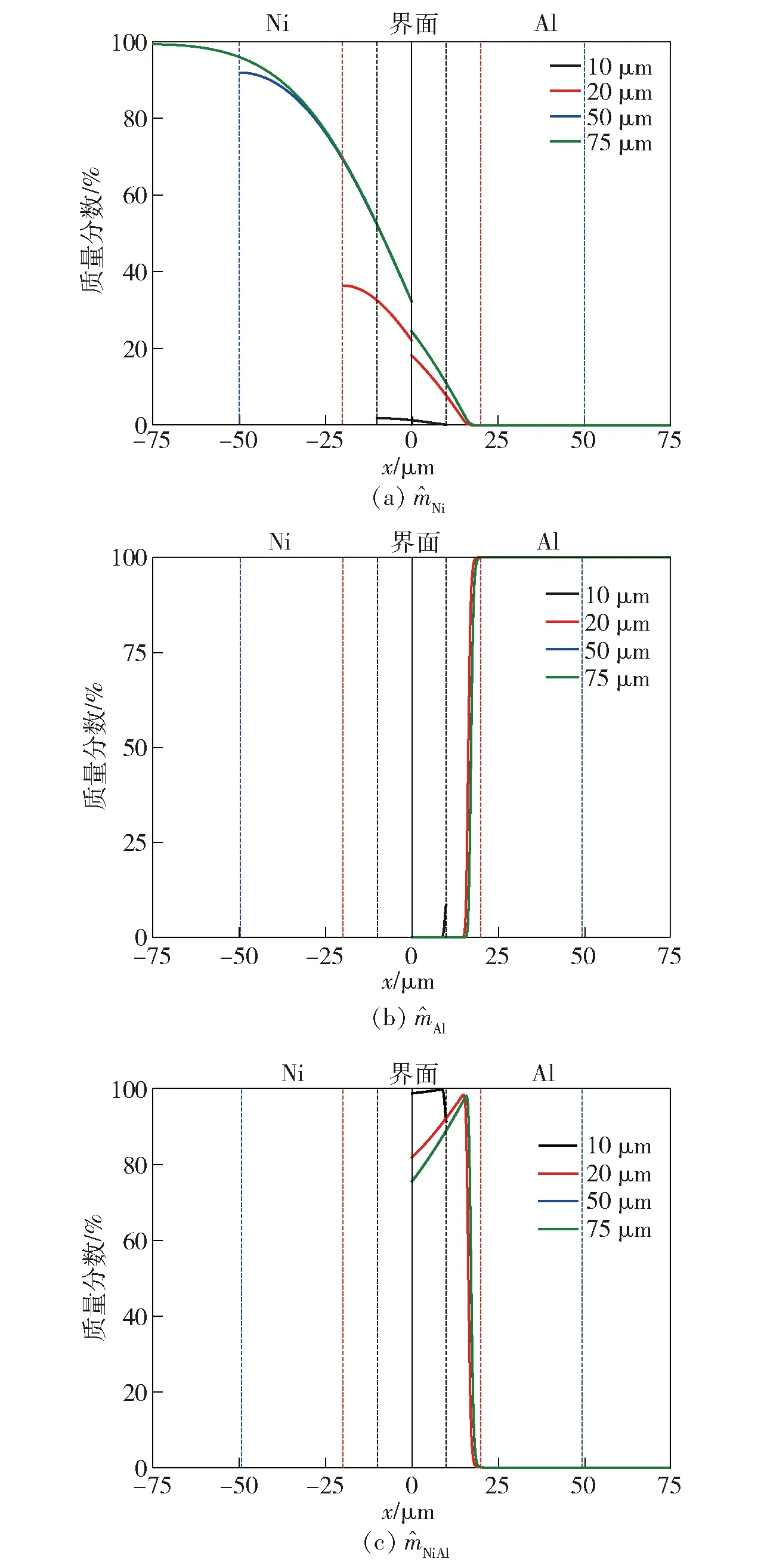
图6 不同粒径下Al、Ni颗粒间的反应扩散结果Fig.6 Results of reaction diffusion between Al and Ni with different particle sizes
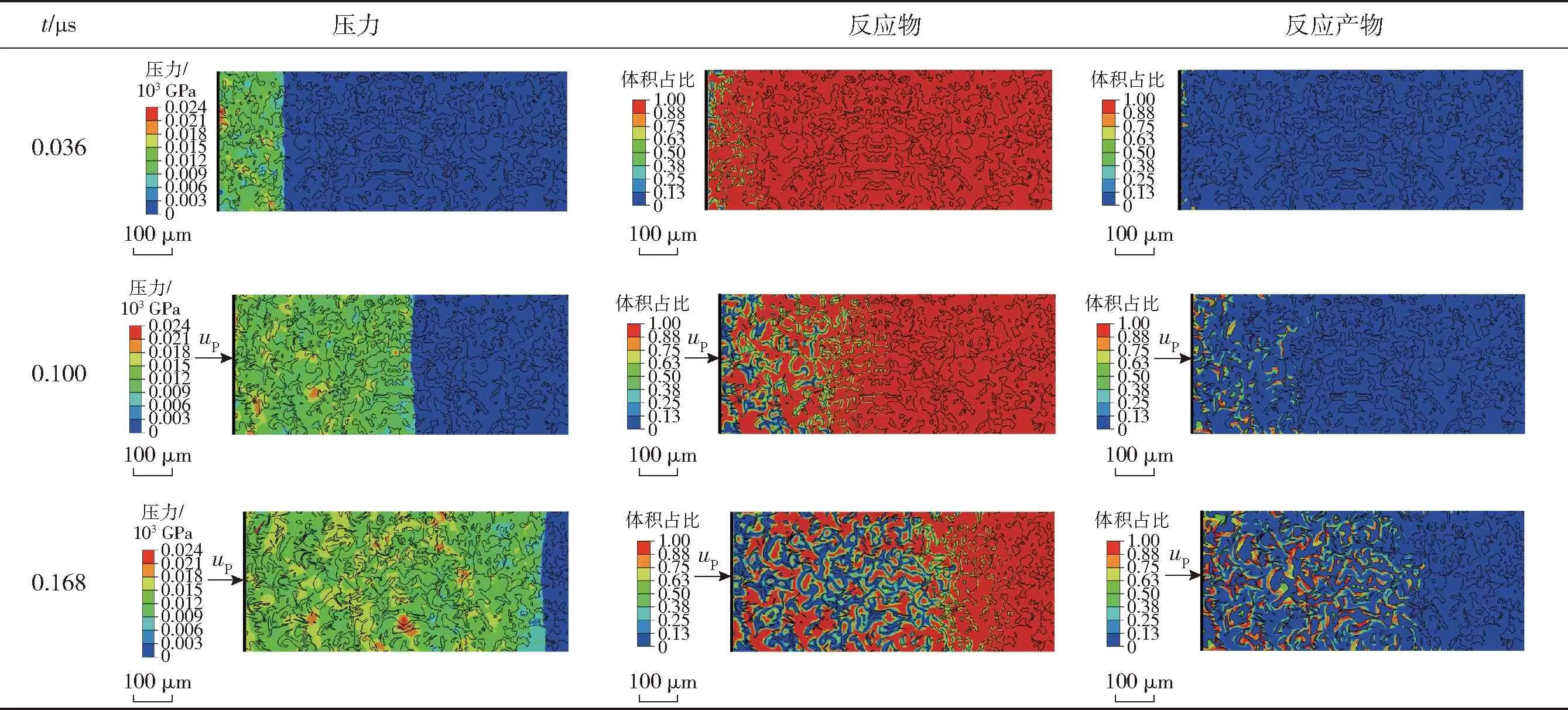
从图6中可以看出,粒径为10 μm时,各位置反应物(Al、Ni)几乎消耗殆尽,而反应产物(NiAl)几乎充满整个原始材料为Al的颗粒中,说明该粒径的Al、Ni颗粒在该加热条件下几乎发生完全化学反应。随着粒径的增大,界面左侧材料Ni的剩余量逐渐增加,而界面右侧Ni的扩散范围保持在18 μm左右。在该扩散范围(0 μm 基于前述冲击反应细观模拟方法,以Abaqus软件的VUMAT接口为平台,对Al/Ni粉末复合材料中冲击反应行为进行计算。为了分析冲击反应演化过程,提取冲击压缩速度为500 m/s(即up=500 m/s)时的冲击压力分布、反应物(Al、Ni)和反应产物(NiAl)的体积分数计算结果,如表2所示。从表2中可以看出,在冲击压缩条件下,Al、Ni颗粒发生了剧烈的变形,同时伴随着Al/Ni粉末复合材料的体积压缩。Al/Ni粉末复合材料内产生的压力均远大于材料的初始压力,并形成了明显的冲击波间断面(波阵面)。材料内部压力分布不均匀,这是由Al、Ni两种材料的波阻抗不匹配以及材料颗粒分布的不均匀性造成的,其局部压力最高可达24 GPa。当t=0.168 μs时,冲击波传播至细观结构最右端。 表2 Al/Ni粉末复合材料在500 m/s冲击压缩速度下的冲击波传播及反应物和反应产物含量演化过程 初始时刻,各位置反应物(Al、Ni)的体积分数均为1。其中,对于初始材料为Ni的细观颗粒,图中所示反应物体积分数为当前时刻材料Ni的质量与初始质量之比。由于两种材料细观颗粒间存在浓度梯度关系,在整个冲击过程中的材料Ni浓度将逐渐降低。而对于初始材料为Al的细观颗粒,可以发现其细观层中Al的体积分数也逐渐降低,说明随着材料Ni向其中扩散,Al与Ni之间发生了化学反应。另一方面,随着冲击波从左向右传播,反应产物(NiAl)的含量逐渐增加。由于本模型中只考虑Ni向Al中的扩散情况,因此反应产物仅存在于原始材料为Al的细观颗粒中。t从0.100 μs至0.168 μs的反应产物分布情况可以看出,反应产物最初产生于Al-Ni界面处,然后垂直于界面向外生长,最终在Al细观颗粒中融合。 综合以上分析可知,在冲击压缩过程中,Al/Ni粉末复合材料细观颗粒中的各组分成分及体积分数均发生了改变,说明同时发生了物质扩散和化学反应两个过程。当冲击波传播到Al-Ni材料界面时,相互接触的Al、Ni材料开始发生化学反应。同时,材料Ni从Ni颗粒向相邻Al颗粒中扩散,从而使Al、Ni材料在非界面处进一步接触,维持反应的继续发生。 此外,对比t=0.036 μs时反应物的消耗情况和反应产物的生成情况可以发现,在冲击压缩初期,冲击波波阵面后的大部分Ni的含量均有所降低,但仅在靠近加载端产生了极少的反应产物。随着冲击波的继续传播,反应物消耗的范围始终大于反应产物的分布范围,表明该冲击压缩条件(up=500 m/s)下,物质扩散速度大于化学反应速度。 图7为Al/Ni粉末复合材料在500 m/s冲击压缩速度下的温度响应结果。从图7中可以看出,强烈的冲击压缩引起了材料内温度的剧烈升高,由此触发物质扩散和化学反应两个过程。通过对比可以发现,图7所示材料内的温度分布不均匀性较压力分布结果(见图7)更为显著。在t=0.036 μs时,靠近加载端的Al/Ni粉末复合材料中存在极少的局部高温点(红色区域,接近于2 200 K),而大部分区域中温度小于1 000 K。随着冲击压缩时间的增加,局部高温区域逐渐扩大,且主要分布在Al-Ni界面处。通过与表2比较可以发现,局部高温点与反应产物的分布情况和演化规律基本相同。 图7 Al/Ni粉末复合材料在500 m/s冲击压缩速度下的温度响应结果Fig.7 Temperature response of the Al/Ni powder compaction at 500 m/s 基于2.3节冲击反应计算模型可知,Al/Ni粉末复合材料中的温度一方面由冲击压缩的塑性功贡献,一方面由冲击反应释放的能量贡献。因此,在冲击压缩过程中,Al/Ni粉末复合材料中的局部高温点对应化学反应发生的区域,局部高温区域面积越大,说明发生的化学反应程度越高。结合计算结果分析可以发现,冲击反应程度随着冲击压缩时间的延长而增大。同时, 从t=0.168 μs时表2和图7中可以看出,冲击波传播过后,波阵面后的反应产物和局部热点区域还在继续扩大,说明Al/Ni粉末复合材料反应未立即终止。研究结果表明,冲击反应具有延迟作用[13],因此该冲击反应过程将有可能在冲击波传播后延迟完成。 为了研究典型Al/Ni粉末复合材料冲击反应行为与冲击加载条件的关联机制,对400 m/s、500 m/s、800 m/s 3个典型冲击压缩速度下的反应物和反应产物分布、冲击压力和冲击温度响应结果进行分析。为了保证对比的有效性,本节所示均为冲击波传播至细观模型相同位置(冲击压缩方向中点附近)的计算结果。 3.4.1 冲击反应特性 在不同冲击压缩速度下,反应物、反应产物的体积分数及反应效率分布如表3所示。在up=400 m/s时,仅在靠近加载面处产生了极少的化学反应产物,材料内反应效率基本为0%,说明该冲击压缩速度为引发化学反应的临界条件,与相关试验测得的反应阈值(up=433 m/s)[23]吻合较好。up=500 m/s时,Al/Ni粉末复合材料内部产生了明显的反应产物,局部位置Al-Ni边界处反应效率可达到75%以上,但大部分位置反应效率为0%。随着up继续升高至800 m/s,反应产物的分布范围进一步增大,波阵面后几乎所有Al-Ni边界处反应效率达到75%以上。由此说明,Al/Ni粉末复合材料中冲击反应存在阈值条件,当冲击压缩速度较低时,无化学反应发生。随着up的增大,材料内由冲击产生的温度升高,物质扩散和化学反应速率加快,从而在冲击波传播至相同位置时产生更多的化学反应产物,反应效率得到提升。由细观模拟得到的释能规律与表1中的试验结果[23]一致,说明本文建立的冲击反应细观模型能对Al/Ni粉末复合材料的冲击释能行为进行较好地描述。 表3 Al/Ni粉末复合材料在不同冲击压缩速度下反应情况 3.4.2 冲击响应特性 Al/Ni粉末复合材料在不同冲击压缩速度下的冲击响应结果如图8所示。从计算结果可以看出,Al/Ni粉末复合材料中产生的冲击压力和冲击温度均随着冲击压缩速度的加快而升高,且细观颗粒的变形也更加剧烈。在up=400 m/s的冲击条件下,由于仅有靠近加载面的极少部分材料发生了化学反应,相应区域内温度达到了1 788 K,大部分区域温度不超过600 K。随着冲击压缩速度的上升,颗粒压缩和变形程度加大而引起冲击温度升高,最终导致局部高温区分布面积显著增大。由此说明,冲击压缩速度越高,Al、Ni间扩散反应范围越大。 图8 Al/Ni粉末复合材料在不同冲击压缩速度下的压力和温度响应结果Fig.8 Shock pressure and temperature response of the Al/Ni powder compaction at different velocities 由(17)式和(18)式可知,冲击反应将引起材料比内能和温度的增加。为了研究冲击反应对Al/Ni类粉末复合材料中冲击压缩特性的影响机制,将典型冲击加载条件下不考虑化学反应和考虑冲击反应的冲击压缩特性计算结果进行对比,如图9所示。在up=500 m/s的冲击压缩作用下,由压缩功引起的Al/Ni粉末复合材料细观结构内产生的压力最大值为 19 GPa。 基于前述分析,该冲击条件下的材料内部将发生化学反应,且考虑化学反应的峰值压力(21 GPa)高于不考虑化学反应的情况。另一方面,由压缩功引起的Al/Ni粉末复合材料中冲击温度的最大值为784 K。 当冲击反应发生后,化学反应释放的化学能将对材料内温度有所贡献,使温度峰值提高了1 217 K。 图9 Al/Ni粉末复合材料中是否考虑化学反应的冲击压力和温度计算结果对比Fig.9 Comparison of shock pressure and temperature response of the Al/Ni powder compaction with shock reaction considered/not considered 图10 Al/Ni粉末复合材料中us-up关系及冲击波速度提升率与化学反应的关系Fig.10 Calculated us-up relationship and corresponding increase rate of shock velocity in the Al/Ni powder compaction 为了进一步分析冲击反应对冲击波参数的影响规律,通过建立的Al/Ni粉末复合材料冲击反应细观模型开展300~900 m/s冲击压缩条件下冲击反应行为计算。分别提取典型时刻的冲击波波阵面传播位置,从而计算Al/Ni粉末复合材料中的冲击波速度。将考虑化学反应的Al/Ni粉末复合材料us-up曲线与不考虑化学反应的计算结果进行对比,如图10(a)所示。从图10(a)中可以看出,在up小于400 m/s时,二者吻合较好。当up达到400 m/s后,考虑化学反应计算的us-up曲线偏离于不考虑化学反应的计算结果。同时,粒子速度越高,二者us-up曲线偏离程度越大,最终趋近于平行。 将考虑化学反应后的冲击波速度相对于不考虑化学反应情况的提升率进行计算,得到其与冲击压缩速度up的关系,如图10(b)所示。由图10(b)可以看出,冲击波在本文细观模型传播的过程中,随着up从400 m/s增长到700 m/s,波速迅速提升,而在up超过700 m/s后逐渐趋于稳定。通过对不同冲击压缩速度下材料的比化学能进行分析可以发现,在400~700 m/s冲击压缩速度内材料释放的化学能与冲击波速度提升率变化趋势相似,由此说明冲击波传播速度的提升与化学反应相关。 值得注意的是,由于冲击反应程度与时间相关,因此冲击波反应对冲击波的强化作用也应与时间相关。细观尺度上冲击波的传播时间小于宏观尺度,因此此处计算得到的冲击波速度小于实际值。以上分析结果表明,化学反应的发生导致Al/Ni粉末复合材料细观结构中冲击压力和冲击温度均显著提高。在冲击压缩过程中,冲击压力和温度的提高又将继续对后续化学反应的发生和发展起到促进作用。 以Al/Ni粉末复合材料的冲击响应及冲击反应行为为研究对象,基于Mie-Grüneisen状态方程和反应扩散理论模型建立了该类材料的冲击反应细观模型,从时间尺度(冲击波的传播过程及各组分体积分数的演化规律)和空间尺度(冲击压力分布、热点及反应点的分布)分析了冲击反应细观机制。得出以下主要结论: 1) Al/Ni粉末复合材料在冲击压缩速度(即粒子速度)为400 m/s时仅发生了微弱的化学反应,说明up=400接近于冲击反应阈值。随着冲击压缩速度的增大,化学反应加剧。该规律与相关试验结果[23]吻合较好,说明利用本文建立的冲击反应细观模型能对Al/Ni粉末复合材料的冲击压缩和冲击反应行为进行较好地描述。 2)基于考虑物质输运过程的冲击反应细观模型计算结果,化学反应最初发生于Al-Ni界面处,然后垂直于界面“发展”。冲击压缩速度越高,反应扩散范围越大。 3) 冲击反应将引起材料内能、温度和压力的升高。同时,随着冲击压缩速度的增大,us-up曲线偏离于不考虑化学反应的计算结果,说明化学反应对冲击波的传播起到强化作用。3.2 Al/Ni粉末复合材料冲击反应演化过程
3.3 Al/Ni粉末复合材料冲击温度响应特性

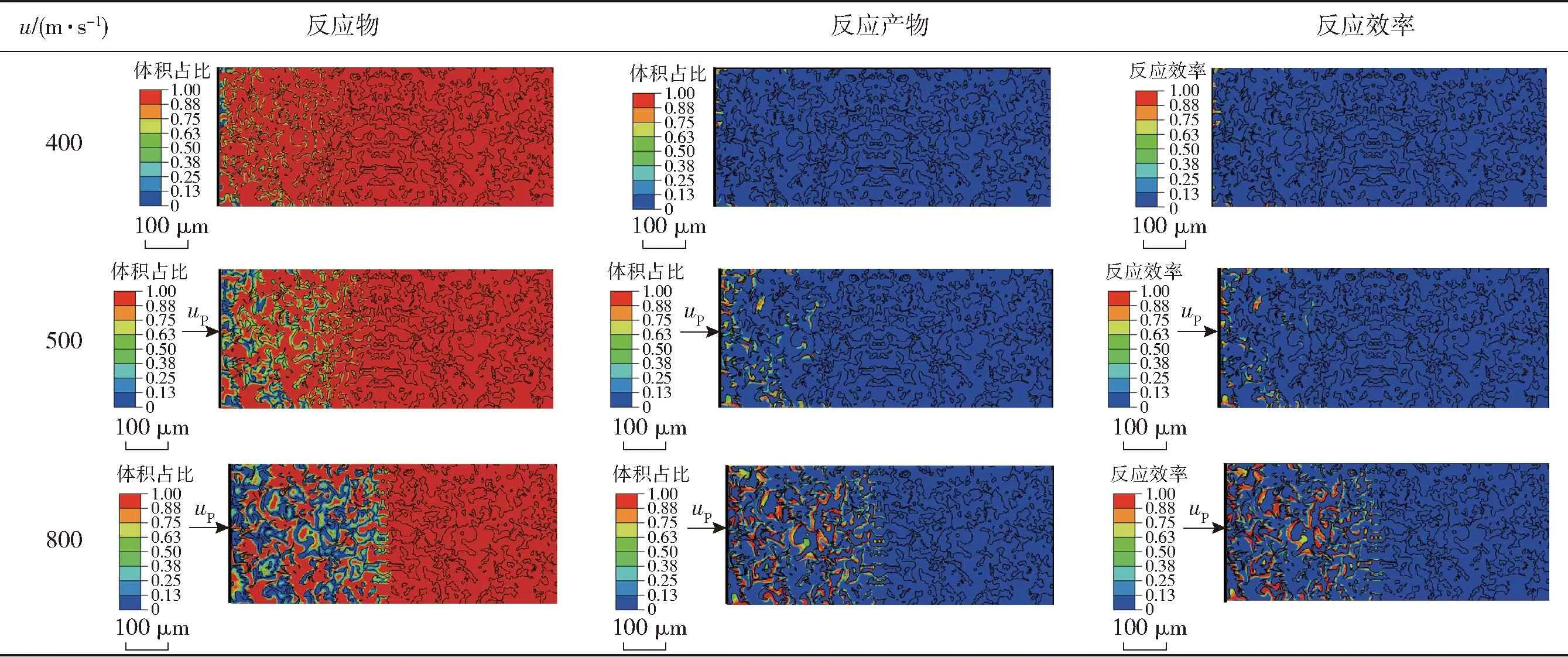
3.4 不同冲击加载条件下Al/Ni粉末复合材料冲击反应行为

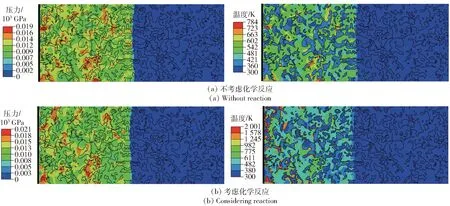
3.5 冲击反应对冲击响应特性的影响机制
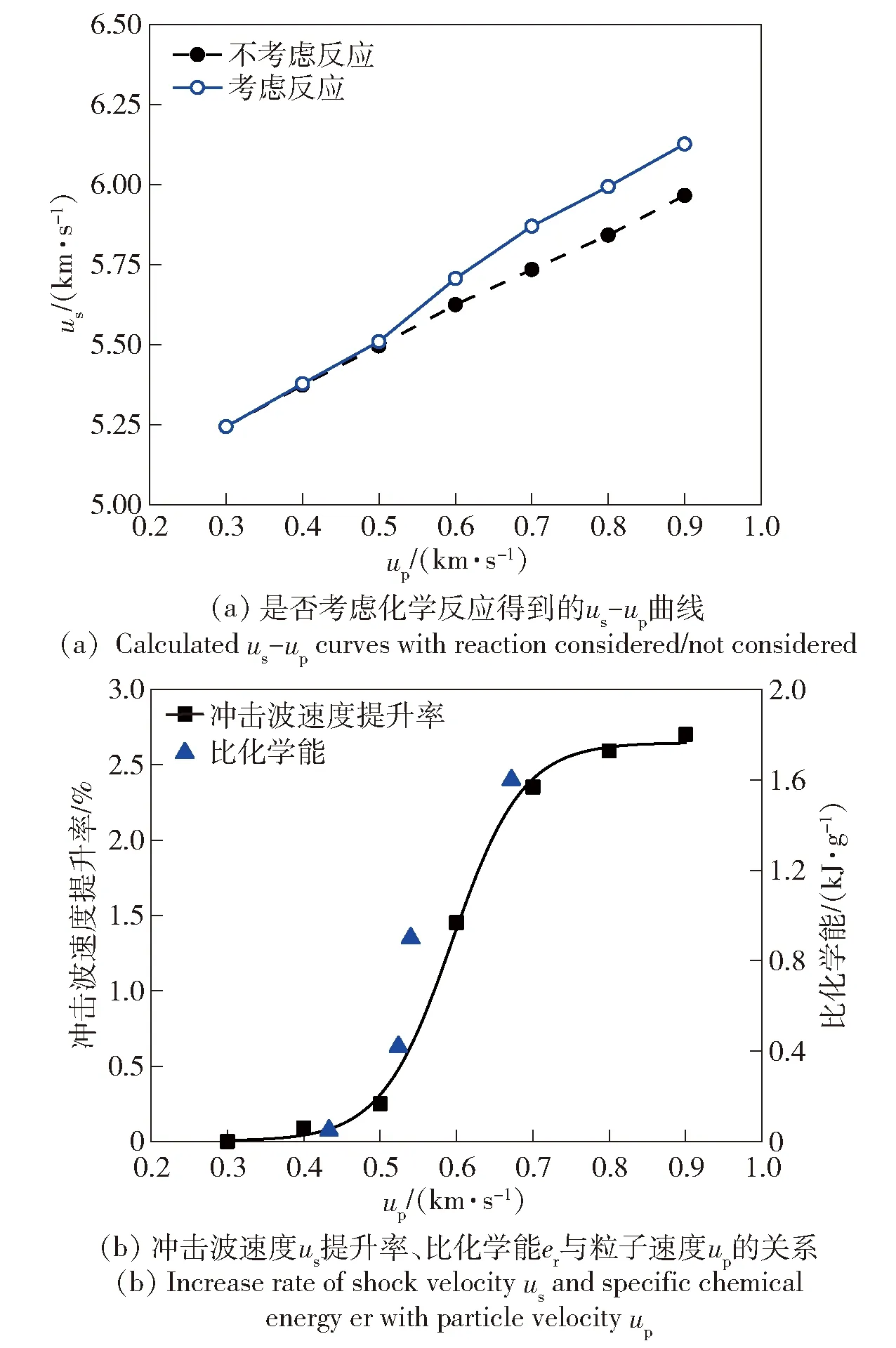
5 结论
