重载车辆进气中冷管振动特性及设计改进
2022-08-27刘宇航刘鑫张生李洪彪
刘宇航, 刘鑫, 张生, 李洪彪
(1.北京航天发射技术研究所, 北京 100076; 2.河北工业大学 化工学院, 天津 300401)
0 引言
某重载车辆在使用过程中常出现左侧进气中冷钢管损坏,造成车辆出现故障,但是右侧钢管却完好。对于重载车辆而言,由于使用工况十分复杂,零部件的失效模式也多种多样。通过观察断口微观形貌判断失效模式应为疲劳失效,由于管路并不承受强烈的高低温周期载荷,因此可排除热疲劳可能性,需对其振动特性进行研究。
频响计算是常用的计算结构在振动激励下响应的方法之一,其计算方法主要有直接法和模态法。直接法容易使用,可直接求解出位移和应力,但是计算时间长,占用资源多。模态法计算速度快,但是只适用不存在阻尼或只有模态阻尼的结构。本文采用模态法进行计算。
本文首先对某重载车辆的进气系统管路在不同工况下的振动加速度进行了测量,发现管路存在共振现象。利用频响计算发现了造成裂纹的主要振动频率。通过对比左右两侧进气中冷管结构并对设计参数进行研究,对左侧管路进行了设计改进。改进后的结构不再出现共振现象并有效改善了管路振动情况。
1 失效原因分析
进气系统的三维示意图如图1所示。发动机增压后高温高压的气体由进气弯管经右侧中冷进气钢管进入中冷器。在中冷器中,高温气体被冷却,再流经左侧中冷进气钢管进入发动机进气横通管。在此过程中新鲜充量进入发动机缸内参与燃烧并使发动机对外做功。
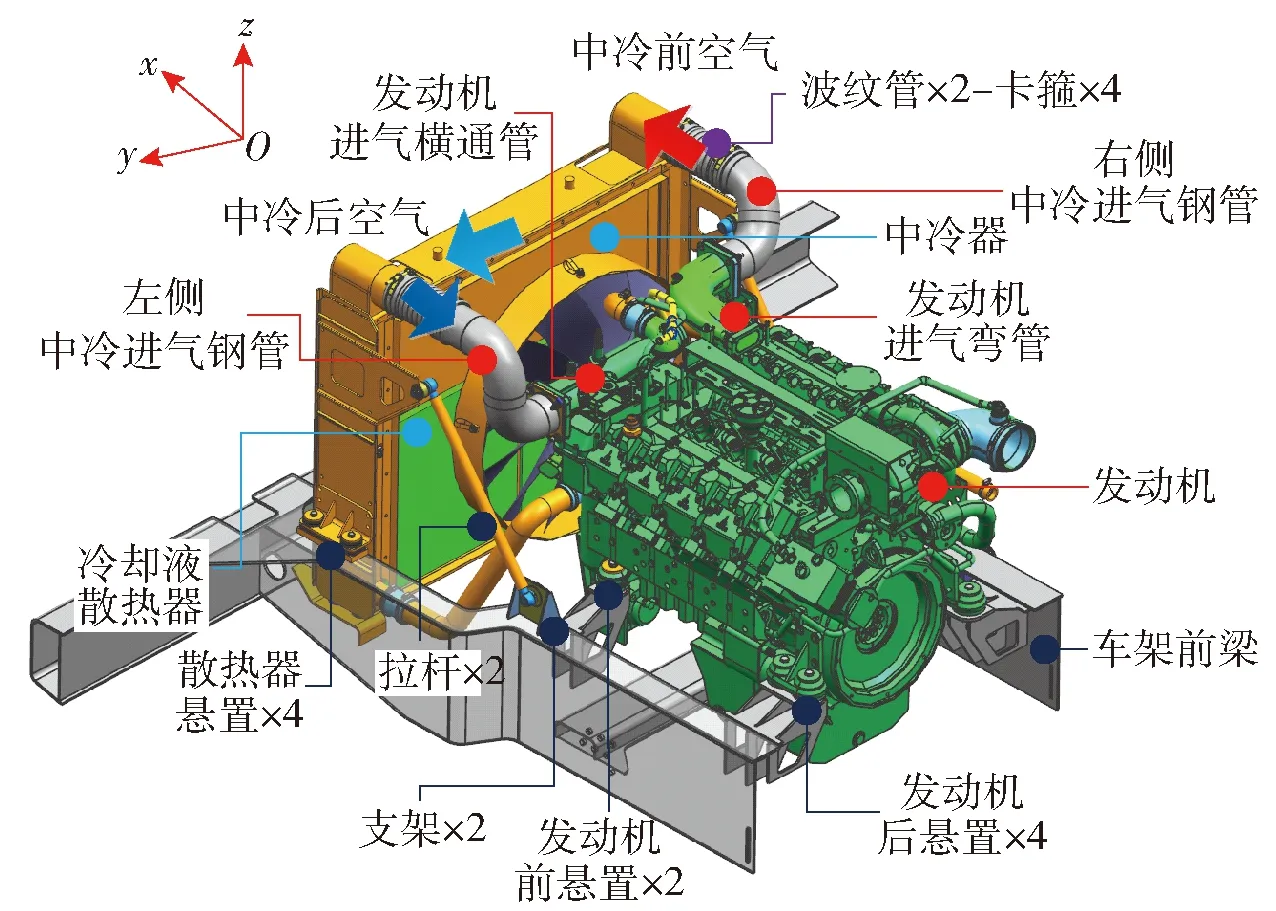
图1 进气系统示意图Fig.1 Schematic diagram of the intake system
中冷器与发动机冷却液散热器共同组成散热器总成为发动机提供冷却。散热器总成通过左右共4块悬置固定在车架前梁上平面,左右两个拉杆将散热器总成与支架连接,拉杆两端为球铰,发动机通过固定在车架前梁上的前后4个支架共6个悬置块固定。中冷器与发动机通过波纹管相连,波纹管通过卡箍分别固定在其两端。
左右侧进气中冷钢管的材质皆为不锈钢(1Cr18Ni9Ti),材料属性如表1所示。在使用过程中,左侧进气中冷钢管裂纹常出现在钢管与其相连的法兰盘根部。失效钢管如图2所示,其裂纹形貌如图3所示。图3中的视图方向与图2同为俯视图。通过扫描电镜对断口部位进行微观形貌观察及能谱分析,如图4所示。由图4可以看出,断口呈现疲劳条带状形貌,据此判断失效模式应为疲劳失效。

表1 材料属性

图2 进气中冷管裂纹位置Fig.2 Cracks on the intake-cooling pipes

图3 裂纹形貌Fig.3 Crack morphology

图4 裂纹断面微观形貌Fig.4 Cross-section microcosmic morphology of the crack
2 试验建立
2.1 测点位置及信号采集
针对进气系统进行振动测试,其测点位置及数据处理流程如图5所示,布置6个测点位置。每个测点位置上布置一个加速度传感器,以测量每个测点的振动加速度信号。
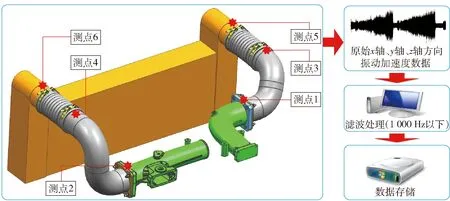
图5 振动测点位置及数据处理流程Fig.5 Measuring points and data processing flow
测点1、测点2分别布置在发动机进气弯管和进气横通管与左右进气中冷钢管连接的法兰盘顶端。测点3、测点4分别布置在进气中冷钢管与波纹管连接处顶端。测点5、测点6分别布置在中冷器左右铸管与波纹管连接处顶端。
每个测点位置的加速度传感器可采集轴、轴、轴3个方向的振动加速度信号。原始信号采集系统的采集频率为2 000 Hz,经过滤波后的处理信号为1 000 Hz。
2.2 试验工况定义
对于本文所研究的重载车辆,较为常用的工况为运输工况及原地取力工况。因此,定义试验工况如表2所示。针对每一个试验工况,待试验工况稳定后30 s开始收集数据,收集时间为10 s。每个工况进行两次试验,取两次试验的平均值作为最终试验测量值。
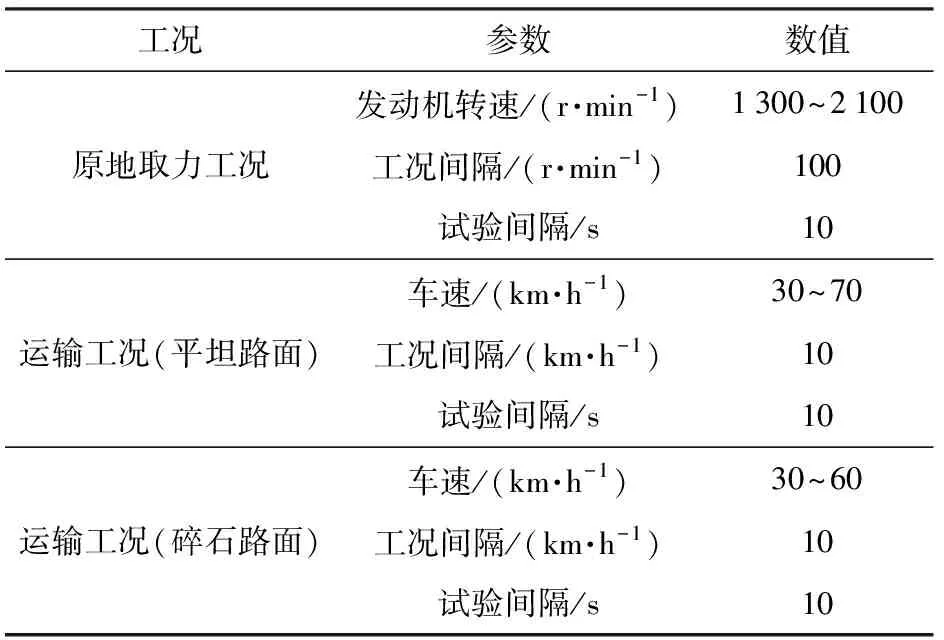
表2 试验工况定义
3 加速度数据分析
原地取力工况下,不同测点所测得的振动加速度值随发动机转速的关系如图6所示。由图6中可以看出,随着发动机转速的升高,测点1、2、5、6的振动加速度值呈现逐渐升高的趋势。这主要是随着发动机转速的提高,发动机本体的不平衡力矩会使发动机的振动烈度增加。发动机的振动通过车架传递至散热器会引起散热器的振动。测点4的振动加速度值在发动机转速为1 700 r/min时有明显的升高,表明左侧进气中冷管在该发动机转速工况下工作异常。
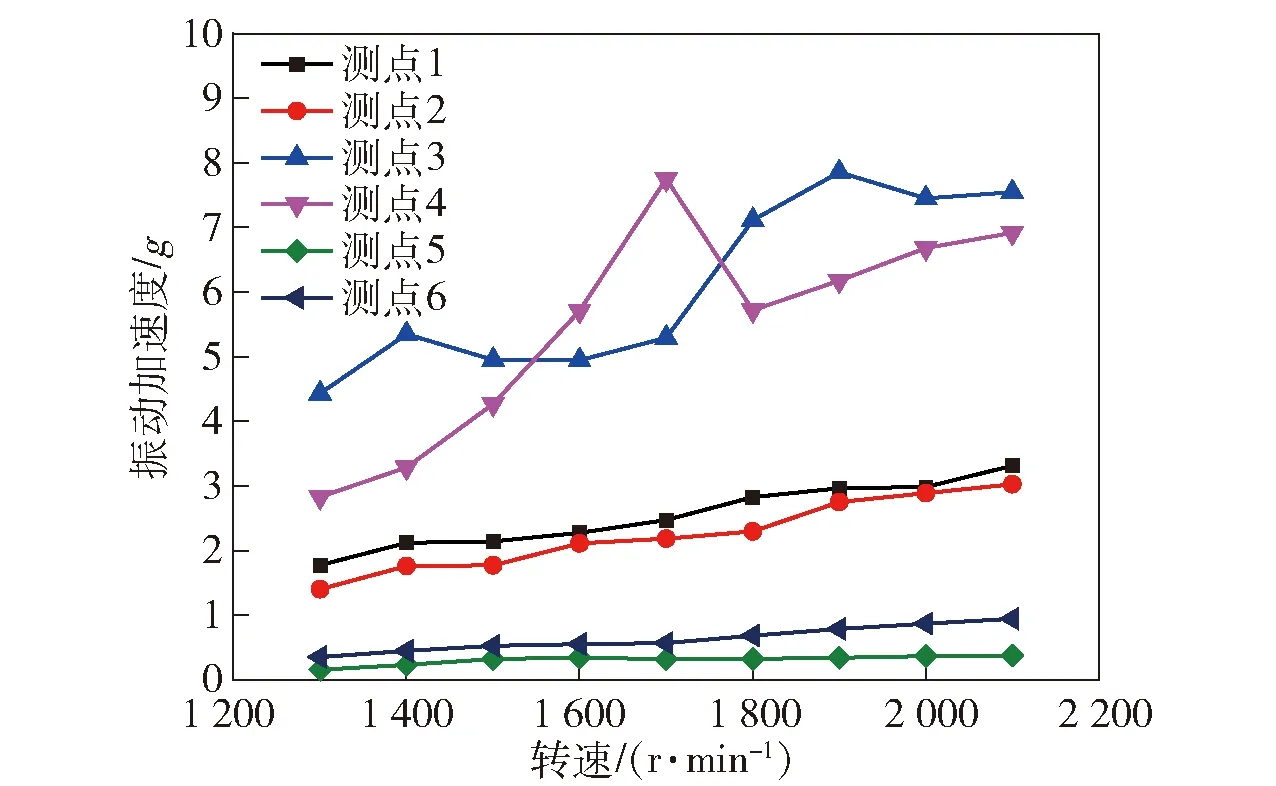
图6 原地取力工况下不同测点加速度测量值Fig.6 Acceleration values under different in situ conditions
测点3在发动机转速为1 900 r/min时与测点4在1 700 r/min时有相近的加速度值。对比测点1~测点4不同方向的振动加速度值如图7所示。由图7 可以看出,由于测点3、4的振动主要由与发动机相连的进气管路引起,测点1、3和测点2、4在不同方向上的振动加速度变化趋势是相同的。通过比较振动加速度大小可以发现,测点3、4沿轴方向的振动加速度数值较为近似,但是测点3沿轴方向的振动较为剧烈,测点4沿轴方向的振动较为剧烈。

图7 测点1~测点4不同方向振动加速度值Fig.7 Acceleration values at measured points 1~4
平坦路面及碎石路面不同车速各测点的振动加速度值及该工况下所对应的挡位如图8、图9所示。由图8、图9可以看出,测点5、测点6振动加速度值变化并不明显,表明散热器的振动对车速和路面的变化并不敏感。测点1、测点2的振动加速度值随着车速的升高,呈现增加的趋势,但是分别会在 60 km/h 和50 km/h时出现一定波动。这主要是由于在行驶工况下,一方面,挡位的调节会影响发动机转速,发动机转速的变化会影响测点振动加速度值;另一方面,路面所传递的振动激励同样会影响测点1、测点2的振动测量值。测点3、测点4在平坦路面工况下,振动加速度值会随着车速的增加呈现增加的趋势;在碎石路面工况下,呈现上凹的曲线形式。

图8 平坦路面工况下不同测点加速度测量值Fig.8 Acceleration values under different flat road conditions
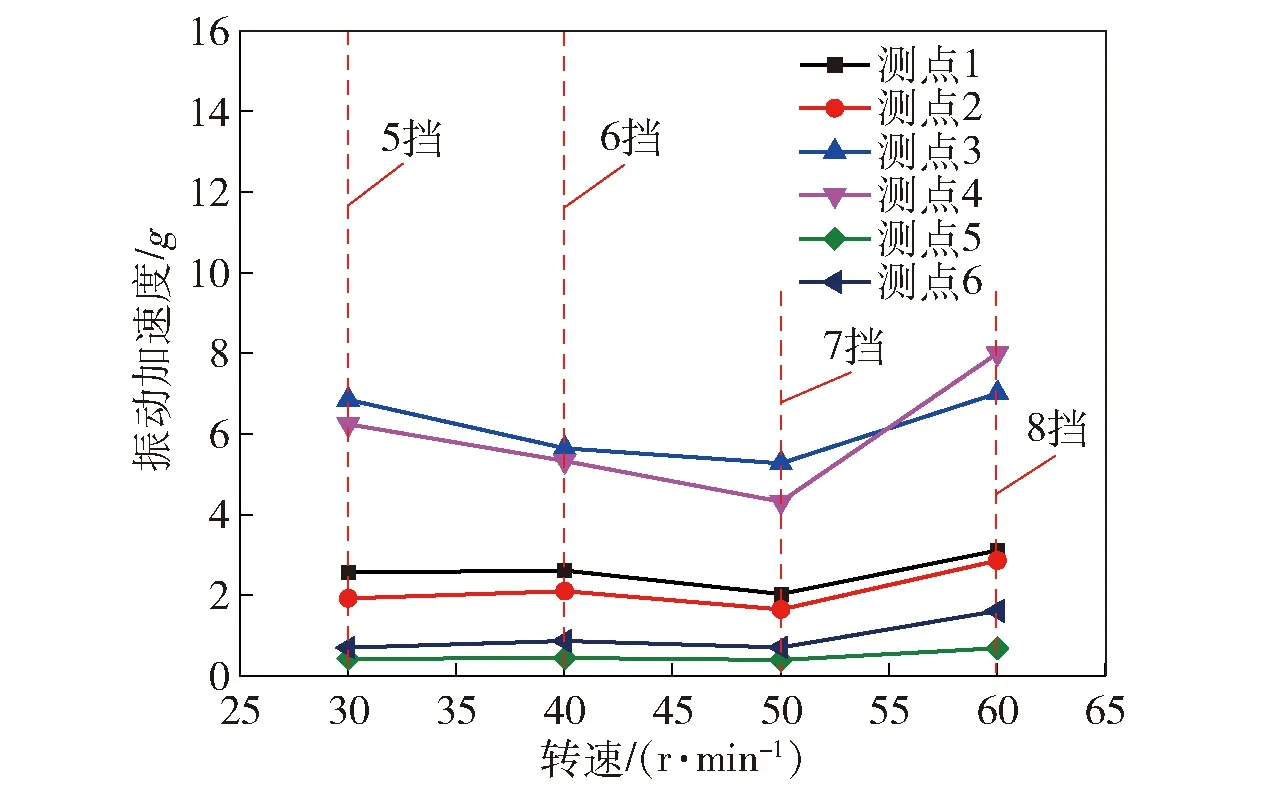
图9 碎石路面工况下不同测点加速度测量值Fig.9 Acceleration values under different gravel road conditions
综合图6、图8、图9可看出,左右侧中冷进气钢管的振动加速度值最大,发动机进气弯管和进气横通管其次,散热器铸管的振动加速度值最小。无论在哪种工况下,测点6的振动加速度都大于测点5,表明散热器左侧比右侧振动更大。无论在哪种工况下,测点1的振动加速度值都大于测点2,表明发动机右侧比左侧振动更大。
左右侧进气中冷钢管一端与波纹管相连,另一端分别通过螺栓与发动机进气横通管和发动机进气弯管相连。由于波纹管为软连接,左右侧进气中冷管的振动主要由发动机的激振引起。因此,考虑对测点1、2的振动加速度信号进行频域分析,考察其主频成分。
4 频域分析
对发动机转速1 700 r/min,整车原地取力工况下采集的测点1、测点2的振动加速度信号进行傅里叶变换可以将时域信号转换为频域信号。由于本文所研究柴油机的额定转速并不高且路面对整车的激励频率一般不超过100 Hz,而且高频成分一般对车辆部件的影响较小,因此本文关注的频率范围为0~200 Hz。测点1、测点2的频域信号如图10(a)所示,图中曲线的峰值即表示了组成振动信号的主频成分。读取图10(a)中0~200 Hz范围内的峰值可以得到图10(b)。由图10可知,测点2相比测点1主频成分多出了100 Hz和112 Hz,其余部分测点1、测点2主频成分基本保持一致。

图10 测点1、测点2频域信号及主频成分Fig.10 Frequency domain signals and main dominant frequencies of Point 1 and Point 2
综上可知,测点1和测点2的主频成分相差不大,造成中冷管失效的原因应该是左右侧中冷管的不同结构在振动激励下的响应不同。因此,考虑对左侧进气中冷管进行频响计算。
5 频响计算
5.1 有限元模型
对左侧进气中冷管建立有限元模型,如图11所示。图11中坐标与图1中所示坐标相同。模型由管壁和法兰盘两部分组成。两部分都使用shell单元,左右两侧中冷管的法兰盘厚度皆为8 mm,管壁厚度皆为1.5 mm。由于中冷管与法兰处通过焊接相连,在此处增加weld单元。将法兰盘上的节点通过rb2单元与法兰盘中心连接,用以在后续计算中施加加速度载荷。
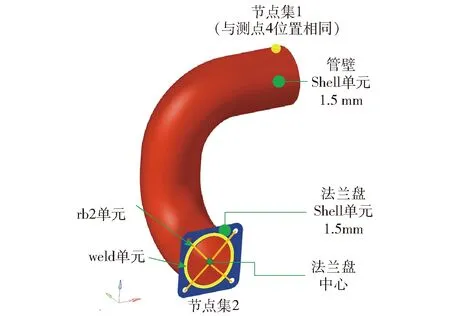
图11 有限元模型Fig.11 Finite element model
在有限元模型中建立两个节点集。节点集1如图11中黄点所示,包含图5中与测点4位置相同的节点。节点集2如图11中黄色曲线所示,包含钢管与法兰盘交界处的所有节点。节点集1用于提取振动加速度结果,来验证模型准确性。节点集2用于提取最大节点应力。
5.2 模型验证
图12中黑色曲线为当发动机转速1 700 r/min,整车原地取力工况下测点2的部分时域信号。将所示的时域加速度载荷施加在图11所示有限元模型的法兰盘中心节点进行计算,并提取节点集1的振动加速度值与试验数据进行对比。

图12 不同方向试验与仿真振动加速度值比较Fig.12 Simulated and experimental vibration acceleration values for different directions
节点集1与试验所得振动加速度均方根值对比如表3所示。由表3可以看出,试验与模型仿真的误差在5%以内,验证了仿真计算的可行性。
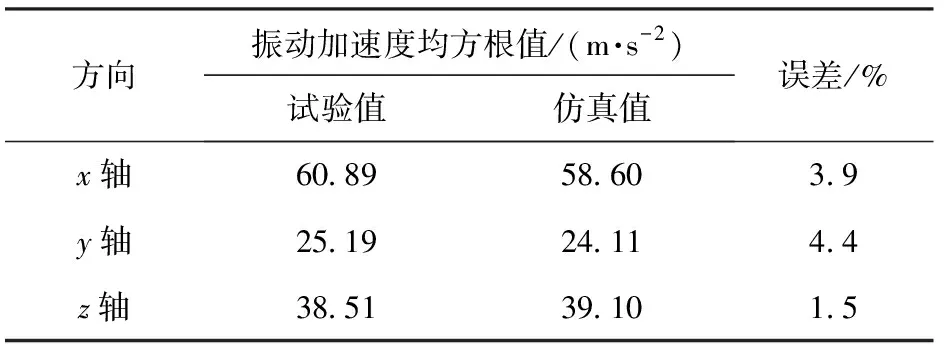
表3 试验与仿真振动加速度均方根值对比
5.3 频响计算
发动机转速1 700 r/min,整车原地工况下测点2的振动加速度均方根值如表4所示。将其作为加速度载荷边界条件施加在图11所示有限元模型的法兰盘中心节点进行频响计算,计算频率范围为1~200 Hz,计算间隔为1 Hz。得到节点集2的最大应力与频率的关系曲线,如图13所示。

图13 试验曲线与频响曲线对比Fig.13 Comparison of experimental data and frequency response simulation curve
按照同样的方法对右侧中冷管进行计算并做对比分析,右侧中冷管的加速度载荷边界条件如表4中测点1所示。
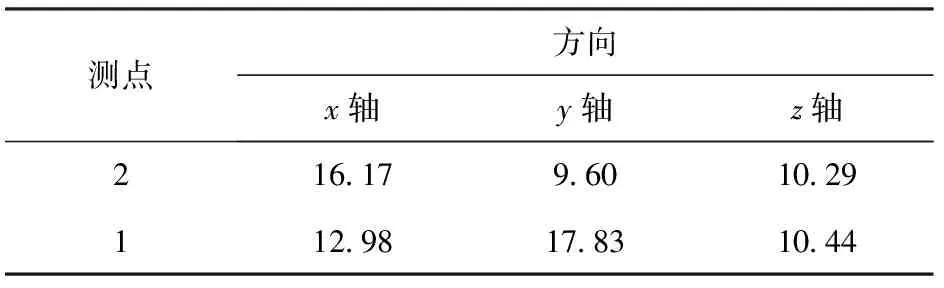
表4 测点1、测点2振动加速度均方根值
将图10中测点1、测点2的主频成分同样放在图13中可以发现,随着频率的增加,左侧中冷管根部节点应力在138 Hz出现峰值,与测点2的主频成分吻合,表明左侧中冷管在该频率下发生共振现象,所对应的应力值为74.2 MPa。当零件存在应力不均且经过一定次数的循环载荷后即可产生微裂纹进而发展成为宏观裂纹,而且裂纹也往往发生在应力较大处。右侧中冷管根部节点应力在0~200 Hz范围内并未出现峰值,表明管路并未发生共振现象。因此,左侧中冷管会发生失效现象而工况十分相似的右侧中冷管并不会发生失效。
6 设计改进
6.1 左右中冷管设计对比
由5.3节中所述,对于左右侧中冷管而言,右侧中冷管在激振加速度更大的情况下相比左侧中冷管并没有出现失效现象。左侧中冷管的失效原因主要是与138 Hz主频振动发生共振。从改进设计的角度而言,需要对比左右两侧中冷管的设计参数,如表5所示,其中Δ、Δ、Δ分别代表管路两端在轴、轴、轴方向的投影长度。
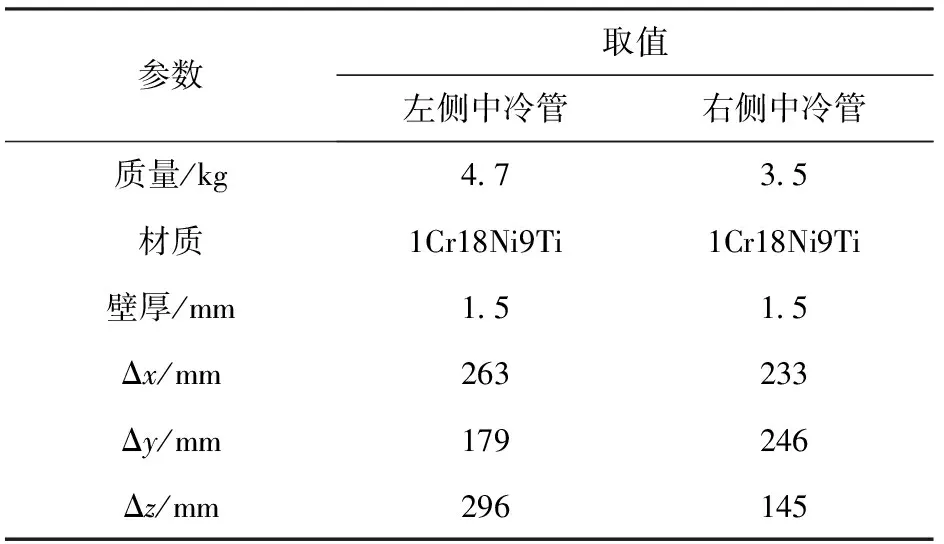
表5 左右侧中冷管设计参数对比
由表5可知:左右两侧中冷管管壁厚度和材质相同,Δ相差不大;右侧中冷管质量更小;左侧中冷管Δ更大,而右侧中冷管Δ更大;左侧中冷管相比右侧质量更重。结合图1,对于左侧中冷管而言,Δ的改变会导致中冷器管路侧向连接变得复杂,因此结构上可考虑从调整Δ、Δ来进行设计改进。质量上可考虑调整钢管壁厚来改进设计。
6.2 设计变量分析
取原左侧中冷管设计参数Δ、Δ的0.8、0.9、1.0、1.1、1.2倍进行计算,读取频响曲线的第1个应力峰值及峰值出现的频率,来研究设计参数对计算结果的影响,如图14所示。由图14可知:Δ的增加会使管路应力峰值呈现下降的趋势;Δ的增加会使管路应力峰值呈现明显升高的趋势;Δ、Δ的增加都会使应力峰值出现的频率减小;Δ的变化对应力峰值和峰值频率的影响相比Δ更加明显。因此,考虑通过减小Δ来降低应力峰值从而改善设计。

图14 Δx、Δz对计算应力峰值及峰值对应频率的影响Fig.14 Effects of Δx、Δz on peak stress and corresponding frequency
对左侧中冷管壁厚取1.5~3.5 mm,间隔为 0.5 mm 进行计算,所得结果如图15所示。由图15可知,壁厚的增加会使应力峰值呈下降趋势。应力峰值所对应的频率呈现上升的趋势。从振动的角度而言,壁厚的增加有利于降低应力峰值、避开共振频率。但是,从结构上而言,本文所研究的冷管类似悬臂机构且对于重载特种车辆,使用过程中的冲击载荷同样是十分重要的考量标准。壁厚的增加使管路质量增加,势必会加剧管路在冲击载荷中的可靠性风险。因此,不考虑从壁厚方面进行设计改进。
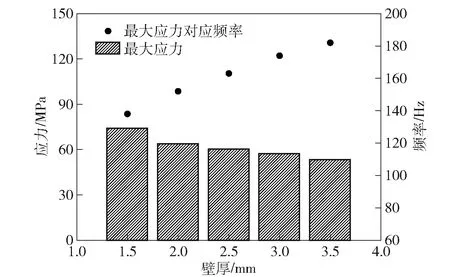
图15 壁厚对应力峰值及峰值对应频率的影响Fig.15 Effects of pipe thickness on peak stress and corresponding frequency
6.3 方案对比
如图16所示,管路需要连接的散热器端与发动机端接口位置无法改变。原方案钢管通过一段直波纹管连接散热器端接口与钢管自由端,由于需要降低Δ方向高度来改进设计,考虑采用一段弯波纹管与中冷管相连的方案。
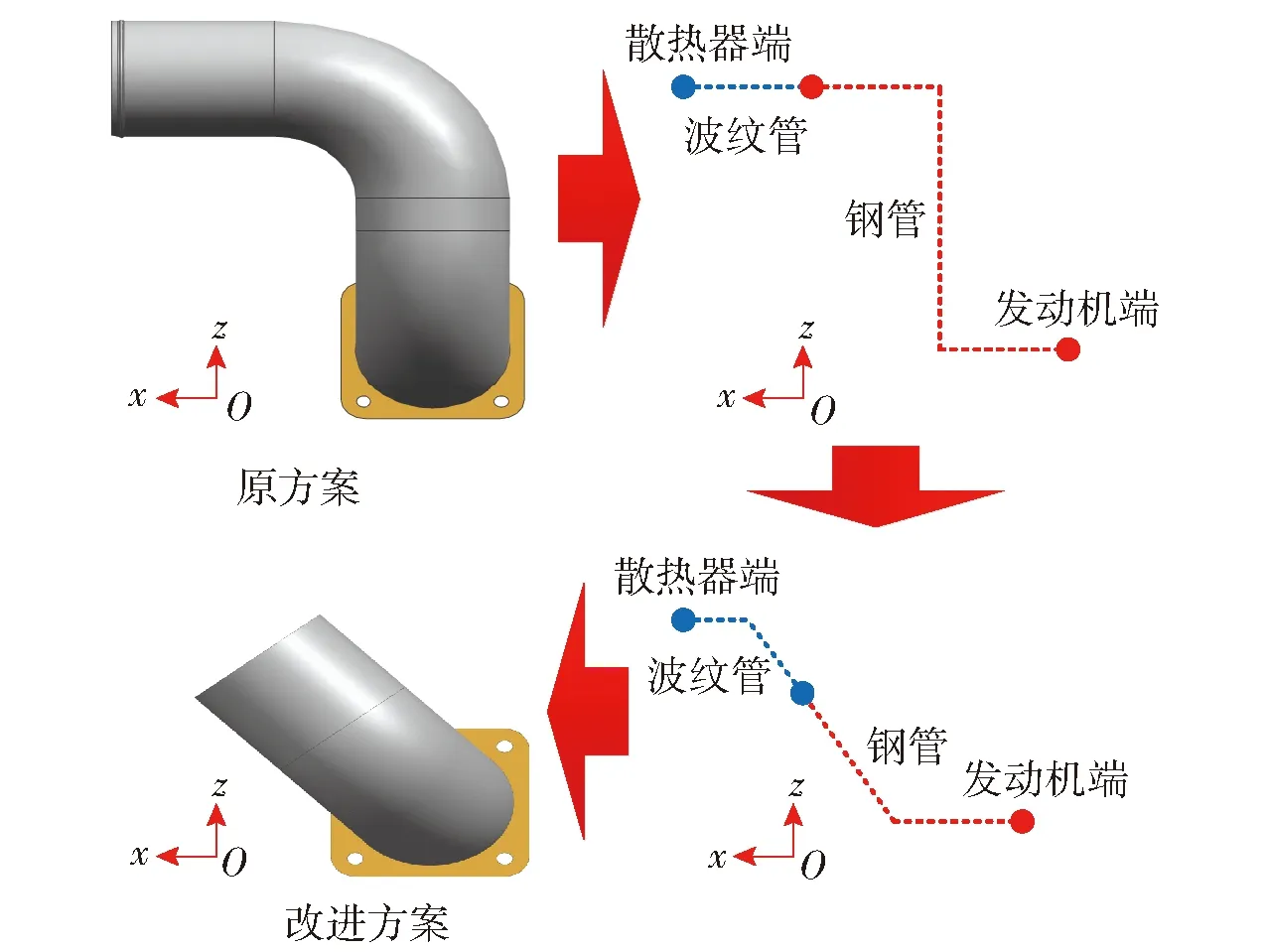
图16 左侧中冷管设计改进Fig.16 Improved design scheme for the left inter-cooling iron pipe
参照本文对原方案进行的频响计算,对改进方案施加相同的加速度边界条件进行计算,可以得到改进方案与原方案管路根部与法兰盘连接处最大应力的频响曲线如图17所示。由图17可知,改进后的设计方案在0~200 Hz内不会出现应力峰值。因此,改进方案不会在发动机1 700 r/min,车辆原地取力工况下发生共振现象。
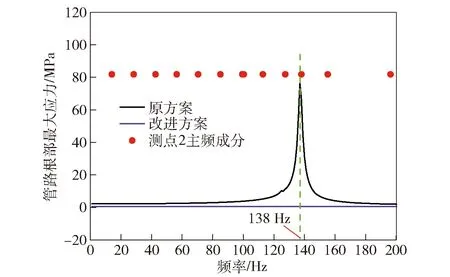
图17 原方案与改进方案频响曲线对比Fig.17 Comparison of the original and developed schemes in terms of the frequency response curve
7 疲劳预测
针对改进前和改进后的中冷管进行疲劳计算。由于中冷管在使用过程中的应力水平并不大,寿命次数较高,因此应属高周疲劳。由测点2所测的时域加速度信号所转换的功率谱密度如图18所示。循环应力由Goodman方程修正。根据nCode软件推荐方法计算材料的应力- 寿命曲线,如图19所示。通过计算所得两种方案的损伤云图如图20、图21所示。由图20可以看出,所计算处的损伤较大位置与图3所示裂纹位置基本吻合。相比较图20、图21可以看出,改进后的中冷管损伤得到了有效的降低。

图18 加速度功率谱密度图Fig.18 Power spectral density diagram of acceleration
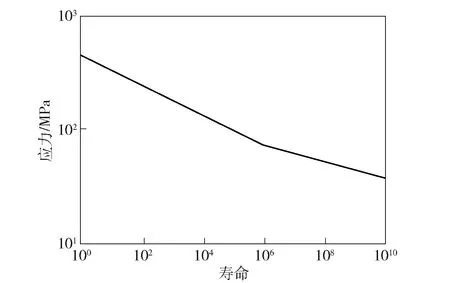
图19 中冷管材料应力- 寿命曲线Fig.19 SN curve of the material for inter-cooling pipes

图20 原方案疲劳损伤计算云图Fig.20 Fatigue damage contour nephogram of the original design scheme
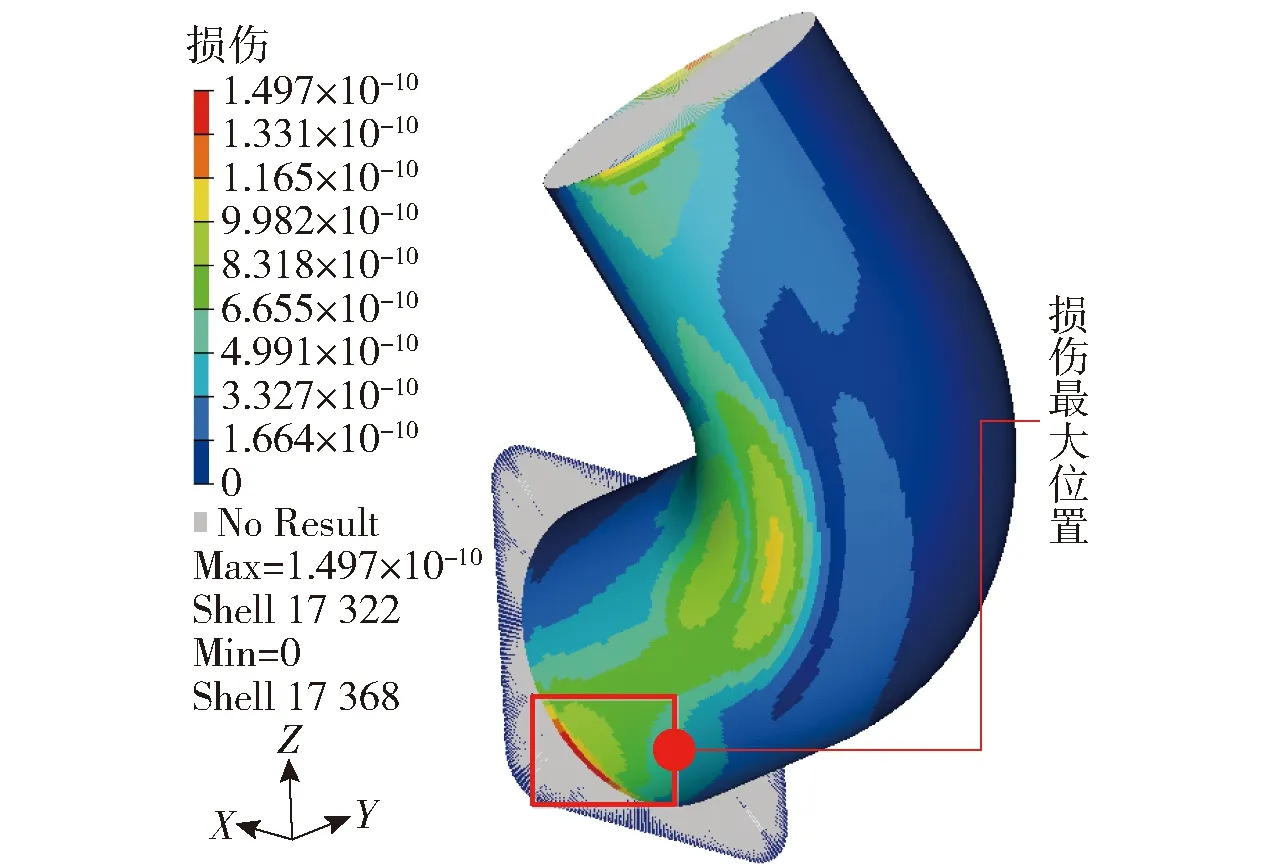
图21 改进方案疲劳损伤计算云图Fig.21 Fatigue damage contour nephogram of the optimized design scheme
8 试验验证
为验证改进方案的有效性,同时也为了避免改进方案在其他工况下出现共振现象,针对改进后的方案进行了试验验证,结果如图22所示。试验采用与表2相同工况与采样时间,读取加速度传感器1的试验数据并进行处理可得到图23~图25所示结果。由图23~图25可以发现,结构改进后的进气管在各工况下都不会出现振动加速度异常的情况。在原地取力工况及平坦路面工况下,管路的振动加速度有明显的下降,证明管路在工作状态下的振动环境得到了明显改善。对于碎石路面工况,原状态下所测得测点4的振动加速度随车速的增加呈现下凸的形状。改进结构后加速度传感器1所测得的数据随车速的增加呈现上凸的形状。虽然在车速 50 km/h 工况下,改进后的管路加速度相比原结构有所增加,但是在其余工况下振动加速度数值都有明显减小。综上,改进后的结构形式可以有效减小工作状态下的振动加速度,改善管路的工作环境,增加使用寿命。

图22 试验图片Fig.22 Experimental setup
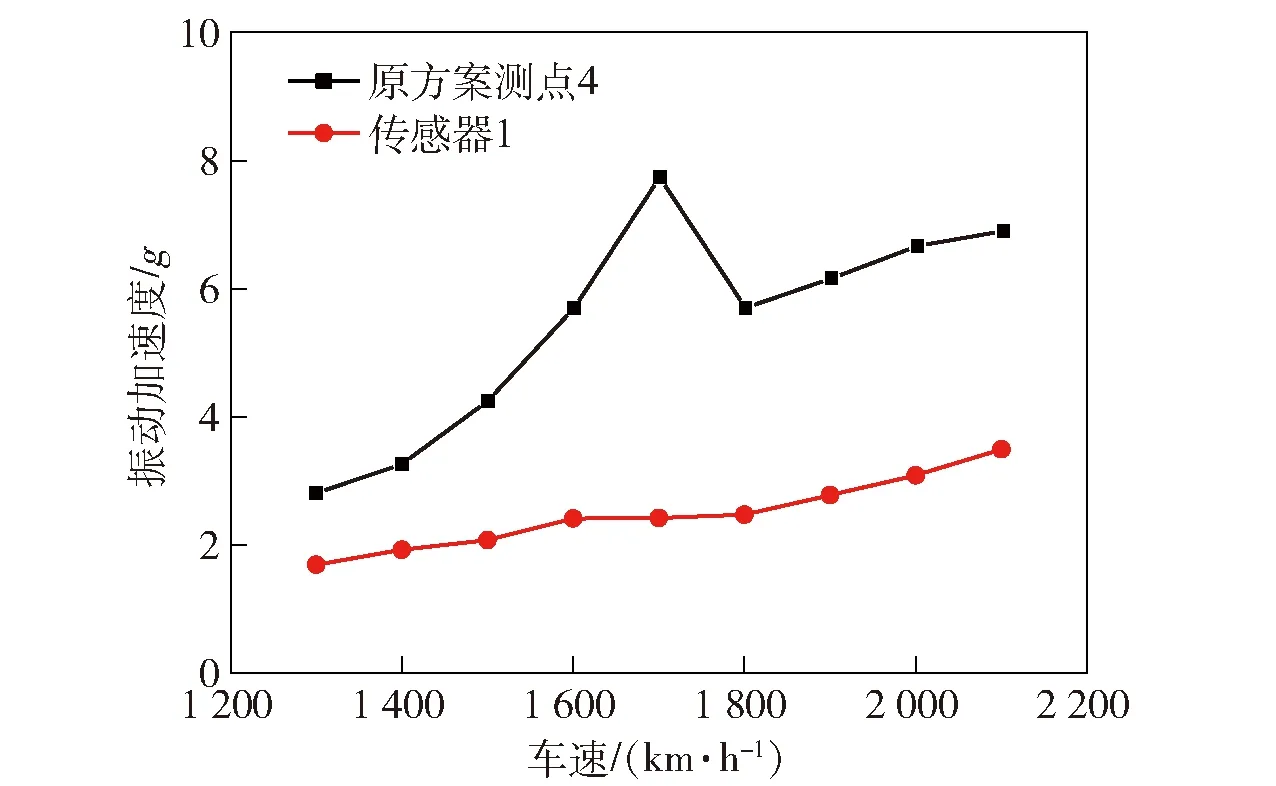
图23 原方案与改进方案原地取力工况振动加速度比较Fig.23 Comparison of the original and developed schemes in terms of vibration acceleration under in-situ condition
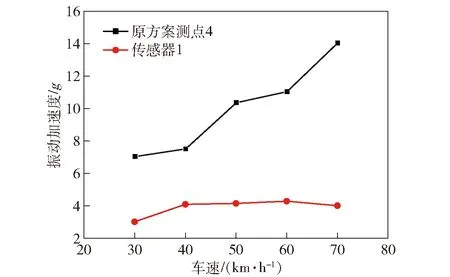
图24 原方案与改进方案平坦路面振动加速度比较Fig.24 Comparison of the original and developed schemes in terms of vibration acceleration under flat-road conditions
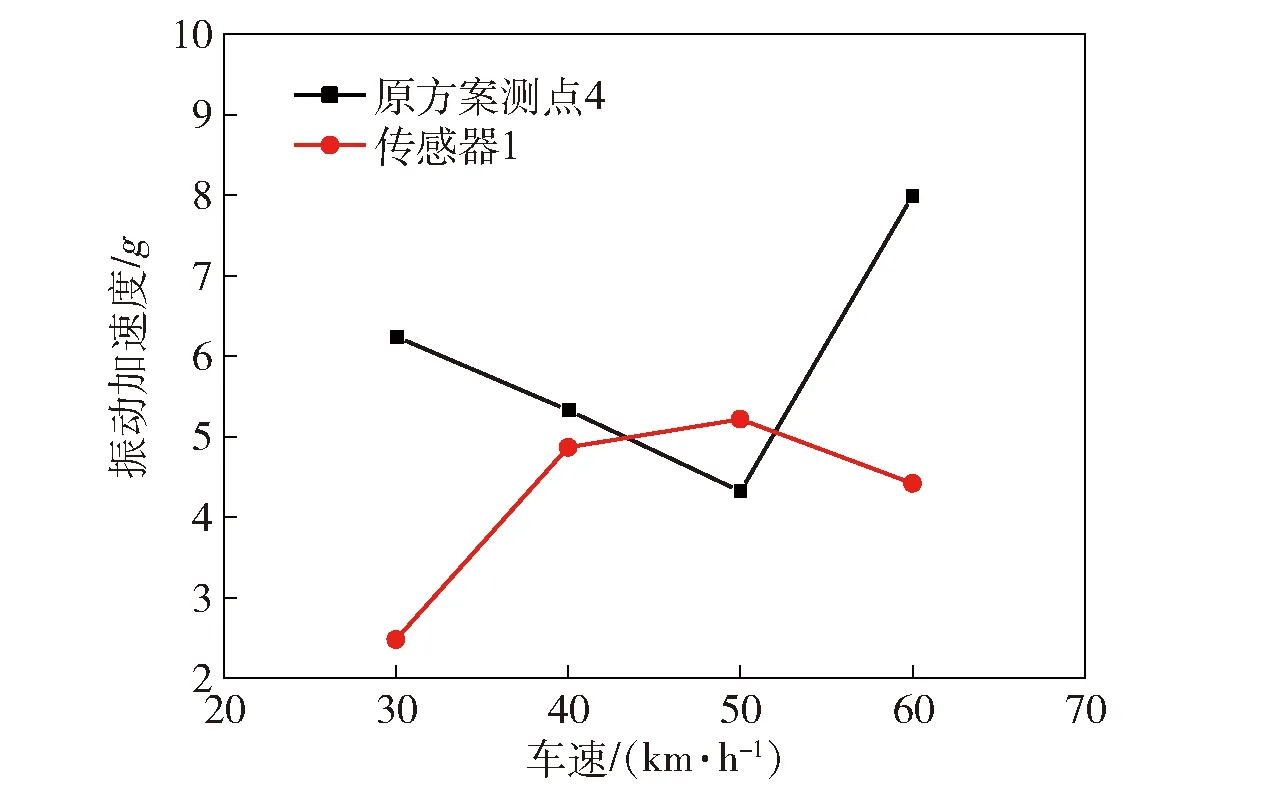
图25 原方案与改进方案碎石路面振动加速度比较Fig.25 Comparison of the original and developed schemes in terms of vibration acceleration under gravel road conditions
由于最终方案相比原方案波纹管长度增加,从可靠性角度对波纹管进行了重新设计,如图26所示。波纹管采用内外硅橡胶夹织物增强层的设计,以保证管路的拉伸强度和撕裂强度。环箍确保管路具备一定整体刚度。新方案经过实车使用,状态良好。

图26 改进方案硅胶管结构示意图Fig.26 Structural diagram of the improved silicone pipe
9 结论
本文研究了中冷钢管在使用过程中产生损坏的问题。经过试验和计算,发现中冷钢管的损坏主要是由于振动问题造成的。通过对设计参数的研究,对原设计进行了改进并取得了较好的效果。得出以下主要结论:
1)左侧中冷管的失效模式属于疲劳失效,在车辆原地取力、发动机1 700 r/min工况下会发生共振,振动加速度为59.68 m/s。
2)在原地取力、平坦路面、碎石路面工况下,右侧中冷管路所受到的激振加速度相比左侧更大。
3)左侧中冷管共振频率发生在138 Hz,此时钢管根部最大应力值为74.2 MPa。
4)对于左侧中冷管而言,随着Δ、Δ的增加,管路最大应力分别呈现减小和增大的趋势。但是应力峰值出现的频率都会随着Δ、Δ的增加呈现减小的趋势;Δ的减小更能有效降低管路应力峰值。
5)通过对左侧进气钢管进行结构改进,改进后的结构在0~200 Hz内并没有出现应力峰值,疲劳损伤有效降低。
6)通过试验对比改进前和改进后设计方案发现除碎石路工况,车辆行驶速度50 km/h时改进后中冷管振动加速度有小幅上升,其余工况都明显降低。
