混合信息熵约束下的电源车传感器优化配置方法

蒋栋年， 李炜

(1.兰州理工大学 电气工程与信息工程学院， 甘肃 兰州 730050；2.国家电网甘肃省电力科学研究院， 甘肃 兰州 730050；3.兰州理工大学 甘肃省工业过程先进控制重点实验室， 甘肃 兰州 730050)

0 引言

电源车作为一种军用移动电站，是野外条件下军队武器装备的主要电能来源，被称之为武器系统的“心脏”，一旦出现故障，整个武器系统都可能陷入瘫痪而贻误战机。为系统配置功能齐全、类型丰富的各类传感器是提高故障诊断精度、保证系统安全运行的重要手段之一。然而电源车空间有限，且部分测点传感器价格昂贵，无法有效保障传感器测量与故障一一对应。因此，对测点传感器进行优化配置是实现电源车故障检测和隔离的关键所在，也是保障电源车运行在安全可靠状态的前提。在电源车故障诊断传感器优化配置中既要满足对可能发生的故障进行全覆盖的检测，还要对配置数量和位置进行优化，满足传感器配置经济性和可现实性的协同。

近年来，很多学者就传感器的优化配置进行了深入研究。文献[6]在水质检测网络中提出了一种基于信息值的测点优化配置方法，当水质发生变化时，不同的监测点获取的信息值是不一致的，以此来作为传感器最优配置的依据。信息值是一种衡量随机信号信息量的方法，最早被决策者应用于投资是否具有经济性的评估。类似的，文献[8]利用信息值进行超声导波检测传感器的优化配置，并借助相对期望信息增益，作为确定传感器最佳数量和位置的最优性准则。文献[9]提出一种新的网络化系统信息值管理方法，以便于有效估计系统状态，从而实现了实体之间通过公共通讯网络共享数据的目的。文献[10]利用信息值研究了量值优化传感器监测方案的子模块性问题。

受信息值方法的启发，对于基于故障可诊断性评价的电源车传感器优化配置问题，本质上也是通过度量不同测量传感信息的变化来实现的。当系统发生故障时，由于故障的传播，会引起传感器的测量数据发生变化，这就会导致传感器获取的信息值发生变化，由此可以作为故障被检测的判断依据。不同的故障情况下，传感器集合获取的信息值是不一样的，将传感器网络得到的信息值期望作为标准，就可以进行不同故障之间的隔离。

然而，即使利用信息值的量化评价方法获取测点传感器的配置集合，依然存在两个问题需要解决：一是由于传感器集合内部可能存在信息冗余，不同的传感器配置集合可能拥有相同的信息值；二是如何通过量化评价传感器之间的冗余度以获取传感器配置集合的帕累托最优解，从而达到测点传感器在位置和数量上的最优。

关于系统解析冗余度分析的研究近年来也很受关注。传递熵是由Schreiber于2000年基于信息熵的基础上提出的，它能够量化两个序列之间的信息传递，进而判断两个变量时间是否存在因果关系。通过这一方法，可以消除变量之间的冗余关系，起到对模型简化的目的。在工业过程控制中，文献[16]在化工领域借助传递熵建立了控制变量之间的因果关系，并通过构建因果图达成操作变量变化的成因分析。以此为基础很多学者对传递熵算法进行了改进，如文献[17]提出一种基于传递熵的非线性系统序列预测模型，借助因果关系进行了辅助变量的设计和冗余度的消除。文献[18]利用传递熵方法将工业机器人中的故障隔离问题视为耦合动态过程中的因果分析问题，进行基于因果关系的故障溯源，取得了较好的效果。在传感器冗余度消除方面，文献[19]提出了一种基于传递熵的管网泄漏事件识别优化框架。文献[20]研究一种基于传递熵的传感器布局方法，并深入分析了测量噪声和模型误差对传感器布局的影响。文献[21]针对电源车进行了基于故障可诊断性的传感器优化配置，但优化指标单一，且未考虑传感器之间的冗余特性。

作为提高军队野外作战能力的重要设备，基于信息化与智能化技术，对电源车进行全生命周期诊断、预测与健康维护已是未来发展的趋势。然而这些能力的实现都要以配置足够数量的传感器为前提，在空间有限和部分传感器配置经济成本过高的现状下，实现电源车传感器的优化配置就显得尤为迫切，目前此项研究还在起步阶段。

鉴于此，本文在混合信息熵指标约束下进行传感器的优化配置，其中混合信息熵指标包括信息值量化指标和传递熵量化指标，首先，利用信息值方法量化评价电源车常见故障的可检测性和可隔离性的测点传感器集合，涉及的电源车故障类型包括调速器故障、励磁系统故障、发电机失磁、系统超载等；其次，借助传递熵方法量化评价测点传感器的冗余度，并进而通过优化减小冗余度，以达到对测点传感器优化配置的目的。

1 基于传感器信息值的故障可诊断性量化评价

1.1 传感器信息值理论研究

设电源车的测点传感器为,,…,，其测量数据为,,…,，其中为测点传感器的数量。对于系统中可能发生的某一故障，其数学模型表述为

=

(1)

式中：为故障序号，∈；为故障幅值的变化序列；若当前故障为加性故障，则为由故障引起的传感器偏置，若当前故障为乘性故障，则∈(0,1)。

(2)

当系统正常运行时，传感器的残差数据通常较小，且在0值范围内波动，可以估计出它的先验概率密度函数为()。当系统发生故障时，故障信息在系统内传播，某一传感器获得故障信息时，对应的测量数据可能会发生变化。然而，是否变化取决于故障信息与该传感器之间是否存在因果关系，采用贝叶斯公式可以推断这一关系：

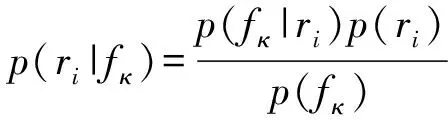
(3)

式中：(|)为在故障的影响下，新的传感器残差概率密度函数值；(|)为条件概率，即当残差数据为时发生故障的概率；()为故障发生的概率。

故障的作用下，会使得先验概率密度()增强或是无变化，这取决于故障对第个传感器的影响力。定义传感器的信息值为故障发生前后传感器残差数据的概率密度函数之差，其反映的是条件概率是否会增强先验概率。考虑故障信息的有效性，可以定义故障发生后和发生前信息接收的有效性函数分别为

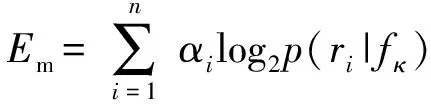
(4)

(5)

式中：为代价因子，若故障与传感器直接相关，则因子应该被加强，否则弱化。

传感器是否能够有效检测故障，关键在于残差是否会受到故障的影响，即和差值有多大。可借助传感器的信息值来量化故障对传感器数据的影响：

(6)

为简化计算，并进一步揭示(6)式对于传感器信息值所蕴含的物理意义，引入如下定理来分析说明。

对于有个测点传感器,,…,的系统，若系统发生故障，则某一测点传感器残差的信息值为

=((|)‖())

(7)

式中：=()(|)；((|)‖())为概率密度函数之间的相对熵，即K-L散度。

对于单个传感器残差数据，其信息值为

=(){log[(|)]-log[()]}

(8)

对(8)式进行变换，可得

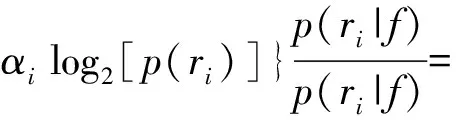
对于有个测点传感器,,…,的系统，若系统发生故障，则全部测点传感器残差的信息值为

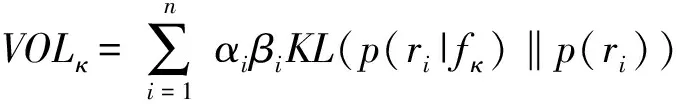
(9)

相对熵，又被称为K-L散度，是两个概率分布和间差异的非对称性度量，具有如下特性：

(10)

1.2 基于传感器信息值的故障可诊断性量化评价

通过11节的证明可见，传感器的信息值可以转化为计算先验概率密度与后验概率密度之间的K-L散度。若故障与当前配置的传感器集合存在因果关系，则故障的发生必然会导致信息值的变化。图1所示为电源车发生调速器故障时，在系统 8个传感器测点处检测到的信息值柱状图，将其拟合为一条曲线(见图2)，其中选取的8个测点传感器分别检测的信号有：电压、电流、机体温度、功率因数、频率、负荷、发动机转速及励磁电压。

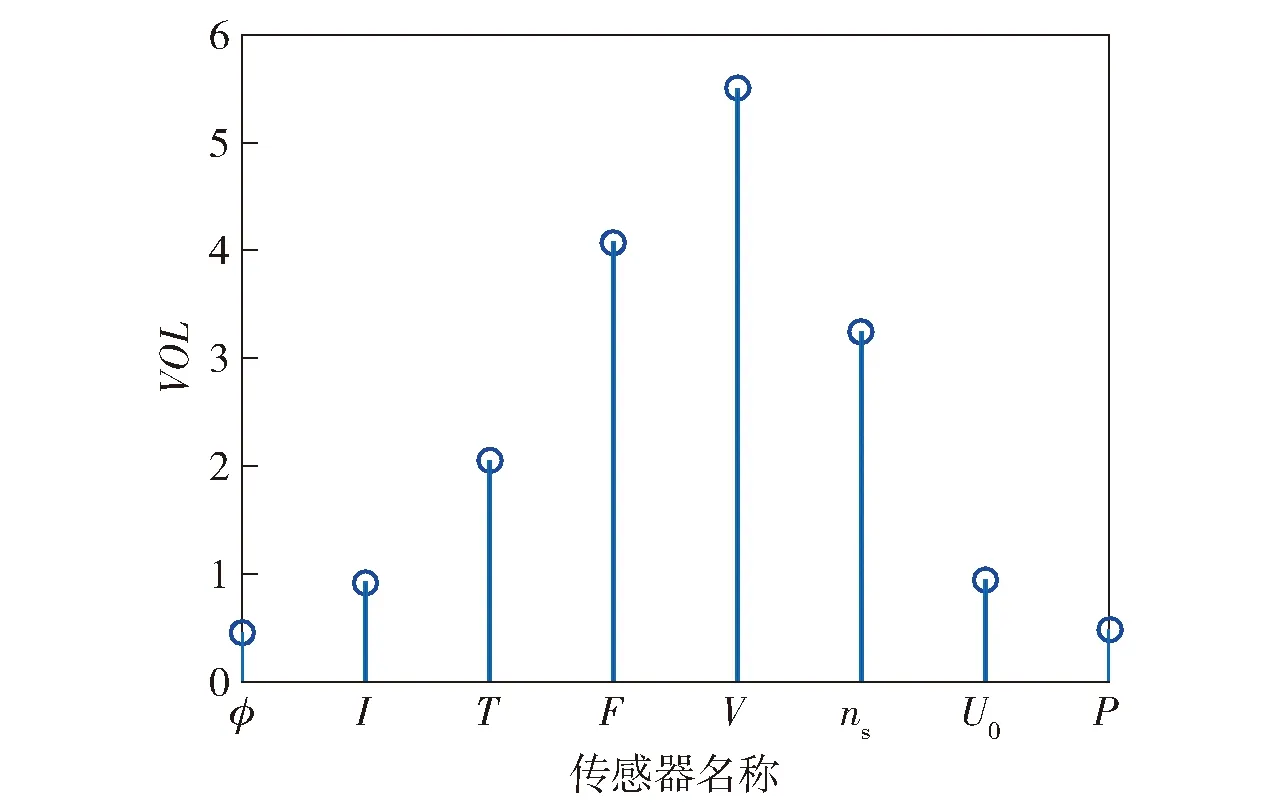
图1 传感器信息值柱状图Fig.1 Bar chart of sensor information values

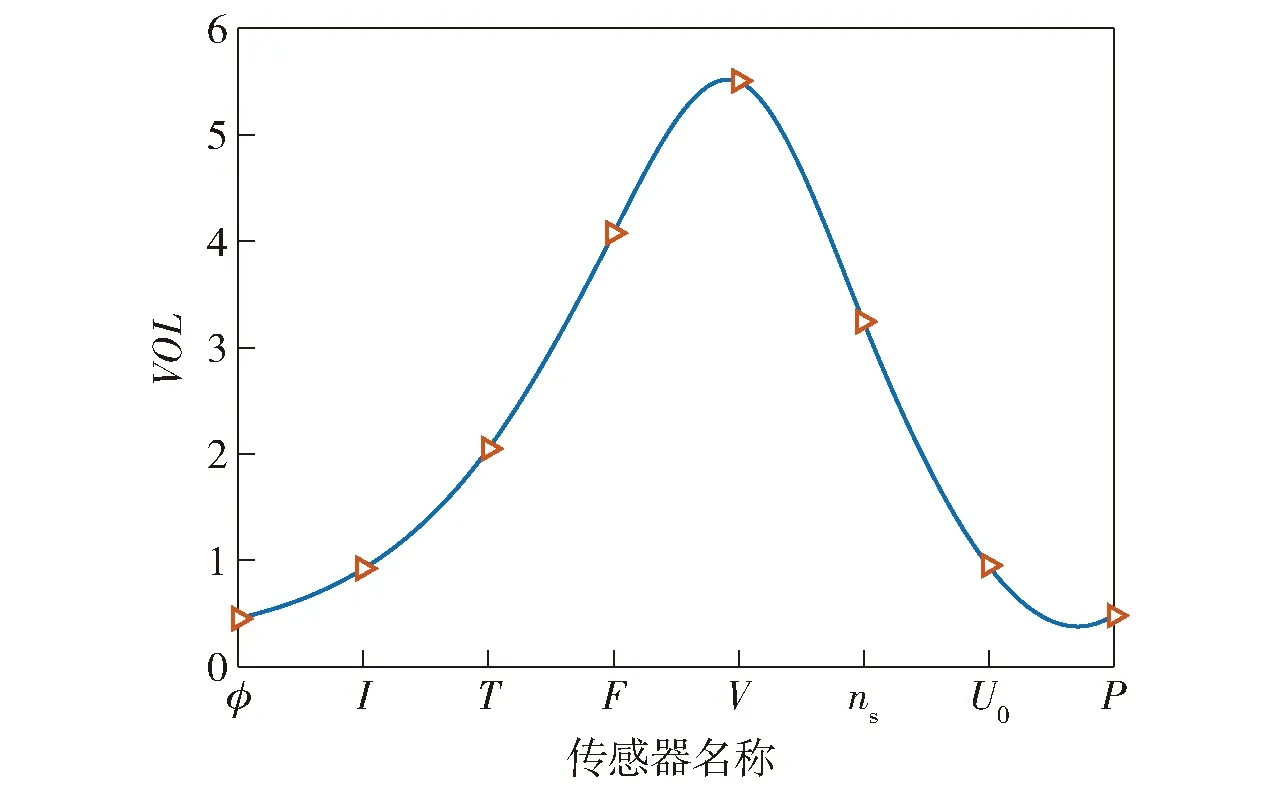
图2 故障fκ下的传感器信息值示意图Fig.2 Schematic diagram of sensor information value under fault fκ

在离散情况下，图1中横坐标为选取的8个测点传感器，纵坐标为各个测点传感器节点的信息值。在数据连续的情况下，图2中曲线与横轴形成图形的面积为当前传感器的信息总值，即所有测点的信息值之和。两种概率密度函数和的K-L散度最小化等同于这两种概率密度函数的最大似然估计，因此，可将故障的可检测性量化指标定义为

()=min ()

(11)

(11)式中的最小化指的是故障幅值最小时的信息值，若故障幅值最小时满足可检测性，则故障在变化过程中均满足可检测性要求。

由此可得传感器的配置目标之一是：优化配置系统传感器，使得系统对任意故障满足可检测的基本指标要求，即满足：

()>

(12)

式中：为可检测量化指标的阈值。

当系统配置足够多的传感器时，故障可检测性会显著提高。然而，由于传感器成本和安装可实现性的限制，需在满足可检测性最低指标要求的基础上，优化传感器配置的数量和位置，使得传感器有最大的故障覆盖面。

当电源车可能发生的故障有两种时，即电源车调速器故障和励磁系统故障，假定这两种故障均具有可检测性，为了对两种故障进行隔离，就需要比较二者之间的信息值。图2和图3分别为故障和对应的传感器集合信息值变化示意图。

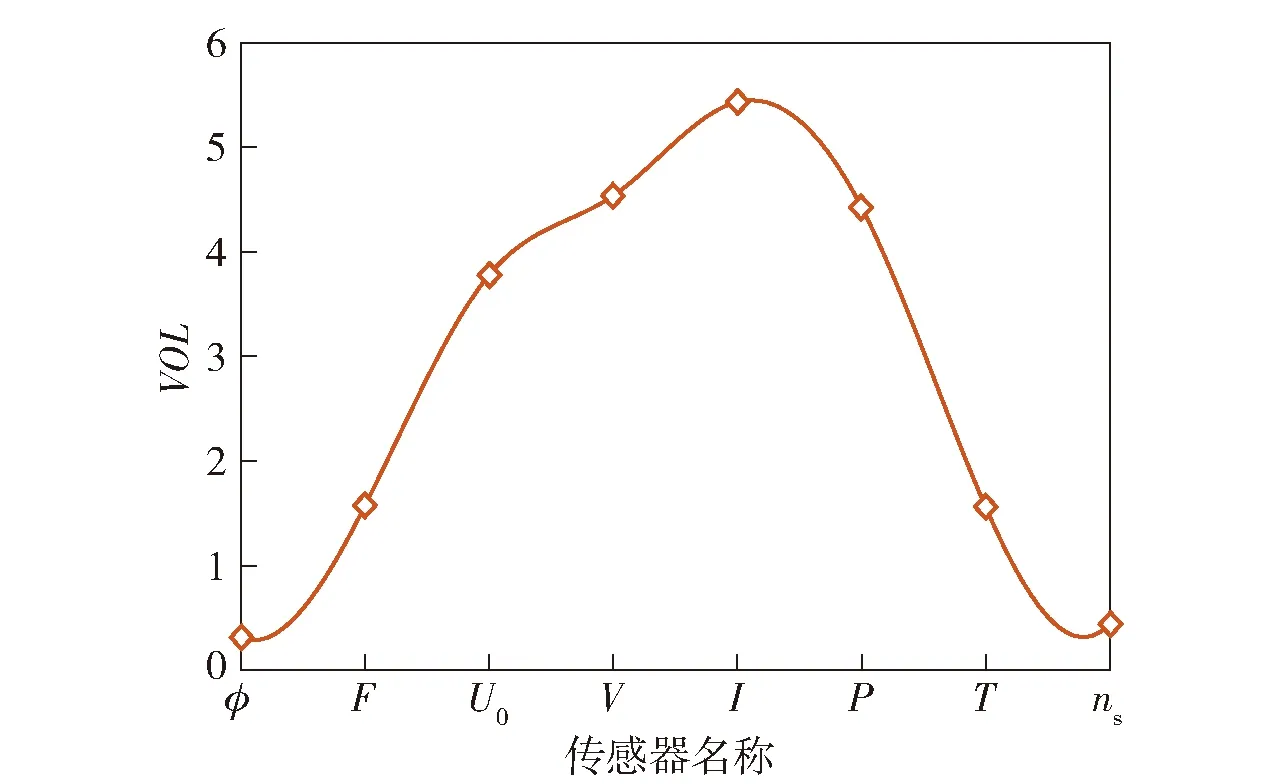
图3 故障fυ下的传感器信息值示意图Fig.3 Schematic diagram of sensor information value under fault fυ

图2和图3中信息值是针对故障和的特定幅值绘制的信息值曲线，如果将曲线包围面积作为故障可隔离性的评价指标，可以确定两种故障之间的可隔离性量化评价结果。然而，在实际工程中，故障幅值不会是单一的，不同的工况可能面临不同的故障幅值。因此，两种故障的可隔离性应该考虑故障幅值的全范围覆盖。图4和图5分别为故障幅值变化时和的信息值曲线。

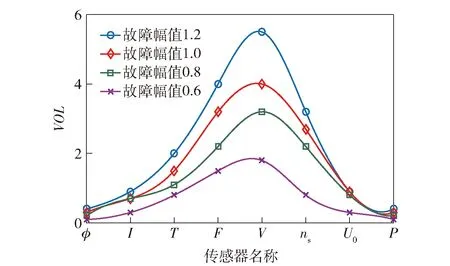
图4 不同故障幅值下的信息值曲线(故障fκ)Fig.4 Information value curve under different fault amplitudes (Fault fκ)

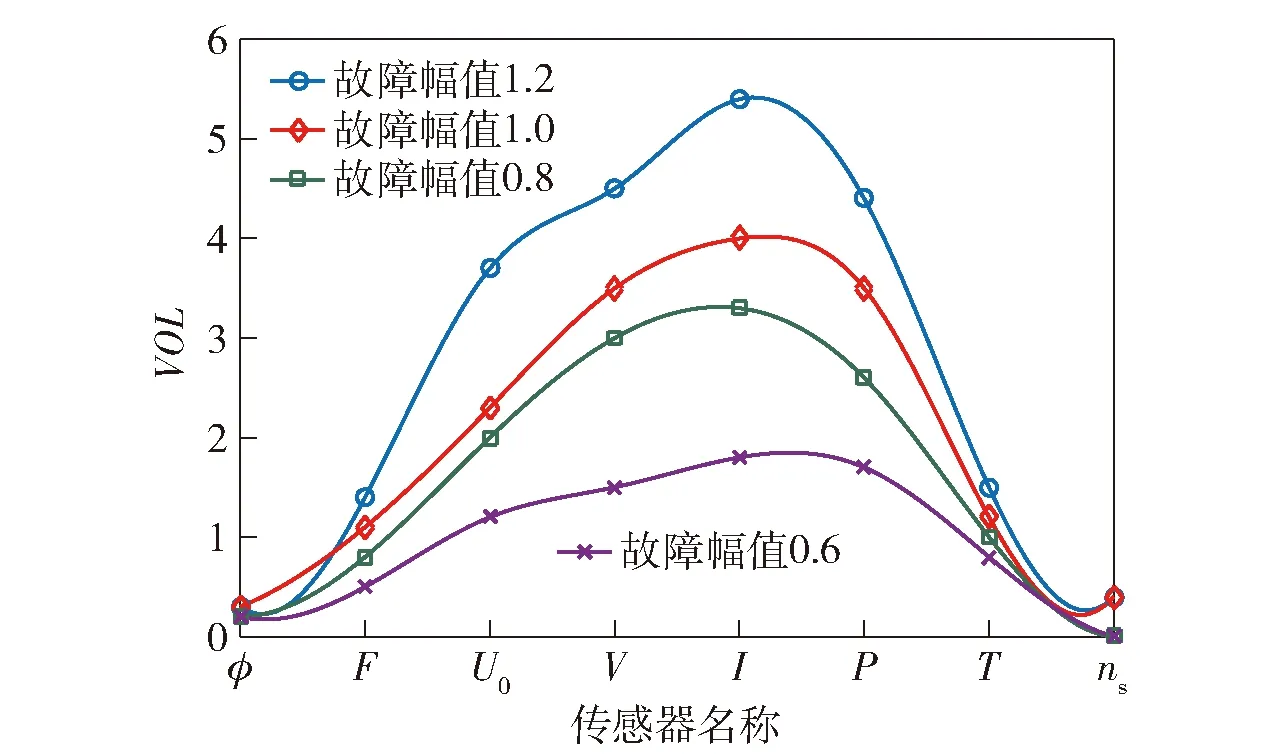
图5 不同故障幅值下的信息值曲线(故障fυ)Fig.5 Information value curve under different fault amplitudes (Fault fυ)

从图4和图5可以看出，当故障幅值变化时，传感器集合的信息值也会相应的发生变化，当故障幅值大时，信息值比较大，当故障幅值变小时，传感器信息值相应地变小。为了更全面地描述不同故障幅值对信息值的影响，进而量化评价两种故障的可隔离性，将可隔离性量化指标定义为

(,)=min [E()-E()]

(13)

其中：E(·)代表期望函数。

由于故障诊断传感器配置目标不仅要使得故障满足可检测性，还应该使得不同故障之间满足可隔离性，这对传感器的配置提出了更高的要求。

2 基于传递熵的传感器冗余度评价

即使是不同的传感器配置集合，也可能有相同的信息值，主要原因是集合内的传感器存在冗余。传感器优化配置的基本要求是：传感器集合要全面地覆盖系统故障，且互相之间的冗余度要尽可能小。这就需要对传感器之间的冗余度进行量化评价，选取冗余度最小的传感器配置集合，降低系统运行的成本。

定义彼此相关联的传感器共有的信息为互信息，用以量化测量数据之间的共同信息：

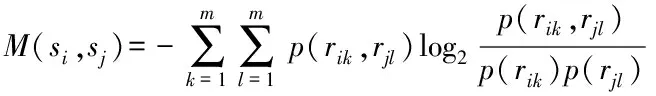
(14)

式中：(,)为传感器和的互信息；为残差数据的状态数；(,)为传感器残差和的联合概率密度；()和()分别为残差和的概率密度。

互信息表征了两个传感器共同传递的信息，但是无法表示传感器之间传递信息的方向，在互信息的基础上，认为传感器向传递的信息是：和共同向未来传递的信息减去自身传递的信息，记为传递熵。它是互信息和条件熵共同作用的结果，传递熵的定义为

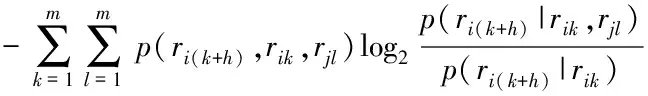
(15)

式中：为传感器数据的预报范围。通过对的调节可以使传递熵适应变量间不同的延迟，更加符合实际情况。

两个传递熵的差可以用来表示传感器数据之间的因果关系：

→=(+|,)-(+|,)

(16)

如果→>0，表示传感器对的影响比对的大，此时是导致变化的原因，是造成的结果。相反的，如果→<0表示是变化的主要原因。如果→接近为0，则表示两个变量没有明确的因果关系。因此，本文采用传递熵来量化评价传感器之间的冗余关系：

|1-→|>

(17)

式中：为冗余度量化评价的阈值。若(17)式成立，则意味着两个传感器数据之间存在冗余，可以约简是“结果”的传感器，保留是“原因”的传感器。这样就可以在保障电源车传感器之间较小的冗余度，降低系统的运行成本，满足安全性与经济性需求。

3 传感器的多目标优化过程

通过上述分析可以看出，电源车系统传感器的优化配置是一个集传感器数目、故障可检测性、故障可隔离性以及冗余度的多目标的优化问题。该优化问题可描述为

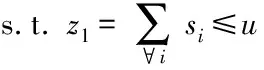
(18)

=()>

(19)

=(,)>

(20)

=|1-→|>

(21)

式中：为传感器数量上限；为可分离性量化指标的阈值。

约束条件分别为传感器总数、故障可检测性量化评价指标、故障可隔离性量化评价指标和传感器冗余度量化评价指标。在满足这些约束条件的前提下，寻求最优的电源车测点传感器集合，使其在位置和数量上达到最优。

对于多目标的优化问题，可以采用改进的非支配排序遗传(NSGA-II)算法进行优化求解。NSGA-II算法作为一种比较优秀的多目标优化算法，借助于快速非支配排序可降低算法的计算复杂度，通过增加拥挤度和拥挤度比较算子，保持种群的多样性，还采用精英保留策略维持了扩大了采样空间，使得最佳个体不会丢失，迅速提升了种群水平，达到对多约束条件、多目标函数进行综合优化目的。NSGA-II算法对电源车传感器的优化配置算法如下：

1) 随机生成一个初始种群，对初始种群进行非支配排序，并选择适应度高的个体进行、交叉、变异操作，生成子代种群，此时=0；

2) 合并父代和子代种群，=∪，对种群进行快速非支配排序；

3) 对中每个非支配帕累托等级的个体进行拥挤度排序，根据支配关系和拥挤度关系选择最优的个体，形成新的种群+1；

4) 借助于选择、交叉、变异操作得到子代种群+1；

5) 判断是否满足终止条件，若满足则终止循环，否则回到步骤2。

传感器优化的具体过程如图6所示。

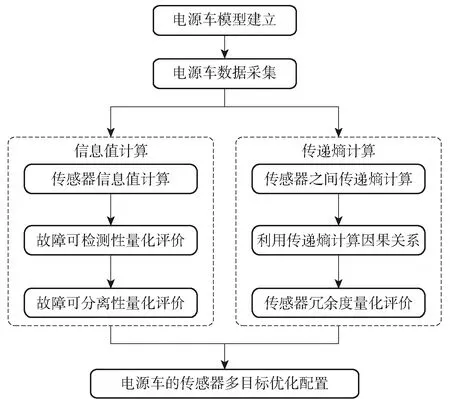
图6 电源车传感器多目标优化配置流程Fig.6 Multi-objective optimization configuration of the power vehicle sensor

4 仿真实验分析

4.1 电源车系统和常见故障描述

这里以某电源车设备厂商的120 kW电源车为研究对象，该设备可提供120 kW的额定输出功率，输出电压为400 V。电源车的硬件设备包括：用于支撑的汽车底盘、提供动力来源的柴油发电机系统、励磁系统和电子调速器等，各模块之间的关系如图7所示。

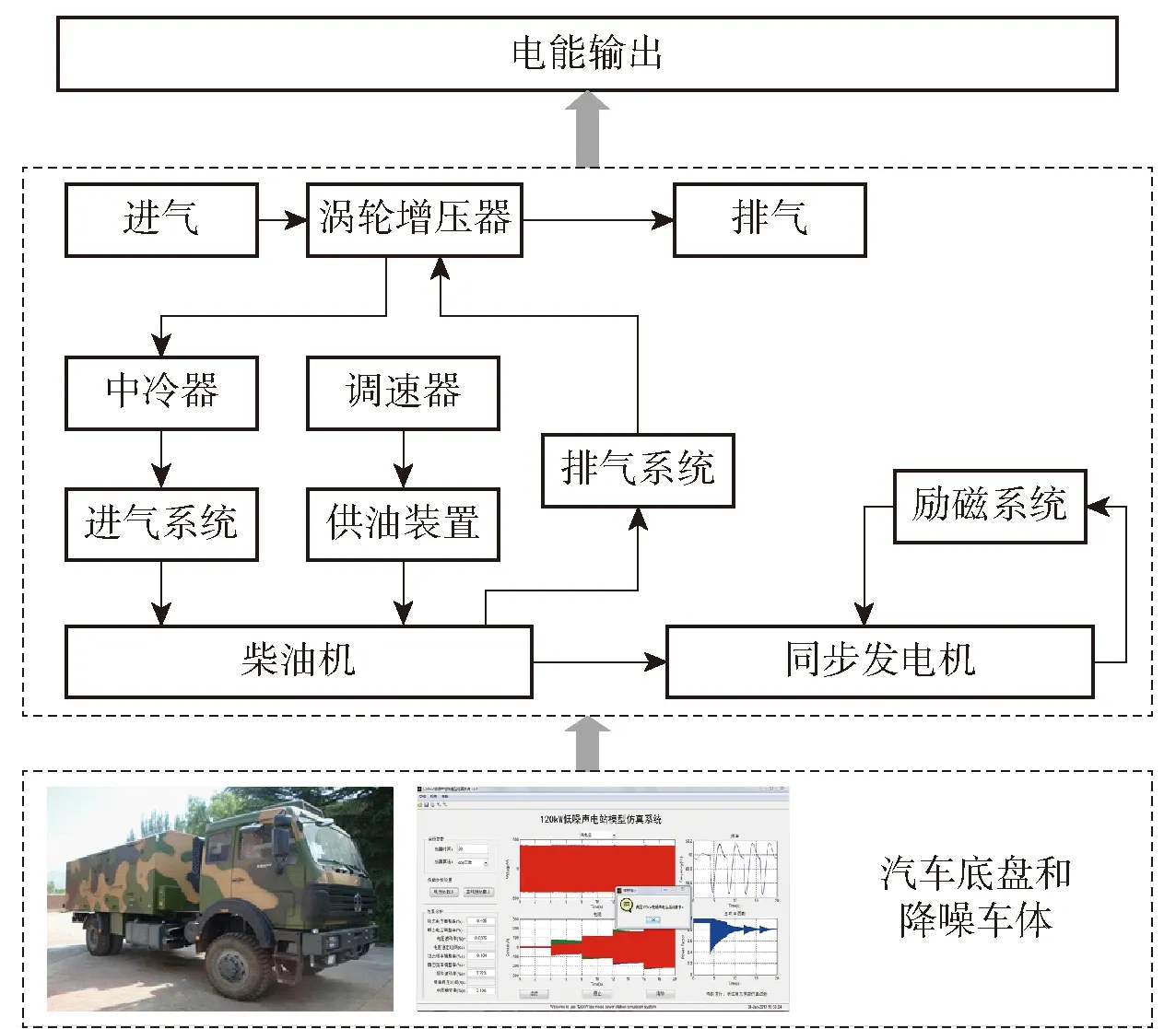
图7 电源车结构图Fig.7 Structure diagram of power car

本仿真实验所采用的数据来源于与该电源车设备厂商联合开发的120 kW车辆电源仿真系统，该系统开发于2014年，已完成现场测试。此系统借助模块化的方式对电源车系统进行建模，将电源车模型分解为柴油机模型、同步发电机模型、调速器模型、励磁系统模型和负载模型。本文所有的数据均为仿真系统采集的数据，各模块之间的关系如图8所示。

图8 电源车模块关系图Fig.8 Schematic diagram of the power vehicle modules

图8中，向量为发电机轴和轴电压，为发电机轴和轴电流，励磁电压，为发电机机械功率，为发电机转速，发电机的额定输出电压为400 V。表1为车辆电源系统运行过程中常见的一些故障类型。

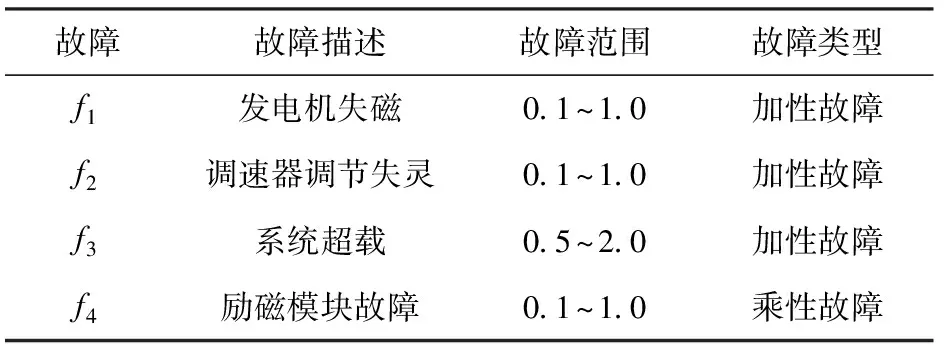
表1 车辆电源常见故障描述

表1中故障范围为电源车部件偏离正常运行值的变化范围，由于电源车系统中状态值通常都采用标幺值表示，因此故障范围为基于标幺值的变化量。电源车在长期运行过程中故障类型众多，统计显示表1中所示的4种故障发生频率较高，为使本文中传感器的优化配置方法具有现实可操作性，在仿真过程中只考虑这4种故障情况，故障范围是为了符合实际对象运行情况仿真模拟的故障数值。可见，要检测和隔离这4种故障，就需要在合适的位置配置与故障关联的传感器。在对所需传感器数量和位置配置情况未知的前提下，先列出电源车所有可能配置的测点传感器，再通过信息值方法确定满足故障可检测性和可隔离性需求的测点传感器集合。选取电源车可能配置的8个测点传感器、、、、、、、，即电压、电流、机体温度、功率因数、频率、负荷、发动机转速及励磁电压。该电源车系统中传感器优化配置的要求是，要使的电源车常见的4种故障情况均具备可检测性和可隔离性。

4.2 电源车故障可诊断性量化评价

根据本文中基于信息值的故障可检测性量化评价方法，配置不同数量的传感器时，故障检测的量化评价指标也是不同的。为确定评价指标的敏感性，每一种故障要选取故障发生时幅值的最小值。所得的信息值与传感器配置数量的关系如图9所示。

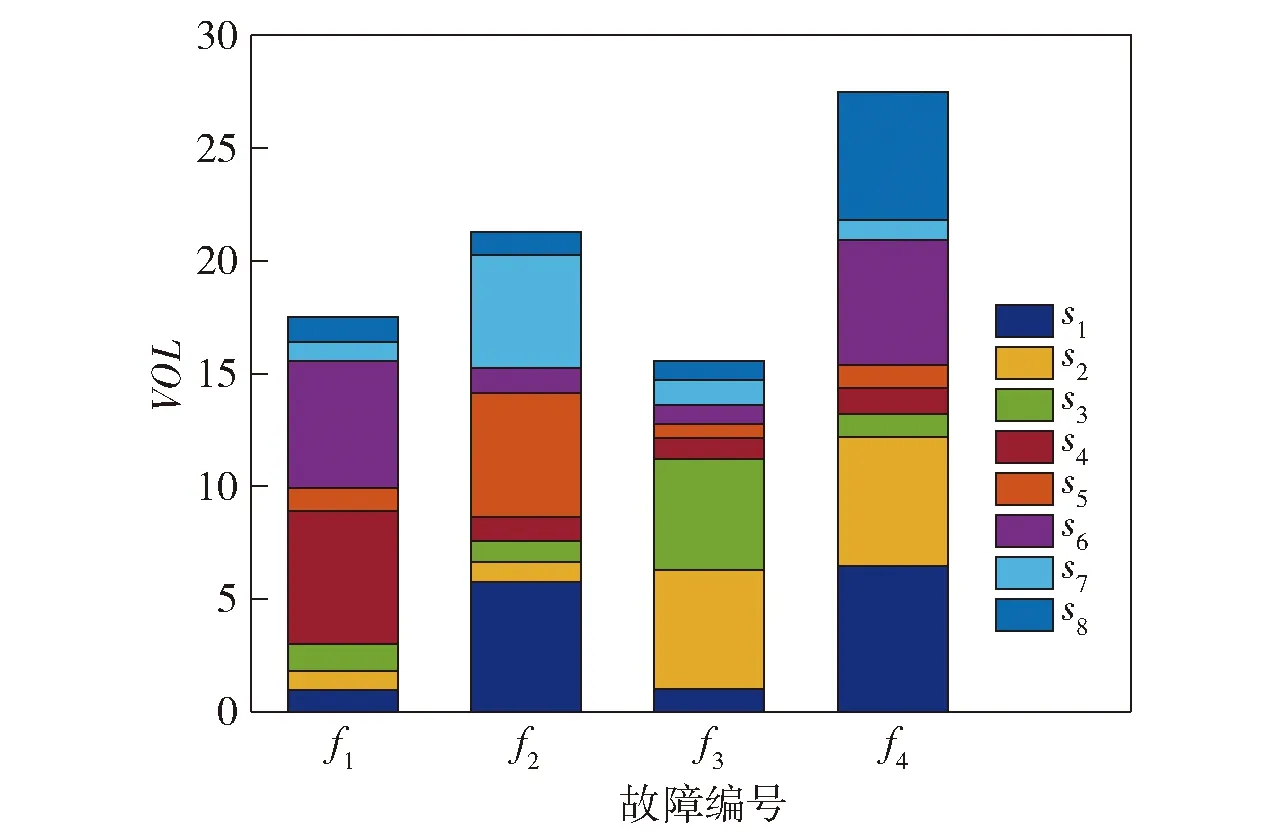
图9 不同传感器对应的信息值变化Fig.9 Simultaneous interpretation of sensor information

在图9中，横坐标代表4种不同的故障情形，纵坐标为传感器集合的信息值，图形中8种不同的颜色由下到上，依次代表8个不同的传感器。例如当故障发生时，传感器和的信息值变化较大，其余传感器的信息值变化较小。因此，要实现对故障的检测，就要从传感器集合{,}中选择子集来配置。同理，对于故障而言，传感器、、、的信息值变化较大，其余传感器信息值变化小，对于故障的检测，就要从集合{,,,}中选择子集来配置。

通常而言，传感器配置的数目越多，故障的可检测性量化评价指标越大，如图10所示。

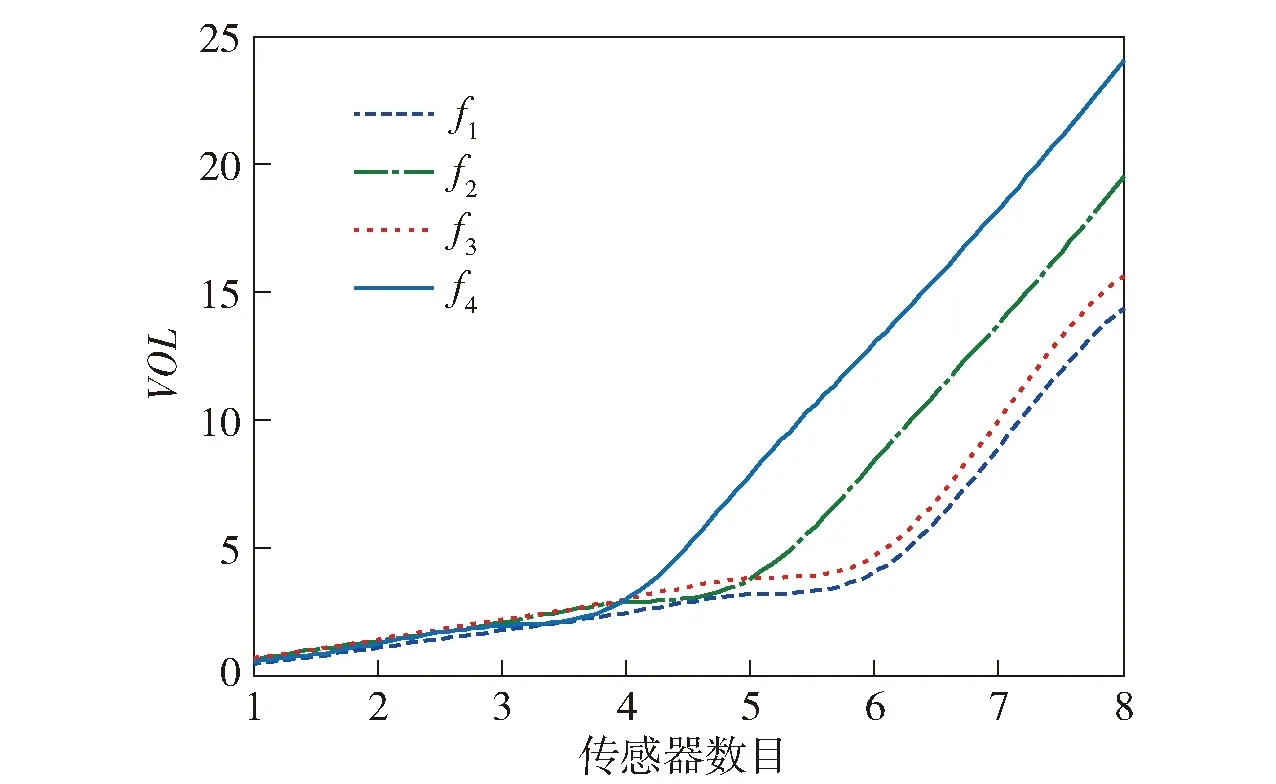
图10 传感器配置数量与故障可检测性关系图Fig.10 Relationship between the number of sensors and fault detection capacity

从图10可以看出，当传感器配置数量逐渐增多时，传感器集合的信息值增大，4种故障的可检测性量化评价指标也随之增大。

在保障了故障可检测后，还需要评价4种故障之间是否可以被隔离，故障隔离通常要比故障检测复杂。对于表1中的4种故障，当配置了所有的 8个测点传感器时，通过本文方法，可计算故障之间可隔离性的量化评价结果如表2所示。

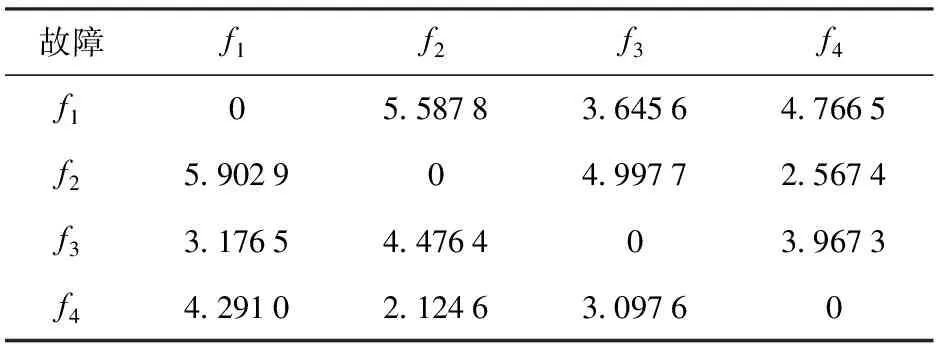
表2 故障可隔离性量化评价

从表2可以看出，当电源车配置了8个传感器时，表1中的4种故障均可以被隔离。事实上，考虑传感器配置的经济性和可实现性，对这4类故障的诊断，也可能无需配置所有的传感器，而是从这8个传感器中选择部分进行配置，就可以得到对所有故障进行检测和隔离的目的，对电源车传感器的优化配置可以实现这一目标。

4.3 电源车传感器的多目标优化配置

前面的分析过程中，只是单独考虑了满足故障可检测性或是可隔离性时的传感器配置，而实际的传感器配置过程是一个综合优化的过程，优化的目标是要用最少的传感器来达到最佳的故障可诊断性评价指标要求，这就需要在配置过程中精简传感器配置数量，剔除传感器配置集合中的冗余测点。为了达成这一目的，还需进一步分析传感器之间的冗余度，如图11所示。

图11 传感器之间的冗余度分析Fig.11 Analysis of redundancy between sensors

图11中横坐标为传感器集合{,,…,}之中的传感器两两配对，即{,|<,=1,2,…,8,=1,2,…,8}，当冗余度指标超过阈值就意味着两个传感器之间存在冗余，可得存在冗余度超过阈值的传感器集合为{,}、{,}、{,}、{,}。

图11中的阈值是借助文献[23]中的方法设计的。首先，选取一组弱相关的传感器运行数据，如和；其次，根据冗余度量化指标的分布特性实现阈值的设定，可得阈值为=(±217)，其中和分别为两个弱相关传感器冗余度指标的均值和方差，为放大因子，∈[12，15]。综合电源车的故障可检测性、可隔离性量化评价指标及冗余度量化评价指标，借助于NSGA-II算法求解多目标优化配置问题，可得电源车要配置的传感器集合为{,,,}。在系统配置这4个传感器时，对常见故障的可检测性和可隔离性分析如表3所示。

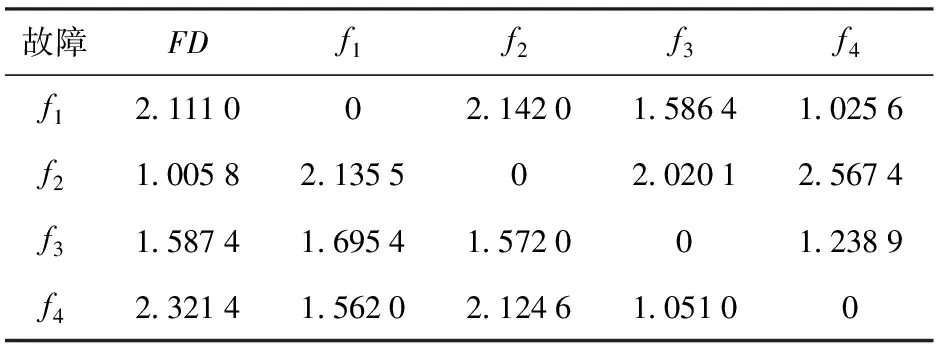
表3 故障可诊断性量化评价

表3中为优化后的传感器配置集合下电源车常见故障的可检测性，其余列为不同故障之间的可隔离性。这里定义故障可诊断性量化评价的阈值为=09，可以看出，在传感器优化之后4种故障依然满足可检测性和可隔离性的评价要求。此时，所有的4种故障均可以被检测且可以被隔离，满足传感器优化配置的指标要求，也就是电源车要满足表1中4种故障的可诊断性时，最佳的传感器配置为电压传感器、电流传感器、机体温度传感器和频率传感器。

5 结论

本文提出一种基于混合信息熵约束下的电源车传感器优化配置方法，量化评价指标主要包括故障可诊断性评价指标和传感器之间的冗余度评价指标。其中故障可诊断性评价选用了基于信息值的方法，即通过衡量故障影响下传感器残差后验概率值的变化，来获取传感器集合信息值的变化，以此为依据得到使得电源车故障序列可被检测的传感器配置集合。同时对传感器之间存在的冗余信息，采用传递熵方法进行评价，在得到传感器之间的冗余度的同时，获取信息传递的因果关系。最后，通过多个量化指标约束下的多目标优化配置方法获得传感器配置数量和位置的最优解。

此项研究是与某电源车辆研究所联合开展的，旨在提升电源车远程诊断和运行维护能力。通过对设备运行的长期观测，已经拥有一定量的故障数据基础，但目前研究的局限性在于电源车传感器配置数量有限。虽然目前可以对常见故障进行顺利检测，但在故障的可隔离性研究方面还需进一步深入。因此，下一步的研究内容将集中在对观测数据的相关性、因果性分析，以及如何通过配置软传感器提升电源车系统的可靠性方面。