基于高斯混合- 隐半马尔可夫模型的双侧独立电驱动无人履带机动平台纵向决策方法

刘庆霄， 唐泽月， 张超朋， 刘海鸥， 陈慧岩

(北京理工大学 机械与车辆学院, 北京 100081)

0 引言

无人驾驶车辆是多领域科学技术的集成运用平台，在众多方面有着潜在的应用价值。同时，基于双侧独立电机的分布式电驱动技术依靠其结构紧凑、动力性强等优势，加速了履带机动平台电动化、无人化的发展进程。其中，纵向速度决策是电驱动无人履带机动平台研究领域的关键问题之一。以车辆直驶过程中遇见障碍物并低速靠近障碍物的行驶工况为例，在加速过程中，纵向决策系统需要根据平台加速度特性将加速度平衡在高效、安全的区间内，以提高车辆的灵活性；在制动过程中，纵向决策系统需要根据制动需求设计合理的制动行为，保障平台的安全。同时，地面条件与平台驱动电机响应的不确定性也大大增加了纵向决策系统的设计难度。

为了获得履带机动平台在纵向行驶过程中的行驶特性，一些学者在平台运动学与动力学模型构建方面展开了大量的研究工作。孙逢春等建立了履带平台行动部分动力学模型，并提出牵引电机控制方法，在实车试验和仿真中验证了其加速特性。陈朝萌等在电驱动履带平台动力学模型基础上，提出基于滑膜鲁棒控制、制动扭矩预分配规则的机- 电- 液联合制动防抱死策略，将平台滑移率控制在合理范围内。针对4个以上驱动电机的过驱动系统，曾庆含等结合履带平台运动学与动力学分析，制定电机转矩优化分配策略，提高了动力输出稳定裕度。文献[2-4]均建立了完备的电驱动履带平台动力学模型，并对电机控制特性进行了深入的研究工作，但这些研究缺乏在真实越野环境中的试验验证，且忽视了驾驶员操控平台纵向性能的影响。刘瑞等利用庞大的驾驶数据库探讨了驾驶员加速度分布的收敛性与分布特性。沈沛鸿等利用基于自适应网络的模糊推理系统设计纵向驾驶员模型，试验结果表明其决策得到的油门踏板行程、挡位和需求转矩接近于实车试验结果。在Qu等对驾驶员行为的研究中，为反映驾驶员对车辆运动特征的感知，在决策模块中基于车辆动力学生成期望最优加速度。Qu等提出一种适用于轮式车辆的基于模型预测控制(MPC)的多模式切换纵向自动驾驶系统。为提高纵向运动平顺性，Seina等在试验车辆制动模型的基础上采用线性二次型(LQ)最优控制方法建立了驾驶员制动模型，仿真试验验证了驾驶员模型对提高平顺性的作用。为提取影响驾驶安全的变量因子，Peng等基于改进后的变精度粗糙集模型建立车- 路- 人闭环系统的数据挖掘模型，为预警系统提供了更精确的评估结果。为了提高驾驶员模型在公路上与其他车辆的交互性，Tian等建立了基于车辆- 道路交互行为的交互多模型(IMM)，该方法在仿真实验中表现出了对周围动态环境良好的适应能力。

随着机器学习方法在自动驾驶领域的广泛应用，具有学习能力的驾驶员模型得到了广泛的研究。Dimitrios等通过大量的驾驶数据训练了6种线性回归模型，用于预测不同行驶条件下的平均行驶速度，有利于构建精细的驾驶员速度模型。为提高学习型驾驶员纵向模型的适应能力，Lu等提出基于强化学习算法的类人速度决策系统，该系统在仿真环境和实车试验中得到了验证。针对重型车辆驾驶员，Mumcuoglu等提出基于长- 短时记忆(LSTM)的纵向驾驶行为模型，用于评估驾驶员的危险加速和制动行为。Wang等使用高斯混合模型(GMM)和隐马尔可夫模型(HMM)对驾驶员跟车行为进行建模，该方法有效地辨识出了驾驶员的制动意图。Liu等提出隐半马尔可夫模型(HSMM)，对基于GMM-HMM的驾驶员模型进行了优化。基于GMM-HMM的驾驶员模型同样适用于履带车辆驾驶员建模。王博洋等基于GMM-HMM驾驶员模型实现了履带平台横纵向协同跟踪控制，有效地利用驾驶员的经验解决了横纵向控制的强耦合性和不确定性。文献[5-16]中的研究对象均为城市环境中的轮式车辆及其驾驶员，环境不确定性以及干扰较少。文献[17]验证了基于GMM-HMM的驾驶员模型在越野环境及履带平台上的有效性，但研究内容没有突出驾驶员纵向操控过程。

综上所述，各国学者在电驱动履带机动平台行动部分动力学建模与轮式车辆驾驶员纵向行为建模领域均取得了丰富的研究成果。但是针对双侧独立电驱动的履带机动平台类人纵向决策的研究还较少，如何结合电驱动履带车辆的行驶特性与驾驶员决策行为，设计不依赖精确地面参数与车辆参数的纵向决策系统是本文研究的关键问题。

本文基于驾驶员模型对双侧独立电驱动无人履带机动平台纵向决策过程展开研究工作。采集驾驶员在真实越野环境中直驶的操控数据与车辆状态，并在道路末端设置垂直墙模拟制动工况。通过GMM从当前车速和与障碍物间距中得到驾驶员的行驶意图，并利用高斯分布学习驾驶员在某一期望速度上的持续时间，在此基础上基于HSMM生成驾驶员的纵向决策结果。该系统在不同地面条件(干燥土路与泥泞土路)上均通过了实车验证。试验结果表明，通过控制状态持续时间可以有效地模拟熟练驾驶员依靠体感进行纵向决策的驾驶行为特性，同时不依靠于准确地面参数与车辆参数将平台加速度控制在合理区间内。

1 双侧独立电驱动履带实验平台

图1 电驱动无人履带机动平台感知定位系统Fig.1 The perception and location system of the electric unmanned tracked platform

为了实现无人履带机动平台类人纵向决策系统验证，搭建了如图1所示的双侧独立电驱动履带机动平台无人系统，其中激光雷达、相机构成了环境感知系统，惯导、GPS构成了组合导航定位系统，以及车载计算单元构成了运算处理系统。如图2所示，装置在两侧的独立驱动电机为履带机动平台提供车辆驱动动力，驱动电机与主减速器之间装备了两挡行星自动变速器。车辆的动力能源来自车载高压电池组和增程式发动机发电机组。双侧独立电驱动无人履带机动平台的具体车辆参数如表1所示。

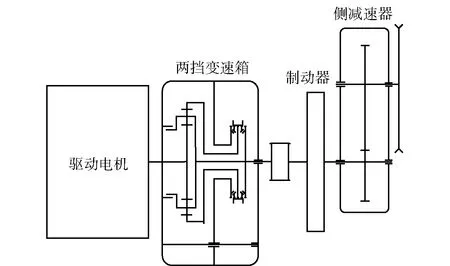
图2 无人履带机动平台电驱动系统Fig.2 The electric drive system of the unmanned tracked platform

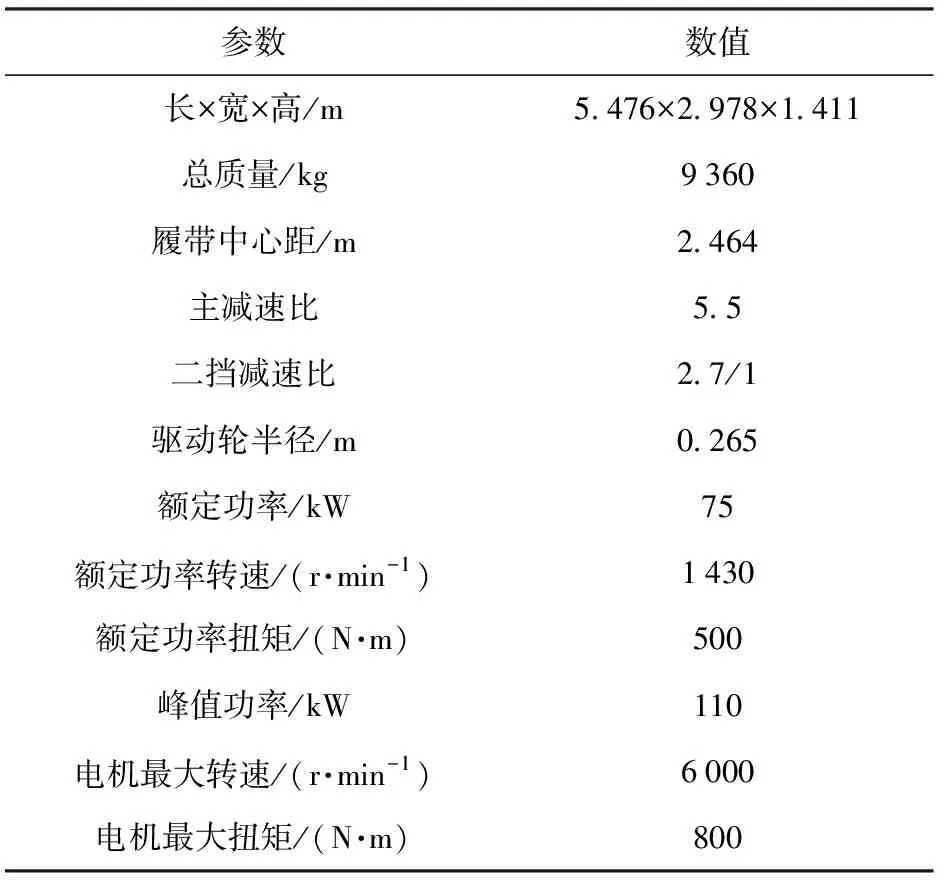
表1 无人履带机动平台重要参数

2 双侧独立电驱动无人履带平台类人纵向决策系统

由于履带机动平台在越野环境中面临多种任务需求，驾驶员需要在加速或制动过程中充分保证平台灵活性与安全性，以及满足基本的舒适性要求，即控制平台纵向加速度在合理的区间内。过大的纵向加速度值增大了无人平台转向的难度，而过小的纵向加速度值则降低了平台行驶效率与制动过程的安全。本文从驾驶员纵向操控行为出发，通过模拟驾驶员在不同地面条件下的操控行为，实现双侧独立电驱动无人履带类人平台纵向速度决策。

驾驶任务主要分为4个部分，分别是加速至最大期望速度、恒速行驶、发现障碍物后开始制动以及缓速接近障碍物。试验路面包括平坦的干燥土路和平坦的泥泞土路两种。研究流程框图如图3所示，首先将车载传感器采集到的驾驶员操控数据、平台状态和环境信息处理成可用驾驶数据集，该数据集用于训练驾驶员纵向决策模型参数。在训练后的纵向决策模型基础上，利用障碍物识别与测距算法获得模型输入，基于GMM方法辨识4种驾驶意图(驾驶子任务)。该意图作为隐藏状态参量输入HSMM，根据持续时间和转移规律模拟驾驶员的决策转移过程，从而生成具有驾驶员操控特性的平台期望速度。下面将详细阐述驾驶员纵向决策模型建模与学习方法。

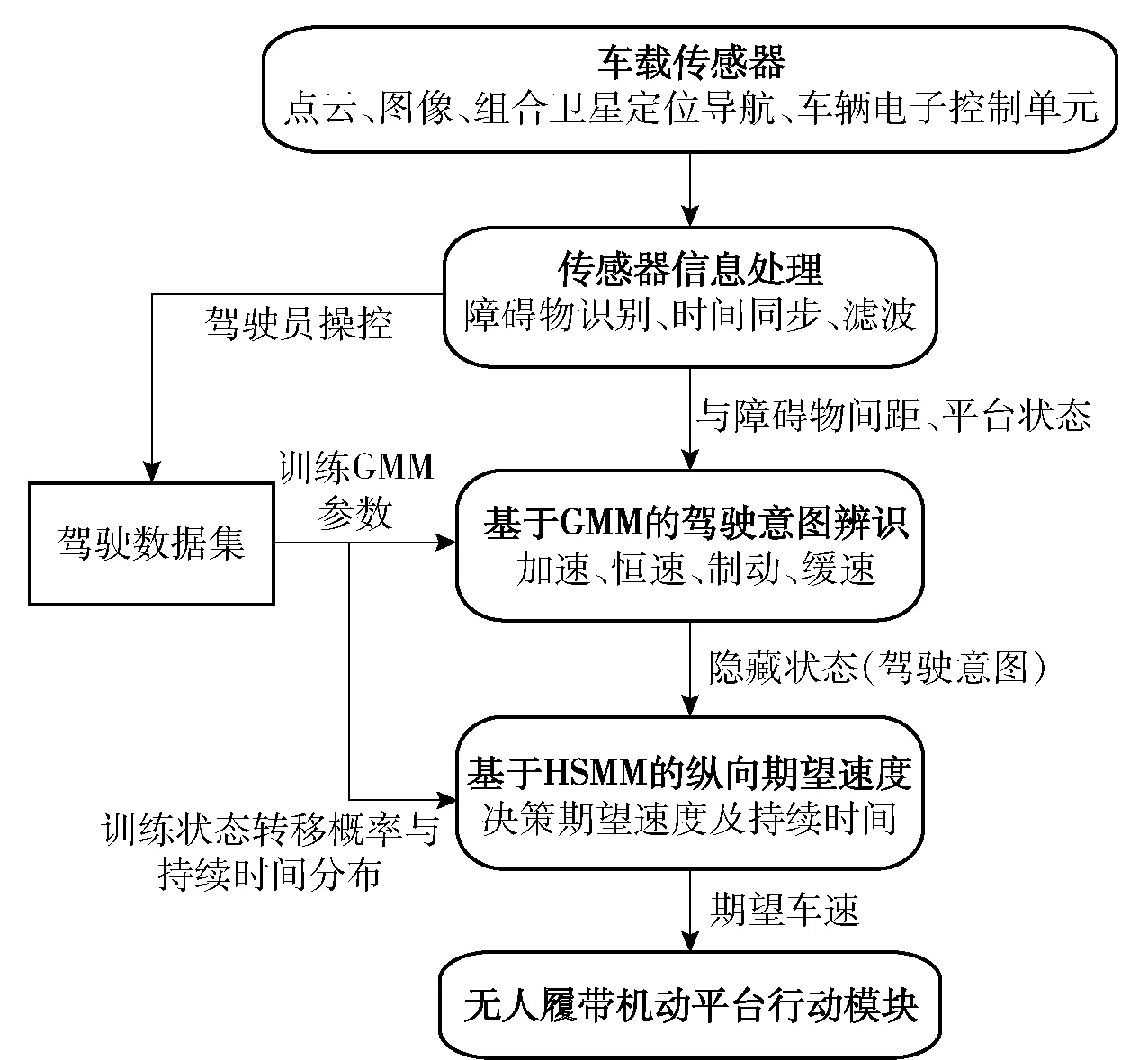
图3 电驱动无人履带平台类人纵向决策系统研究框图Fig.3 Research block diagram of human-like longitudinal decision-making system for electric unmanned tracked platform

2.1 基于GMM算法的驾驶意图辨识

在典型的有障碍物的直驶任务中，驾驶任务可以大致分解为如图3所示的4个部分，驾驶员的决策行为主要体现在根据当前车速、与障碍物间距产生适当的驾驶意图。为学习驾驶员的纵向行为意图变化过程，主要需要解决的问题有：

1)研究某一驾驶意图存在时的观测状态分布规律；

2)研究驾驶员在加速与制动过程中的期望速度变化量分布规律。

问题1主要反映了驾驶员在当前工况下产生某种驾驶意图的概率，问题2则期望量化驾驶员的加速与制动行为，因为在同一驾驶意图的不同阶段驾驶员可能具有不同的操控习惯。假设驾驶意图、期望速度变化量大小与当前车速、与障碍物间距、最大期望车速有关，因此建立GMM对不同驾驶意图、期望速度变化量分别进行聚类分析，得到其在全区间的连续概率密度函数。对整个区间内的常见观测区域进行统计概率描述，以GMM的最佳拟合个数作为行驶策略的划分依据。通过人工标注的方法标注出驾驶数据对应的驾驶意图。

假设在一次行驶过程中，时刻的观测向量=[,]，和分别为时刻平台的纵向车速(km/h)和与障碍物的相对距离(m)，长度为的连续观测向量构成了单次行驶的观测序列={,,…,||}，令该次行驶中的最大速度为，满足=max()，∈(0,||]。因此次行驶构成的数据集可以写为={,,…,}。为了简化GMM中高斯核与驾驶意图的对应关系，从经验上利用最大行驶速度将数据集划分为3个子集，分别满足∈(0 km/h,10 km/h]，∈(10 km/h, 20 km/h]和∈(20 km/h,30 km/h]。针对每一个观测序列子集，利用GMM对其在整个区间内的概率密度函数进行建模。多变量GMM如(1)式和(2)式所示：

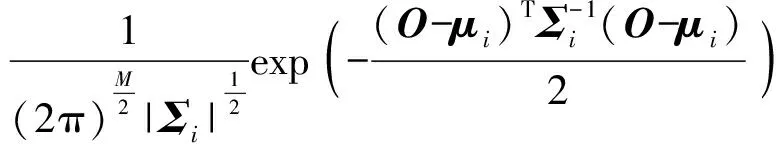
(1)

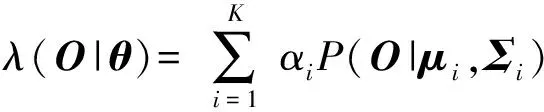
(2)

式中：(|,)为第个高斯分布；为观测向量的维度；和分别为第个高斯模型的均值矩阵和协方差矩阵；为第个高斯模型的先验概率值；(|)为观测序列的混合高斯模型；={,,…,}为混合高斯模型的参数集合，其中={,,}；为高斯模型的个数。

使用最大似然法估算GMM的参数，其最大似然函数如(3)式所示：

(3)

因为对于GMM无法使用求导方法得到使得(3)式最大的参数，所以需要利用一种迭代方法，即期望最大化(EM)算法求解。使用贝叶斯信息判据得到高斯模型的最佳数目，贝叶斯信息判据如(4)式所示：

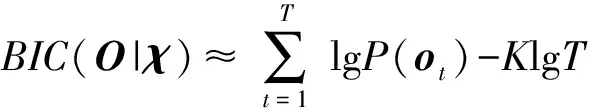
(4)

式中：BIC数值与模型拟合能力正相关；为所选GMM。实际上，一种驾驶意图可能对应多个高斯核，针对具有语义歧义的高斯核或聚类效果不满足要求的情况，通过调整值或在EM算法中设置高斯核均值和方差的初始值获得更好的学习结果。

在得到较好的聚类结果后，令()为时刻观测向量属于第个高斯模型的后验概率，计算方法如(5)式所示：

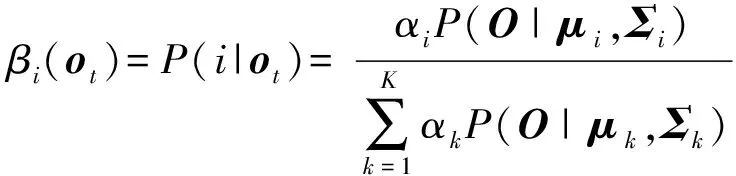
(5)

对于时刻观测状态向量的后验概率最高的高斯核求解方法为

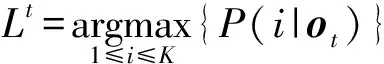
(6)

则认为该高斯核对应的驾驶意图即为时刻的驾驶意图。

2.2 基于GMM算法的操控行为聚类

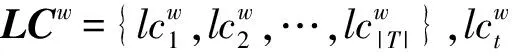
在操控行为聚类过程中，(|)是第种驾驶意图下操控行为观测序列的混合高斯模型，根据履带车辆驾驶员存在普通和谨慎两种驾驶风格，令高斯核个数=2，为混合高斯模型的参数集合。使用EM算法估计得到GMM中的参数，实现对驾驶员期望速度变化量的聚类。聚类结果决定了HSMM算法中显式状态集合中元素的大小。

2.3 基于HSMM算法的类人纵向决策建模

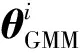
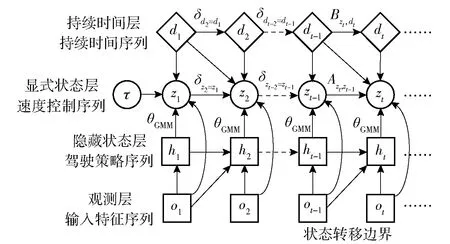
图4 基于GMM-HSMM的纵向速度规划系统Fig.4 Longitudinal speed planning system based on the GMM-HSMM

初始状态和持续时间的联合概率定义为(,)=()(|)，一个状态的初始概率用=()表示，而持续时间的概率用,=(|)表示，状态转移概率矩阵只作用于状态转移的边界。

在HSMM中，隐藏状态(,|-1,-1)的转移概率可以分解为

(,|-1,-1)=
(|-1,-1)(|-1,-1)

(7)

其中对应的定义为

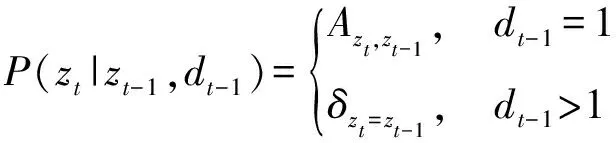
(8)

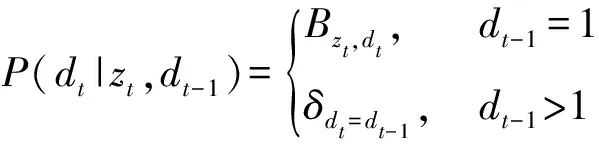
(9)

当=时，==1，否则==0。

状态持续时间参量是HSMM区别于传统HMM的关键点，参考人类行为建模研究，参数化分布模型更适用于状态持续时间建模。在本文中使用高斯分布拟合持续时间分布规律，对于持续时间的概率密度公式为

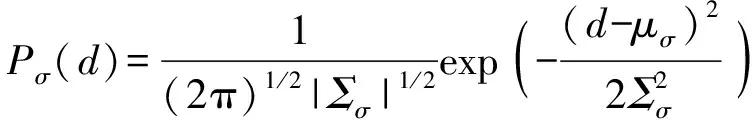
(10)

式中：和分别为高斯分布的方差和均值；为描述当前地面类型、期望车速与驾驶意图的参量。通过统计方法估计得到参数和，并将每种工况下的期望值视为最优值。

假设已知状态参量=，此时的观测向量概率服从多元高斯分布，为了便于实现这一点，观测向量在隐藏状态下的发射概率可以定义为

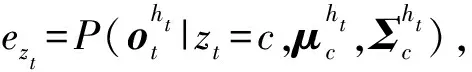
(11)

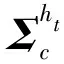
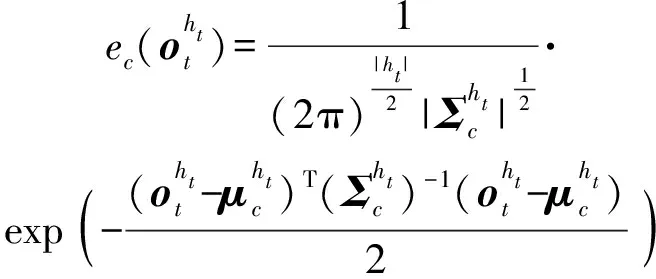
(12)

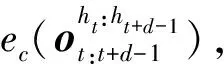
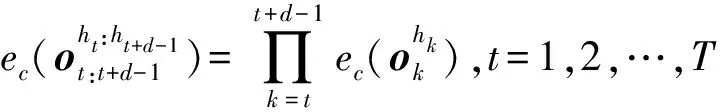
(13)

之后，HSMM可以由参数集={,,,}确定，给定训练驾驶数据集，使用迭代算法EM通过最大化似然对数lg(|)来获得最优参数集合。学习获得模型参数后，使用前向算法估计当前状态=，将前向递归变量定义为

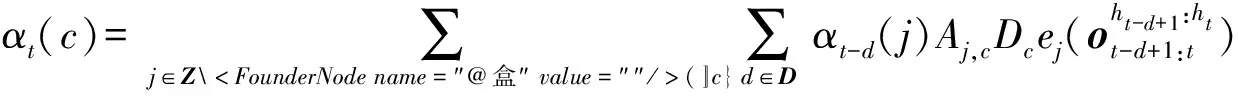
(14)

因此，基于前向算法的状态的估计值可以由(15)式计算而得：

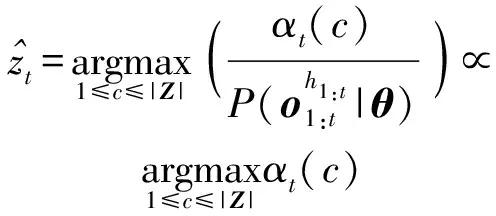
(15)

3 试验工况简介与数据处理

为了全面采集驾驶员在直驶接近障碍物过程中的驾驶数据，实车进行了共计40余次实车驾驶试验，试验中履带机动平台最大期望速度在5～30 km/h之间，对应初始距离在10～100 m范围内，车辆在行驶过程中加速、恒速行驶、制动和缓速接近4个阶段依次出现，且距离障碍物1 m时速度不高于2 km/h。共有3名驾驶员参与试验，包括2名初级驾驶员和1名持有特种车辆驾驶证的驾驶员，2名初级驾驶员在试验前在该平台上的驾驶时长均超过500 h。为了验证类人纵向决策模型的适应能力，在干燥土路和泥泞土路工况下进行了相同的试验。

试验履带平台的操控驾驶仪如图5所示，该驾驶仪为北京理工大学智能车研究所自主设计研制，驾驶员通过推动速度控制推杆向平台控制器下发期望车速，且期望车速为0～80的整数。在整车通信网络中，全局时间戳由组合导航模块发出，其余传感器和运算设备以此为基准进行时间校正从而实现同步存储。整车控制器和能量控制器负责底层执行单元并将数据发送到规划控制工控机，同时接收上层无人系统发送的控制指令，实现车辆控制。针对车辆行驶速度在30 km/h及以下的通信实时性问题，设计上层无人系统的数据处理周期、激光雷达和相机的采样周期为10 Hz，组合导航系统的数据发送周期为50 Hz，底层控制器CAN网络通信周期为100 Hz。

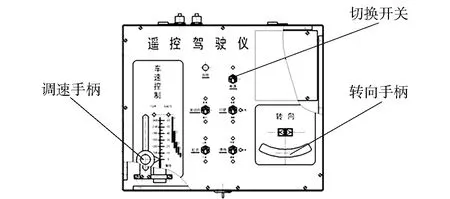
图5 电驱动履带平台遥控驾驶仪Fig.5 Remote driving controller of electric tracked platform

4 试验结果分析与模型验证

4.1 基于GMM的驾驶意图聚类结果分析

GMM对驾驶行的聚类分析结果主要包含驾驶意图在车辆速度、与障碍物间距下的联合分布概率，以及驾驶员在不同阶段下的操控行为量化。针对驾驶意图辨识，该部分分析了初始距离小于等于30 m下的加速过程以及全部的制动过程和接近过程。图6显示了当驾驶员分别处于加速、恒速行驶、制动和缓速接近意图时的车辆速度、与障碍物间距的概率密度分布。由此在已知平台观测状态的条件下，可以估计得到HSMM中的隐藏状态参量，从而得到在某种隐藏状态下基于统计结果的期望纵向速度的转移概率矩阵。由图6(a)可见，驾驶员在加速阶段最大期望速度和与障碍物间距直接相关，当距离大于20 m时更倾向于加速到15 km/h以上。在图6(b)的恒速行驶过程中，驾驶员恒速行驶距离随行驶速度而减少，即在高速时倾向于远距离制动。在图6(c)的制动过程中，驾驶员表现出3种制动策略，分别集中在低速近距离、宽速宽距离范围和低速远距离，其中宽速宽距离范围覆盖面积最大，反映了驾驶员在该速度范围内的制动习惯和履带平台本身的制动响应特性。图6(d)反映了驾驶员在缓速接近阶段将速度尽可能地控制在2～3 km/h左右，且行驶距离控制在3～4 m左右，普遍采取了较为保守的驾驶行为。

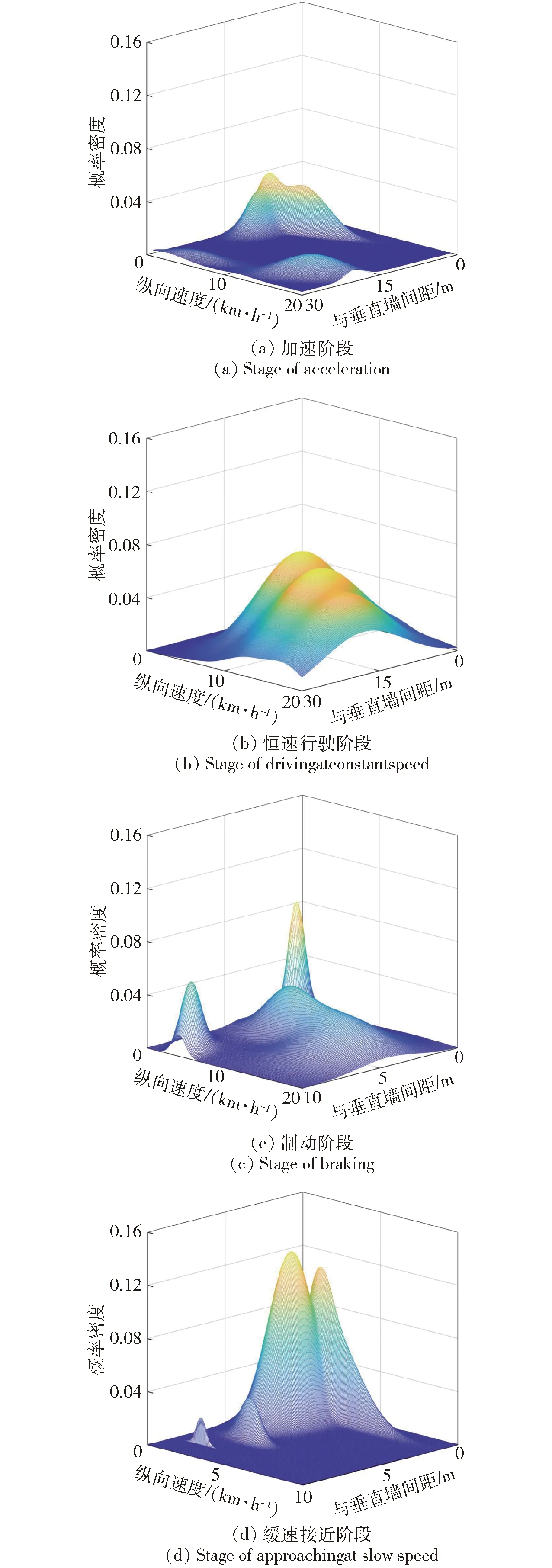
图6 基于GMM的驾驶意图聚类Fig.6 Cluster of driving intention based on GMM

4.2 基于GMM的驾驶操控量化聚类

在4个驾驶意图中，驾驶员通过操作遥控驾驶仪将离散的期望速度下发给车辆的执行机构。基于GMM方法对期望速度的阶跃信号差值进行聚类，获得驾驶员分别在加速、恒速接近、制动和缓速靠近意图下期望速度变化量的概率密度。由2.3节中对HSMM状态集合Z的定义可知，Z包括了5种操控方式，但在某一驾驶意图下并非所有操控方式均会出现，例如加速过程中几乎不会出现减速和换减速。并且在同一种意图中，同一种操控方式可能对应不同的控制变化量，例如在制动过程中驾驶员倾向于使用较大的减速变化量以保障平台安全性，然后通过较小的减速变化量缩短与障碍物之间的距离，从而提高行驶效率。

因此，使用GMM对驾驶员纵向操控行为进行聚类，并将聚类结果赋值给对应的HSMM显式状态集合Z。如图7所示：可以得到驾驶员在加速阶段的状态集合为{2 km/h,3 km/h,4 km/h,5 km/h,0 km/h}；得到驾驶员在恒速阶段的状态集合为{1 km/h,0 km/h,0 km/h,-1 km/h,0 km/h}；得到驾驶员在制动阶段的状态集合为{0 km/h, -2 km/h, -3 km/h,-4 km/h,-6 km/h}；得到驾驶员在缓速接近阶段的速度控制量为{0 km/h,1 km/h,0 km/h,-2 km/h,-1 km/h}，以及集合中元素对应的概率分布。驾驶员的控制行为将作为HSMM中显式状态参量，是量化驾驶员决策行为的重要依据。

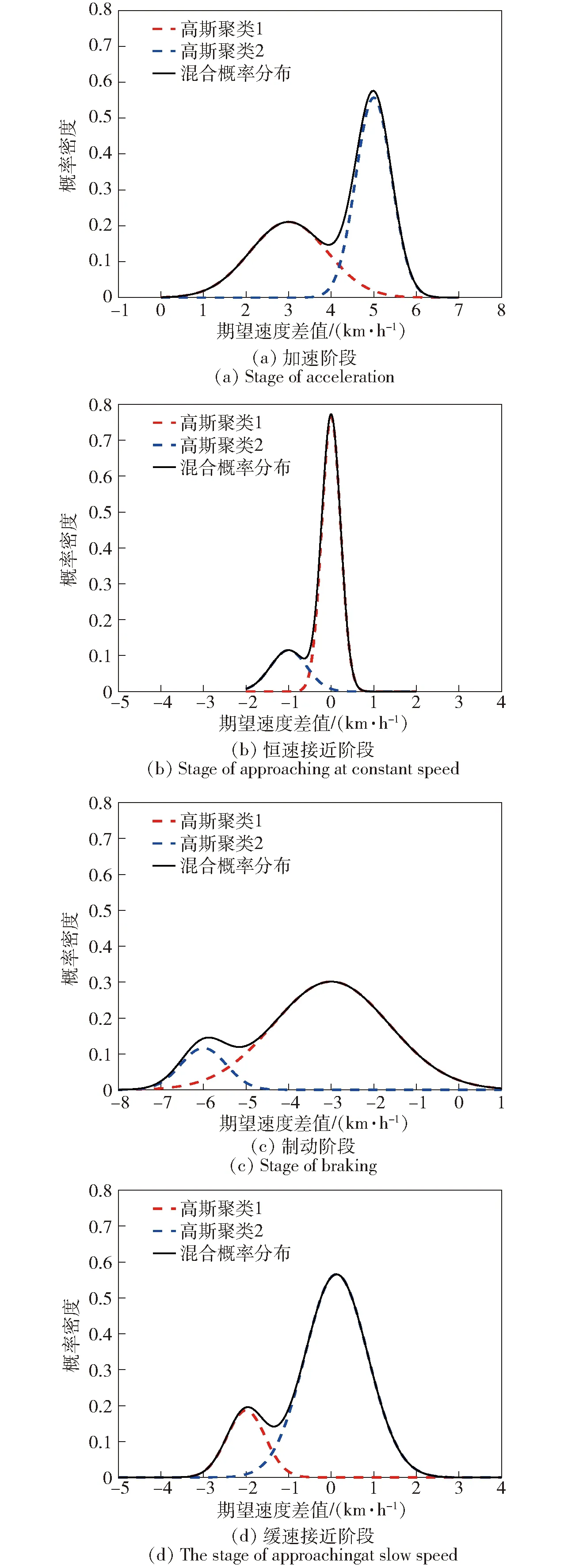
图7 基于GMM的驾驶员控制行为聚类Fig.7 Cluster of driver’s control behavior based on GMM

4.3 基于GMM-HSMM的类人纵向决策系统

在GMM-HSMM驾驶员模型中，通过GMM对观测向量进行驾驶意图辨识得到了HSMM中隐藏状态参量，以及驾驶员在全区间纵向速度控制量的分布规律，构成了HSMM中的显式状态层。为了估计HSMM中状态的持续时间，使用高斯分布对不同速度变化量下的持续时间进行拟合。

驾驶数据表明，熟练驾驶员在无法获得精确环境信息与车辆状态的情况下，依旧可以依靠对纵向加速度(推背感)的感知灵活、安全地驾驶电驱动履带机动平台。以图8中驾驶员在加速与制动过程中的操控结果、平台速度与加速度变化曲线为例，从虚线标记处可以直观发现，虽然驾驶员无法精确地知道平台是否已经达到期望速度，但是驾驶员可以通过感知加速度变化轨迹，在加速度接近零点时认为平台接近或达到期望速度，并习惯于在该状态时进行升速或降速操作。

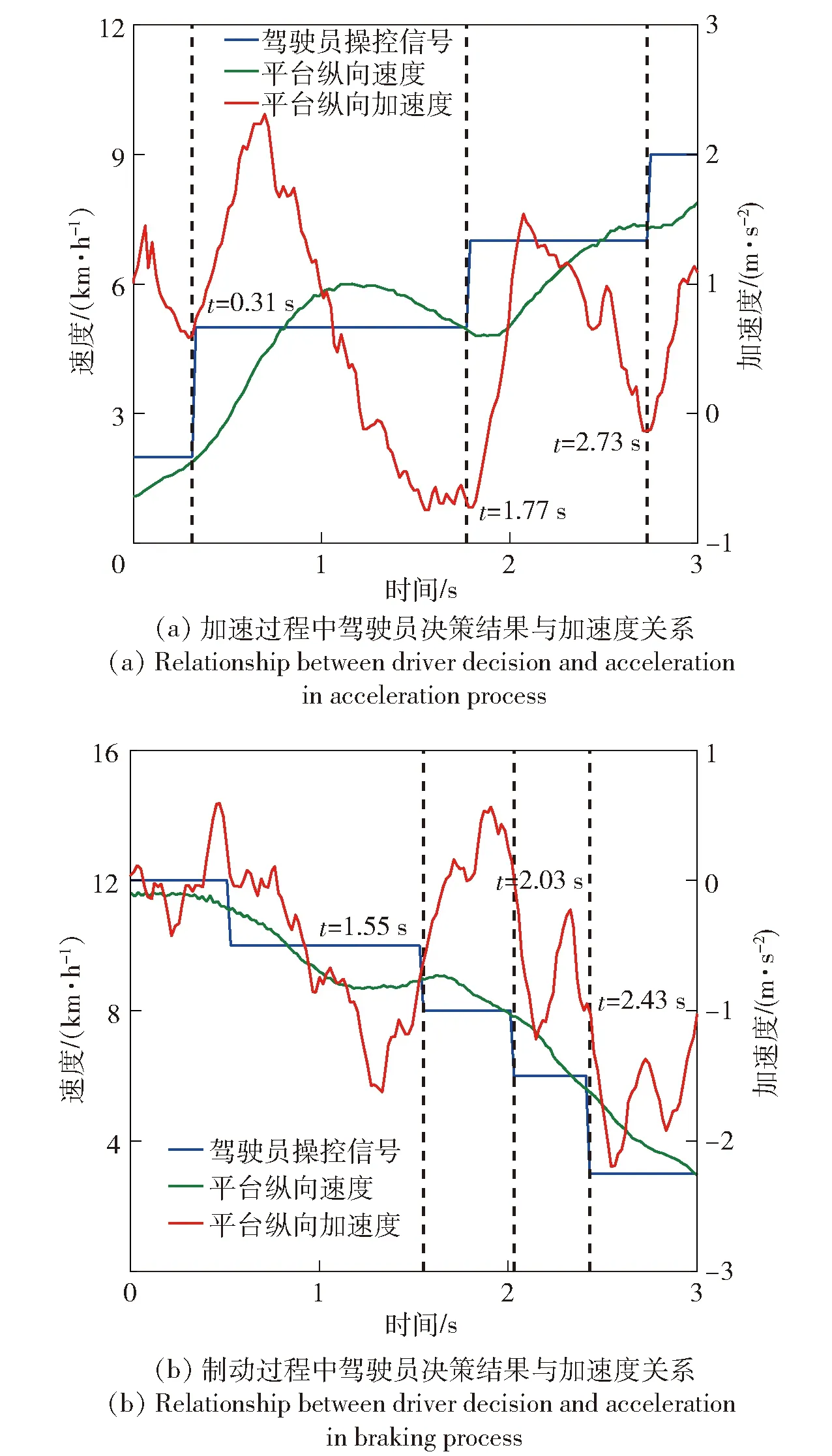
图8 平台加速度对驾驶员纵向决策影响Fig.8 Effect of platform acceleration on the driver’s longitudinal decision-making

因此，可以利用驾驶员基于加速度感知进行决策的这一驾驶特性，对驾驶员在某一期望速度上的持续时间进行参数化建模，从而将该特性引入到基于GMM-HSMM的类人纵向决策系统中。本文使用了高斯分布拟合驾驶员在不同地面条件下的决策持续时间特征，另一方面通过拟合驾驶员在不同地面条件下的决策持续时间，使得系统具备了不依靠精确参数而适应环境的能力，拟合结果如表2所示。在地面条件和速度增量均相同的情况下，初始速度越大，决策持续时间的均值和方差越低，反映了驾驶员在高速工况下对加速度变化的感知更敏锐。对于两种地面条件，由于履带平台在泥泞土路上的行驶阻力增大，平台加速性能降低，因此在泥泞土路工况下加速决策的持续时间的均值和方差都相对较大，而制动决策的持续时间的均值和方差则相对较小。对于制动过程，在泥泞土路上的持续时间只在初始速度较低的区间内缩短比较明显。拟合结果表明，通过驾驶员的体感特性可以有效地结合机动平台在多种工况下的动力特性与决策经验。该方法基于离线驾驶数据，利用结构简练的统计学模型避免了对精确地面参数的需求，具有增强学习型模型适应能力的巨大潜力。当加减速变化量等于0 km/h，即当前状态为恒速时，令恒速状态的持续时间均值等于上一状态持续时间的二分之一，方差与上一状态持续时间的方差相同。

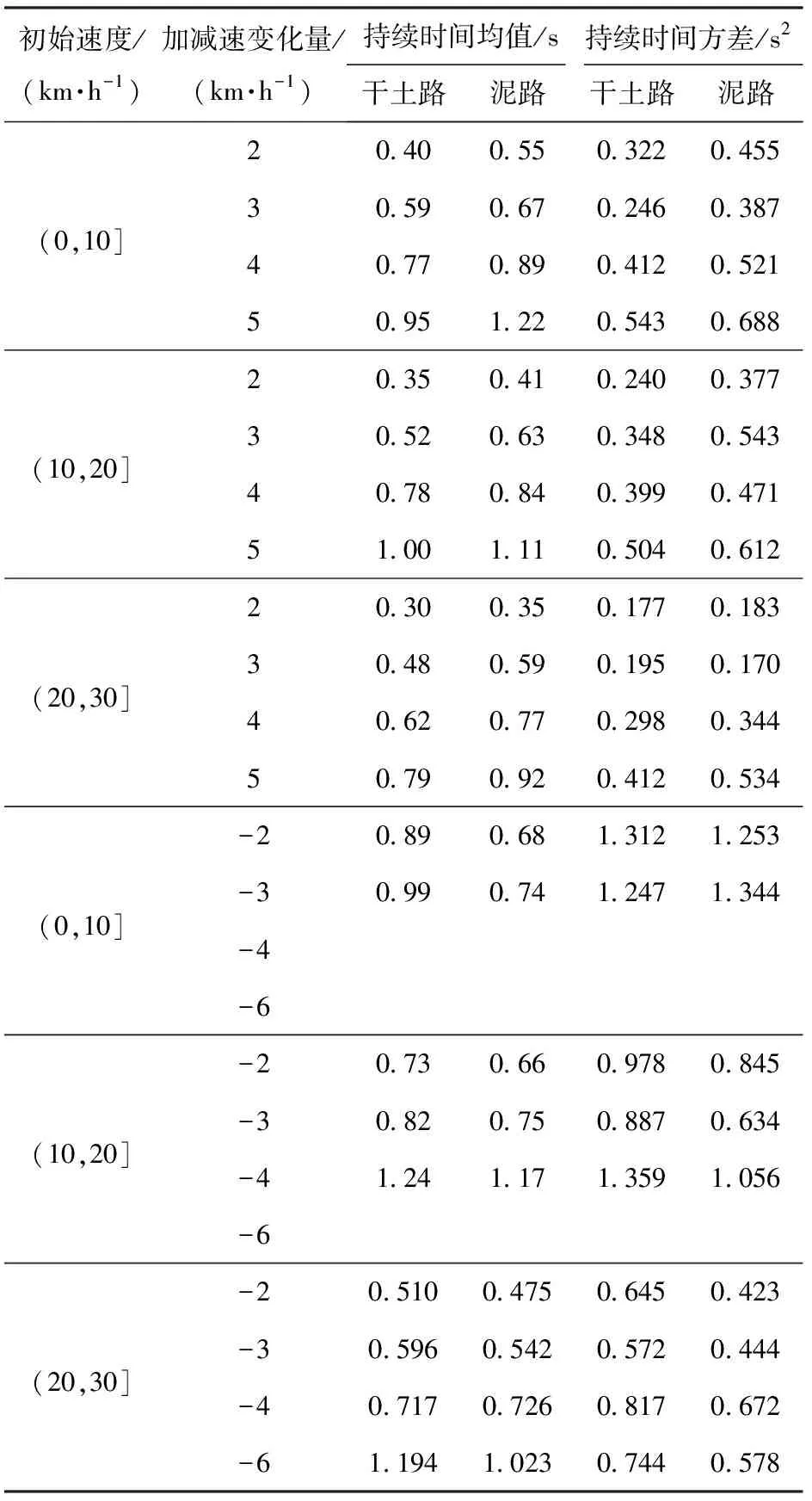
表2 持续时间高斯分布拟合结果

在学习得到GMM-HSMM类人纵向决策系统的参数集合后，将该方法应用于真实越野环境进行实车试验。因为越野环境的不确定性以及驾驶过程的随机性，很难完全模仿训练数据集中的驾驶员操控过程。因此，选取决策时的平台加速度值以及决策时的相对速度误差作为评价指标，以此评估系统的类人属性。图9举例展示了平台在两种地面条件且期望速度不大于20 km/h和30 km/h下的试验结果，可以直观地看出，通过控制状态持续时间大小，可以将状态转移时平台加速度的绝对值限制在一个较小范围内，同时兼顾决策发生时实际速度与期望速度的相对误差。表3显示了基于GMM-HSMM的类人纵向决策系统和熟练驾驶员在产生新的期望速度时加速度大小和相对速度误差，其中相对速度误差为当前车速与期望速度的差值占期望速度的比例。由表3可以看出，基于GMM-HSMM的驾驶员模型可以良好地模拟驾驶员的加速度感知驾驶特性，并不依靠精确地面参数而具备对环境的适应能力。

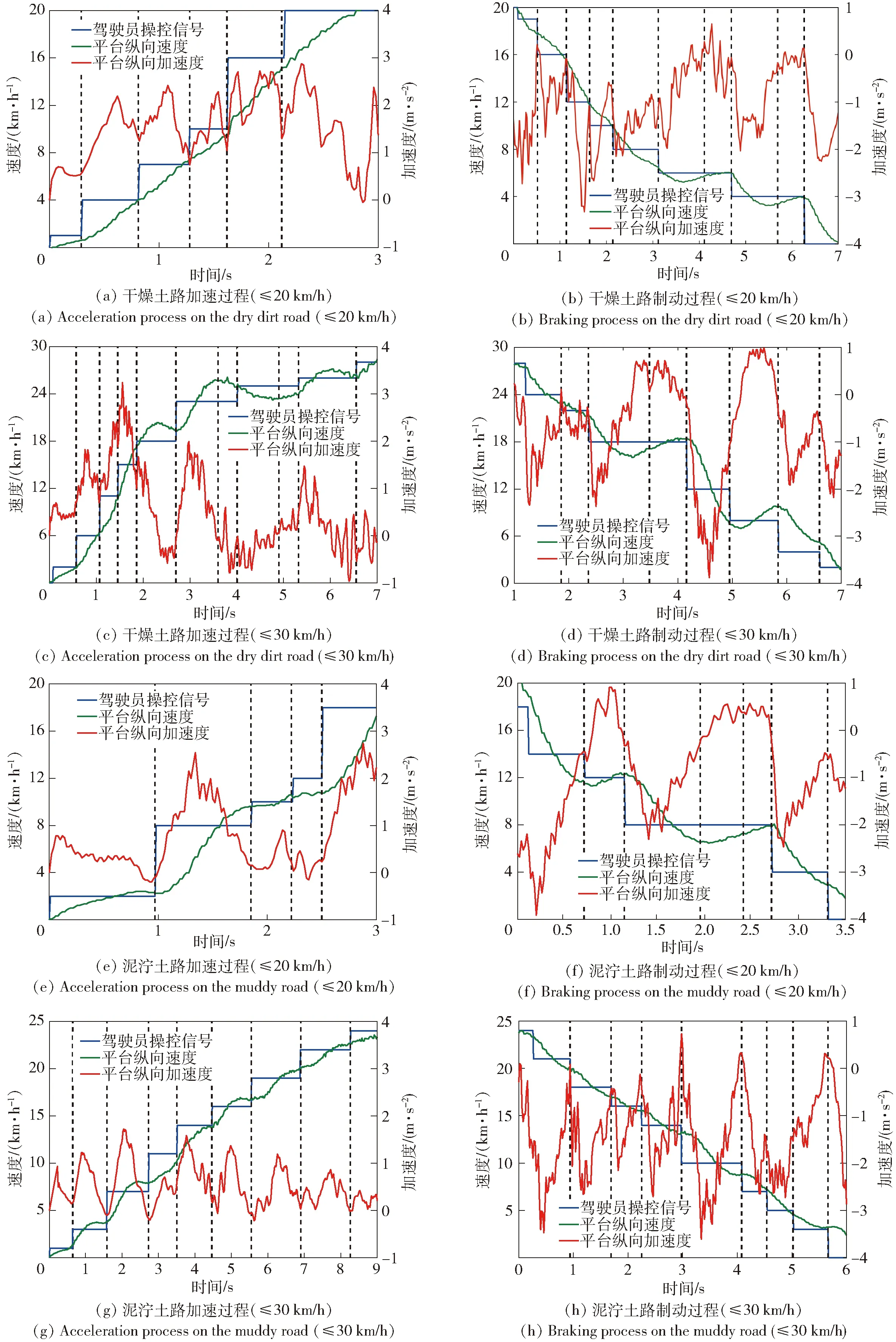
图9 基于GMM-HSMM的类人纵向决策系统在不同地面条件下的典型试验结果Fig.9 The typical experimental results of GMM-HSMM-based human-like longitudinal decision-making system with different road conditions

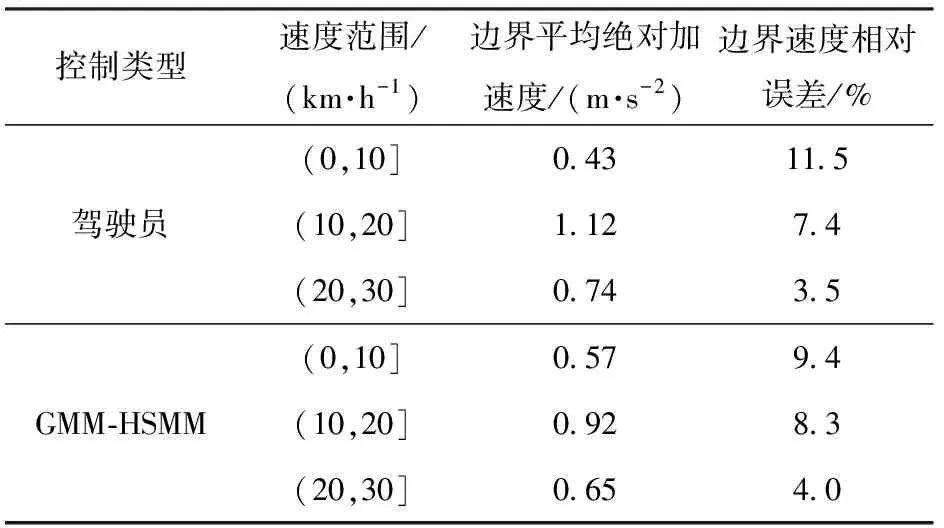
表3 基于GMM-HSMM的类人纵向决策系统评估

5 结论

本文基于搭建的双侧独立电驱动无人履带平台，通过采集包含驾驶员操控行为的真实驾驶数据，基于电驱动履带平台驾驶员对加速度的感知特性，在传统的HMM中引入了持续时间特征，并利用GMM模型学习了直驶过程中的驾驶意图与操控行为，实现了基于GMM-HSMM的类人纵向决策，并通过实车在不同地面条件下进行了验证。得出以下主要结论：

1)针对有障碍物的直驶的过程，基于GMM对驾驶员的意图和操控行为分别进行聚类，得到了驾驶意图和车速、与障碍物间距的统计学关系；聚类结果划分了驾驶员在不同阶段的加减速大小，为决策行为的量化提供了理论基础。

2)基于GMM-HSMM的类人纵向决策模型，克服了传统HMM模型对状态观测参量变化敏感的问题，还原了驾驶员的体感驾驶特性，从而将决策产生时的平台加速度限制在一个合理的范围内。

3)使用高斯分布拟合了持续时间特征，通过学习在不同地面条件下的驾驶数据，在不依靠精确地面参数的情况下使模型具备良好的适应能力。