基于车辆-行人轨迹预测的人车冲突预警策略研究*

施 雯 刘艳娟 赵 彬

（1.陕西青年职业学院财经系 西安 710068）（2.长安大学汽车学院 西安 710064）

1 引言

人-车冲突是一种典型的道路交通冲突场景，是驾驶员通过斑马线时需要避免的首要风险。相对于有信号灯控制的交叉口，无信号灯控制的交叉口无法从时间上对行人和机动车进行分离，机动车与车辆发生冲突的概率更大。为了降低行人伤亡事故的发生率或减轻事故的严重程度，越来越多的研究者开始致力于车载行人预警系统的研发［1～3］，该系统发展迅速，现已成为先进辅助驾驶系统的重要组成部分。

目前，车载行人预警系统主要借助车载传感器检测车辆前方行人［4～5］，一旦检测到有行人出现立即预警，忽略了上述行人在过街过程中的灵活性，降低了该系统的实际使用效果。另外，系统预警算法整体较为简单，尤其是阈值设置得较为宽松，导致预警信号出现频次过高，使得驾驶人对预警信号出现麻木心理和抵触心理，对系统的推广使用造成了一定的影响。故本文提出利用车载传感器检测到车辆前方行人后，对其未来几秒内位置进行预测，并结合车辆未来的行驶策略判断行人和车辆是否存在碰撞冲突，根据是否存在人车冲突进行预警，这对于提高车载行人预警系统的实用性具有重要的意义和研究价值。

2 相关工作

近些年来，基于数据驱动的算法在轨迹预测模型中的应用较为广泛，主要有社会力模型、动态贝叶斯网络模型、隐马尔可夫模型、基于人工智能的深度学习算法等［6～8］。其中，隐马尔可夫模型（Hidden Markov Model，HMM）是一种统计模型，它被用来描述一个含有隐含未知参数的马尔可夫过程，马尔可夫过程是研究离散事件动态系统状态空间的重要方法［9］，目前，在行人轨迹预测方面的应用也较为广泛。毛莺池等对基于马尔可夫链的轨迹预测算法的路径补全算法进行重新定义，从而缩短了查询时间，进一步提高预测准确度［10］。Wesley Mathew 等提出对车辆的历史运动轨迹特征进行聚类，每类轨迹训练一个隐马尔可夫模型［11］。Ye 等提出了一种基于双隐状态隐马尔可夫模型的轨迹预测算法［12］。Qiao 等基于密度的轨迹划分算法将运动轨迹分成一系列的段，作为隐马尔可夫模型的隐状态，然后利用维特比算法寻找最大似然的隐状态链，通过正向算法计算下一个时刻目标的位置［13］。隐马尔可夫模型对比社会力模型具有较高的预测精度，同时，相比于深度学习等人工智能算法，具有计算简便、易于理解等优点。

本文着重研究车辆和行人在交互过程中的冲突预测问题，提出了一种基于隐马尔可夫模型的车辆-行人轨迹预测模型，将Viterbi 算法与状态转移概率矩阵和发散概率矩阵相结合，通过已知的目标轨迹数据来预测车辆和行人的未来轨迹数据，提出一种车辆-行人冲突判断规则，用于判断车辆和行人在未来时刻是否会发生交通冲突。

3 试验与数据获取

本文将试验地点选择在西安市某无信号灯控制路口，如图1 所示，将车载激光雷达和微型摄像装置安装在交叉口路侧，其中，车载激光雷达用于采集车辆和行人的运动特征，微型摄像装置用于采集车辆和行人的行为特征，通过试验，共获得到910 组车辆和行人过街数据，每组数据包括行人过街类型、车辆类型、车辆驾驶员是否主动让行、车辆和行人在初始状态时与路缘的距离、各时刻车辆-行人的速度值及相对应的位置(x,y)坐标值。

图1 试验示意及现场对照图

如图2 所示，我们将行人越过路缘或者踏上路缘的时刻定义为初始时刻t1，以初始时刻t1作为该条数据时间序列的起始点，记录穿越斑马线的行人的速度和坐标、车辆的速度和坐标数据。

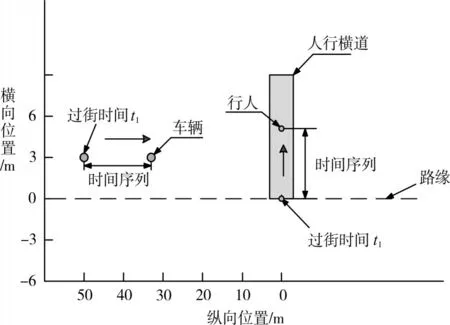
图2 车辆与行人的运动关系

车辆和行人在t时刻与t+1 时刻之间的运动距离为

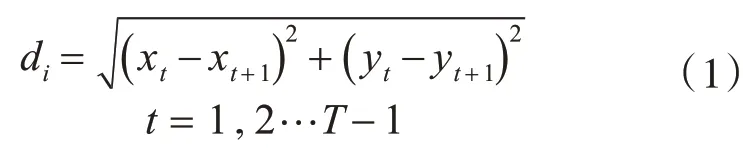
行人在t时刻的运动角度为

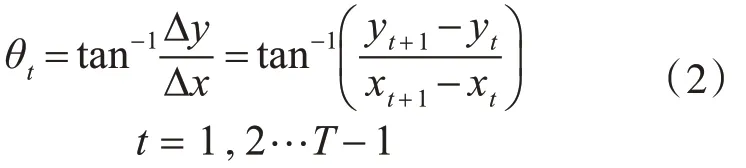
在上式中，xt表示目标在t时刻的横坐标，yt表示目标在t时刻的纵坐标，T表示坐标点取样时刻。

4 基于隐马尔可夫模型的轨迹预测方法

本文将行人轨迹预测分为距离预测和方向预测。车辆在接近斑马线时行驶方向基本不会改变，只对其进行纵向距离预测。

4.1 基于Baum-Welch算法的参数离散训练

本文将目标的速度v定义为HMM 的隐状态变量I，目标在相邻两个取样点之间的距离d或者方向θ定义为观测状态变量O，如图3所示。本文所选每组人-车冲突数据时间长度均为1.92s，规定每0.167s取一组行人和车辆的位置坐标，1.92s内可得到12个坐标值，令时间序列T={1 ,2,…11} 。

图3 隐马尔可夫模型原理图

HMM 中的隐状态集合和观测状态集合要求为正整数集合，故需要对采集到的910 组数据进行离散化。如表1、2 所示，离散化处理后的行人距离数据集对应的观测状态集合为V1={1 ,2,…11} ，行人速度对应的隐状态集合为Q1={1 ,2,…19} 。将行人运动方向划分为8 个离散值，观测状态集合V2={1 ,2,…8} ，对隐状态的含义不进行具体定义。同样，如表3、4 所示，对车辆速度和距离数据进行离散化，隐状态集合为Q3={1 ,2,…25} ，观测状态集合V3={1 ,2,…21} 。

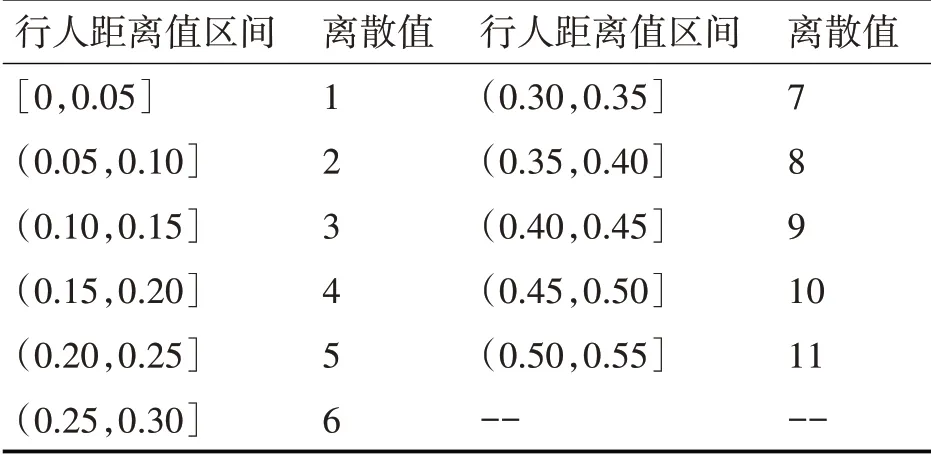
表1 行人距离值区间对应离散值

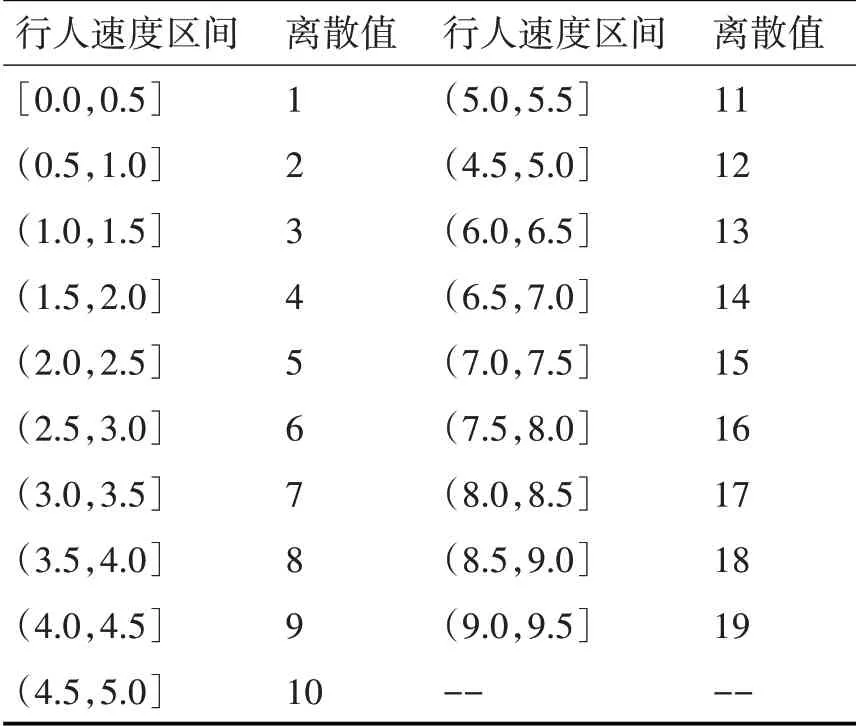
表2 行人速度值区间对应离散值

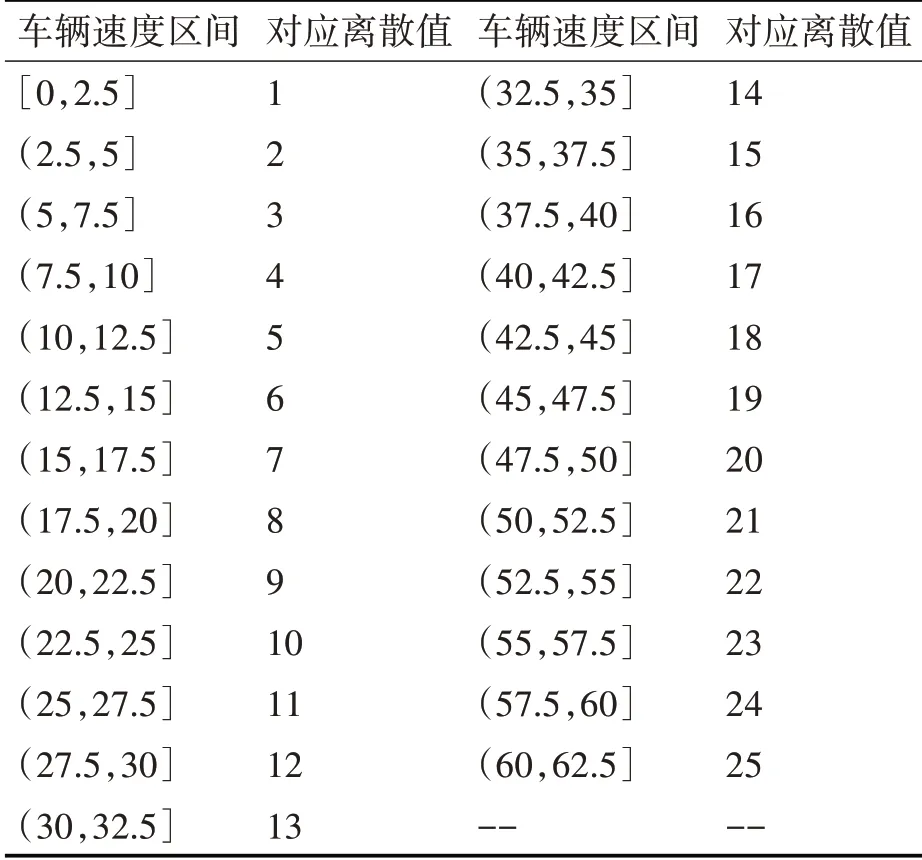
表3 车辆运行速度区间对应的离散值

表4 车辆运行距离区间对应的离散值

本文需要通过训练获得的HMM主要参数包括初始状态概率分布矩阵π，状态转移概率矩阵A发散概率矩阵B，为λ=(A,B,π) 。训练模型参数属于HMM 中的学习问题，即对于给定的观察状态序列O={o1,o2,…,oT}，求解模型参数λ=( )A,B,π ，使得在该模型下观测状态序列的概率P( )O|λ最大。

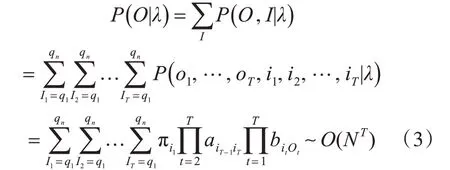
P(O|λ)计算的时间复杂度为O(NT)，其中，N是隐状态集合的元素数目，T为状态序列长度。为了缩短训练时间，采用非监督学习方法来进行参数估计。假设给定训练集包含S个长度为T 的观测序列，而没有应对的状态序列(O1,O2,…,OT)。我们将观测序列数据看作观测数据O，状态序列数据看作不可观测的隐数据I，那么隐马尔可夫模型实际上是一个含有隐变量的概率模型：

参数学习可以由Baum-Welch 算法实现，该算法属于EM算法的一种，其主要参数计算公式如下：

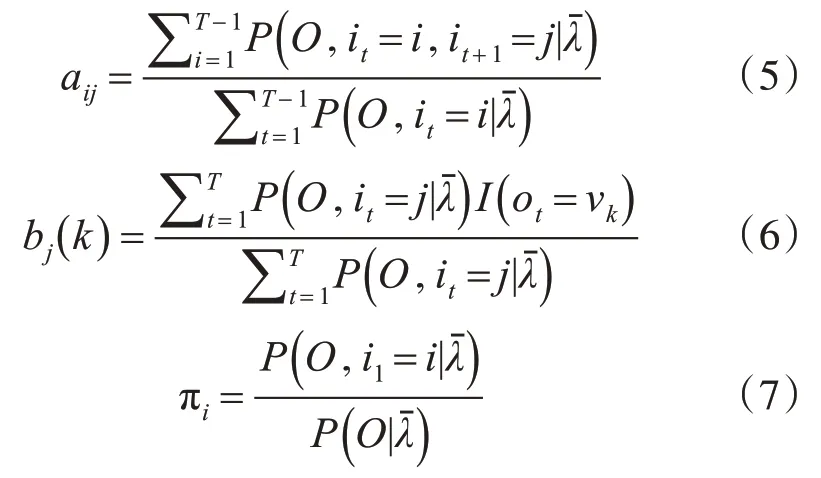
抽取70%的车辆-行人轨迹数据作为训练样本，与自定义的初始参数作为离散化隐马尔可夫模型参数训练算法的输入，对模型进行迭代更新，得到的参数：

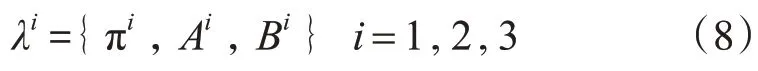
其中πi为初始状态概率矩阵、Ai为状态转移概率矩阵、Bi发散概率矩阵，λ1为行人距离预测模型参数，λ2为行人方向预测模型参数，λ3为车辆距离预测模型参数。

4.2 基于维特比算法（Viterbi）的轨迹预测

本文将Viterbi 算法与状态转移概率矩阵和发散概率矩阵相结合，利用前1.44s 的目标轨迹数据预测未来0.48s内的轨迹数据。

已知轨迹预测模型的参数λi=( πi,Ai,Bi)情况下，假设观测状态序列为O={o1,o2,…,otobs}，使用Viterbi 算法预测得到该观测序列对应的隐状态序列I={i1,i2,…,itobs}。

Viterbi需要引入两个变量δ和ψ，δt(i)表示在时刻t隐状态为qi的所有单个路径（i1,i2,…,it）中概率最大值，其表达式为

ψt(i)表示在时刻t，隐状态为qi的所有单个路径（i1,i2,…,it）中概率最大的路径所对应的第i-1个节点，其表达式为

模型输入为λ=(A,B,π )和观测状态序列O={o1,o2,…,oT}，输 出 为 最 优 路 径I*=(i1*,i2*,…,iT*)，计算过程为

1）初始化：

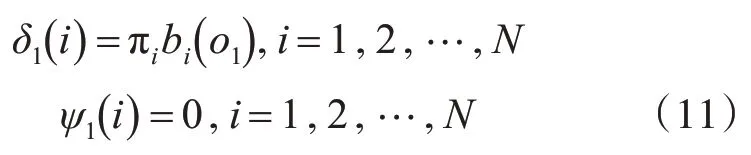
2）递推：对t=2，3，…，T

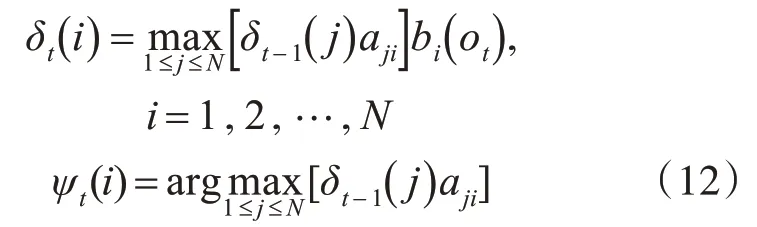
3）终止：

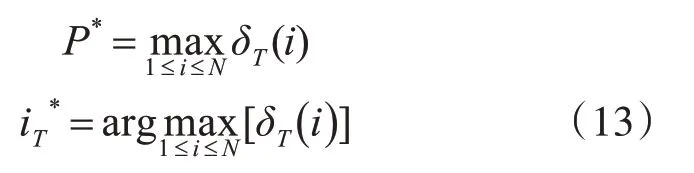
4）最优路径回溯：对t=T-1，T-2，…，1

5）求得最优路径I*=(i1*,i2*,…,iT*)。

通过上述Viterbi 算法求出观测序列O={o1,o2,…,o8}对应的最优隐状态序列I={i1,i2,…,i8} ，即通过前8 个取样点的距离值求出其对应的速度值，i8为第8 个取样点的隐状态值，然后通过状态转移概率矩阵A计算出第9 个取样点最有可能的隐状态值i9，再结合隐状态值i9对应的发散概率矩阵B计算得到每一个观测状态离散值的概率分布。为了避免状态转移概率矩阵A的“惯性”，本文采取将所有隐状态对应的观测离散值分布概率相加得到每一个观测离散值的概率。按照上述过程，完成第9、10、11 个取样点距离和方向值的预测，为了反映预测结果的可靠性，将第9 个取样点的距离和方向预测结果与真实值之间的误差绘制成折线图，如图4所示。

图4 第9取样点模型预测误差

可以看出，本文提出的基于HMM 的行人运动距离预测模型准确度较高，第9 个取样点行人的运动距离预测误差基本小于0.05m，只有个别数据误差达到0.2m 左右。第9 个取样点车辆距离的预测误差大致在0.1m 左右，表现出较好的预测精度。但是该模型在行人运动方向预测方面表现较差，误差较小的基本分布在40°左右，预测结果误差较大的达到100°以上，通过对误差较大的数据样本的分析，容易发现误差的存在主要是由于行人过街犹豫，产生的等待过街行为，对直接过街和等待过街行为分开讨论，从表5 中可以看出，不同过街类型的行人运动方向预测误差表现出了差异性，对于直接过街类型的行人，其预测的三个方向误差均小于20°，而等待过街类型的预测方向误差基本在50°左右。

表5 各模型预测平均误差表

5 人-车冲突判定规则与验证

通过上文的分析，本文提出的轨迹预测模型可根据现有时间长度为1.98s 的轨迹数据计算未来0.48s 的轨迹数据，基于此，可以判断未来可能发生的人车冲突。本文排除车辆主动让行的情况，当车辆在未来0.48s 的制动减速度大于3.0 m s2或行人在未来0.48s 内过街速度显著上升，则认为当前存在人车冲突［14～15］，根据以上规则对试验得到的910组数据进行冲突标签设定，共得到54 组真实的冲突数据。

分析行人过街模式与车辆到达斑马线时间（TTZ）相关性时，发现行人原地徘徊时对应的车辆到达斑马线时间均值为3.16s，故本文取TTZ为3.0s作为判断二者是否存在潜在冲突的时间阈值。

如图5 所示为一组真实冲突样本，当车辆在接近人行横道过程中，预警系统在TTZ=3s 时判断行人轨迹状态，计算在未来0.48s 内行人预测的横向位置，若预测行人横向位置在红色区域内，则可以判定存在潜在人车冲突的可能性。

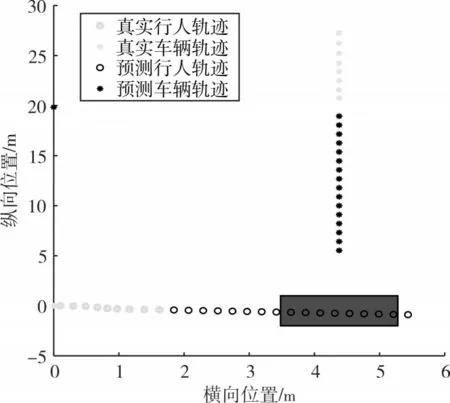
图5 冲突情况

按照以上冲突判定方法，基于目标轨迹预测模型，计算910 组车辆和行人在未来0.48s 的轨迹数据，然后将前1.44s 的真实轨迹与预测得到的未来0.48s 数据代入冲突判别规则中，判别车辆和行人在未来0.48s 内是否存在冲突的可能性，最后将真实冲突和预测冲突的样本进行对比，计算预测得到的冲突在真实冲突中所占的比例，结果如表6 所示，当冲突阈值TTZ 设置为3s 时，模型的冲突识别率最高，准确度为79.6%。

表6 冲突预测结果

6 结语

本文提出一种基于隐马尔可夫模型的轨迹预测模型，该模型对行人距离和车辆距离的预测准确度较高，对于直接过街类型的行人运动方向预测准确度较高。建立人车冲突判定规则，将TTZ=3s作为判断车辆与行人是否存在潜在冲突的阈值，冲突的识别准确率为79.6%，能够有效提高车载行人预警系统的预警准确度。虽然本文提出的模型能较准确地预测人车冲突，但仍存在不足，本文没有考虑目的地对于行人运动的牵引效果，另外从主观感受建立冲突的设定也不严谨，这些方面在以后的研究中都有待提高。