自适应骨干花授粉算法*

段艳明 肖辉辉 谭黔林 赵翠芹

（河池学院大数据与计算机学院 河池 546300）

1 引言

随着科学技术的日新月异，云计算、人工智能、5G、传感网、大数据和脑科学等众多新技术新理论和社会经济的高速发展，许多科学研究和实际工程问题日益复杂化，其各领域中所涉及的各类复杂优化问题的处理，越发成为社会各行各业迫切需要解决的问题，这些问题的求解对优化技术提出了更高的要求，即求解精度要高，计算速度要快，稳定性要好，而传统的优化方法（如Lagrange 乘数法及单纯形法等）在解决这些复杂优化问题时存在计算精度不高且耗时过长等不足。为了解决这些求解优化问题存在的瓶颈，人类需要寻求新的方法和途径。受自然界进化规律和生物群体智能行为的启发，一系列智能算法不断被提出，并且由于这些元启发式智能算法具有不需要传统优化方法所需要的连续、可微等限制条件的优点，这为解决复杂的优化问题提供了一种新途径和新思路。

依据显花植物繁殖机理，Yang 设计了一种名为花授粉算法（Flower Pollination Algorithm，FPA）的智能优化算法［1］，由于该算法实现过程简单且具有较好的全局探索和局部开采平衡能力等优点，使其在大量优化领域取得了成功应用。当前，该算法已被成功应用到企业投资分配［2］、医学［3］、能源［4～7］、传感网［8］等领域。然而该算法与其他智能算法一样，也存在一些不足，如算法演化后期计算速度慢、容易早熟，寻优精度不高，鲁棒性差等缺陷，导致其在解决大量复杂优化问题时获得的结果不尽人意。为了克服这些算法存在上述的不足，提高其收敛能力，当前众多学者依据各种智能算法的特征和优缺点，运用了诸多的策略和方法对其进行了改进，构建了许多优化能力更强的新算法模型，使得大量的工程优化问题得到更好的解决。因此，许多学者也对FPA 算法进行了深入改进研究，如Singh等［9］利用函数适应度值对转换概率p 进行动态调整，并取得了较好的效果；Tawhid 等［10］利用鲸鱼优化算法的搜索猎物策略和攻击猎物方法替换了FPA 算法的全局搜索策略，构建了一种新的混合算法WOFPA（Whale Optimization Algorithm and Flower Pollination Algorithm），其性能与对比算法相比，得到了一定程度的提升，但该算法增加了较多的参数，降低了算法的灵活性，并只在低维上验证了其性能的优越性，没有在高维得到验证，使其缺少了说服力；Gálvez等［11］为了改进标准FPA 算法在优化多模态问题时，仅依靠其莱维飞行策略和授粉稳定性机制无法找到多个最优解的缺点，提出一种多模态花授粉算法MFPA（Multimodal Flower Pollination Algorithm），其思想是在基本花授粉的基础上加入记忆机制识别潜在的全局和局部最优解，引入一种新的选择机制确保解的多样性，融入净化记忆处理方法循环消除重复的解，通过对14 个标准测试函数的优化，验证了其有效性，且性能优于对比算法；El-Shahat 等［12］提出了一种改进的花授粉算法，该算法利用惩罚函数对每个解进行评估，对解中的不可行解运用FRIO（Flower Repair and Improve Operator）进行处理，经过全局搜索或者局部搜索后，产生的新解再与全局最优解进行交叉操作，然后采用S函数对改进算法进行离散化，并对多维背包问题进行求解，其优化性能要强于对比算法。

从上述可知，当前的改进方法对FPA算法的优化性能具有一定的提升，但这些改进的FPA算法的优化能力还有较大的提升空间，且一些改进策略降低了算法的灵活性和增加了算法的复杂性。为此，本文提出了一种自适应骨干花授粉算法（Adaptive Bare Bones Flower Pollination Algorithm，ABFPA），算法把骨干思想利用到FPA算法的局部搜索部分，通过自适应搜索中心的高斯变异对花朵个体进行位置更新，在此基础上进一步利用指数变异进行位置优化；同时，在保留基本FPA 算法的个体信息共享思想的基础上增加信息共享的个体数量，更大程度上进行个体的有效信息交换。实验结果表明ABFPA 算法简单且高效，寻优效果好，收敛速度快，鲁棒性好，与现有经典的改进FPA算法相比，亦显示出良好的竞争力。

2 FPA算法的优化原理与优劣

FPA 算法是依据显花植物繁殖机理而设计的一种优秀的智能优化算法。从其仿生原理可知，其全局搜索策略是模拟植物繁殖的异花授粉过程，而植物异花传粉过程具有莱维飞行特征，这使FPA算法具有良好的探索能力，FPA 算法的局部搜索机制是源于植物繁殖的自花授粉过程。同时，学者Yang 通过参数p 较好地处理了算法的探索和开采的平衡问题。

然而，从算法的局部搜索方程可知，其局部搜索是通过两个随机的个体进行信息共享，增强了算法的种群多样性，但单纯地通过两个随机个体的信息共享来实现局部搜索，缺少个体位置更新的引导性，信息共享程度低，因此，FPA算法的局部优化能力较弱，制约着算法的优化性能。

3 自适应骨干花授粉算法

针对FPA 算法的局部搜索方程存在的不足和骨干思想的优点，本文提出了把骨干思想融入到FPA 算法的局部搜索策略中，运用高斯变异的随机分布策略来保持种群的多样性，同时对高斯分布的搜索中心进行自适应调整，达到个体根据算法的进化程度来进行高斯变异；高斯变异增强了种群多样性，但分散的个体也导致局部搜索速度和精度降低，并易脱离全局最优位置，为此在高斯变异的基础上进一步进行指数变异，使个体即保持多样性又较集中在最优区域，从而提高算法的局部搜索速度和精度；另外，通过0.5 的概率进行二分交叉，对FPA 算法的局部搜索方程再增加一个随机个体，通过两组个体的差分矢量来扰动个体的进化，进而更大程度上增强了种群的多样性和开采能力。

3.1 自适应搜索中心高斯变异

依据PSO算法的仿生原理可知，种群在演化过程中每个解都要利用进化中的两个最优个体（全局和个体）进行更新，文献［13］提出每个种群个体都收敛于其自身的历史最优值和全局最优值的加权平均值，与算法的参数设置关系不大。在此基础上，2003年Kenedy等提出BBPSO算法，该算法中的高斯分布是以pbest和gbest为两点的固定模式进行搜索，而错过了所有有效区域或尽可能多的区域，忽略了种群中的普通个体，未能利用到更多个体所携带的有用信息，限制了种群的多样性和算法的优化性能，导致算法易陷入局部极值，这是现有的骨干算法存在的主要问题。另外，由于事先并不知道pbest和gbest的相对位置，当算法陷入局部最优时，依靠随机产生的变异个体来跳出局部极值具有一定的难度。针对以上分析，本文把骨干思想引入FPA 算法的同时对高斯变异的搜索中心均值μ和方差δ进行自适应调整，增强花朵个体的多样性。

首先，确定花朵i在d维进行更新时的榜样花朵xm。利用式（1）计算变量b，随机产生一个数a∈(0,1)，若a＞b，xm为当前种群中的一个随机花朵，否则，xm为全局最优花朵，如式（2）所示：

其中，xi是随机花朵个体，xbest是全局最优花朵个体。

接着，确定高斯分布的均值μ。以最小化问题为例，按照式（3）～（6）计算μ的取值范围[μmin,μmax]，按式（7）得到高斯分布的均值μ：

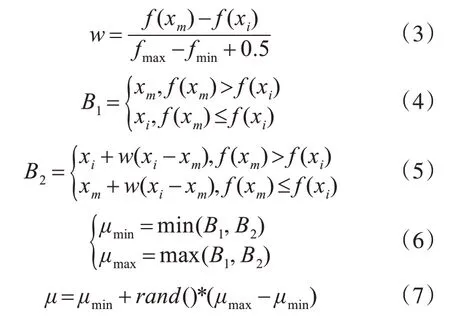
式（3）中的fmax和fmin分别为当前种群的最大值和最优值，其扩展因子w的范围为（-1，1）。当花朵i优于榜样花朵m时，有f(xm)＞f(xi)，w为正值，μ值向着当前花朵i的方向扩展；当花朵i劣于榜样花朵m时，有f(xm)＜f(xi)，w为负值，μ值向着榜样花朵m的方向扩展。在算法迭代初期，种群较为分散，花朵i远离榜样花朵m，则xi和xm相差较大，f(xm)和f(xi)的差异也较大，扩展因子 ||w也较大，进而B2值也较大，最终使得μ的取值范围中较多地为较优花朵的区域，更多地关注了较优花朵；随着迭代的进行，种群趋于集中，xi和xm的差异逐渐减小，f(xm)和f(xi)的差异也逐渐减小，扩展因子 ||w较小，μ的取值范围也逐渐缩小。因此，自适应高斯变异的方差μ满足算法前期的勘探能力和后期的开采能力的性能要求。

然后，确定高斯分布的方差δ。若花朵i即为上一代的最优个体，则根据式（8）计算方差δ，否则，按式（9）计算方差δ：

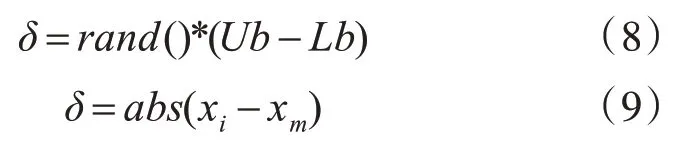
其中，Ub为函数的取值范围的上限，Lb为函数的取值范围的下限，xi为当前花朵位置。

最后，通过式（10）得到高斯分布的花朵位置：

3.2 指数变异

通过高斯分布得到随机的花朵个体，很大程度上增大了种群中每个个体之间的差异性，从而达到改善算法的局部搜索能力，但也在某种程度上降低了算法的局部搜索速度和精度。因此，本文在高斯分布的基础上再采用指数变异，使高斯分布的随机个体进一步向最优位置靠拢。指数公式为

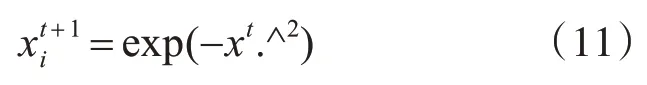
3.3 个体信息共享

标准FPA 算法的局部授粉（优化）部分是单纯通过随机的两个个体之间的矢量差来进行信息共享，在本文算法中除了通过高斯变异和指数变异来改进局部优化部分外，还遵循了标准FPA算法的局部授粉（优化）思想，依然利用了个体信息的共享，只不过在此基础上，通过0.5的概率进行二分叉，当产生的随机数小于0.5 时进行高斯变异和指数变异，否则把进行信息共享的个体增加到3个，通过1组1个随机个体与当前个体的差分矢量和1组两个随机个体的差分矢量来扰动个体的进化，这样就更大程度上提高了个体信息的共享程度，个体信息共享的公式为

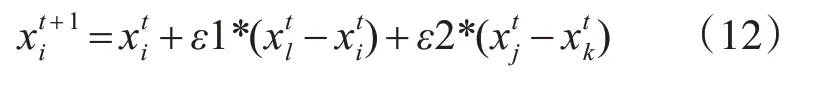
其中，ε1，ε2 分别是［0，1］上服从均匀分布的随机数，是在种群中随机选择的三个个体。这样，当产生的随机数大于0.5时，利用式（12）替换FPA 算法中的局部搜索方程进行个体间的信息共享。

3.4 ABFPA算法步骤

根据以上分析，ABFPA 算法的具体实施步骤如下。

step1：对ABFPA 算法的参数n、p、D、Max_iter赋初值；

step2：求解每个解的值，并记录所有值中的最小值或最大值和其相应的解

step3：如果p＞rand，执行全局搜索，并判断新产生的解是否越界，如果越界做越界处理；

step4：如果p＜rand，生成随机变量r；

step5：当r＜0.5，则执行step6，否则执行step8；

step6：利用式（10）对个体的位置进行更新；

step7：对step6 的个体再运用式（11）对其位置进行更新；

step8：采用式（12）对个体的位置进行更新；

step9：对step7 或step8 产生的新解做越界处理；

step10：求解step3或step7或step8产生的新解的值，并记录所有值中的最小值或最大值和其相应的解；

step11：如迭代次数大于阈值Max_iter，则进化结束，并输出所有解中的最优解和其相应的适应度值，否则，转step3继续演化。

从上述ABFPA 算法的进化过程可知，ABFPA算法与基本FPA算法的框架基本类似，但对其局部搜索部分进行了改进，以0.5的概率进行二分叉，一部分进行自适应搜索中心高斯变异和指数变异，另一部分增加了进行信息共享的个体。

4 实验仿真及分析

为了验证本文算法的有效性、可行性和正确性，本文对四类典型的优化测试函数（求解问题）进行求解，函数的详情见表1，且本文对所求函数的解都是求其最小值。为了全面客观评价新算法的性能优势，本文运用新算法与现有经典的改进FPA算法对比实验及分析，具体包括：1）收敛精度对比分析；2）非参数统计检验；3）稳定性和收敛速度对比分析，还包括基本FPA算法的对比。

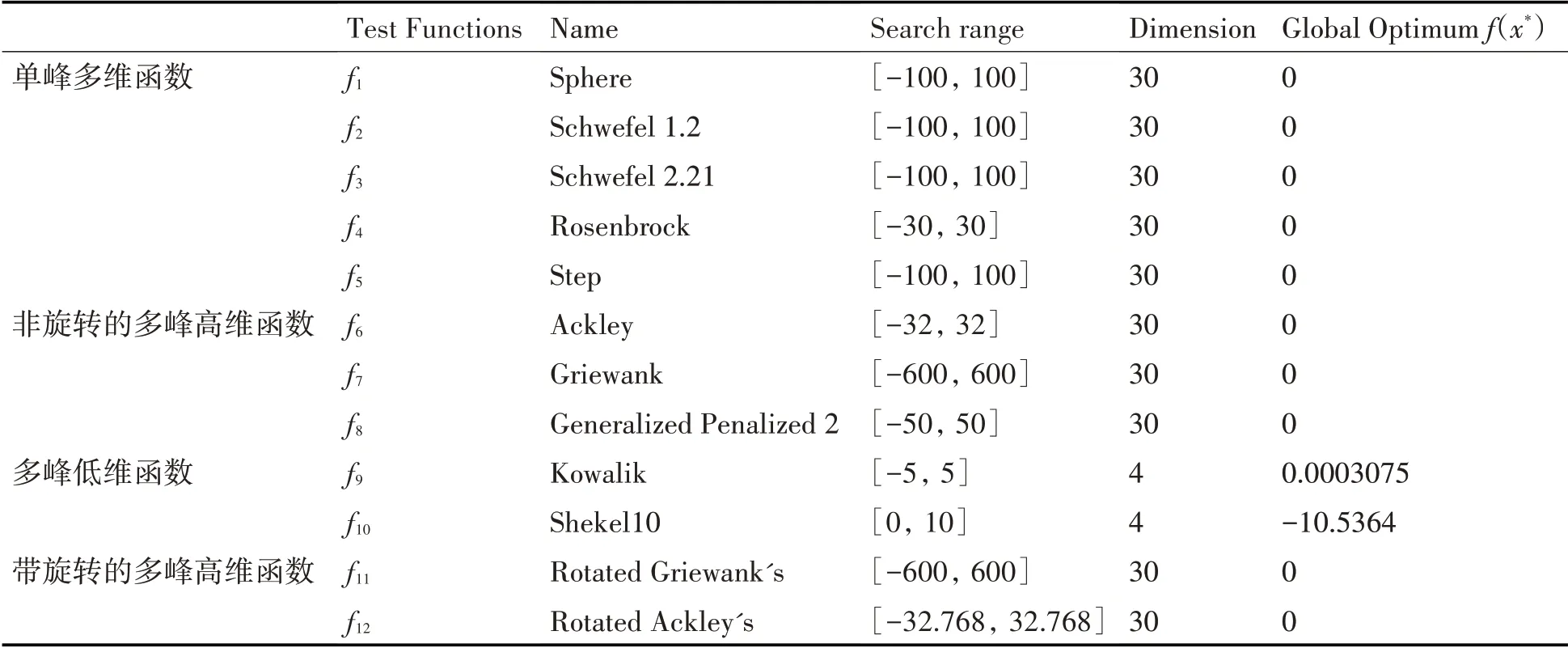
表1 本文采用的典型测试函数

4.1 解的质量对比分析

为了测试ABFPA 算法与现有经典的改进FPA算法在性能上是否具有不错的竞争力，本文选用目前有代表性的四种改进算法进行对比，分别是混合差分进化花授粉算法（a hybrid differential evolution-flower pollination algorithm，DE-FPA）［14］，基于精英反向学习的花授粉算法（Elite Opposition-based Flower Pollination Algorithm，EOFPA）［15］，改进的花授粉算法（Modified Flower Pollination Algorithm，MFPA）［16］，基于广义反向学习的改进花授粉算法（Modified Generalised Oppsition-based Flower Pollination Algorithm，MGOFPA）［16］。

本文的所有参数值分别设立为种群大小n=50，最大演化次数Max_iter=200；所有算法的参数p取相同的值0.8，其他参数取自相关文献中；DE-FPA 算法的参数CR 和F 分别取值为0.9 和0.5。为了降低实验偏差，每种对比算法在其每个求解问题上都单独执行30 次。各种对比算法的寻优结果如表2 所示，其中“-/≈/†”符号分别表明本文算法的收敛精度低于、相当于或高于对比优化算法，“w/t/l”符号分别说明ABFPA算法与对比算法对比，在求解问题上，有w 个优化结果好于比较算法，有t个寻优结果与比较算法相当，有l个优化效果劣于比较算法，最优结果用加粗凸显。

对表2进行分析可知，在12个函数中，ABFPA、EOFPA、MGOFPA 算法各自取得7 个、5 个和1 个理论解，其他算法都没取得理论解，这表明ABFPA 算法的寻优能力明显好于其他算法。算法具体在4类求解问题上的求解结果是在第1 类测试函数上，ABFPA、MGOFPA 和EOFPA 算法分别获得了4 个、1 个和两个理论解，其他两个算法均没有达到理论解，这表明ABFPA 比对比算法更适合用来求解这类问题；对于第2 类多峰高维函数，ABFPA 算法与EOFPA 算法的效果基本持平，优势不是很大，但要优于其他对比算法，且从表4 中的函数f7的平均迭代次数可知，ABFPA 算法的求解速度要显著快于比较算法；在第3 类低维多峰的函数中，ABFPA 算法优势不大；在第4 类多峰带旋转的高维函数上，ABFPA 算法和EOFPA 算法性能相当，但远远好于其余算法。ABFPA 算法的收敛性能总体上要明显地优于对比算法，展示出了较强的竞争力。

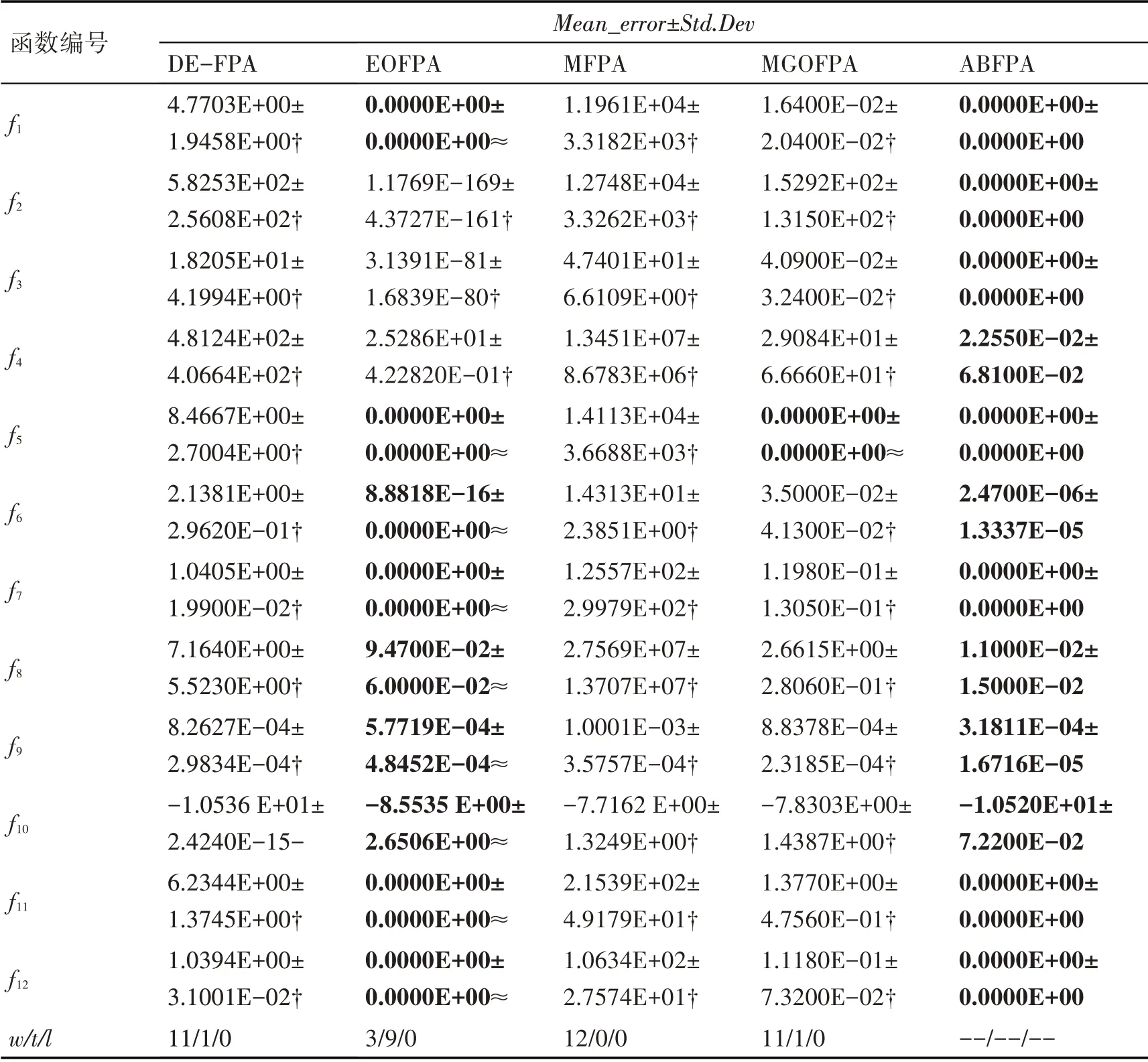
表2 5种改进算法的优化均值偏差和标准差

4.2 Friedman检验

为了更客观评价对比算法的综合性能，本文采用非参数统计检验（Friedman 检验）进行实验对比分析，其结果如表3 所示。对比算法的Rankings 值越小，其性能表现越突出，则排名越前。

从表3 中可知，ABFPA 算法的Rankings 值最小，在所有对比算法中，排在第一位，这表明ABFPA 算法的整体性能好于其他算法，具有良好的角逐力。

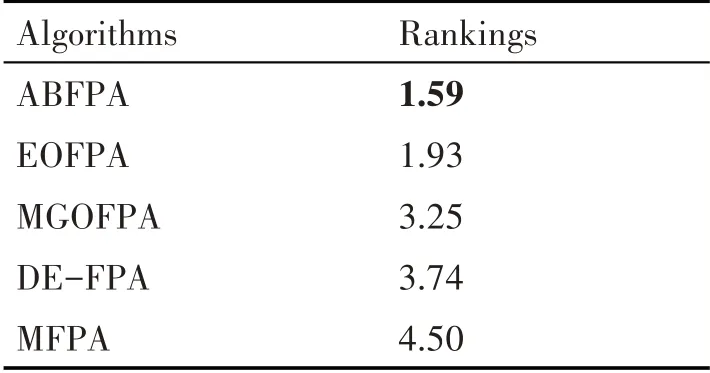
表3 5种FPA的Friedman检验（D=30，4）

4.3 鲁棒性和收敛速度对比分析

为了对ABFPA 算法的稳定性和收敛速度进行分析，验证其稳定性和求解速度的优势，实验结果如表4 所示。本文在每个求解问题上都设置了一个寻优精度边界值，若每种对比算法收敛到上述设定的阈值（边界值）且进化代数已大于一定的代数（本文设置为3000），则断定该算法对该求解问题寻优失败；其他参数设置同上，对比算法在每个求解问题上独立执行30 次；计算出SR（执行成功率，执行成功率=算法找到求解精度边界值所需要的代数/算法总的执行代数）值和mean_iter（平均进化代数）值，对比算法的SR 越大且mean_iter 越小，其性能越优，表4 中符号“NA”表示对比算法寻优受挫，最优结果用加粗凸显。

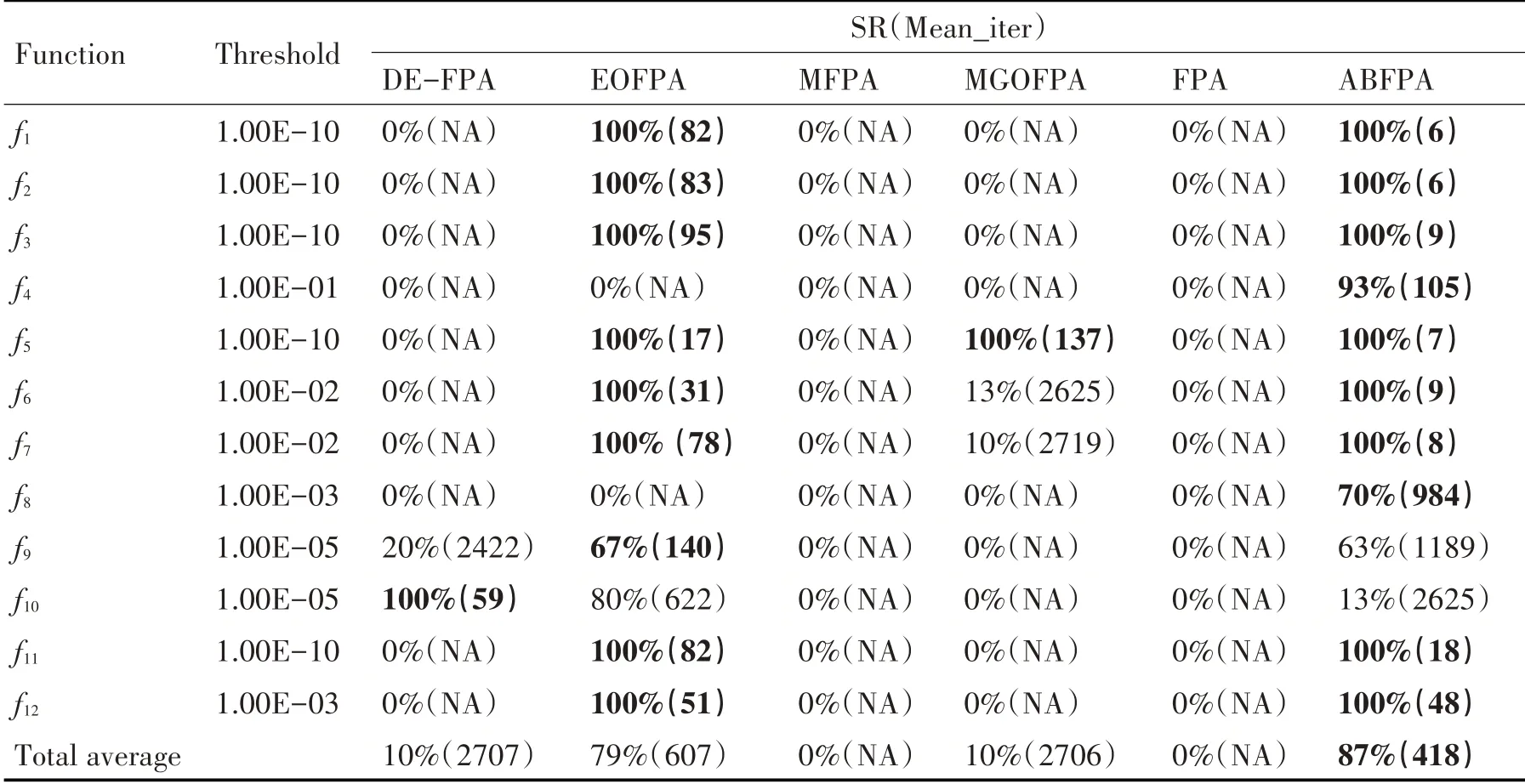
表4 6种算法的寻优成功率及平均迭代次数

从表4 的最后一行的平均寻优成功率和收敛迭代次数可以看出，FPA 和MFPA 算法的平均寻优成功率为0%；ABFPA 的寻优成功率为87%，均收敛迭代次数为418，较明显地优于对比算法。这说明ABFPA 算法的稳定性最强，ABFPA 算法的求解速度是所有算法中最快的。

5 结语

本文对基本FPA 算法的搜索策略进行了理论分析，发现其存在着的不足，制约着该算法的优化性能。为了提高其收敛能力，本文提出了一种自适应骨干花授粉算法。为了验证新算法的有效性和先进性，从解的质量、鲁棒性和收敛速度等多方面进行了实验对比分析，实验结果验证了改进算法是行之有效的。通过较丰富的实验结果证明，与具有代表性的其他改进算法相比，新算法的优化能力具有一定的优势。

在今后的工作中，如何利用新算法来处理能源、运输等实践中各类复杂的优化问题进行进一步研究。