求解SDCP 模型问题的人工蜂群算法研究*

牛佳惠 肖 宁 王煜东

（1.陕西职业技术学院人工智能学院 西安 710100）（2.国网咸阳供电公司 咸阳 712100）

1 引言

随 机 相 关 机 会 规 划［1～2］（Stochastic Dependent-Chance Programming，SDCP）是随机规划的一个子模型，是在随机环境下，决策者以极大化随机事件成立的机会（概率）为目标而提供最佳策略的一个不确定模型。如何高效求解SDCP 模型问题，一直是存在于经济、管理、最优控制等领域中的热点研究方向。

在实际的含有随机不确定因素的水土资源的最优配置、电力系统优化、无线传感网络的路由选择、作业车间调度、路径优化等应用方向中，SDCP问题不难提取，而SDCP 问题所表现的随机性及非线性导致了它难以求解，因而，研究者仍在继续探究着SDCP 这类问题的更优的求解途径。现在，各类智能计算技术在高速发展的算力平台的助力下，可以计算常规的或传统的方法很难实现的繁杂问题。SDCP问题的有代表性求解算法是基于遗传算法（Genetic Algorithm，GA）［1～3］，但因该算法自身的一些缺点，如，遗传操作过程复杂、程序需要控制的变量多、计算耗时、计算量大及容易早熟等等，探究更为有效的SDCP模型问题的求解途径仍旧为研究人员的关注点。

2005 年，Karaboga 提出人工蜂群（Artificial Bee Colony，ABC）［4］算法，为蚁群算法、微粒群算法之后的又一种仿生智能算法，如今已是智能计算的一个重要组成部分，同微粒群算法、遗传算法等群体智能算法相比较，它具有参数少、结构简单、易实现，并在整个寻优阶段，局部、全局搜索在每次迭代中都会进行，这一特点提高了该算法获得最优解的概率，这在很大程度上阻扰了发生早熟等优点，从算法的提出到如今的不足十五年，ABC算法在最优控制等领域中的应用得到大量的研究者的研究和关注［5～15］，然而，至今国内外文献资料只有本文作者发表的有关蜂群算法在随机规划问题求解中的应用研究的论文［16］，本文就是把随机模拟技术和人工蜂群算法相融合求解随机规划中的SDCP 模型问题，本论文算法的优化效果通过代表性的算例加以检验，同时它也为其它不确定环境下寻优提供了思路。

2 SDCP模型

SDCP单目标模型形式如下：

式中：ξ，x分别代表随机向量和决策向量，f（x）=pr｛hk(x,ξ)≤0,k=1,2,…,q｝，不等式组：hk(x,ξ)≤0,k=1,2,…,q是对随机规划的目标事件的描述，gj(x,ξ)≤0,j=1,2,…,p代表了随机不确定环境。该模型描述了在随机环境gj(x,ξ)≤0,j=1,2,…,p约束下使得事件hk(x,ξ)≤0,k=1,2,…,q成立的机会达到最大。在随机环境下，一个事件的机会等于与该随机事件相容的概率，这就是不确定原理所描述的内容，它是求解SDCP 的理论基础。

在管理目标与部分优先结构给定后，可通过极小化与本目标的正或负偏差，获得FDCP 目标规划描述如下：

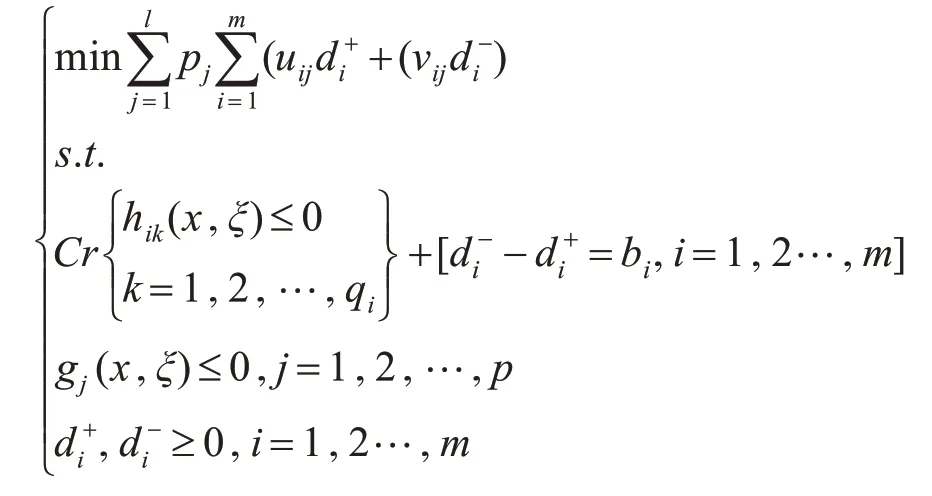
这里，gj描述了随机环境中的约束函数；pj描述了优先系数，代表各个目标的相对重要性，且对于∀j，有pj≫pj+1；第i个目标小于、大于目标值的偏差用代表；目标约束的数量用m 代表；p 代表系统约束的数量；1 代表了优先级的数量；目标i 的函数值由bi代表；hik代表了实值函数；uij、vij分别描述了目标i的第j个优先级的正、负偏差权重系数。

3 人工蜂群算法

2005 年，Karaboga 提出人工蜂群算法，它也是基于仿生智能的一种启发式算法，该算法受启于蜂群的协作觅食，不断探索蜜源的行为，以找到花蜜量最大的蜜源为目标，完成优化问题的求解。

在该算法中，整个蜂群由三类角色的蜜蜂组成：雇佣蜂、侦察蜂和观察蜂，它们在觅食中分工合作，不断迭代，其中，雇佣蜂的数量是整个蜂群的二分之一，同具体的蜜源相对应，雇佣蜂以跳摇摆舞的形式来与其他的个体分享蜜源信息，观察蜂数量上也是占蜂群总数的二分之一，它们等候于舞蹈区，通过分享雇佣蜂的信息对蜜源完成挑选，雇佣蜂们总能根据自己记忆中的最优位置并在其周围进行探测与侦查，丢弃食物源变为侦察蜂的雇佣蜂的工作则是开始在蜂房周围随机地探索新食物源。

在ABC 算法中，最优化问题的求解就是在问题空间上不断搜寻最优的数据使得目标函数达到最优。在维数为D的问题空间，食物源的位置对应了优化问题的候选解，蜜源的浓度则代表了每个候选解的适应度，食物源的数目等于雇佣蜂和观察蜂数目的和，表示为CN，若第i 个食物源的第n 次迭代的位置表示为xi=[xi1,xi2,…xiD]，则该食物源i的初始位置利用式（1）在搜索空间随机产生：

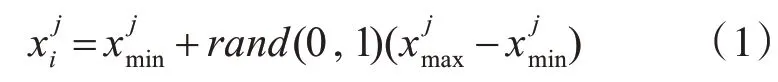
雇佣蜂根据式（2）在当前位置周围探测与侦查潜在食物源：

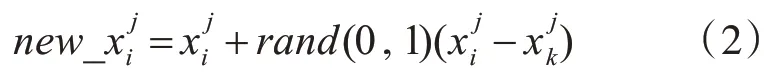
其中的k（k≠i）代表在蜜源里随机选择一个蜜源k；若新的蜜源new_的适应度好于，那么通过贪婪机制选择保留该较好解。所有的雇佣蜂完成了式（2）的运算之后，则将蜜源信息带回蜂巢并通过舞蹈的方式进行分享。观察蜂依据雇佣蜂所分享的花蜜信息，依照式（3）选择一个蜜源：

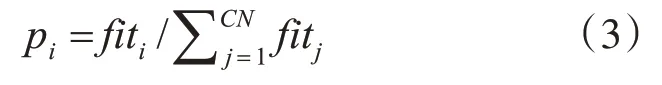
其中，fiti表示第i 个潜在解的适应度值，pi则代表了食物源i被选中的概率。

以寻找最小化问题为例，潜在解的适应度值依据式（4）完成：

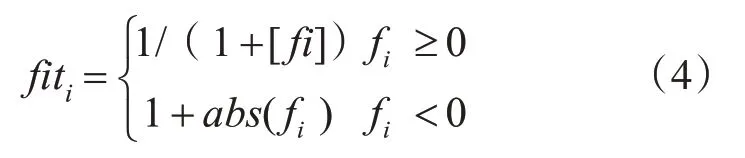
其中，fi代表了第i个潜在解所对应的函数值。

所有的雇佣蜂和观察蜂全部完成了搜索，然而食物源相对应的适应值在预定的number 次搜索，并在限定的食物源的改进次数limit 次仍没取得更好的食物源，则说明该潜在解已经沦为了局部最优解，则该食物源被丢弃，而与该食物源所对应的雇佣蜂转变角色成为侦察蜂，它将依据式（5）继续搜索新的食物源。

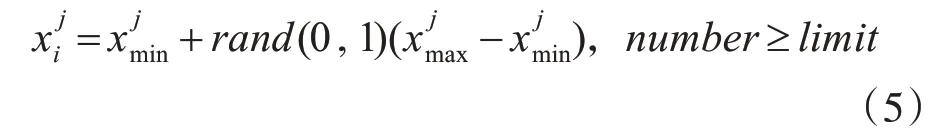
综上，使用ABC 算法寻优的要点是雇佣蜂的任务是负责搜索食物源；观察蜂的任务是依据雇佣蜂所分享的花蜜信息，然后观察蜂以指定的概率值完成对食物源的筛选；若某蜜源被丢弃，那么生成一个侦察蜂与随机产生的新食物源相对应。

4 嵌入随机模拟的ABC 算法求解SDCP模型问题

SDCP 模型问题求解时，通过使用人工蜂群算法在解空间进行寻优，在不断地迭代时需完成求解随机适应度值，适应度值的计算离不开随机机会函数的计算，而利用随机模拟技术可很容易地进行计算，在利用ABC 算法进行寻优时，它主要为算法的初始化及所有迭代中均需要随机模拟的概率估计算法来实现花蜜量的计算。

4.1 随机模拟的概率估计算法

常规的解析法很难计算随机事件的机会，现通过随机模拟求解事件的机会。

已知量ξi（i=1，2…m）随机变的概率分布函数用ϕi（i=1，2…m）表示，X 代表给定的决策向量，则计算随机事件的机会如下：

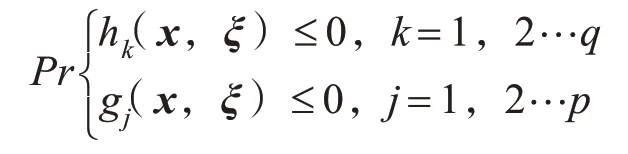
下面给出随机模拟的概率估计算法的基本流程：

步骤1：N′=0；

步骤2：利用概率分布函数ϕi，生成随机变量ξi；

步骤3：若果hk（x，ξ）≤0 ，gj（x，ξ）≤0 ，则，N′++；

步骤4：步骤2～步骤3 共重复执行N次；

步骤5：将N′/N的值返回。

4.2 算法步骤

嵌入随机模拟的ABC 算法求解SDCP 算法的操作步骤。

步骤1：在D 维问题空间中对蜜源总数为ColonyTotal 的蜜源xi（i=1，2…ColonyTotal）初始化：雇佣蜂、观察蜂的数目均为蜜源数量的ColonyTotal/2，蜜源最大限制搜索的次数limit，最大迭代次数MaxLoopNumber，各个维度的上、下界，通过式（1）获得ColonyTotal个随机初始蜜源，并将雇佣蜂与其相对应，利用随机模拟概率估计算法计算适应度值，并对雇佣蜂位置、观察蜂位置、最好蜜源等初始化。

步骤2：雇佣蜂通过式（2）修改食物源信息，通过随机模拟概率估计算法计算给定的随机机会函数的值并计算适应度值。然后对新食物源实施评价：若新食物源：new_的适应度比的适应度更好，那么通过贪婪机制把目前的较好解进行保留，反之则保留。

步骤3：利用式（3）来获得雇佣蜂找到食物源被观察蜂追随的概率，然后观察蜂则依据该数值来挑选食物源。

步骤4：使用与雇佣蜂相同的搜索方式，观察蜂进行食物源的搜索，也就是通过随机模拟可信性估计算法计算机会函数值、花蜜量，再通过贪婪机制保留当前最好的食物源。

步骤5：检验各食物源的连续搜索记录即number 的值是否超过最大限制次数limit，如果超过，那么通过式（5）随机产生一个新的食物源，利用随机模拟概率估计算法计算随机机会函数值、适应度值，相应的角色转变：雇佣蜂转变成侦察蜂，仍然通过贪婪机制保留当前最好的食物源。

步骤6：判断此时的算法是否达到了已经给定的最高迭代次数MaxLoopNumber，若满足，则寻优结束，否则跳转到步骤2。

5 性能测试与效果对比

笔者借助于经典的文献［1］里的实例完成仿真实验。

例5.1对单目标的SDCP模型进行求解：

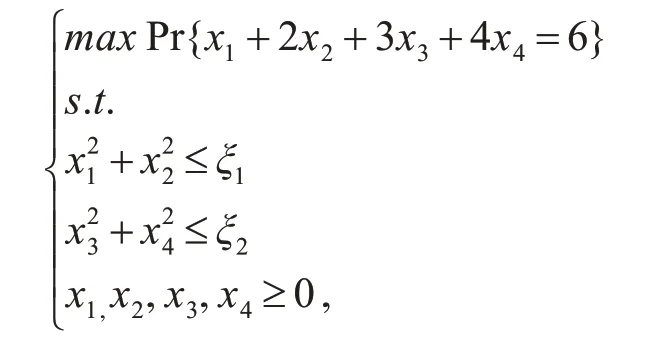
式中，ξ1服从正态分布N（5，1），ξ2服从指数分布EXP（4）。

例5.2对目标规划SDCP进行计算：

式中，ξ1服从从均匀分布U［3，5］，ξ2服从正态分布N（3.5，1），ξ3服从指数分布EXP（9）。

对于例5.1，事件为x1+2x2+3x3+4x4=6，该事件ε的支撑用ε*表示，ε*=｛x1,x2,x3,x4｝，对应的相关支撑用ε**表示，ε**=｛x1,x2,x3,x4｝，根据随机不确定原理，ε事件的机会函数：

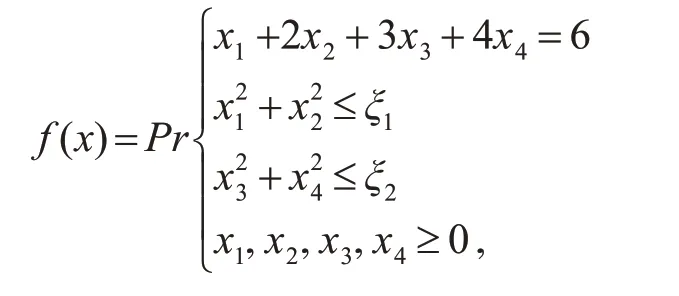
机会函数的值可通过概率估计算法求得。

算法中相关参数的设置等同于文献［1］：随机模拟次数RandTime 设置为5000 次；蜂群规模ColonyTotal 设置为30 个；迭代次数MaxLoopNumber 设置为300 代；运行次数设置为1。雇佣蜂和观察蜂的数目都设置为15 个，最大限制搜索的次数limit设置为15次。

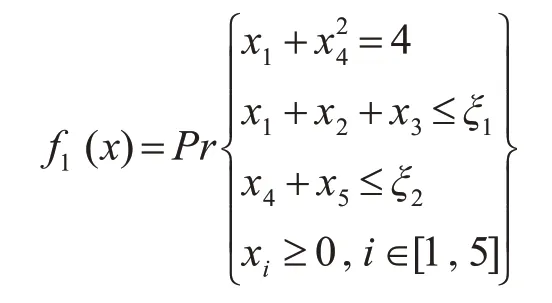
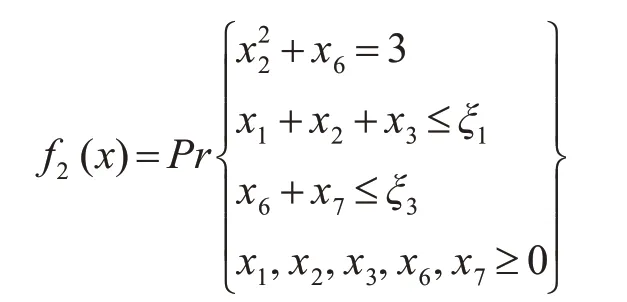
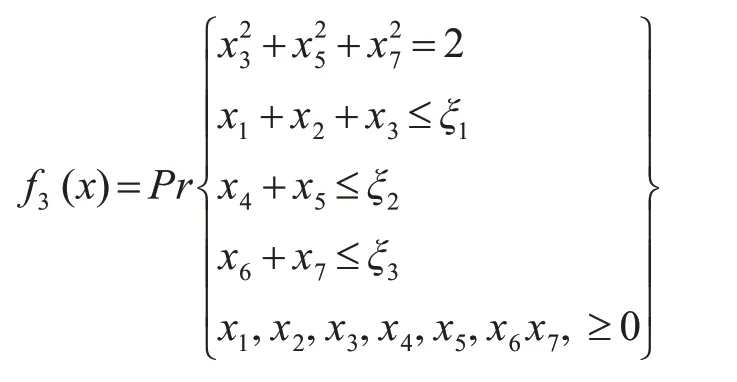
显然，它们的机会函数值可利用概率估计算法求得。

算法中相关参数的设置等同于文献［1］：迭代次数MaxLoopNumber 设置为1000 代；随机模拟次数RandTime 设置为6000 次；蜂群规模ColonyTotal设置为30 个；运行次数设置为1 次，雇佣蜂的数目设置为15个，观察蜂的数量设置为15个，最大限制搜索的次数limit设置为15次。

在内存容量8GB、CPU 主频3.0 GHz、操作系统Win10、Visual C++6.0为主要配置的台式电脑上完成验证。

在例5.1 中：嵌入随机模拟的ABC 算法运行的结果见表1，相比于文献［1］中的结果，本文的优化效果和利用了GA 算法的文献［1］的相当，但从迭代过程可知，文献［1］迭代到300 代取得了最优值94.7%，本文的ABC算法只要迭代到98代时就可达到，本文算法所得的最优值随着迭代次数增加的变化流程，进行每间隔10 代采样一次，迭代曲线如图1 所示，它直观地地展示了整个迭代过程：当迭代次数增加时，问题的全局最优值开始稳定。

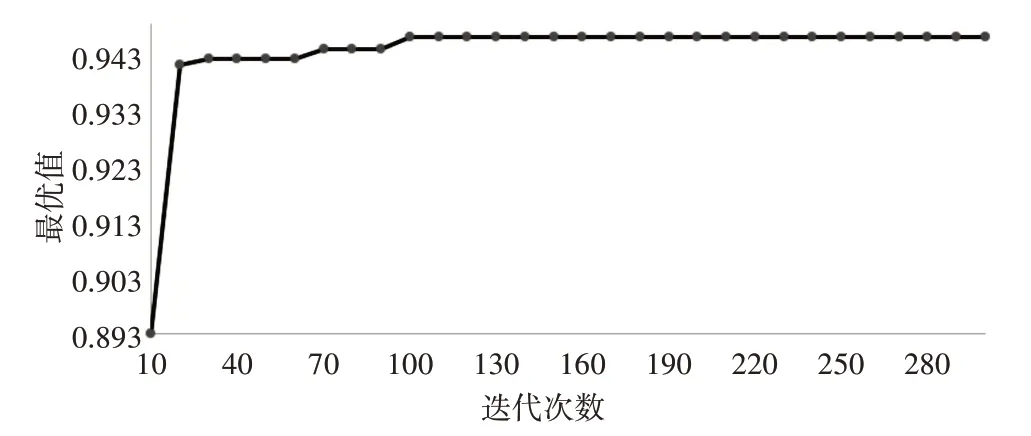
图1 实例5.1迭代曲线图

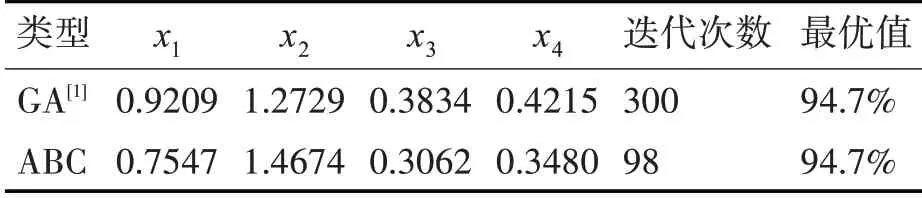
表1 实例5.1两种算法的优化结果

在例5.2 中：运行嵌入随机模拟的ABC 算法所得的最优解、最优值和结果如表2，同文献［1］中的求解结果相对比，显然优于文献［1］：文献［1］中第一、第二目标的负偏差、可以满足，但第三目标的负偏差的最终优化结果为0.048，本文算法优化的效果是所获得的最优解对应的所有目标负偏差均能满足。

表2 实例5.2两种算法的优化结果对比

6 结语

人工蜂群算法的策略是局部、全局搜索同时进行，这使得本算法具有了很强的全局寻优、收敛能力，本文主要讨论了嵌入了随机模拟的人工蜂群算法求解SDCP 问题，对照以GA 算法为核心的混合智能算法所得的求解结果，本算法求解质量显著，展示了它对于SDCP问题的求解优势。补充了通过ABC算法对随机规划问题求解研究的缺席，也拓展了该算法的应用研究范围。

值得一提的是，本文作者将ABC 算法对随机规划的另外两个子模型以及模糊规划模型进行了仿真实验，取得了与本文类似的结果，这为各类混合不确定规划问题的求解提供了参考，这是后期我们将开展的探究。