基于云安全模型的层次泛函网络整体学习算法*

徐胜超 邓斌涛

（广州华商学院数据科学学院 广州 511300）

1 引言

泛函网络内存在多个神经元结构，在泛函联结的前提下，网络结构内的神经元结构将实际问题转换处理为多种函数变换形式［1］，优化原有泛函网络内函数的非线性逼近能力。从层次结构来讲，泛函网络内存在输入单元层、处理单元层、中间单元储存层以及层次结构中的泛函联接［2］，层次化的泛函网络可由多个神经元结构拼接构成。从层次泛函网络的应用来看，网络结构已经运用到系统辨识、数据信息预测以及数值关系求解过程［3］，从应用性能来看，泛函网络内可运用到多个层次分析过程中，通过控制层次结构内的输出变量关系［4～6］，结合非线性代数方程实现网络学习过程的输出。云安全模型是一种解决分类问题的过程，针对云空间内的信任边界重组以及侵蚀过程，采用映射供应配置的处理来构建形成网络结构内的学习过程［7］。

国外研究泛函网络结构起步较早，研究人员以泛函网络结构内边缘计算层作为处理对象，收集并聚合边缘数据［8］，以时间与空间维度数值作为关联处理对象，形成了整体学习算法。国内研究泛函网络结构起步较晚，结合网络内深度可分离的卷积处理过程［9］，整理了网络态势要素以及态势数值的映射关系，形成整体学习算法处理过程。文献［10］中构建的整体学习算法，引用交替乘子将网络结构内的回归处理过程分解为多个独立求解过程，并设定网络传递参数，整合并迭代节点收敛数值关系，形成传递式的学习算法。文献［11］中构建的整体学习算法通过马尔可夫随机场分层处理网络结构内的聚类参数，并利用贝叶斯算法自适应处理该聚类参数，形成网络整体学习算法。经过阶段性的应用测试可知，现有的整体学习算法在相同的运行周期内的学习预测能力较差。为此针对上述存在的问题，本文以云安全模型作为支持，设计层次泛函网络整体学习算法。

2 基于云安全模型的层次泛函网络整体学习算法

2.1 定义云安全模型内指标的姿态值

云安全技术对网络资源、技术应用、数据信息安全等方面要求较高，由于云计算中心主要是虚拟技术，基于云的等级保护要求，对云计算信息系统安全等级保护测评有较大困难，云安全模型所提出的是云安全管理概念。云安全模型内存在多种预处理态势数据过程，在定义模型内指标的姿态值时，首先采用云服务器获取安全模型运行时的各类信息数据，结合统一规范化的处理过程，定义数据类别的敏感程度［12］，将含有敏感度参数的数值关系处理为正交矩阵，数值关系可表示为

上述数值关系中，A表示构造的正交矩阵，Q表示敏感程度参数，Q*表示敏感程度参数的秩，X表示正交矩阵内的随机向量，K表示云服务器内组建的随机向量。

在云安全模型结构内，近似奇异矩阵的分解复杂度存在传播性［13～14］。利用含有敏感度参数的数值关系的正交矩阵控制可用度参数的后验概率，控制矩阵可用度发生时产生的条件概率，并触发云安全数值模型内的安全事件［15］，在不同的可用度数值关系内设置不同数值大小的姿态值，触发姿态值条件如下：

上述姿态值关系中，CL(O)表示设定的可信度参数，CL(On)表示不同数值大小条件下的可信度数值关系，m表示云安全模型内可处理的安全事件。整理上述指标处理后的姿态基本参数，构建层次泛函网络逼近数值模型。

2.2 构建层次泛函网络逼近数值模型

整合上述计算得到的姿态基本参数和姿态值条件，并利用姿态基本参数构建一个三元约束数值关系，将该数值关系处理过程作为数值预处理步骤，在层次泛函网络内形成一个更新过程［16］，引用LDMLT 算法（Log divergence metric learning triplet constraint），该算法是指Log发散度量学习三元组约束算法，可以将层次泛函网络结构内的数值关系形成数值处理循环，数值循环可表示为

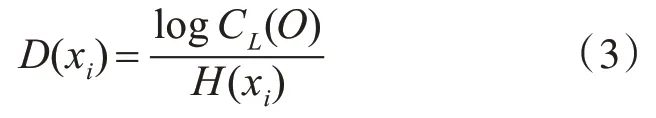
其中，D(xi)表示构建的数值循环处理函数，H(xi)表示姿态值的不确定熵函数，其余参数含义不变。在数值处理循环过程中，不同的观测周期内存在多个泛函网络最优解，选定极大似然处理过程确定网络结构中的最优解。

采用对数和的形式计算最优解参数的偏导，标记数值模型内的散度后验分布数值关系，形成特定的数值关系。为了控制标记后验分布内隐变量对数值循环的影响［17］，采用复杂混合弱监督过程形成标记筛选过程，标记筛选过程如图1所示。

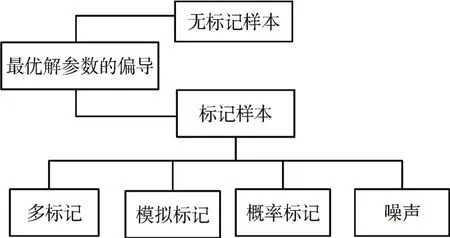
图1 构建的标记筛选过程

对应上述构建的标记筛选过程，在标定输出的后验分布数值关系内采用极大似然处理方法验证并标记输出不同数据类别，在构建逼近数值关系时，在标定的泛函网络结构内不断标记输出数值信息，并形成一个正则化框架，将多标记的数值属性处理为正则项［18］，引用惩罚函数输出各个数值集间的邻接矩阵，该邻接矩阵即为构建的逼近数值模型。在该数值模型的处理基础上，设计泛函网络整体学习算法。

2.3 完成泛函网络整体学习算法的设计

将图1 构建的标记筛选过程处理为泛函网络的数值层次结构，搭建层次泛函网络，在保留泛函网络拓扑结构所有优点的同时，还可以更好地构建泛函网络整体学习算法的设计。在设计其整体学习算法时，将同等属性数据集的泛函数值处理为输入单元，结合上述构建的数值逼近模型，输出泛函网络的输出表达，数值关系可表示为

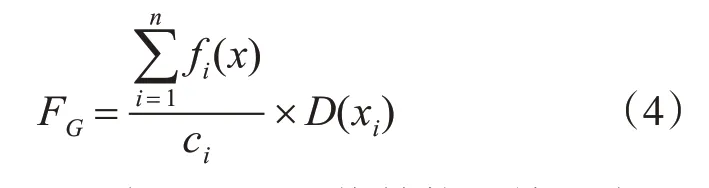
式（4）中，fi(x)表示泛函网络结构的输出表达函数，ci表示泛函网络的任意常量。在输出泛函网络的输出数值关系表达中，将数据信息存储为加密格式，并且需要将数据信息分开。在恶意代码防御过程中，可以了解恶意代码的检测、防御攻击的策略，结合云安全模型，整理泛化处理的实数空间，在该实数空间内重组并标记新的随机量［19］，整理随机量为数据集并将该数据集处理为初始群体，判断数值处理过程的适应度。将适应度数值关系联合代入至逼近数值关系内，为了控制标记数值样本的有效利用，将符合逼近数值模型的参数分类处理为数据样本标签，在实现算法的整体性时，利用该数据样本标签构建学习算法的邻近域［20］，最终输出整体学习算法形成的邻近域，最终形成整体泛函网络结构内的整体学习算法。综合上述处理过程，最终完成对基于云安全模型的层次泛化网络整体学习算法的设计。

3 算法测试

3.1 准备云安全模型测试数据

采用云安全模型的建站服务器开发包，安全数据选取云安全态势数据库中的数据样本，样本数据选定GitHub开源数据集，配置开发包的各项参数。

按照模型的特征维度，将云安全模型内的数据处理为多个序列属性，按照开发包的输出参数，定义采集数据的基本属性参数，如表1所示。

根据表1 定义的测试数据基本属性，控制测试数据集内包含多个子数据集，并在数据集内部定义多个学习任务，结合数据样本内的倒频频系数，整理得到模型特征维度，在控制上述属性数据在泛函网络中的误差时，设定算法验证逼近过程。

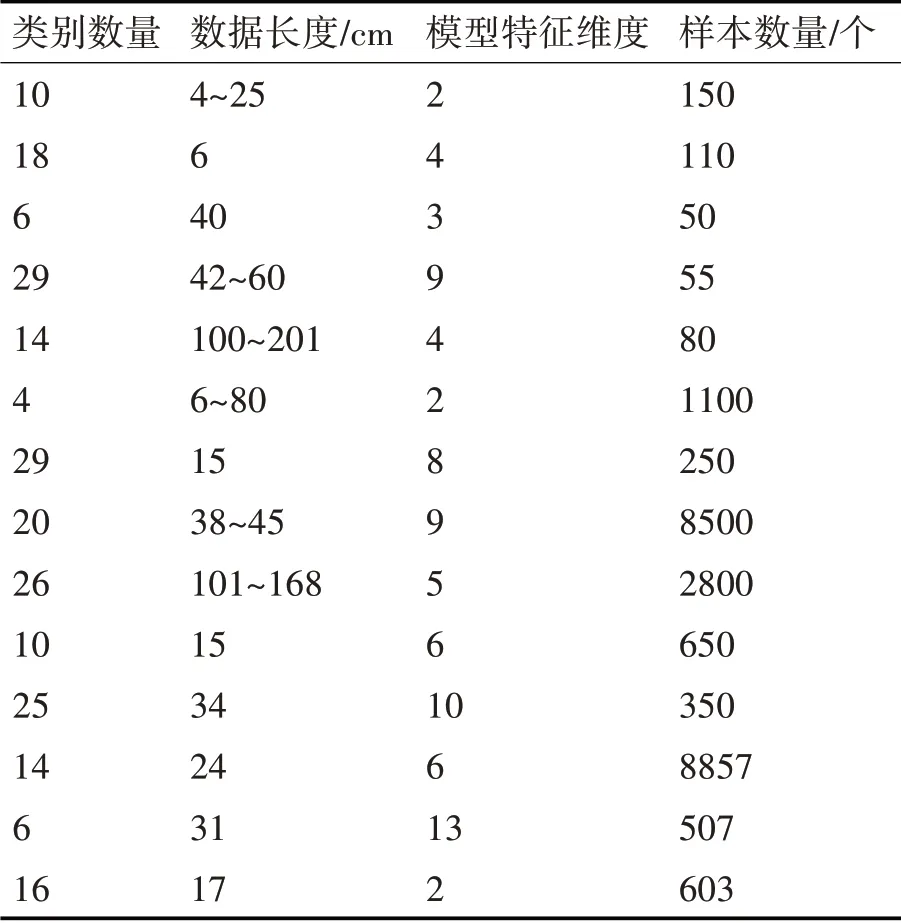
表1 测试数据基本属性

3.2 控制泛函网络结构层次误差

参照上述定义的云安全模型属性数据，应用进化算法结构化处理泛函网络产生的误差传播，误差传播过程可表示为图2。

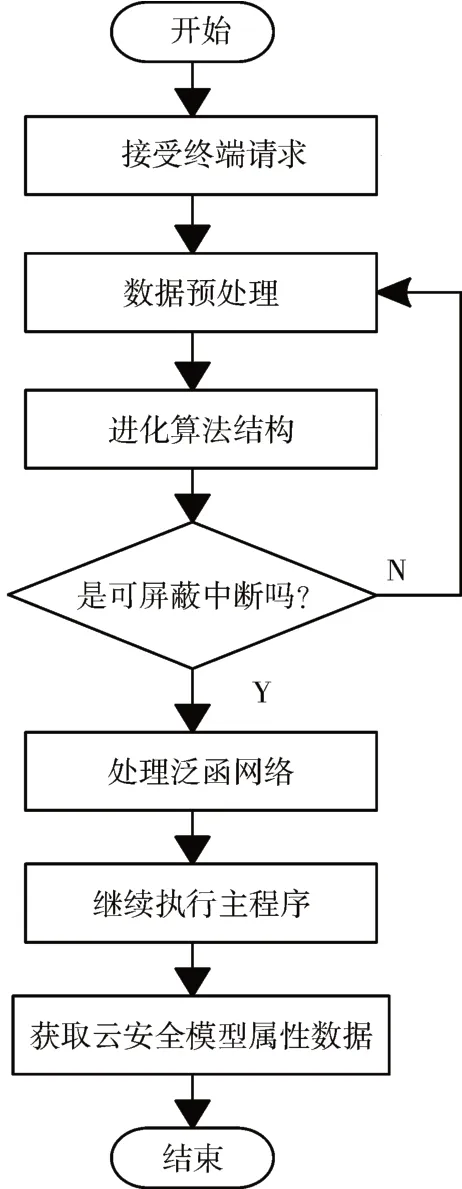
图2 结构内误差传播过程

为了验证结构误差传播的准确性，在数据属性范围内选定特定的二维函数作为泛函网络的学习样本，根据设定函数内的基本参数，采用神经元激发泛函网络内的神经元，定义泛函网络内的激发脉冲数量，在控制网络内的误差传输时，确定泛函网络内形成的激发误差，数值关系可表示为

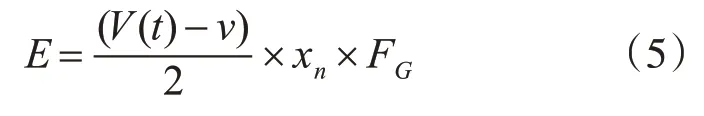
式（5）中，E表示网络传播过程产生的误差，V(t)表示网络结构的数值增加，v表示数据的传播速度，其余参数含义不变。依据式（2）在不同的可用度数值关系内所设置不同数值大小的姿态值，定义云安全模型内指标的姿态值，根据误差的传播周期，调整周期梯度下降形成的权重，并形成一个泛函网络的新脉冲，根据所构建层次泛函网络逼近数值模型，设定脉冲的激发形式，对脉冲产生一个激发过程。为了控制脉冲数值关系的精度，引用链式法则调整泛函网络中的贡献权重，结合泛函网络内的线性假设和所设计泛函网络整体学习算法，标定得到实际网络激发得到的脉冲数量。此时，泛函网络内存在两种激发数值关系，在控制误差的实际传播时，在泛函网络内的神经元单位内设定固定的脉冲激发时间，并变换上述式（5）为构造数值关系，可知设定的目标激发脉冲个数为10 时，泛函网络内实际产生的传播误差最小。

将上述控制结构层次误差参数作为测试环境的固定参数，选定文献［10］算法、文献［11］算法以及所设计的整体学习算法参与测试，选定相同的测试指标，判定三种整体学习算法的性能。

3.3 测试结果及分析

基于上述测试准备，以控制传播误差产生的基本参数作为算法的初始条件，可知在初始脉冲条件下，初始脉冲结构较为稀疏，故将初始脉冲数值由数值2 增加至10，在该处理过程中，控制泛函网络的序列时间长度为200ms，网络内存在的神经元单位为500。随机抽取三种整体学习算法的初始突触权重，为了控制整体学习算法的真实性，设定重复独立迭代的次数为20，记录单位周期内学习算法的学习时间，相同独立迭代次数下的不同整体算法所用的不同学习周期可准确反映算法效率的高低，传输效率是概括视频传输可靠性的重要指标之一，为了更好地验证层次泛函网络整体学习算法的可靠性能，需要对独立迭代次数与学习周期数量的关系进行验证，计算公式为

式（6）中，TJ表示学习周期结束时间，TC表示学习周期初始时间。根据式（6）求得三种整体学习算法所需的学习时间如图3所示。

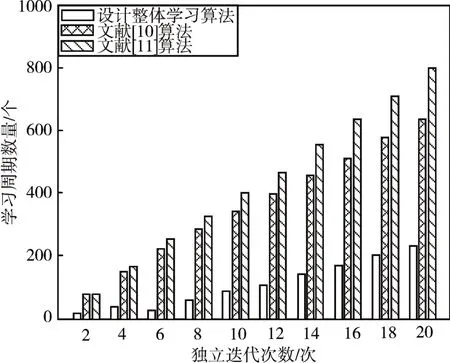
图3 三种整体算法所需的学习周期

根据上述整理得到的学习周期结果可知，在设定的重复独立迭代周期内，三种整体学习算法表现出了不同的学习周期数量，由上图所示的学习周期结果可知，三种整体学习算法的学习周期数量呈规律性增长，以独立迭代20 次后的学习周期数量作为最终整体算法的学习周期结果，文献［11］算法最终所需的学习周期数量为800，该种整体学习算法所需的学习周期较大。在相同的独立迭代次数内，文献［10］算法所需的学习周期数量为600，所需的学习周期较多。而所设计的整体学习算法所需的学习周期数量为200，与两种参与测试的整体算法相比，所设计的整体学习算法消耗的学习周期最小。

调用相同学习周期内的学习算法的处理过程，控制算法在同周期内处理泛函网络内的感知信息，并选定相同时间周期内时间长度为50ms的脉冲序列，设定网络结构内的神经元频率为4Hz，并将其余脉冲序列作为整体学习算法的干扰信号。为了更好地模拟层次泛函网络内的真实环境噪声，设定背景噪声的脉冲频率为泛函Poisson 分布形式，采用关键线索输入到泛函网络结构内的神经元单位内，控制干扰信号的神经元结构始终保持静默状态，设定学习预测周期为2s，可知三种整体学习算法到达固定的神经元频率时，则表示该种学习算法完成一次学习预测过程，整理三种整体学习算法在相同输入脉冲条件下产生的学习预测次数，计算公式为

式（7）中，Fo表示在相同输入脉冲条件下的学习预测频率，Fz表示频率在相同输入脉冲条件下的学习预测总量，根据式（7）求得学习预测次数，测试结果如图4所示。

整理相同学习周期下三种整体学习算法在设定神经元频率产生的学习预测次数，定义三种整体学习算法频率波动到神经元突出过程为实际学习算法的预测次数。由图4 所示的预测结果可知，文献［10］算法在相同的学习周期内产生的学习预测次数为3 次，该种整体学习算法的学习预测效果最差。文献［11］算法产生的学习预测次数为12 次，该种整体学习算法的学习预测性能较差。而所设计的整体学习算法到达设定的神经元频率数值为14，与两种参与测试的整体学习算法相比，所设计的整体学习算法的学习预测能力最佳。

4 结语

本文综合现有泛函网络整体学习算法的不足，以云安全模型作为技术支持，设计层次泛函网络整体学习算法。经过测试分析可知，所设计的泛函网络整体算法能够改善原有整体学习算法学习预测能力较差的不足。在未来工作过程中，希望所设计的整体学习算法能够为泛函网络提供理论支持。