基于局部多均值表示的K-近质心近邻分类算法*

周承如 熊太松 吴宏伟 杨园园 宋 君

（1.江苏大学计算机科学与通信工程学院 镇江 212013）（2.成都信息工程大学计算机学院 成都 610225）

1 引言

随着信息和网络技术的发展，日常生活中产生的数据呈现爆炸式增长的趋势，因此人们迫切需要一种有效的工具来对数据进行挖掘与处理。K-近邻分类（KNN）算法因其简洁有效性被看作数据挖掘领域十大经典算法之一［1］，被广泛运用于人脸识别、图像分类、计算机视觉和信息检索等方面［2～3］。许多提出的基于KNN 的分类算法虽然思想简单易于实现［4］，但其分类性能依然受到三个主要问题的约束：1）KNN 算法所选择的所有近邻点具有相同权重，导致不同近邻点对分类只起到了相同作用，降低了KNN算法的分类性能［5］。2）k值敏感性问题［6］，分类性能容易受到近邻个数k 值大小的影响，近邻个数k 微小的变化都会使分类获得不同结果。3）简单的最大投票原则［7］作为决策函数不能弱化近邻域中噪声点存在带来的影响，相反这些噪声点与有效近邻点具有相同分类贡献。

针对上述存在的问题，学者们在KNN 算法的基础上进行了大量的研究，同时提出许多改进算法。文献［8］提出了一种基于样本间距离加权的KNN 分类算法（The Distance-Weighted K Nearest Neighbor Rule，WKNN），在WKNN 中与测试样本距离不同的近邻可以获得一个自适应的权重，距离更近的近邻对于分类结果起到的作用更大，提高了算法的分类性能，然而WKNN 依然受到k值敏感性的影响。文献［9］提出了基于局部均值的KNN 分类（A Local Mean Based Nonparametric Classifier，LMKNN）算法，LMKNN 使用传统近邻的k 个均值作为新的近邻，可以获得更多的样本间信息来为分类提供帮助，并且减少近邻域中出现噪声点的可能性，然而该算法中不同局部均值具有相同的权重。基于协作表示［10］（Collaborative Representation Classifier，CRC）的分类是一种有代表性的低计算复杂度的分类方法，它有着特定的封闭解，对分类有着一定帮助。但是CRC 的分类性能容易受到噪声点和异类相似点的影响，在实际场景中的分类易受到干扰。

本文提出了基于局部多均值协作表示的K-近质心近邻分类（LMRKNCN）算法，LMRKNCN 结合了局部均值定理、质心准则和协作表示方法，旨在改善KNN 算法中存在的一些不足，同时提高分类性能。通过在一些UCI 数据集上与其他较新的算法进行实验比较，验证了LMRKNCN 的有效性与鲁棒性。

2 相关工作

首先统一介绍本文中使用的符号，对于一个训练样本集X，其中包含了L 种类别和共n 个训练样本，训练集特征维度为d，可表示为X=［X1，X2，…，XL］∈Rd×n。训练集中所有类别标签表示为C=｛c1，c2，…，cL｝，其中第i 类训练样本子集包含m 个样本可以表示为任意一个训练样本的类别标签是ci∈C，测试样本表示为y。

2.1 K-近邻分类算法

在KNN 算法中，对于一个测试样本y，y的类别标签c判别过程如下。

根据式（1）欧几里得距离计算y 与全部样本X的距离。

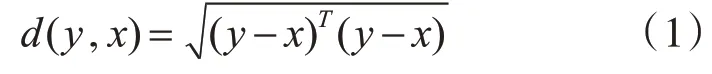
选取距离最小的k 个训练样本作为测试样本y的近邻。查找k 个近邻中每类样本的个数，将拥有近邻个数最多的类别标签分配给待测点y。

因此K-近邻算法的基本思想是根据距离大小找出关于待测样本点的k 个近邻，并遵循最大投票原则分配类别标签给待测点。

2.2 局部均值原则［9］

对于一个有k 个点的点集X=［x1，x2，…，xk］，这些点的k个局部均值求解如下：

使用局部均值作为近邻可以反映出样本间的相似性，获得更多有效的样本信息，同时减少了近邻区域中噪声点存在的概率，这些优势在小样本环境下更为明显。一些基于局部均值的分类算法［11］已经被证明具有优秀的分类性能。

2.3 近质心近邻原则［12］

对于一个待测点y，其近质心近邻点必须满足两个原则。距离最近原则：近质心近邻点应尽可能地靠近y，与y具有相似性。空间对称原则：近质心近邻点在空间上应尽可能地均匀分布在y 的周围。

给定一组测试点x={x1,x2,…,xp}，其质心点计算方法如下：

因此通过如下两个迭代循环可以找到关于待测点的k个近质心近邻点。

1）找出y的第一个近质心近邻点，该点也是KNN算法中的最近近邻点。

2）找出y 的第i 个近质心近邻点（i≥2）：计算训练集X中的每个点与之前已经找出的i-1个近质心近邻点,…,，然后计算这些近质心点到待测点y 的距离，选择其中距离最小的近质心点所对应的X中的点为。

使用近质心近邻能够获得样本间的空间分布信息，在基于空间距离的分类决策方法中，能够提高分类的准确性。

2.4 协作表示分类

其中常用的协作表示模型有：

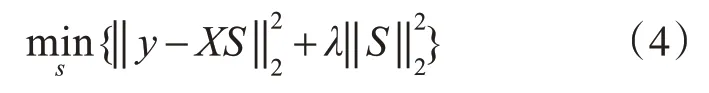
其中S是协作表示系数，λ是正则化参数。对式（4）求关于系数向量S的偏导，可以得到最优系数解为

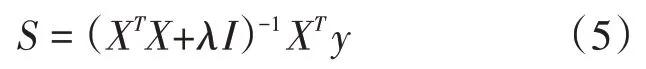
其中I是单位矩阵。使用基于测试样本与每类训练样本的残差大小作为分类决策函数，可表示为

将最小类别残差对应的标签分配给测试样本。

3 LMRKNCN算法

3.1 LMRKNCN基本思想

LMRKNCN 结合了局部均值和近质心近邻原则，首先求出每类训练样本关于测试样本的k 个近质心近邻，再计算k 个近质心近邻的k 个局部多均值近邻点。同时为了克服基于KNN 算法中不同贡献值的近邻却具有相同权重和简单的最大投票原则问题，LMRKNCN 继续求出k 个局部均值近邻点所对应的协作表示系数，协作表示系数相当于赋予近邻们不同的权重。最后基于样本间的残差大小作为该算法的分类决策函数，分别求出测试样本与每类训练样本中k 个局部多均值近邻点协作表示后样本的残差，将最小残差所对应的类别标签分配给测试样本。

3.2 LMRKNCN算法介绍

给定一个测试样本y，首先根据式（1）使用欧氏距离法计算每类训练样本与测试样本的距离。接着找出每类中距离测试样本最近的训练样本作为第一个近质心近邻点，也是传统KNN 算法中的第一个近邻点。根据近质心近邻原则依次找出剩余k-1 个近质心近邻。再通过局部均值原则式（2）计算出这k个近质心近邻的k个局部多均值。接着由式（5）求解所得k 个局部均值质心点对应的协作表示系数，用k 个近质心局部均值点协作表示测试样本。计算测试样本y与每类k个近质心局部均值点协作表示后样本的残差，将最小残差所对应的类别标签分配给测试样本y。LMRKNCN 算法具体步骤将以Matlab伪代码的形式进行说明。

3.3 LMRKNCN理论分析

LMKNN 与LMRKNCN 都是基于样本间的距离作为决策函数，然而两种算法所选择的近邻点对于分类结果起到的作用是不同。LMKNN中近邻点主要是k个局部均值点，根据式（2）求出测试样本y关于类别cj的k 个局部均值记作：…,]。测试样本y 与类cj中第i 个局部均值的欧氏距离为d(y,)。文献［13］对距离平方求解关于近邻的导数，求导结果表示了每个近邻的权重，也就是其对于分类的贡献比例。

LMRKNCN 使用测试样本y 与每类k 个近质心局部均值点协作表示后的残差作为分类决策函数：

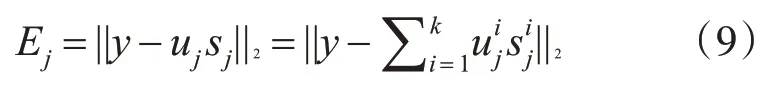
不同近质心局部均值点对于分类应该有着不同的贡献，在基于协作表示分类的方法中使用样本残差作为分类决策函数，可以直观地表示样本对分类起到的贡献。对式（10）求导，也就是求残差Ej关于近质心局部均值的偏导，求导过程如下：

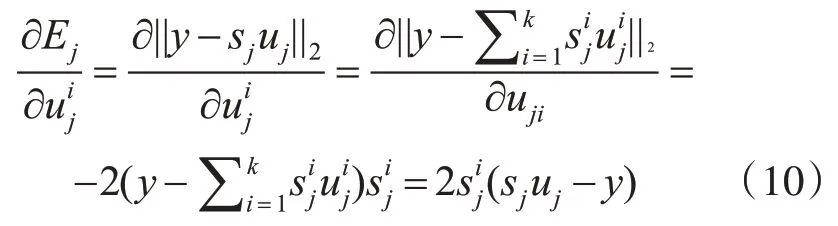
根据式（10）求导的结果可知，在基于样本残差的分类决策函数中，每个近质心局部均值点对应的协作表示系数也是不同。如果使用简单的最大投票原则作为分类依据，那么不同的近质心局部均值点对于分类只起到了相同贡献。 因此LMRKNCN 给不同的局部均值匹配一个协作表示系数作为权重，可以提高分类性能。

4 实验结果与分析

使用Matlab（实验矩阵）软件实现了LMRKNCN算法模型。为了验证LMRKNCN 的分类有效性，将其与KNN，LMKNN，KNCN 和LMRKNCN 相关对比算法在6组UCI［14］真实数据集上进行实验分析。表1详细介绍了数据集的相关属性。

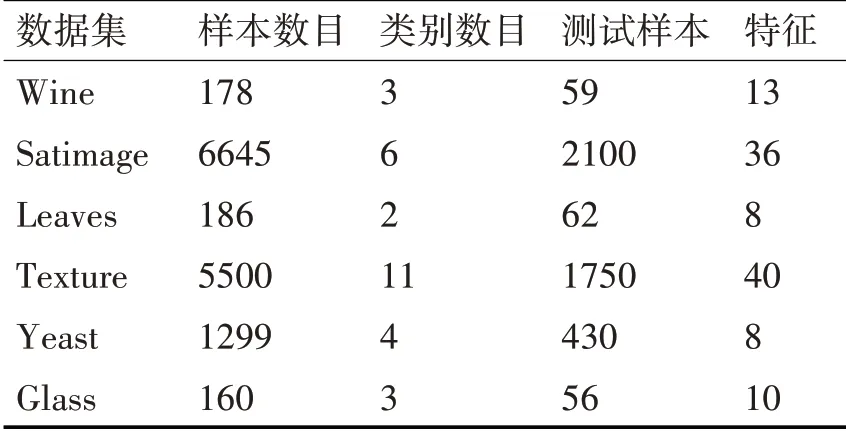
表1 数据集描述

为了客观地研究所提LMRKNCN 算法的分类性能，对每一个数据集进行10 次拆分，所有的样本每次都会被随机拆分成为测试样本和训练样本，以此来确保实验的分类效率和分类结果的可参考价值。通过改变所选取近邻的个数k 和可变参数λ，来研究LMRKNCN 与其他对比算法的分类错误率，旨在证明LMRKNCN 能够减少样本中噪声点存在带来的影响。近邻个数k 的变化范围是从1～15 并且步长为1，可变参数λ的数值范围设为λ∈｛0.001，0.01，0.1，1，10｝。在所有数据集上运行10次，取10次实验的平均分类误差作为最终的实验结果。

4.1 实验结果与分析

图1展示了所有方法在不同的k值下的分类错误率。

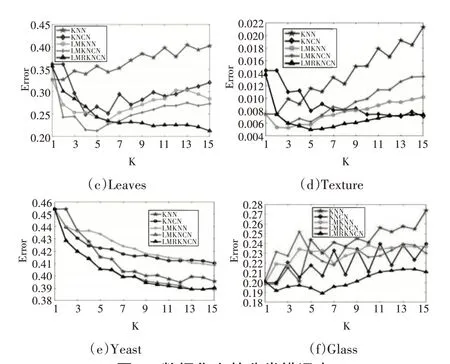
图1 数据集上的分类错误率

此外，为了更直观地展示LMRKNCN 与其余对比算法的分类性能，表2 列出了LMRKNCN 以及对比方法在真实数据集上的最小错误率和所对应的k值与对应的实验偏差。在每个真实数据集上的最优分类结果以及对应的分类算法被用黑色加粗加斜字体标注出来。每个数据集上的最优分类结果以及对应的分类算法被用黑色加粗加斜字体标注出来。

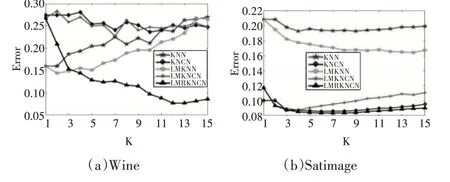
分析图中变化的分类错误率曲线可知：

1）在k值较小时，增大k值，LMRKNCN 的分类错误率呈现快速下降，随后趋于稳定的趋势。而其余对比算法的错误率随着k 值增大呈现无序变化或逐渐增大的规律。

2）LMRKNCN 的最低分类错误率通常在k 值较大时获得，而其余对比算法在k 值较小或k 为1时获得最低分类错误率。说明LMRKNCN 能够抑制k值敏感性问题。

3）LMRKNCN与对比算法相比，在实验所取的k 值范围内能够获得最低的分类错误率，对应着最佳的分类性能。

从表2 可知，LMRKNCN 的分类性能明显优于其余对比分类算法，尤其是在小样本数据集上。并且LMRKNCN最优的分类性能通常在k值较大时取得。又进一步证明LMRKNCN 对于模式识别具有较好的有效性，同时减少了噪声点给分类性能带来的影响。

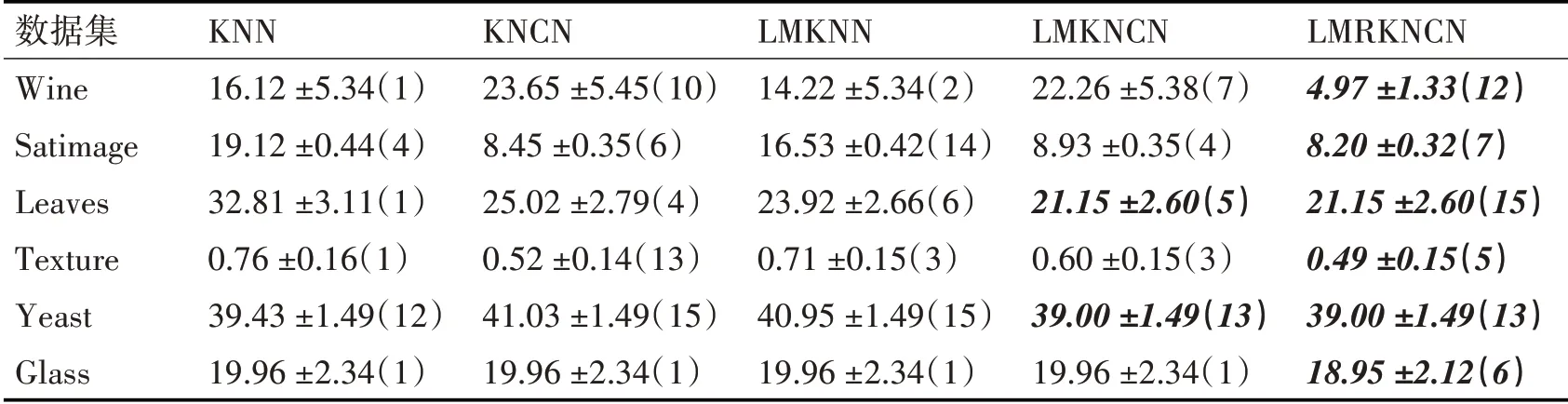
表2 最佳分类结果（均值±标准差%，对应的k值）

4.2 时间复杂度分析

对KNN，KNCN，LMKNN，LMKNCN和LMRKNCN算法的时间复杂度进行分析比较，进一步研究所提LMRKNCN 算法的分类性能。基于KNN 的分类算法，其运行时间主要由查找近邻点所需时间来决定，因此只需分析四种算法查询近邻点的时间复杂度。在时间复杂度的计算中，涉及到的符号：n 为训练样本数，d为样本的特征数，k为近邻个数，m为每类中的样本数，L 为类别数。由文献［15］可知，KNN 对测试样本进行分类的时间通过计算欧几里德距离寻找测试样本的k个近邻，因此KNN的时间复杂度为O（dn+kn+k）。在KNCN 算法中，根据近质心选择原则，对于一个待测点，查找该点的一个近质心近邻点最多需要进行n 次距离计算，n 次质心点和n 次距离进行比较，因此查找一个待测点的K-近质心近邻点的时间复杂度为O（2dn+kn）。在LMKNN方法中，对任意待测点，首先需要分别在每类中查找k 个近邻，在一个类别中需要进行m 次距离和m 次距离之间的比较，所需时间复杂度为O（dm+km），因此在有L 个类别的数据集上，LMKNN查找k 个近邻的时间复杂度为O（dn+kn）。对于LMKNCN 算法，对于给定的待测点，需要查找每类训练样本的k 个近质心近邻，这需要的时间复杂度为O（2dm+km），所以在有L 个类别的数据集上，一共需要的时间复杂度为O（2dn+kn）。本文所提算LMRKNCN 算法，同样使用近质心选择原则找出每类训练样本的k 个近邻，所以与LMKNCN 算法相同，时间复杂度为O（2dn+kn）。

为了更直观地展示，我们将所有算法的时间复杂度列入表3 中。观察表3，可以得出：LMRKNCN与其他对比算法的时间复杂度比较接近，进一步说明了LMRKNCN算法的可实施性。

表3 时间复杂度

5 结语

为了针对基于KNN 算法中存在的问题，提高基于KNN 算法的分类识别率，本文提出了LMRKNCN 算法。LMRKNCN 在KNCN 与LMKNN算法的基础上进行了改进，首先找出测试样本关于每类的k 个近质心近邻，通过近质心近邻求解局部均值，使用协作表示系数作为表示的自适应权重，最后使用基于样本残差分类决策函数，计算测试样本与每类k 个近质心局部均值近邻点协作表示后预测样本的残差，将最小残差所对应的类别标签分配给测试样本。为了改善在小样本情况下识别率容易受到k 值敏感性影响的问题，LMRKNCN 使用了近质心近邻和局部均值，近质心近邻可以将近邻更几何地分布在测试样本附近，同时使用局部均值可以减少近邻边境区域中噪声点对识别结果带来的影响。与LMKNCN 的不同在于，LMRKNCN 对所得局部均值求解协作表示系数并用近质心局部均值点协作表示测试样本，可以改善因简单的最大投票导致不同近邻之间无区分度的问题。将LMRKNCN 与KNN，KNCN，LMKNN 和LMKNCN 在多个真实数据集上进行对比实验，实验结果表明LMRKNCN 的分类性能优于其余对比算法，尤其是在小样本数据集中对分类具有有效性和鲁棒性。综上所述LMRKNCN 在模式识别领域是一种有效的分类算法。

在本文工作的基础上，笔者下一步将继续收集其余高维度数据集并对LMRKNCN 的分类性能进行验证，同时针对不同的数据集扩大k 的取值范围，来使不同数据集获得自适应的动态最优k 值和最佳的分类性能。