具有双曲余弦项的新型灰色预测模型及其在居民生活能源消费量中的应用*

马 娟 马 新 吴文青 胡荣春

（1.西南科技大学理学院 绵阳 621010）（2.西南科技大学信息学院 绵阳 621010）

1 引言

2017 年10 月十九大明确提出要“构建清洁低碳、安全高效的能源体系”。随着工业能源节能措施的实施我国工业能源增长趋势已渐缓，但随着我国城镇化建设进程加速以及居民生活水平提高使生活能源消费需求不断攀升，生活能源消费引起的碳排放愈加不可小觑。2020 年新冠疫情席卷全球，文献［1］指出疫情持久损害全球经济、重创全球能源需求、加剧能源贫困和能源不平等，能源政策的选择制约着国民经济和社会的发展，因此为能源规划和政策提供理论依据的能源预测已成为研究的热点。

近年来，能源需求预测的方法主要包括时间序列法、灰色预测、人工神经网络、遗传算法等，预测算法从单一的预测模型发展到组合预测模型。郑艳玲和吴亚茹在文献［2］中采用灰色预测模型GM（1，1）预测河北省能源消费；彭新在文献［3］中采用基于Elman 神经网络预测能源消费；程文荣在文献［4］中采用多元线性回归和GM（1，1）模型预测江苏省能源消费；汪京徽等在文献［5］中采用Holt 线性趋势模型和ARIMA 模型预测安徽省能源消耗量，夏杰和吴文青在文献［6］中采用组合灰色与神经网络模型预测的全国能源消费总量；李翼和桂预风在文献［7］建立基于IOWGA-Markov 的新型灰色指数组合预测模型预测我国石油消费比例；孙庆凯等在文献［8］中构建LSTM-MTL多元负荷预测模型进行楼宇综合能源系统多元负荷预测。其中灰色预测模型在能源预测中得到广泛应用，从1982 年邓聚龙教授在文献［9］中提出后围绕GM（1，1）模型开展了一系列研究，包括谢乃明和刘思峰在文献［10］中提出的离散灰色预测模型DGM（1，1）；崔杰、谢乃明、刘思峰等在文献［11～12］中提出的非齐次灰色预测模型NGM（1，1，k）；陈鹏宇在文献［13］中提出灰色作用量为bt+c 的非齐次模型NGM（1，1，k，c）；罗党和王小雷［14］提出耦合三角函数的灰色模型GM（1，1，T）；向希望等［15］提出含双曲时滞函数的单变量灰色预测模型HTGM（1，1）。

本文提出一种具有双曲余弦项的新型灰色预测模型HCGM（1，1），采用我国2008 年～2018 年居民生活能源消费量中热力、液化石油气、天然气和电力消费量，对居民生活能源消费量进行预测并检验预测精度。

2 HCGM（1，1）模型

2.1 一阶累加生成序列与累减序列

定义1：设原始序列X(0)={x(0)(1 ),x(0)( 2),…,x(0)(n)}，其中x(0)(k) ≥0,k=1,2,…,n，则X(0)的一阶累加序列（简记为1-AGO）记为X(1)，即

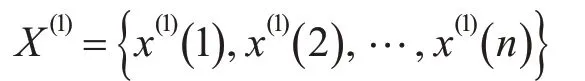
累减生成是累加生成的逆运算，一阶累减生成序列为

进一步，记X()1的紧邻均值序列为Z(1)，即

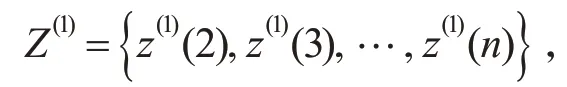
2.2 白化微分方程

定义2：灰色预测模型GM（1，1）的白化微分方程为

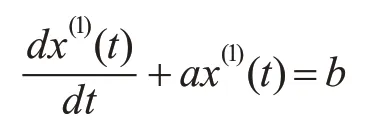
在灰色预测模型GM（1，1）的白化微分方程基础上，结合双曲余弦函数提出新型灰色预测模型HCGM（1，1），其白化微分方程为

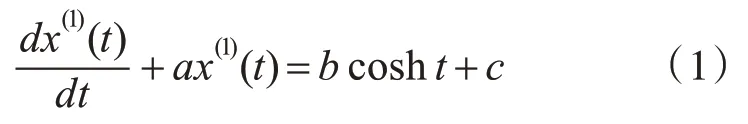
2.3 时间响应函数

定理1：新型灰色预测模型HCGM（1，1）的时间响应函数为

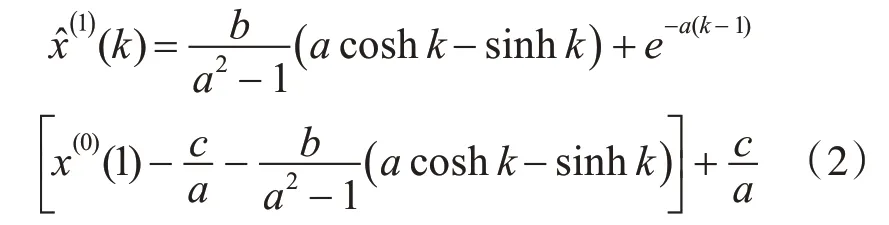
证明：

首先，求解HCGM（1，1）模型的一阶非齐次白化微分方程（1）对应的齐次方程：

的通解，得

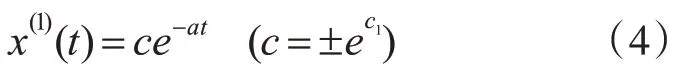
其次，使用常数变易法令c=u(t)，则

于是

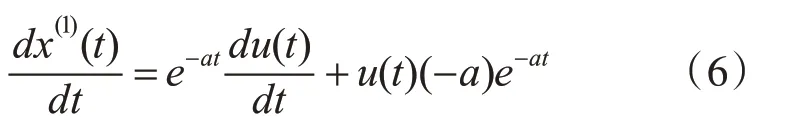
将式（5）和式（6）代入式（1）得

对u′(t)两端在区间［1，k］上进行积分，得到

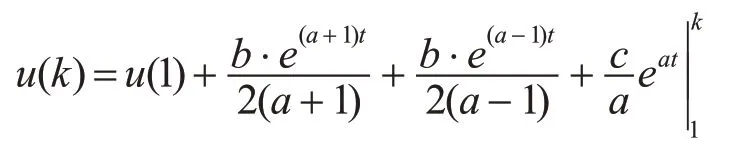
其中x(1)(1)=u(1)e-a且x(1)(1)=x(0)(1)，则u(1)=x(0)(1)ea，于是

最后，将式（8）代入式（5）整理得到

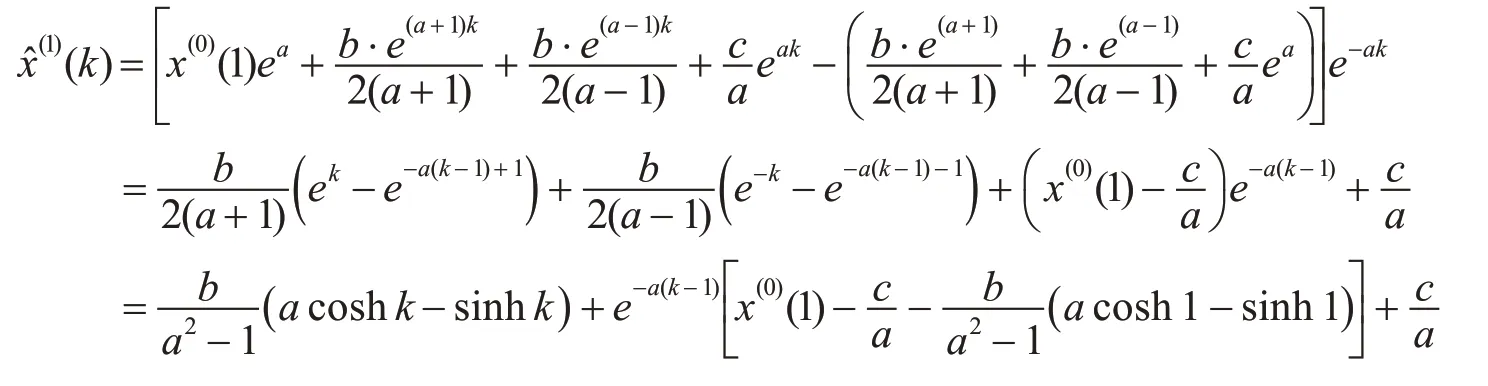
2.4 模型参数

定理2：新型灰色预测模型HCGM（1，1）的参数向量为

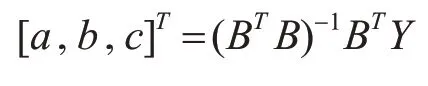
其中：

证明：

首先，对HCGM（1，1）模型的白化微分方程（1）两端在区间［k-1，k］上进行积分，得到

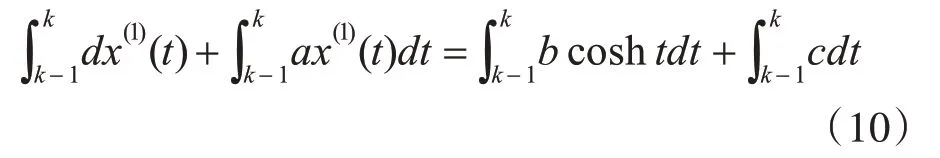
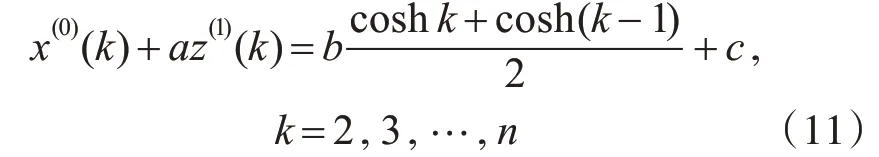
于是将式（12）更换为矩阵形式：

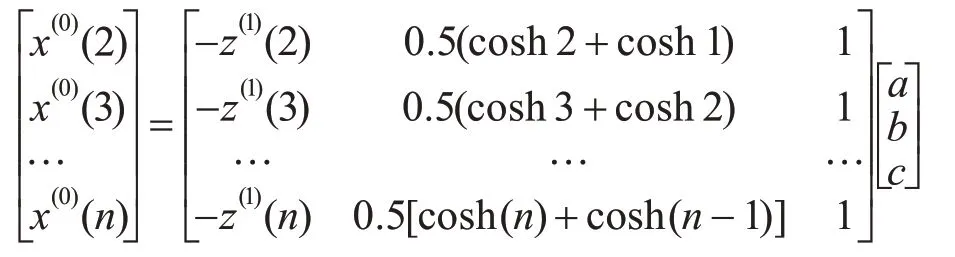
采用最小二乘法估计得到HCGM（1，1）模型参数向量[a,b,c]T=(BT B)-1BTY。

2.5 模型精度检验

使用均方根百分比误差RMSPE 来验证模型的可行性，评判标准为

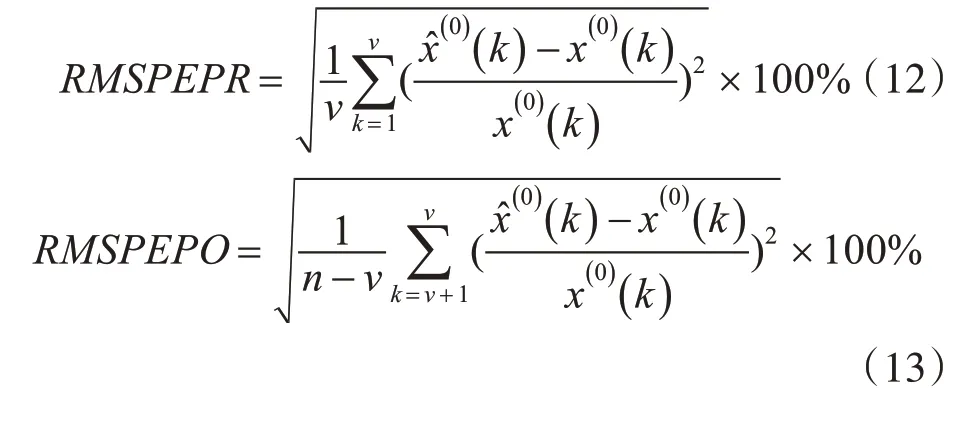
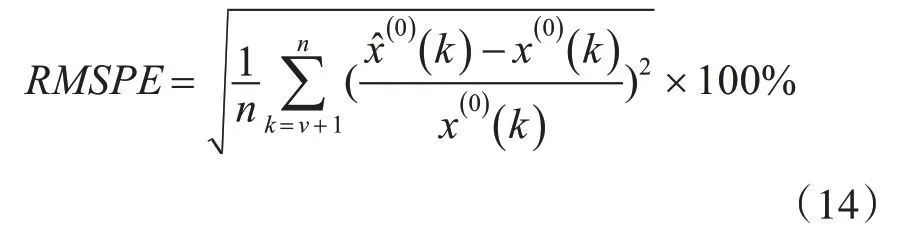
其中v是用于构建建型的样本数，n是样本总数。

3 模型在居民生活能源消费量中的应用

选取中国统计年鉴［16］中居民生活能源的热力、天然气和电力消费量为样本，分别采用灰色预测模型GM（1，1）、DGM（1，1）、NGM（1，1，k）、NGM（1，1，k，c）以及HCGM（1，1）进行模型仿真与预测误差比较。

3.1 热力

选取2008 年～2018 年我国居民生活能源热力消费量为样本数据，其中2008年～2017年数据用于建立预测模型，2018 年数据用于测试。五个预测模型求得的预测值以及均方根百分比误差值如表1 所示，模型预测结果比较及均方根百分比误差比较分别如图1、图2所示。

从表1、图1和图2可以看出：

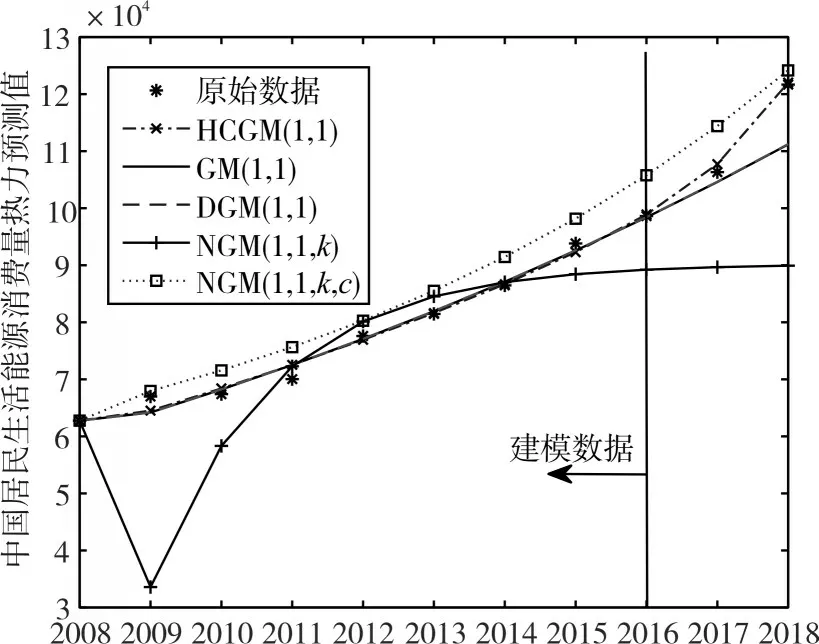
图1 热力消费量不同模型的预测图

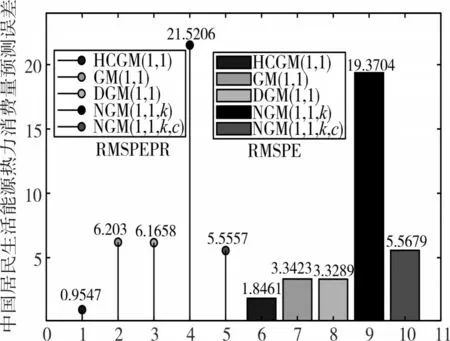
图2 热力消费量不同模型的预测误差

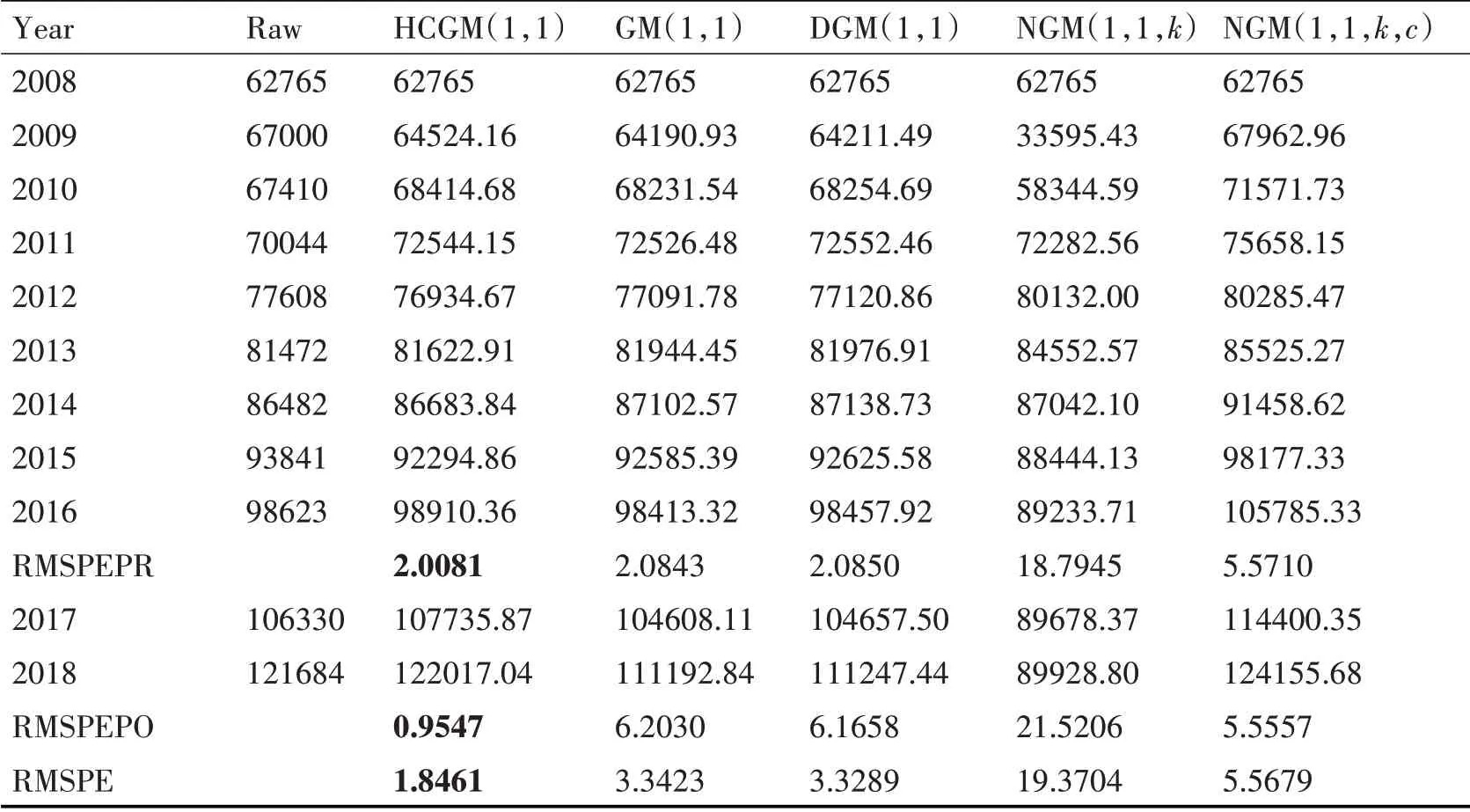
表1 热力消费量不同模型的预测值

1）无论是建模、预测还是总体的均方根百分比误差，HCGM（1，1）模型的精度都高于其他四个模型，因此HCGM（1，1）模型具有很好的预测能力，而NGM（1，1，k）模型的预测精度最差；

2）NGM（1，1，k，c）模型预测结果均高于真实数据，而其他四个模型预测结果在真实数据左右浮动，且HCGM（1，1）模型的预测值最接近真实值。

3.2 天然气

选取2011 年～2018 年我国居民生活能源天然气消费量为样本数据，其中2013 年到2017 年数据用于建立预测模型，2018 年数据用于测试。五个预测模型求得的预测值以及均方根百分比误差值如表2 所示，模型预测结果比较及均方根百分比误差比较分别如图3、图4所示。

从表2、图3和图4可以看出：

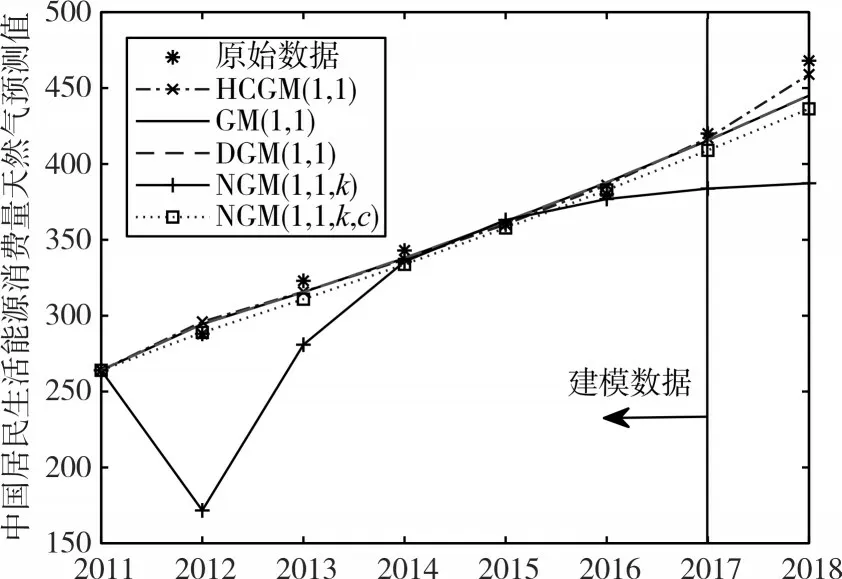
图3 天然气消费量不同模型的预测图

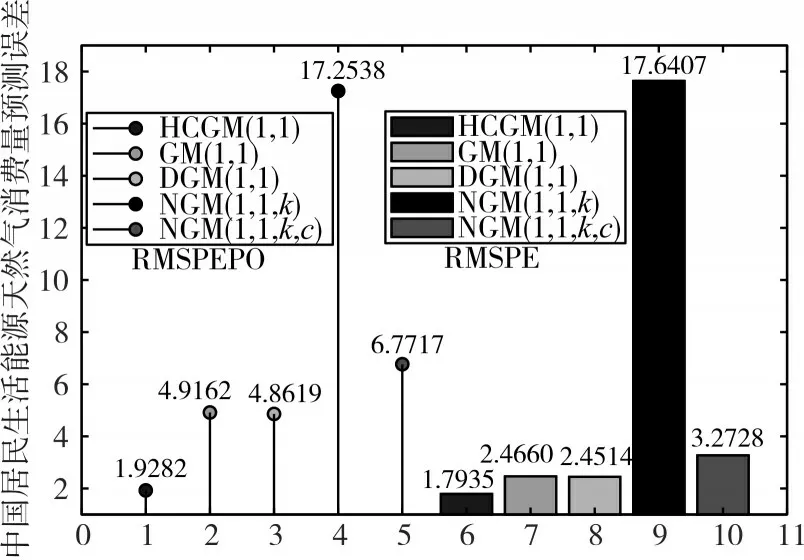
图4 天然气消费量不同模型的预测误差

表2 中国居民生活能源天然气消费量不同模型的预测值

1）HCGM（1，1）模型的预测和总体均方根百分比误差均最低，而GM（1，1，k）模型的建模均方根百分比误差最低，HCGM（1，1）模型具有很好的预测能力，而NGM（1，1，k）模型的预测、总体误差最大；

2）所有模型建模计算结果均在真实数据左右浮动，所有模型的预测值均低于真实值，而HCGM（1，1）模型的预测值最接近真实数据。

3.3 电力

选取2010 年～2018 年我国居民生活能源电力消费量为样本数据，其中2010年～2016年数据用于建立预测模型，2017 年和2018 年数据用于测试。五个预测模型求得的预测值以及均方根百分比误差值如表3 所示，模型预测结果比较及均方根百分比误差比较分别如图5、图6所示。

从表3、图5和图6可以看出：

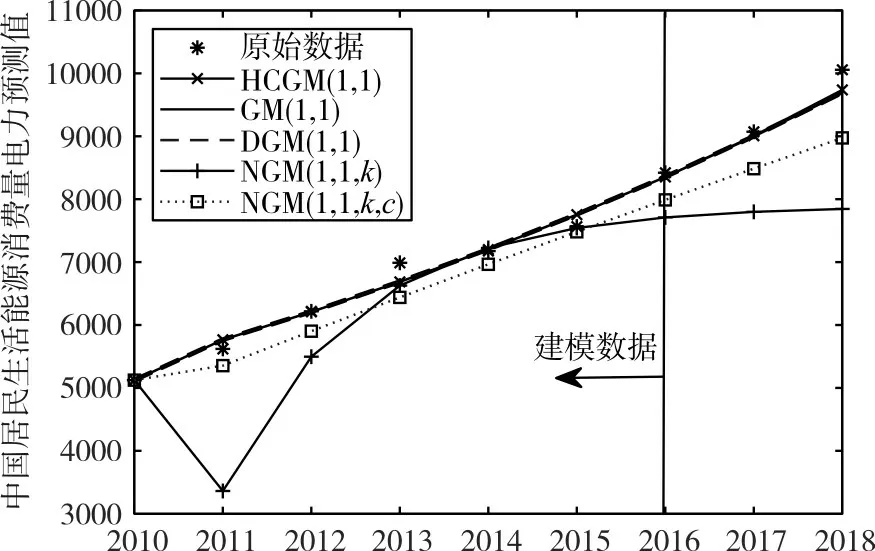
图5 电力消费量不同模型的预测图

图6 电力消费量不同模型的预测误差

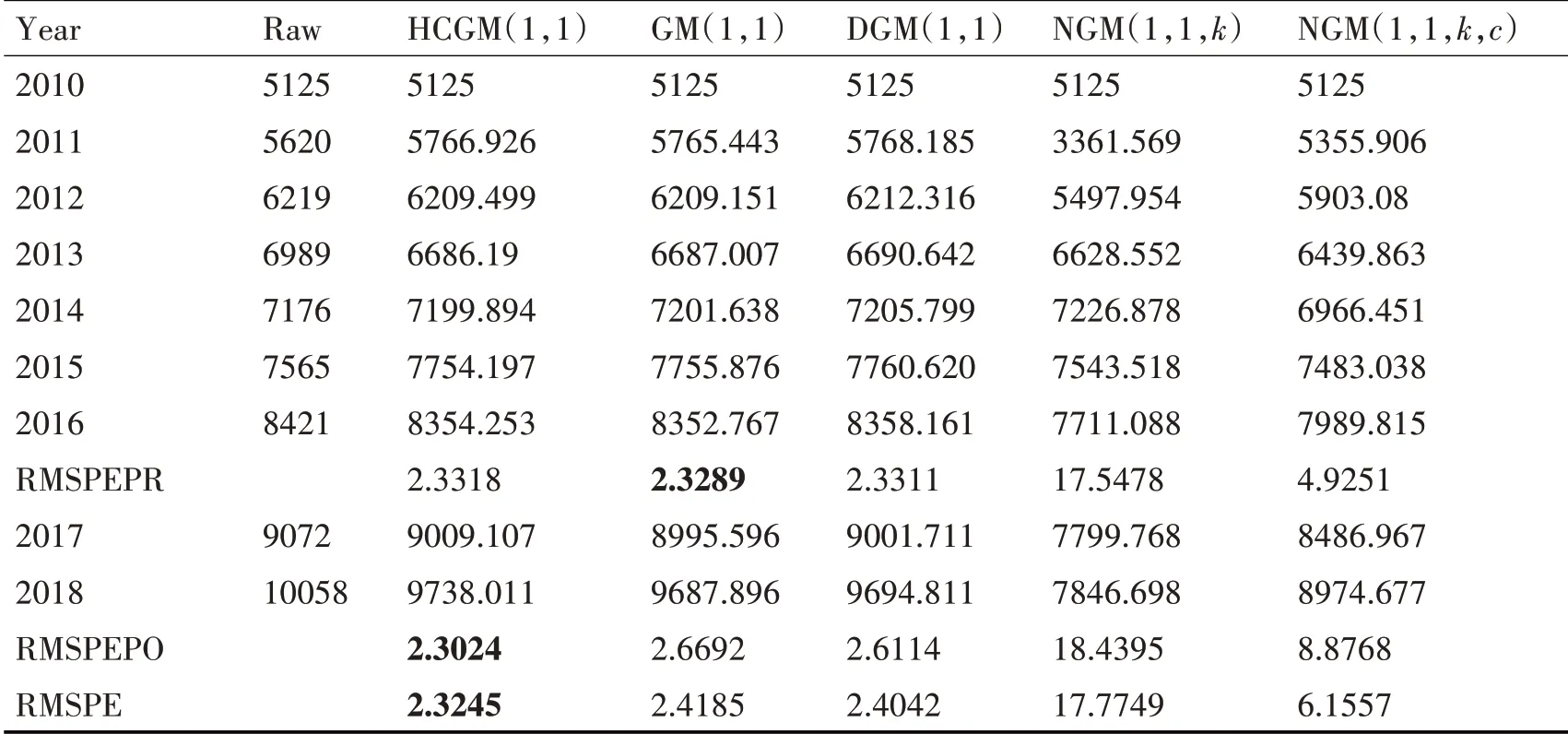
表3 中国居民生活能源消费量电力不同模型的预测值

1）HCGM（1，1）模型的预测和总体均方根百分比误差均最低，而GM（1，1，k）模型的建模均方根百分比误差最低，NGM（1，1，k）模型的建模、预测、总体的均方根百分比误差均最大，可见HCGM（1，1）模型具有很好的预测能力；

2）所有模型建模计算结果均在真实数据左右浮动，所有模型的预测值均低于真实值，而HCGM（1，1）模型的预测值最接近真实数据。

3.4 模型评价及应用

由GM（1，1）、DGM（1，1）、NGM（1，1，k）、NGM（1，1，k，c）以及HCGM（1，1）模型对我国居民生活能源热力、天然气和电力消费量的预测结果可以看出，HCGM（1，1）模型的预测、总体均方根百分比误差均最低，即其预测精度均高于其他四个模型，显示较好的预测能力。

选取2006年至2018年中国统计年鉴中居民生活能源消费量为样本数据，运用新型灰色预测模型HCGM（1，1）预测接下来3年热力、天然气和电力消费量，消费量预测结果及消费量年增长率分别如表4所示。由表4可见，我国居民生活热力、天然气和电力能源消费量总体呈上升趋势，天然气和电力增长平缓，但热力消费量增长迅速。十九大以来我国一直提倡能源产业低碳、绿色、健康、可持续发展的战略，建议加大力度发展水电、风电、太阳能发电，加强开发优品质天然气，一方面满足我国居民生产、生活能源需求，一方面有利于构建清洁低碳、安全高效的能源体系。

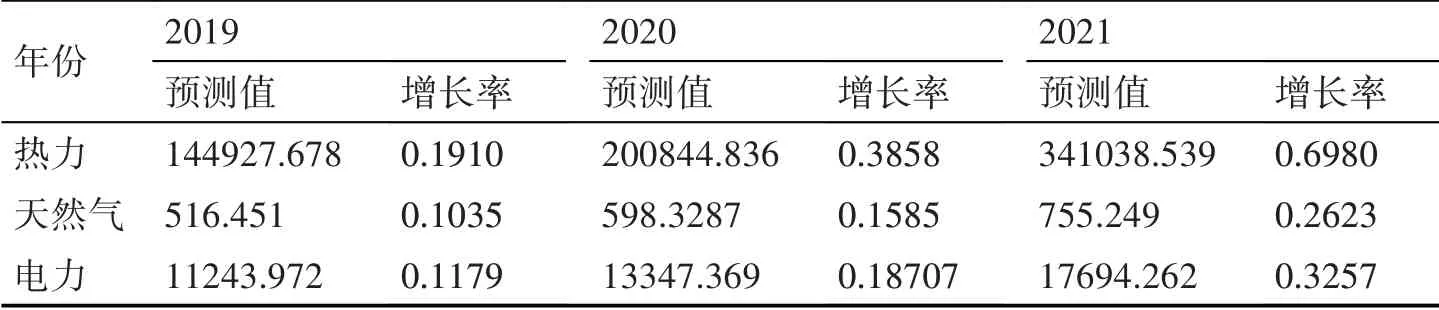
表4 HCGM（1，1）模型中国居民生活能源消费量预测值及增长率

4 结语

本文应用灰色建模技术和参数优化方法提出了新灰色模型HCGM（1，1），首先通过求解一阶非齐次白化微分方程的通解得到模型时间响应函数，其次通过对白化微分方程离散积分并结合两点梯形公式得到优化后的模型参数向量矩阵形式，最后运用线性最小二乘法计算参数向量值。以我国居民生活能源热力和天然气为样本，使用HCGM（1，1）模型等五种模型进行仿真，并预测了近三年能源消费量及发展趋势，但由于缺乏近三年相关数据从而无法进一步确定其准确性。仿真结果表明新灰色模型HCGM（1，1）对于短期热力消费量预测结果较准确性，但2019 年底以来爆发的全球新冠肺炎疫情给全球经济及能源系统引发的巨大改变，可能使得近三年预测与真实数据可能存在较大的误差。