基于EMD-LSTM 的船舶运动姿态短期预测*
2022-08-26夏骏达郑伟伦王子涵
夏骏达 郑伟伦 王子涵 李 军
(南京理工大学 南京 210094)
1 引言
随着经济的发展,我国的海洋活动日益增多,例如远洋运输、海上风电运维以及科考研究等。船舶在海上作业时,受海风和海浪的影响会产生横摇、纵摇、偏航、横荡、纵荡和升沉六个自由度的运动,这些运动严重影响了船舶上的正常活动[1]。尤其是在海域状况恶劣的情况下,由于船舶姿态的快速变化,将导致波浪补偿系统不能很好地保持稳定,海上作业活动不能正常展开。因此,进行船舶运动姿态预测就显得尤为重要,能够有效提高波浪补偿系统的滞后性,从而提高在大风浪中作业的安全性[2]。
目前,比较常用的方法是利用时间序列分析的方法对船舶建模,从而实现船舶运动姿态预测[3]。在时间序列分析方法中,比较经典的模型有自回归模型(AR)[4]。目前,该模型已经在多个领域得到应用,但是在面对复杂的非线性信号时仍存在问题。
在对非线性非平稳信号的处理时,神经网络方法的适应性和学习性都比较突出。常用的预测方法都是运用单一的预测模型完成时间序列建模工作,但是应对复杂的高海况时,预测精度还是有所欠缺。因此,本文采用了组合预测模型[5],能够有效结合各模型的优势,大大提高了预测结果的准确性。
王国栋[6]、黄礼敏[11]等采用AR、LSTM 模型对船舶横摇运动进行预测,但是发现上述模型在处理非线性非平稳数据时存在不足之处。针对信号的非平稳问题,对信号进行分解处理不失为一个好方法。比较常见的信号分解方法有傅里叶变换、经验模态分解和小波分析等方法。但是傅里叶变换不能从非平稳信号中提取频率信息,小波分析在低频信号检测及趋势检测方面表现不佳。考虑到经验模态分解对非平稳信号分析的适应性较强[7],本文提出了一种基于经验模态分解(EMD)的长短期记忆神经网络(LSTM)构成的船舶运动姿态预测模型,对数据的不同频域信息分别建模,而原始序列的预测结果为各分量预测结果的叠加。最后,对AR、LSTM、EMD-LSTM 三种模型的预测结果进行对比,结果证明本文方法有效。
2 舰船运动姿态的时间序列分析
由于受海浪扰动力的船舶运动姿态存在一定的周期性和相关性,时间序列方法能够根据船舶运动姿态的历史序列值,对未来的数据进行预测。
下面以时间序列AR 模型为例[8],假设以采集的时间序列为{xt},AR模型的一般形式为
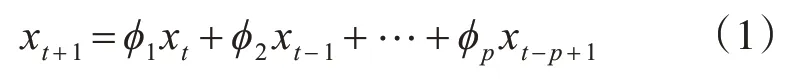
式中:p为自回归模型的阶数;ϕ1,ϕ2,…,ϕp为自回归系数,这种模型记为AR(p)。
式(1)是AR模型提前预测一步的模型,如需要提前预测L步,公式为
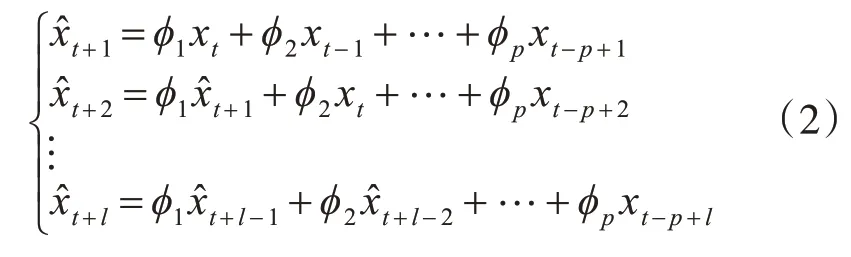
时间序列AR 模型算法,主要包括模型的系数估计、确定模型定阶以及序列值预测三部分。该模型最主要的是要确定自回归系数和模型阶数,这一部分计算较为复杂,操作繁琐,需要消耗不少时间,且若系数和阶数选择不够准确的话,会对预测结果造成比较大的影响[9]。
3 基于EMD-LSTM的组合模型
3.1 经验模态分解
经验模态分解(Empirical Mode Decomposition,EMD)是一种新的信号分解方法,相较于常用的信号分解方法,如傅里叶变换、小波分析、频谱分析等[10],EMD 完全抛开了基函数的束缚,且几乎能将任何类型的信号进行分解。该算法的核心思想是,将复杂的原始数据分解成有限个本征模函数(IMF)和残差信号,这些IMF 分量具有原始数据在相应时间尺度上的所有波动信息[11]。
设定原始数据样本数据为x(t),分解步骤如下:
1)初始化:r0=x(t),i=1。
2)得到第I个IMF。
(1)初始化:h0=ri-1(t),j=1;
(2)找到原始数据hj-1的局部最大值和最小值。根据局部极值拟合出上下包络曲线xmax(t)和xmin(t),并求得包络线的平均值序列mj-1(t):
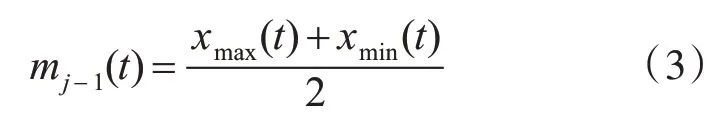
(3)原始信号与包络线平均值之差即为疑似IMF分量hj(t) :
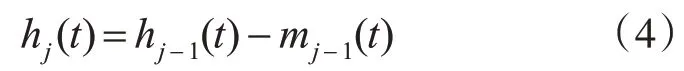
(4)随后判断疑似IMF 分量hj(t)是否符合IMF分量的两个条件。若hj(t)满足IMF 分量的两个条件,那么该信号就是一个IMF 分量;如果不满足其中一个条件,就以该信号作为基础,重新进行步骤(2)~(4)的分析,且需要j=j+1。一般情况,IMF 分量的获取需要若干次的迭代才能完成。
3)通过步骤1)、2)得到IMF1后,用原始信号减去IMF1作为新信号。
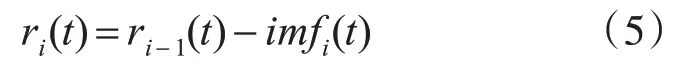
4)如果ri(t)极值点数仍多于两个,则i=i+1,并且将ri(t)作为一个新信号,再通过步骤2)的分析;否则,分解结束,将ri(t)作为残余分量。算法最后可得:

3.2 EMD-LSTM算法
由于船舶运动姿态信号是非线性非平稳信号,直接对其进行预测会影响预测精度。采用EMD 方法对非平稳数据进行平稳化处理,能够将复杂信号分解成为一组性能较好的本征模函数和残差信号。所分解出来的IMF 分量中包含了原始信号的不同时间尺度的局部特征信号,且EMD 方法完全抛开了基函数的束缚,对各种信号都有较好的兼容性。LSTM 模型由于自身内部结构的特点,能够实现对依赖信息的长时间学习。因此,本文结合两个算法的优势,采用组合预测模型进行船舶运动姿态的预测[12~13]。
图1 为EMD-LSTM 船舶运动姿态预测模型流程图,步骤如下:

图1 EMD-LSTM组合模型预测船舶运动姿态流程图
1)船舶运动姿态序列进行分解。通过EMD 方法能够将原始信号分解为有限个本征模函数{IMF1,IMF2…,IMFn}和残差信号rn。
2)LSTM 模型通过训练学习各IMF分量和残差信号的短期时序规律,对各个LSTM 模型进行参数调整,从而使预测精度更高。各IMF分量和残差信号分别通过对应的LSTM 进行时序预测,并将各分量预测出的信号进行叠加得到预测值。
3)将组合模型的预测结果与实际数据进行对比分析,求出平均绝对百分比误差(MAPE)和均方根误差(RMSE)作为预测误差的指标。
4 仿真结果与分析
4.1 仿真条件
本实验选取船舶横摇作为示例,船舶运动姿态的数据是通过Mti-300 系列传感器在盐城港采集得到。EMD-LSTM 组合预测模型选取10s 内的1000 个样本值,其中训练样本与预测样本的数量分别设置为800和200。
4.2 EMD分解
以横摇为例,将船舶横摇数据按照EMD 分解流程进行分解,获得3 个本征模函数和一个残差分量。其中,IMF1频率最高,代表的是横摇信号中的高频成分;res是最低频的信号,代表的是横摇信号中非线性趋势项。图2 为横摇原始数据及EMD分解后的各分量。
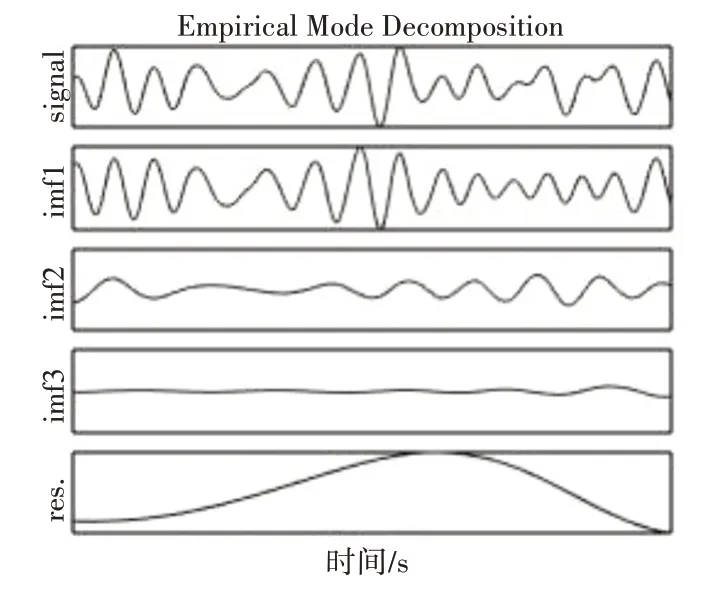
图2 横摇原始数据及EMD分解情况
4.3 仿真结果误差统计
本文将采用平均绝对百分比误差(Mean Abslute Percentage Errors,MAPE)和均方根误差(Root Mean Square Error,RMSE)这两个指标作为本课题的统计预测误差方法。指标的计算公式如下:
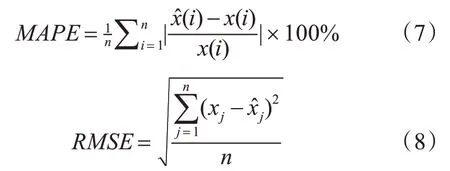
通过分析图3~5 及由表1 可知,在预测横摇角的实验中,EMD-LSTM 组合模型相对于AR 模型和LSTM 模型,在MAPE 上分别降低了18.34%、4.09%,在RMSE 上分别降低了0.4175°和0.0633°。结果表明,EMD-LSTM 组合模型方法相较于LSTM模型方法和AR模型方法有更好的预测精度。
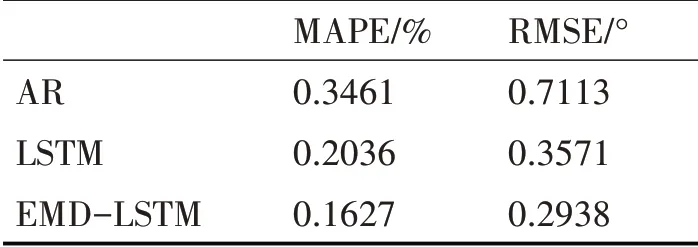
表1 横摇角误差统计
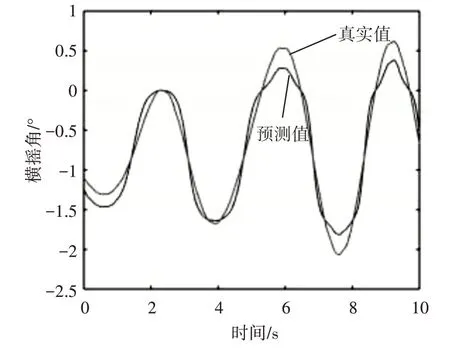
图3 AR模型方法预测结果
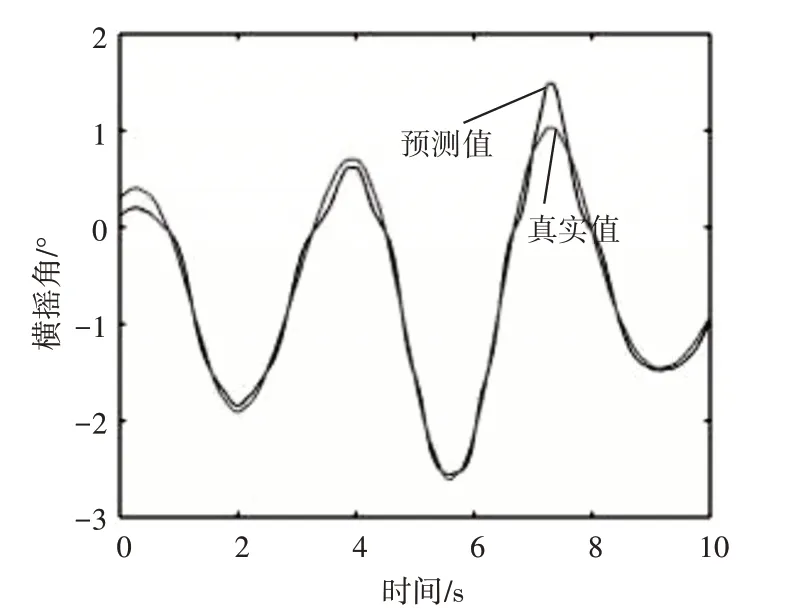
图4 LSTM模型方法预测结果
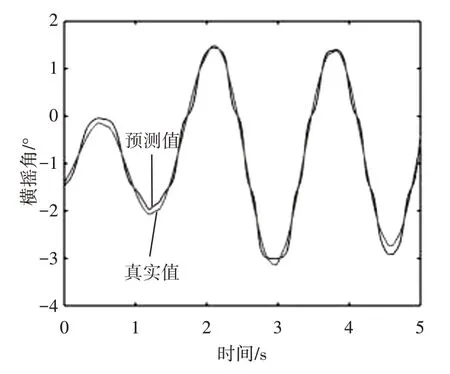
图5 EMD-LSTM组合模型方法预测结果
5 结语
船舶在海上作业时,由于船舶周围海域环境的随机性姿态,造成了船舶运动姿态的复杂性和不确定性。为了能够准确预测船舶运动姿态,提高波浪补偿系统的控制精度,保障海上作业的安全性。本文提出了基于EMD-LSTM 的船舶运动姿态预测模型,通过EMD 方法将非线性非平稳的船舶运动姿态信号数据分解成若干个本征模函数和残差信号的组合,然后对不同特征的信号分别进行LSTM 建模预测,最后将各个预测分量叠加起来,得到最终的预测结果。同时将该预测模型的结果与AR模型和LSTM 模型的预测结果进行对比。通过实际数据验证表明,基于EMD-LSTM 的非线性非平稳船舶运动姿态信号预测模型的精确度更高。
在接下来的工作中,需要结合可能的应用场景,如稳定平台安全作业等,对该组合预测模型进行进一步的调整、优化,以期得到更好的预测结果与应用。
