季节模型在某医院月门诊量预测中的研究与应用

李卫霞+高蕾+王媛媛

摘要：根据海南省某医院月门诊量时间序列的特征，首先识别出多个可能的季节模型，经模型检验对比后构建了最优的乘积季节模型；然后利用季节模型分析了该医院月门诊量的周期性及趋势性变化规律；最后基于最优模型对该医院月门诊量进行预测，进而验证了月门诊量变化规律符合生活实际情况，建立的最优季节模型具有科学性及可行性，季节模型分析的预测值为医院门诊管理工作提供参考建议。

关键词：月门诊量；时间序列；季节模型；预测值

Abstract：According to the features of outpatient numbers time series for one hospital in Hainan province， firstly identify several possible seasonal models， and construct the best multiplicative seasonal model by using models testing and comparison； then analysis change regularity of the periodicity and trend by the seasonal model ； finally forecast the outpatient numbers of that hospital based on the best model which has been given， and verify that change regularity conform to the reality of life. The best seasonal time series model which had been constructed had the scientific nature and feasibility， thus， the predictions of the model give recommendations for the hospital outpatient management.

Key words：Monthly outpatient number ；Time series；Seasonal model； Predictive value

隨着海南国际旅游岛建设的不断加快，人口数量也在不断加大，经济在发展和人们生活水平在提高，这将对卫生产品和医疗服务供给的需求加大，提高医疗服务水平对于海南省建设至关重要。门诊量[1]是评价一个医院医疗工作的重要指标之一，直接或间接地反映出一个医院的规模、医疗质量及医术水平，一个医院的医疗水平及服务直接地影响人们的就医选择。从而，门诊量的科学分析及预测至关重要，为科学管理门诊工作的有力依据。一元时间序列分析是一种考虑对象本身的历史数据随时间发展变化的规律，即其不需考虑影响预测变量的相关因素，该法用于医院管理相关指标预测的优点突出，季节模型是一种特殊的考虑季节性效应的时间序列分析模型，其可对时间序列的趋势性及季节性综合分析，已有很多卫生工作者将该法应用于医院管理、疾病控制等领域[2-4]，在前瞻性预测方面有较高的应用价值。

1 预备知识

1.1数据来源 海南省某医院提供的信息系统数据，数据内容为该医院2009年1月～2014年12月每月的月门诊量，数据连续，来源真实可靠。

1.2 ARIMA（p，d，q）×（P，D，Q）S模型

称（1）式为乘积季节性模型[5-7]ARIMA（P，D，Q） × （p，d，q）s，P，D，Q分别表示自回归阶数、差分阶数和移动平均阶数，p，d，q分别表示季节性自回归、差分和移动平均的阶数，s表示周期长度。

1.3建模方法与步骤 建模基本步骤[8]如下。

步骤1：判断平稳性及平稳化；步骤2：模型定阶。根据样本自相关系数和偏自相关系数的性质，选择阶数适当的ARIMA（P，D，Q） × （p，d，q）s 模型进行拟合；步骤3：估计模型参数；步骤4：检验模型的有效性。如果拟合模型检验不通过，转向步骤2，重新选择模型再拟合；步骤5：模型优化。如果拟合模型通过检验，仍然转向步骤2，充分考虑各种可能，建立多个拟合模型，从所有通过检验的拟合模型中选择最优模型；步骤6：利用拟合模型，预测序列的将来走势。

2建立季节模型

以下应用Eviews6.0软件省某医院2009年1月～2014年12月的月门诊人数为原始数据时间序列，命名为M。建立季节模型，对模型诊断及动态预测。

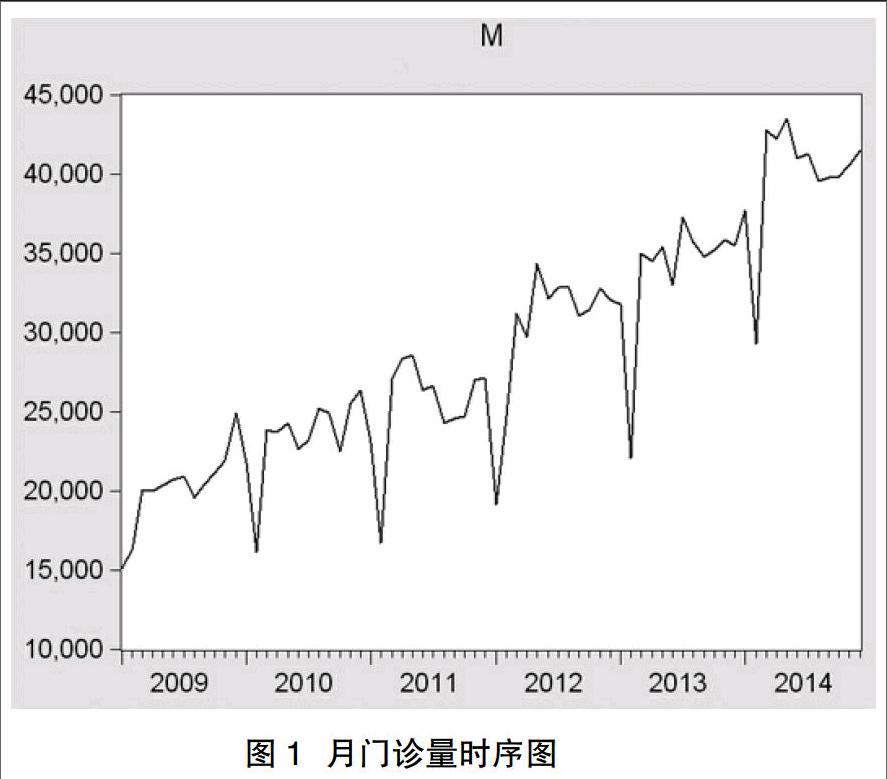
2.1平稳性检验 对序列{M}做时序图，如图1所示。

由时序图可以看出月门诊人数除了有不断增长的趋势外，又存在周期性，直观上初步判断序列为非平稳序列。对序列进行单位根检验，进一步准确判断序列平稳性，采用ADF检验[8]结果表1所示。

ADF的检验统计量为1.895540小于对应显著性水平0.05对应的临界值-2.910860的绝对值，从而不拒绝H0，说明该时间序列存在单位根，数据不平稳。

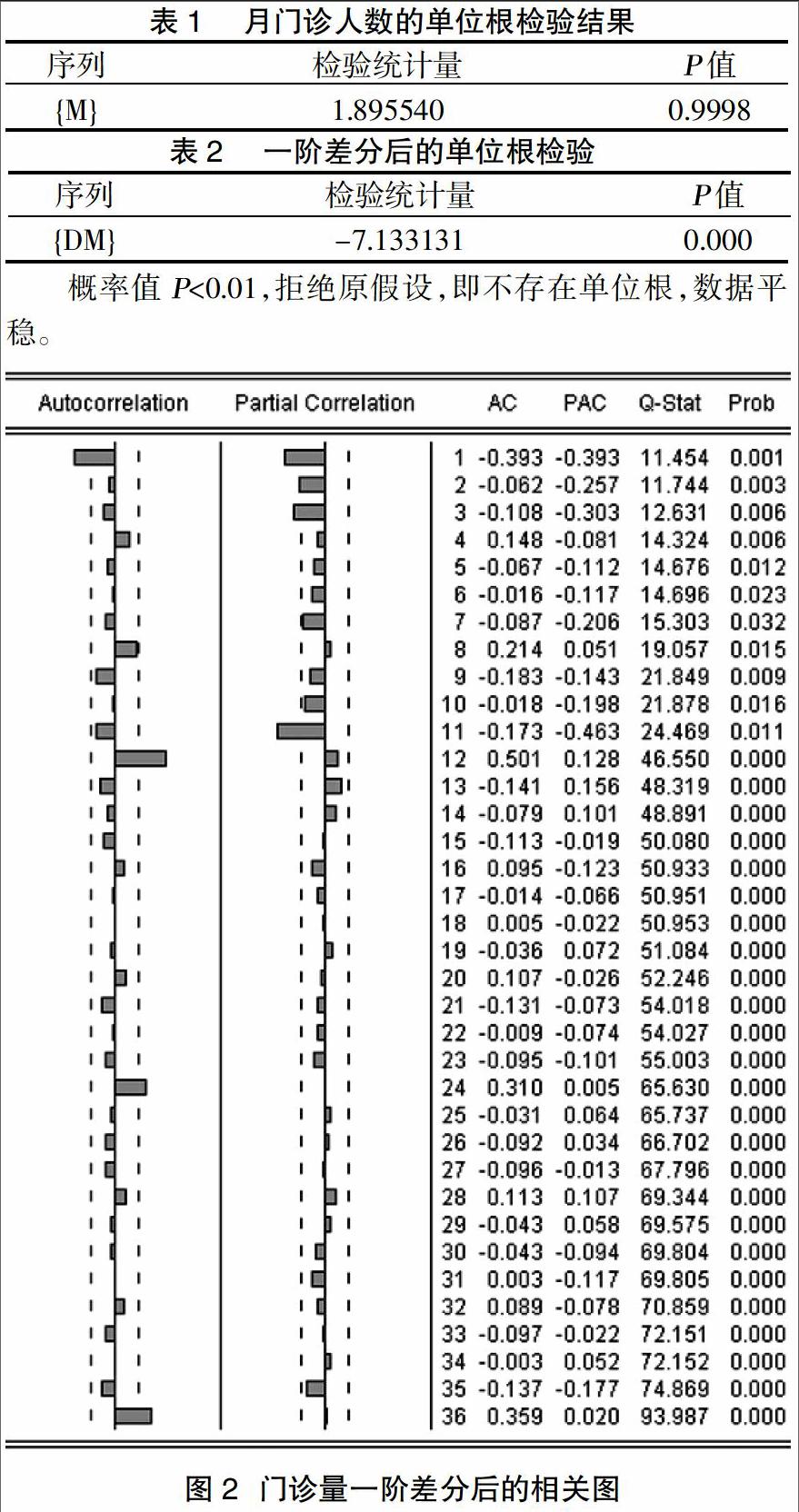
3.2序列平稳化 消除门诊量序列的长期增长趋势，进行平稳化处理，对数据进行一阶差分，差分序列命名为"DM"，对序列{DM}进行单位根检验结果表2所示。

概率值P<0.01，拒绝原假设，即不存在单位根，数据平稳。

一阶差分后的相关图（图2）所示。当滞后期K=12，24，36时，序列的自相关系数与零有显著性差异。这表明月门诊量具有以12为周期的季节性波动，为消除月门诊量的季节性，再进行步长为12的一阶季节差分，得到新序列命名为"M12"，其相关图如图3所示。

2.3模型定阶与识别 对序列进行一阶季节差分消除了长期趋势和非稳定的季节变动成分（图3），AC显示该时间序列可能适应季节性MA模型，AC非季节部分（P=1）1阶截尾且PAC非季节部分2阶（Q=2）截尾，AC季节部分在K=12期（p=12）时与零显著，但在K=24（p=24）时已经在2倍标准差之内，初步识别可能适应模型ARIMA （0，1，1）×（0，1，1）和模型ARIMA（2，1，0）×（0，1，1）12。

在不同模型参数检验通过的基础上，使AIC准则和BIC准则达到最小的阶数为理想阶数[9]如表3所示，综合比较最终通过检验的理想模型是ARIMA（2，1，0）×（0，1，1）12。

2.5模型检验 参数估计后，对模型残差序列进行白噪声检验[10]。对残差进行纯随机性检验（图4），由自（偏）相关函数值均在2倍标准差之内，P值均>0.05（α=0.05），模型的残差序列不存在自相关，为白噪声序列，模型适应性检验通过。

2.6预测 两种通过检验的模型模型ARIMA（2，1，0）×（0，1，1）12及ARIMA（0，1，1）×（0，1，1）12分别对原始数据进行动态预测，将两个模型的2014年1月～12月预测值与真实值做线图对比（图5）。其中，MF1是模型ARIMA（2，1，0）×（0，1，1）12的预测值曲线，MF2是模型ARIMA（0，1，1）×（0，1，1）12的预测值曲线。模型预测值与原始的数据趋势误差小，呈上升趋势，周期性的拐点变化时间也基本相同。图5显示MF1比MF2与真实值更贴近，故前者的预测误差比后者小。进而利用最优的模型ARIMA（2，1，0）×（0，1，1）12对2015年1月～12月的医院月门诊量进行预测，见表5。

3 结论

本文建立了季节模型ARIMA（2，1，0）×（0，1，1）12。模型分析了月门诊量具有逐年上升的长期趋势和以12为周期的规律性变化。医院月门诊量在每年不同月份的人数规律变动，在1、2月普遍较低，一年一度的元旦、春节期间，人们大多不愿意就医；3、4月份天气变暖，细菌、病毒开始活跃，疾病发生随之增加，门诊量逐渐上升；海南5月～8月基本高气温持续，夏季较长，肠道疾病，中暑等疾病增加等原因，医院门诊量较高。在不同月份的门诊量变化，可能与人们的就医观念、节假期、气候变化等因素有关。医院可以根据季节变化规律合理安排门诊工作，调整各个科室人员配备。模型对门诊量的动态预测可作为医院管理层制定门诊工作计划的依据，统计模型预测已经逐渐成为一种不可缺少的工具[10]，科学、准确地分析医院月门诊量动态变化，预测趋势，对于合理安排人、财、物资源，提高经济效益和社会效益都有重要意义[11-14]。

参考文献：

[1]李海燕，张徐龙. 2000年～2009年门诊量变化趋势分析[J].中国病案 ，2011，06：60-61.

[2]陈莉. 探讨ARIMA模型在细菌性痢疾发病预测中的应用[J]. 中国卫生统计，2011，04：417-419.

[3]陈明惠，胡云，支洋英，等. 应用ARIMA模型预测成都市新都区麻疹的发病趋势[J]. 现代预防医學，2012，02：267-269.

[4]叶孟良，李智涛，欧荣. ARIMA模型在预测重庆市医院日住院量中的应用[J].重庆医学，2012，13：1260-1261.

[5]Bowerman，O'connell forecasting and time series：an applied （Third Edition） [M] .China Mchine Press，2003：117-156.

[6]王沁.时间序列分析及其应用[M].成都：西南交通大学出版社，2008.

[7]史代敏，谢小燕.应用时间序列分析[M].北京：高等教育出版社，2011.

[8]王燕.应用时间序列分析[M].北京：中国人民大学出版社，2012.

[9]刘晓宏，金丕焕，陈启明. ARIMA模型中时间序列平稳性的统计检验方法及应用[J]. 中国卫生统计，1998，03：14-16.

[10]Gorlov MI，Strogonov AV. ARIMA model used to predict the time to degradation failure of TTLICs[J]. Russ Microelect，2007，36（4）：261-270.

[11]向前，陈平雁. 预测医院门诊量的ARIMA模型构建及应用[J]. 南方医科大学学报，2009，05：1076-1078.

[12]冯丹，曹秀堂，董军，等. 综合性医院收容量预测的ARIMA模型构建研究[J]. 解放军医院管理杂志，2007，02：101-103.

[13]梁桂玲，刘颜，邓泗沐. ARIMA模型应用于月门诊量预测[J]. 中国医院统计，2006，01：24-26.

[14]周忠彬，吕红梅，邹郢. ARIMA干预模型在医院门诊量预测中的应用[J]. 中国医院统计，2008，02：110-112.编辑/蔡睿琳