基于IAO-MCKD的电机轴承故障诊断*

刘福康，杨光永，王 林，吴大飞，徐天奇

(云南民族大学电气信息工程学院，昆明 650000)

0 引言

针对电机轴承的故障研究，目前有短时傅里叶变换与小波分析[1]、最小熵反卷积[2]、变分模态分解[3]等。其中最小熵反卷积(MED)广泛应用于轴承的故障诊断[4]。但MED对周期信号存在一定缺陷，为了能有效提取周期性脉冲分量，抑制信号噪声的影响，McDonald等2012年在MED的基础上提出了最大相关峭度反卷积(MCKD)[5]。该方法以相关峭度值作为评价指标，提取有用信号从而达到降噪目的。目前，MCKD已在滚动轴上对旋转机械零件，如轴承[6]、齿轮[7]故障诊断时取得了显著成效。但MCKD参数的选择需要人工的设置，且参数的不同对算法的影响较大，为充分发挥MCKD算法的降噪性能，提取有效信号，文献[8]中采用粒子群算法实现了MCKD参数滤波器阶数L和周期T的自适应选择，但其方法收敛速度较慢，且容易陷入局部最优。

综上所述，使用MCKD对信号进行处理时，往往需要确定滤波器阶数L，周期T和位移数M等主要参数，针对以上情况，为了提高MCKD降噪效果，本文提出了一种新的方法：采用改进AO算法优化MCKD，通过构造适应度函数，对滤波器阶数L和周期T等参数实现自适应选择，从而解决了人工选择参数对MCKD算法所造成的影响，将改进后的AO算法与经典的天鹰算法[9]，粒子群算法[10]和麻雀算法[11]做了对比实验，实验证明，改进后的AO算法具有收敛速度更快，处理陷入局部最优问题更灵活等特点。

1 最大相关峭度反卷积

电机轴承故障信号可表达为：

y(k)=x(k)+en

(1)

式中，y(k)为传感器采集的观测信号；x(k)为轴冲击序列；en为噪声分量。

最大相关峭度反卷积(maximum correlated kurtosis deconvolution)算法的实质是利用相关峭度来提取脉冲序列，解决了峭度受单个或部分高阶脉冲的影响及无法全面考虑故障信号的周期性和连续性等问题。最大相关峭度可定义为：

(2)

式中，T为冲击信号周期；N为样本信号个数；M为位移数。

由式(2)可以看出相关峭度受周期T和滤波器阶数L的影响，为寻找最有滤波器f(n)，从而使原始信号x(n)的相关峭度最大，因此式(2)可以更新为：

(3)

式中，f=(f1,f2,f3,f4,...,fL)T；L为滤波器的阶数。

为确定最优滤波器f(n)，使得CKM(T)最大，式(3)求导得：

(4)

最终求得滤波器系数结果为：

(5)

式中：

滤波器阶数N和反卷积周期T是MCKD的两个重要参数，周期T的大小决定了MCKD能否提高故障频率。在处理不同信号时，由于信号的特性各不相同，参数的选择也并不固定，因此需要根据信号的特性确定MCKD的参数，周期T由采样频率和故障特征频率的比值确定即：

(6)

式中，fs为采样频率；fg为故障特征频率。

但实际问题中噪声信号往往是复杂多变的，周期T的值与理论值存有一定误差，且T和L互相影响，所以在使用MCKD算法对噪声信号进行处理时，周期T和滤波器阶数L的选择是信号处理结果的关键，参数选择的不同，导致信号处理的结果也大不相同。因此，为解决MCKD算法的局限性，T和L进行适应性选择的研究具有重要意义。

2 改进天鹰算法优化MCKD

2.1 天鹰优化算法

天鹰算法(aquila optimizer)是一种新的元启发式优化算法，该方法具有强大的搜索能力，收敛性强，处理问题灵活等特点。在AO中，优化规则从候选种群开始如式(7)所示，其侯选解在给定问题的上界(UB)和下界(LB)之间随机生成，在每次迭代中，最优解被确定为近似最优解。

(1)拓展探索：天鹰识别猎物区域，并通过高跃和垂直弯曲来选择最佳狩猎区域。其表达式为：

(7)

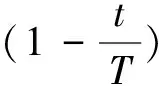
(2)缩小探索范围：当从高空发现猎物区域时，天鹰在目标猎物上方盘旋，准备着陆，然后攻击。其表达式为：

X2(t+1)=Xbest(t)×levy(D)+XR(t)+(y-x)*rand

(8)

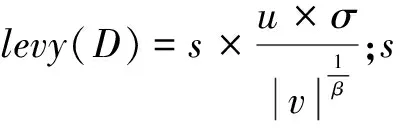
(9)

式中，β是一个固定为1.5的常量；Γ为标准的伽马函数。

(3)扩大开发：当猎物区域被精确捕捉时，天鹰准备着陆和攻击，垂直下降，进行初步攻击，观察猎物的反应。其表达式为：

X3(t+1)=(Xbest(t)-XM(t))×α-rand+((UB-LB)×rand+LB)×δ

(10)

式中，α和δ是开采调整参数，其值较小，在(0,1)的范围内。

(4)缩小开发范围：当天鹰接近猎物时，天鹰根据自己的随机运动在陆地上空攻击猎物。其表达式为：

X4(t+1)=QF×Xbest(t)-(G1×X(t)×rand)-G2×levy(D)+rand×G1

(11)

(12)

式中，QF(t)是迭代时的函数值。

2.2 Tent混沌映射

在天鹰初始化种群的过程中，由于是采取的是随机分布，所以会使初始种群个体分布不均匀，容易导致算法陷入局部最优，降低算法的全局搜索能力，而混沌变量则具有随机性，遍历性和规律性等特点[12]，且Tent映射比Logistic映射遍历均匀，寻优效果更好，Tent映射具有严格的数学推导过程，所以采用Tent映射作为天鹰算法的混沌序列。

Tent映射的表达式为：

(13)

Tent映射经过伯努利移位变换后其表达式为：

xi+1=(2xi)mod1

(14)

2.3 IAO-MCKD诊断流程

本文将滤波器阶数L和周期T作为待优化参数，以最大峭度作为适应度函数，假设天鹰在一个二维空间内进行搜索，判断猎物的情况，通过迭代不断更新个体位置，将AO算法引入Tent混沌搜索后，增强了算法的搜索能力，可以有效避免其陷入局部最优，从而以较快的速度和稳定性搜索到目标参数。

图1 基于IAO-MCKD诊断流程图

首先，初始化种群并引入混沌映射，确定待优化参数的上下界，并对参数[L,T]的取值进行寻优，寻找到最佳的线性组合[L0,T0]；然后，对获取的样本进行降噪处理；最后，对信号进行解调，诊断故障类型，确定故障部位。

3 实例分析

为验证本文方法的有效性，以机械故障预防技术学会(MFPT)的轴承故障数据集进行试验并验证。

表1 轴承结构参数

在该轴承中输入轴速率为25 Hz，采样速率48 828，持续时间sps=3 s，根据表1的轴承结构参数，计算出内圈故障频率fi和外圈故障频率fo分别为81.13 Hz和118.7 Hz。

图2 NICE实验原理平台

图2为实验台原理，实验台中的传感器可以采集多种类型的原始数据，包括转速振动数据，位移振动数据，加速度数据，传感器收集的原始数据存储于数据采集箱，为了模拟轴承的不同故障，实验采用电刻度方法分别在实验轴承的内圈和外圈刻出划痕来模拟故障特征，所采集试验信号的内圈和外圈的时域波形和频谱图，分别如图3和图4所示， 从图中可以看出时域信号由于受到较强噪声的干扰几乎无法观测出任何冲击成分，频谱图也无法分析出故障脉冲信号成分。面对此情况便无法分析出故障特征，本文采用改进AO算法对MCKD算法中的两个参数：滤波器阶数和周期进行寻优,输出得到最佳线性组合后，再对信号进行降噪处理，得到信号故障特征。

图3 内圈故障信号及频谱图 图4 外圈故障信号及频谱图

3.1 内圈故障诊断

通过改进后的AO算法对MCKD算法参数进行寻优后，得到最佳线性组合[L0,T0]，将滤波器阶数设置为L=399，周期设置为T=91，通过参数优化后MCKD算法处理后的信号结果如图5所示，从时域信号可以看出内圈信号经过参数优化后的MCKD降噪处理，去噪效果以及故障冲击成分都更加明显，通过图6对信号进行包络谱分析可以分析得出f1≈fi，且可以基本分析出f1～f6甚至更多的频率成分。

图5 内圈故障处理后信号 图6 内圈故障处理后信号包络谱

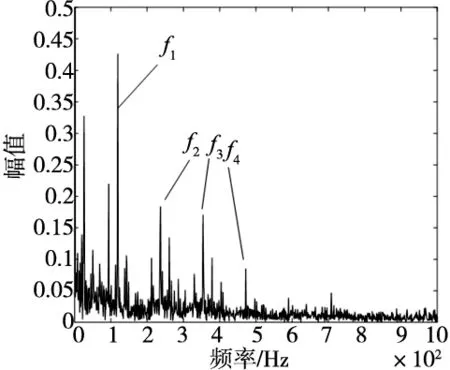
图7 随机参数处理的内圈信号包络谱

为验证IAO-MCKD方法对轴承内圈故障提取的有效性，将滤波器阶数和周期的线性组合设置为L1=245；T1=104，处理后的信号包络谱如图7所示，图中只能分析出f1～f4，无法分析出更多的倍频成分。

3.2 外圈故障诊断

图8 外圈故障处理后信号

采用如3.1节相同的方法，对轴承外圈故障信号进行分析，通过改进后的AO算法对MCKD算法参数进行寻优后，将滤波器阶数设置为L=398，周期设置为T=214，处理后的信号结果图如图8所示。

可以明显看出通过优化后的MCKD算法，对故障信号进行处理后，冲成分更突出，如图9所示外圈故障信号处理后的频谱图中故障特征频率f0及其倍频的谱线清晰可见。

同样，为验证IAO-MCKD方法对轴承外圈故障信号提取的有效性，将滤波器阶数和周期的线性组合设置为L1=298；T1=114，处理后的信号包络谱如图10所示。

图9 外圈故障处理后信号 图10 随机参数处理的外圈信号包络谱

图中无法分析出有效的故障频率成分。从而验证了所提出的IAO-MCKD方法对轴承故障提取的优越性以及有效性。

3.3 实验对比

将IAO-MCKD方法与现有的基于PSO优化MCKD和SSA优化MCKD分别进行内圈寻优迭代次数和外圈寻优迭代次数对比，如图11和图12所示。

图11 内圈寻优对比结果图 图12 外圈寻优对比结果图

可以看出无论是内圈还是外圈寻优，AO算法都表现出了强大的搜索能力和其最优特性。在寻找最优参数时，AO算法通过跳出局部最优达到全局最优，收敛速度明显比PSO算法和SSA算法要快，AO算法经过Tent混沌映射改进后，初始个体位置更均匀，增强了算法的搜索能力，在面对陷入局部最优解问题时，IAO算法表现的比AO算法、PSO算法和SSA算法更灵活。

4 结束语

在面对噪声干扰时，通过合理设置天鹰算法的目标参数及适应度函数来优化MCKD中滤波器阶数和周期等参数，可以有效解决无法提取被强噪声干扰的故障冲击信号，并且规避了人为选择参数可能造成的影响，从而有效提取轴承内圈、外圈的故障信号周期频率成分。

通过实验分析，IAO算法具有强大的搜索能力且收敛速度快，面对陷入局部最优解问题时，IAO算法表现更灵活，可以有效避免陷入局部最优，从而证明了IAO-MCKD方法在诊断被强噪声掩盖的故障信号方面的优越性与必要性。