基于粒子群的转子在线动平衡质量补偿优化*
2022-08-25石志新刘振鹏
王 展,石志新,张 珂,刘振鹏,张 博
(沈阳建筑大学机械工程学院,沈阳 110168)
0 引言
随着高端旋转机械朝着智能化、高精密化、高速化的方向发展,对其核心转子单元的工作性能要求也逐渐提高。而由于旋转部件在加工制造误差、安装工艺误差以及在正常运行中不可避免收到的磨损、冲击、高负载会导致转子出现质量不均匀的情况,造成转子不平衡故障,从而使得转子及其部件在运行过程中发生振动,因不平衡所引起的振动会大大影响旋转设备的运行精度甚至会运行故障及部件损坏[1],在线动平衡是实现不平衡故障诊断自愈的有效手段,其主要依靠动平衡装置对转子实时质量补偿来完成动平衡,因此动平衡质量补偿的精度和效率对旋转机械在线不平衡故障自愈性能起到至关重要的作用[2-3]。
实施动平衡的核心在于能高效高精度地完成质量补偿,而怎么样能够更准确地计算动平衡补偿量并且更快速地完成调控是提高动平衡精度和效率的关键点。近些年,针对在线动平衡调控方法及质量补偿策略方面的研究正成为国内外学术界的研究热点。针对轴系动平衡问题,以降低轴系的振动为目标,提出相应的动平衡方法,建立多转子串联轴系有限元模型进行验证,实现了既定目标[4-7]。为了解决航空发动机转子系统的动平衡问题,国内外学者通过在现有动平衡方法的基础上不断优化或改进相应的动平衡方法,建立相应的模型进行仿真验证[8-9]。在电主轴系统中考虑电磁力的影响,在平衡方程中加上气隙这一因素,提出了一种基于自动对中控制和磁控制力等效的刚性转子动平衡方法并利用实验验证了此方法的正确性[10-11]。针对现有动平衡方法的改进,提出了一种影响系数法的改进方法,把不平衡信息进行分解,得到了良好的平衡效果,为了进一步提高影响系数法的动平衡精度,建立了一种改进影响系数标定模型,结果表明平衡的结果在精度和效率上都有很大的提高[12-13]。将不同动平衡方法相结合,并应用于解决转子系统动平衡问题,在三维全息分解技术的基础上提出一种在全息动平衡中有效的添加试重的方法,利用影响系数法和全息动平衡方法相结合也可以有效降低转子系统的不平衡振动[14-15]。综上所述,国内外学者的研究主要针对转子动平衡不同方法以及关于不同工况不同转子的动平衡调控机理开展了多方面的深入研究,但目前针对在线动平衡过程中的质量补偿策略问题研究尚少,仍是现阶段在线动平衡研究领域的关键性问题。
转子在线动平衡的关键是平衡的精度和平衡的效率,而进一步提高在线动平衡的精度和效率是至关重要的。因此在动平衡力学机理及现有动平衡调控方法基础上,本文通过建立转子在线动平衡质量补偿策略优化模型,采用基于粒子群优化动平衡质量补偿的移动策略方案计算动平衡最优配重相位,实现更高精度和效率在线动平衡的目的。
1 转子在线动平衡机理
在线动平衡装置通过2个可以转动的配重块来平衡转轴的不平衡量,设置有传感器用来实时监测转轴的不平衡振动量,当监测到的振动量小于初始设置的电主轴的振动可允许的最小值时,可以认为转子系统达到了平衡状态。图1为转子动平衡头的平衡原理简图,可以更直观的表现动平衡头的平衡原理。图中的A、B小球代表动平衡头的2个质量块,C小球代表转轴的不平衡量。当主轴平衡时,可以得到:
F=F1+F2+η
(1)
F1=m1ω2r1
(2)
F2=m2ω2r2
(3)
式中,F为转轴的不平衡量;F1为质量块A产生的校正量;F2为质量块B产生的校正量;η为电主轴平衡后的残余不平衡力;m1为质量块A的重量;m2为质量块B的重量;ω为转轴的转速。
2 基于粒子群的动平衡质量补偿优化方法
2.1 优化模型建立
在对转子系统进行平衡时,它的残余不平衡力与主轴的不平衡力以及动平衡头产生的校正量之间的关系为:
η=(F1+F2)×F
(4)
式中,η为转子系统平衡后的残余力;F1为质量块A产生的校正量;F2为配重块B产生的校正量;F为主轴的不平衡力。
根据式(4),可以得到以下关系:
|η|=|(F1+F2)||F|sinσ
(5)
式中,σ为动平衡头质量块A和B产生的合力与电主轴不平衡力之间的夹角。根据平衡原理,将两个质量块移动的角度φA和φB为优化变量,转子系统的残余不平衡力为优化目标。数学模型为:

(6)
式中,α和β表示动平衡头中的质量块A和B在平衡头中的初始角度;φA和φB表示质量块A和B在的移动角度值;F1为质量块A产生的校正量;F2为配重块B产生的校正量;γ为转子系统的不平衡力的角度;F表示转子系统的不平衡力。
2.2 模型求解

图2 求解流程图
粒子群算法的每个配重块在N维空间内所在的位置都可代表其重量,可以当做一个可行解,配重块在N维空间内的飞行过程即为搜索过程。配重块通过不断改变飞行速度,进而位置不断改变,直到满足迭代条件或得到全局最优解。其具体算法的流程如图2所示。
随机生成N组(φA,φB)初始解作为粒子群算法的初始种群,然后随机生成2个随机数作为配重块质量的飞行速度以及距离。计算第m次迭代时的第j组初始解所对应的f(φA,φB)j,m,并根据f(φA,φB)j,m的大小进行选择淘汰,其中j满足j=1,2,3,…,N,m满足m=1,2,3,…,H,H为预设迭代次数。若达到最大的迭代次数,或者f(φA,φB)j,m的大小小于电主轴可允许的最大的振动值,将会输出结果。
若f(φA,φB)j,m的大小大于转子系统可允许的最大的振动值,则会进行下一轮迭代。根据设置的初始飞行速度以及距离更新配重块质量,并改变配重质量的下一次的飞行速度以及距离。配重块的速度V和位置X通过下式进行改变:
Vid=ωVid+C1random(0,1)(pid-Xid)+C2random(0,1)(pgd-Xid)Xid=Xid+Vid
(7)
式中,ω为惯性因子,其值恒小于0;C1为个体学习因子;C2为种群学习因子,C1、C2均为常数,通常C1=C2=2;random(0,1)为[0,1]上的随机数;pid为每个粒子在N维空间的最优位置;pgd为全局最优位置。
3 实验验证
3.1 搭建实验平台
如图3所示型号为SB-5500的转子系统动平衡头实物图。图4所示为电主轴转子振动测试实验平台。实验平台由电主轴、动平衡装置控制器、振动传感器、动平衡头等组成。实验平台所采用的电主轴转子系统是自主开发的,型号为HT-170-20000/11,最高转速可达到20 000 r/min。

图3 转子系统的动平衡头实物图 图4 电主轴振动测试实验平台
3.2 高速电主轴转子动平衡实验
采用实验平台进行实验,记录电主轴转子实验平台在添加不同的不平衡量的情况下,电主轴动平衡头自动平衡以及质量补偿优化平衡后的电主轴的振动情况和平衡时间。实验平台通过变频器改变电主轴的转速,实验选择从50 Hz开始,每隔25 Hz记录一次电主轴的振动,直到300 Hz,对应的转速为3000 r/min、4500 r/min、6000 r/min、7500 r/min、9000 r/min、10 500 r/min、12 000 r/min、13 500 r/min、15 000 r/min。实验在电主轴转子平台前端分别添加上10.5 g·mm,21 g·mm和31.5 g·mm三种不平衡量,振动传感器安放在电主轴外壳的前端,实时监测电主轴的振幅。
从图5可以看出电主轴在6000 r/min以及12 000 r/min时的振幅波动较大,这是由于此时电主轴的转子转速分别接近一阶和二阶临界转速。平衡前的最大振幅是出现在转速为15 000 r/min,不平衡量为31.5 g·mm,最大为56.27 μm。最小振幅出现在转速为3000 r/min,不平衡量为10.5 g·mm时,最小为28.77 μm。自动平衡后的最大振幅是出现在转速为15 000 r/min,不平衡量为31.5 g·mm,最大为41.19 μm。最小振幅出现在转速为4500 r/min,不平衡量为10.5 g·mm时,最小为20.39 μm。自动平衡效率最大为44.61%,此时转速为4500 r/min,不平衡量为10 g·mm时,平均平衡率为27.01%。

图5 振幅对比图
经过质量补偿优化平衡后,高速动平衡电主轴转子实验平台振幅相对优化平衡前振幅波动相对平稳,可以将振幅控制在35.00 μm之内。电主轴转子系统的最大振幅是出现在转速为15 000 r/min,不平衡量为31.5 g·mm,最大为32.64 μm。最小振幅出现在转速为3000 r/min,不平衡量为10.5 g·mm时,最小为13.17 μm。动平衡装置的平衡效率最大为54.22%,此时转速为3000 r/min,不平衡量为10.5 g·mm时,平均平衡率为40.90%。优化平衡后电主轴转子系统的振幅相对于自动平衡后的振幅可以平均下降18.62%,最高可以下降41.62%。
图6为优化平衡前后配重块移动步数的比较,平衡装置的配重块移动一步需要5 s。图7为优化平衡时间与优化平衡时间的比较。由于设备的老化和实际工况的原因,不管是未优化平衡还是优化平衡的时间都要远超出平衡的理论时间。未优化时,平衡时间最长在15 000 r/min,需要67 s,移动13.4步,而优化后平衡时间最短在转速3000 r/min时,需要21 s,移动4.2步。其中,在转速为10 500 r/min时,优化后配重块移动步数减小最明显,共减少4.2步。在转速为12 000 r/min时,优化后的平衡时间下降最明显,降低20 s。平衡时间平均下降28.09%,最高可下降38.89%。
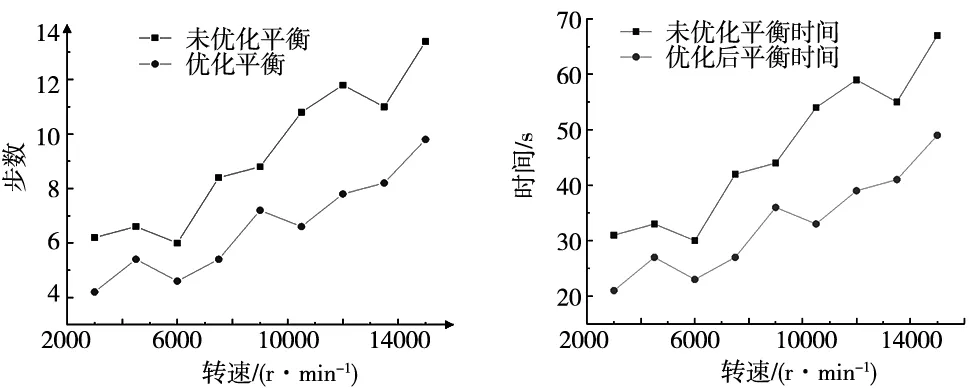
图6 配重块移动步数 图7 平衡时间对比图
4 结论
本文提出一种基于粒子群优化的转子在线动平衡质量补偿优化方法,根据转子在线动平衡机理,建立转子在线动平衡质量补偿优化数学模型,运用粒子群算法实时优化转子在线动平衡最优质量补偿策略,以达到高精度高效率的转子动平衡振动抑制的效果,具体结论如下:
(1)经过转子系统质量补偿优化后的在线动平衡实验表明,优化计算后电主轴转子平衡前后振动幅值最大降低54.22%,平均降低40.90%;
(2)经过质量补偿优化后的转子在线动平衡振动下降量相比未经优化的平衡振动下降量平均提高18.62%;
(3)经过质量补偿优化后动平衡配重块的移动步数及平衡时间相比未经优化的步数和时间最多减少4.2步和降低20 s,平衡时间平均下降28.09%。
