永磁同步电主轴齿槽转矩削弱研究*

于智泽，于慎波，夏鹏澎，翟凤晨，窦汝桐

(沈阳工业大学机械工程学院，沈阳 110870)

0 引言

永磁同步电主轴具有响应速度快、加工精度高、结构紧凑等优点，广泛的应用在高速精密数控机床中[1]，是我国制造业必不可少的核心装备。齿槽转矩产生振动和噪声，进而影响机床加工精度和运行平稳性。齿槽转矩是高精度电主轴最需要考虑的问题之一[2]。

目前，国内外降低齿槽转矩的方法主要从定转子结构、磁极结构和控制方式3个方面进行研究。降低齿槽转矩的方法有：转子分段斜极[3]、定子开辅助槽[4]、定子齿根削角[5]、永磁体分段[6]、永磁体开槽[7]及永磁体削角[8]等。

如今，越来越多学者将电机优化目标与各种群智能优化算法相结合，优化电机最优性能。舒鑫东等[9]利用遗传算法对一台永磁电主轴的永磁体的厚度等参数进行综合优化，结果显著削弱了齿槽转矩。

本文利用等效面电流法对含有定子槽口且永磁体削角的电主轴空载气隙磁场进行建模，利用麻雀搜索法优化出最佳削角宽度和削角弧度。通过与有限元仿真对照分析，验证了含有定子槽口且永磁体削角的电主轴空载气隙磁场有效性，同时也显著降低了永磁同步电主轴的齿槽转矩。

1 齿槽转矩解析分析

根据文献[10]可知，齿槽转矩表达式为：

(1)

式中，W为磁场能量；α为定转子位置角。

磁场能量可近似为气隙和永磁体中的能量，表示为：

(2)

(3)

式中，La为电枢铁心长度；R1为电枢外半径；R2为定子内径。

从式(3)可以看出齿槽转矩与Brn、Gn、电枢槽数等参数有关。可以通过改变磁极结构去改变Brn的幅值，实现减小齿槽转矩，抑制转矩脉动。

2 空载径向气隙磁场建模

2.1 平行充磁削角后永磁体的解析计算

根据文献[11]采用等效面电流法，推导出了永磁体在平行充磁下气隙磁场的解析计算公式，本文在此基础上推导出三种削角后永磁体平行充磁产生的气隙磁场的解析式。

三种削角后永磁体的电主轴结构如图1所示，其中，2η1和2ηk分别为永磁体削角前后的张角；p为永磁体极对数；RS为定子内半径；Rr为转子外半径；hmk为永磁体的厚度；hm1为永磁体削角后厚度。

图1 三种削角后瓦形永磁体一个极的尺寸

当平行充磁时，同圆心不同半径永磁体等效面电流如图2所示，AB和CD上面电流密度J1=Hcbcosη1，BC和AD上面电流密度分别为J2=Hcbsin2η1和J3=-Hcbsin2η1(Hcb为永磁体的矫顽力)。

图2 平行充磁时的等效面电流

平行充磁时，定子内表面由多极永磁体的AB、CD、AD、BC各段所产生的径向气隙磁密为：

(4)

式中，

(5)

式中，L和式(4)中相同。

(6)

式中，L和式(4)中相同。

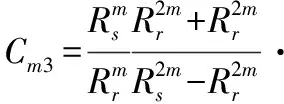
所以定子内表面由多极平行充磁永磁体所产生的径向气隙磁密为：

(7)

为了削角后永磁体平行充磁产生的气隙磁场的解析计算,需要将永磁体两端部分进行模型的等效处理,将永磁体沿着削角方向均匀划分为k段磁极，当k达到一定数值时，认为每段磁极的厚度是均匀的，如图1所示。理论上k的取值越大，计算结果误差越小，但会增加计算量。以下为三种削角后定子内表面由多极平行充磁永磁体所产生径向气隙磁密。

三角形削角后多极永磁体的磁通密度为：

(8)

圆弧削角把原式中hmt换如下公式：

hmt=hmk+r·sinα

(9)

式中，r为削角圆半径；α为极坐标下角度，其中α∈[3π/2,2π]。

圆弧削角后多极永磁体的磁通密度为：

(10)

矩形削角相当于一块永磁体分成三段所产生的气隙磁密叠加。

2.2 定子开槽的气隙磁场计算

当定子开槽后，气隙变为不规则形状，导致气隙磁导率和气隙磁密都会受其影响。相对气隙磁导率是指开槽前后的气隙磁密比值[12]。

把得到开槽后的气隙磁导率通过傅里叶分解得到：

(11)

式中，QS为电主轴槽数；λn为傅里叶系数。

由此得出开槽后气隙径向磁密为：

(12)

2.3 分析与验证

本文研究对象为4极18槽的永磁同步电主轴，利用Maxwell软件绘制永磁电主轴的二维模型并计算出气隙磁密，同时通过等效面电流法得到圆弧削角后的气隙磁密，永磁同步电主轴参数如表1所示。图3为有限元仿真计算结果的二维磁力线分布云图。

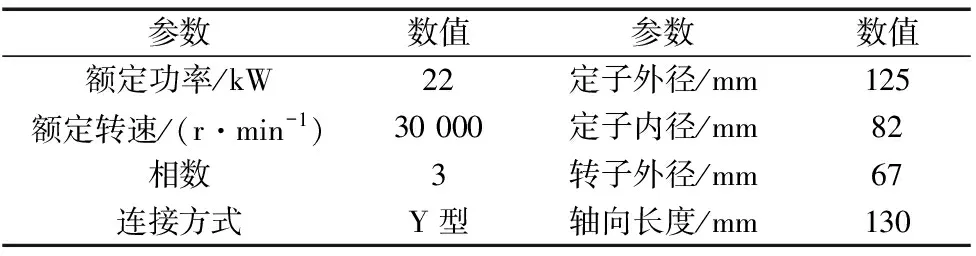
表1 永磁同步电主轴的初始参数

图3 磁力线分布云图

图4为圆弧削角后解析计算的气隙磁密与有限元仿真结果对比，两种波形基本吻合，解析计算气隙磁密有效值为0.717 6 T，有限元仿真的气隙磁密有效值为0.706 7 T，两种计算误差在允许范围内，进一步说明基于等效面电流法削角永磁体气隙解析计算方法的实用性。同理三角削角和矩形削角一样符合。

图4 削角后气隙磁密对比图

3 麻雀搜索算法

麻雀搜索算法(SSA)具有一搜索精度高、收敛速度快且稳定性好，不易陷入局部最优值等优点，此方法均优于现有算法，是一种新型群智能优化算法[13]。

3.1 优化参数设计

利用麻雀搜索法对一台4极18槽三角形削角永磁体的永磁同步主轴进行优化分析。通过抑制气隙磁场谐波畸变率，在合理范围内去搜索永磁体的最佳削角宽度和弧度，达到降低齿槽转矩的目的。削角后宽度hm1和弧度ηk如图1所示。

目标函数和约束条件为：

(13)

通过麻雀搜索算法(SSA)、灰狼优化算法(GWO)和粒子群算法(PSO)分别优化，设置最大迭代次数为100，圆弧削角3种方法的寻优迭代曲线如图5所示。通过比较可知，SSA算法比目前成熟的PSO和GWO算法能快速、准确找到最优的结果。优化出最优参数为hm1为2.25，ηk为36°。同样方法得到圆弧削角最优参数r为2.24，矩形削角最优参数hm1为1.5，ηk为37°。

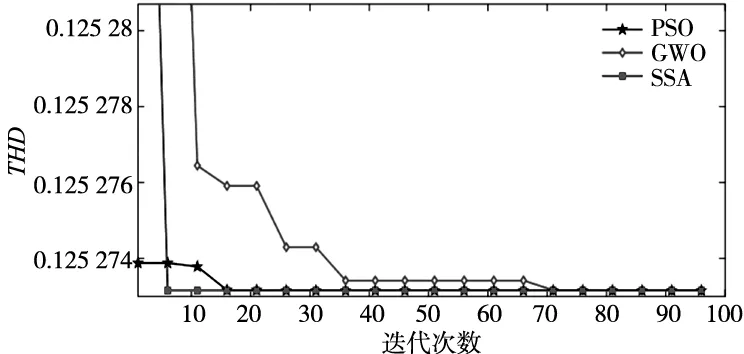
图5 三种寻优曲线对比

3.3 仿真优化结果验证

将永磁体优化前后的永磁同步电主轴用有限元软件Ansoft进行仿真计算，结果如下：

(1)空载齿槽转矩分析。电主轴削角优化前后空载时齿槽转矩的峰值由图6可知，三角削角峰值从156.6 mN·m降低到60.41 mN·m，圆弧削角降到52.11 mN·m，矩形削角降到59.69 mN·m。优化前后谐波对比图如图7所示。三角形和圆弧形基波幅值变化不大，谐波幅值明显降低，尤其5次谐波几乎消掉。矩形削角虽然谐波幅值明显下降，但是基波幅值下降也多。说明削角永磁体可以有效地降低齿槽转矩。

图6 优化前后空载齿槽转矩对比

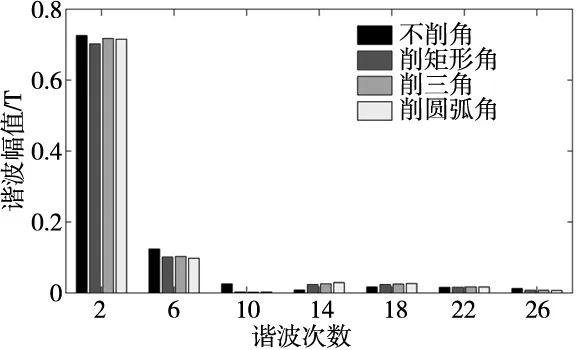
图7 优化前后气隙磁密谐波分析

(2)负载转矩脉动分析。电主轴在负载情况下的转矩脉动，可以通过改变永磁体削角参数进一步减小。转矩脉动计算公式如下：

(14)

永磁同步电主轴优化前后转矩脉动对比如表2所示，在平均转矩变化很小的条件下，三角削角的转矩脉动降低了46%，圆弧削角的转矩脉动降低44%。矩形削角的转矩脉动虽然降了48%，但是平均转矩下降的多。

表2 永磁同步电主轴转矩脉动

综合上述分析，三种削角都是最优结果情况下，圆弧削角效果最好。削角优化后可以更有效地降低转矩脉动。

4 结论

本文对削角的永磁同步电主轴空载气隙磁场建模，利用麻雀搜索算法来优化永磁同步电主轴。研究结果表明：

(1)通过基于等效面电流法对三种永磁体削角的永磁同步电主轴空载气隙磁场计算分析。验证了该方法的实用性。利用麻雀优化算法对气隙磁场的谐波畸变率进行了优化，确定了齿槽转矩最低的永磁体结构参数。

(2)永磁同步电主轴三种永磁体结构优化后，综合考虑，圆弧削角结果最优。圆弧削角永磁体在平均转矩基本未变情况下，其齿槽转矩的峰值从156.6 mN·m降低到52.11 mN·m，转矩脉动降低了44%。有效地抑制齿槽转矩和转矩脉动，对提高机床的寿命和加工精度有重要意义。