基于改进蝗虫优化算法的车身焊接机器人路径规划*

李国奎，刘永明

(1.四川建筑职业技术学院机电与信息工程系，德阳 618000；2.河南科技大学材料科学与工程学院，洛阳 471000)

0 引言

汽车车身焊接生产线上目前已大量使用机器人进行焊接工作[1-2]，但是，依靠人工经验来进行机器人焊接路径的规划是目前众多企业采用的方式，这就导致路径规划耗时长、可靠性低，从而影响加工效率。因此，研究焊接机器人路径自动规划算法，是汽车智能制造技术重点研究方法[3-4]。

随着智能算法的不断发展，不少学者将机器人焊接路径规划问题进行转化，从而提出了基于智能算法的机器人焊接路径规划新方法。吕文壮等[5]为提高车身焊接机器人路径规划的效率，使用改进蚁群算法进行路径规划，显著缩短了路径规划的时间，提高了效率；田天鹏[6]提出了改进粒子群算法进行车身门板焊机器人路径规划，获得了比普通粒子群算法更好的效果；裴跃翔等[7]以车身前机匣总成的机器人焊接路径规划为例，对嵌入筛选操作的遗传算法的有效性进行了验证；程小洪[8]提出改进果蝇优化算法进行汽车饰件多焊接机器人协同焊接的路径规划，实现了任务均衡分配和耗时缩短。

上述研究表明，基于智能算法的焊接机器人路径规划已成为一种有效的焊机机器人路径规划方法。通过模拟蝗虫的觅食行为，蝗虫优化算法[9](grasshopper optimization algorithm,GOA)，因可操作性强、调控参数少、收敛速度快等优点，目前已在众多的优化问题求解中得到了应用[10-13]，实现了各优化问题的有效求解。因此，这也为焊接机器人路径规划提供了一种新的方法选择。但是，一方面，基本GOA算法中种群的初始化是通过随机方式确定的，这就有可能导致初始的种群分布并不均匀，从而影响下一步的收敛；另一方面，基于GOA算法中是通过一个线性递减的参数来调控算法前后期搜索能力的，而实际上线性递减的参数并不能很好的起到平衡作用。因此，有必要针对上述问题对其进行改进，从而提升其在焊接机器人路径规划中的效果。

本文为提高焊接机器人路径规划的效率，针对GOA存在的不足，通过引入贝塔函数实现种群的初始化更为均匀，通过引入非线性惯性权重实现前后期搜索能力的平衡，由此提出改进蝗虫优化算法(improved grasshopper optimization algorithm,IGOA)并进行焊接机器人路径规划。车身前后门焊接路径规划实例表明，相比于其它一些方法，IGOA缩短的焊接路径、减少了耗时、提升了效率，且稳定性更好。

1 焊接机器人路径规划建模

进行焊接机器人的焊接路径规划，其目的是通过高效、快速的方法为焊接机器人找到一条尽可能短的焊接路径，保证焊接机器人在完成规定任务的同时，提高工作效率。焊接路径规划可简单描述为：从起始焊点开始，焊接机器人将N个焊点都焊接完成后，再回到起始焊点，并且保证每个焊点只经过1次。这一问题实际上和旅行商问题(travelling salesman problem,TSP)十分相似。

假设N个焊点的集合为W={w1,w2,…,wN}，则其中某一条焊接序列为wφ=(wφ(1),wφ(2),…,wφ(N))，其中wφ(1)∈W(1≤i,j≤N)。两个焊点之间的距离表示为d(wφ(i),wφ(j))且大于等于0，其中(wφ(i),wφ(j))∈W(1≤i,j≤N)。焊接序列总长度则可表示为：

(1)

在焊接机器人的路径规划中，核心问题就是要保证Sφ尽可能地短，以便减少焊接耗时，提高工作效率。

2 蝗虫优化算法

GOA算法中的蝗虫个体i所在位置Xi表示待求优化问题的一个候选解，其主要由个体间作用力、风力、重力等3种因素决定，数学模型可表示为：

Xi=Si+Gi+Ai

(2)

式中，Si为个体间相互作用力，其计算公式为：

(3)

式中，dij为蝗虫i与蝗虫j之间的距离；dij为蝗虫i所在位置到蝗虫j所在位置的单位向量。

(4)

式(3)中的s函数为计算蝗虫种群间相互作用力的函数，其表达式为：

(5)

式中，f为吸引强度参数；l为吸引尺度参数。

式(2)中的Gi为外界风力的影响，其计算方式为：

Gi=-geg

(6)

式中，g为重力常数；eg为单位向量并指向重心。

式(2)中的Ai为外界重力的影响，其计算方式为：

Ai=μew

(7)

式中，μ为漂移常数；ew为单位向量且与风同向。

将式(3)、式(6)和式(7)代入式(2)中，可得：

(8)

由于式(8)在优化问题中并不适用，因此，GOA算法的提出者在不考虑重力的影响下，且假设风总是朝向目标，将式(8)修正为：

(9)

式中，bmax为搜索空间上界；bmin为维搜索空间下界；Td为蝗虫种群中的目前最优个体所在的位置；c主要用来调控算法的全局和局部搜索能力，它会随着迭代次数的增加而自适应的变化：

(10)

式中，cmax和cmin分别为系数c的最大和最小值；t和T分别为当前迭代次数和最大迭代次数。

3 改进的蝗虫优化算法

对于智能算法而言，一般都需要对种群进行初始化且初始化方式对后续收敛具有一定的影响，GOA算法也不例外。在GOA算法中，种群的初始化是通过随机的方式确定的，这种方式容易出现种群在解空间范围内初始化不均匀的情况，进而对下一步的收敛产生影响。同时，GOA算法中使用到的调控参数c的作用是调控算法的全局和局部搜索能力，它是随迭代次数的增加而线性递减的，这种线性递减的方式实际上并不能实现搜索能力的平衡。因此，本文为克服上述不足，对GOA算法进行改进设计，提出IGOA算法。

3.1 贝塔函数初始化

贝塔分布[14]需要调控的参数简单，可以在给定的空间范围内产生均匀的分布，因此，将其用于在解空间范围内生成蝗虫种群的初始化位置。贝塔分布用到的是贝塔函数，又可成为B函数或者第一欧拉积分，它满足连续性和对称性要求，它的表达式为：

(11)

式中，P和Q均大于0。

利用贝塔函数进行种群初始化的策略为：

首先，通过贝塔函数在解空间范围内生成一个可行解，表示为：

X=[x1,x2,…,xd]

(12)

式中，d为搜索空间的维度；xi∈[ai,bi]。

而后，进行反向解的求取，即求得：

(13)

3.2 非线性惯性权重

对于式(9)而言，外部和内部的调控参数c均是通过式(10)计算得到。而事实上，在前期搜索中，c值需要为较大值且变化速率应较小，这样才能保证能有较长的时间在广阔的范围进行全局搜索；在后期搜索中，c值需要为较小值且变化速率应较大，这样才能保证在小范围内进行精细快速的搜索。因此，将式(10)中的调控系数c的计算公式调整为：

(14)

式中，ω为一个非线性惯性权重系数，它的计算公式为：

(15)

改进后的式(14)，使得在迭代前期，c的值较大且下降速率较慢，一定程度上可以增强种群在前期的全局搜索能力；在迭代后期，c的值较小且下降速率较快，一定程度上可以增强种群在后期的局部搜索能力，这样就实现了算法前后期搜索能力的平衡。

3.3 IGOA算法流程

在GOA算法的基础上，通过贝塔函数进行种群的初始化，通过非线性惯性权重实现调控参数c计算方式的改变，即可得IGOA算法，其算法流程如图1所示。

图1 IGOA算法流程图

4 算法应用实例

4.1 焊接对象

本文以某型汽车车门总成为研究对象，进行焊接路径的规划，车门总成包括前门和后门两部分，其中，前门一共有51个焊点，后门一共有62个焊点。由于车门的结构较为扁平，各焊点之间纵向上的距离差距很小，所有焊点几乎是分布在同一的平面上，因此，为将问题简化，不考虑焊点之间的纵向距离，将所有焊点处理到二维平面上，得到如图2所示的焊点二维平面分布图。

(a) 前门 (b) 后门

4.2 结果分析

利用本文所提IGOA算法对焊接机器人的路径进行规划，并完成图3所示前、后车门的焊接。为了对比分析不同方法的优劣，本文还利用基本GOA方法、文献[5]中的改进蚁群算法(IACO)、文献[6]中的改进粒子群算法(IPSO)、文献[8]中的改进果蝇优化算法(IFOA)等方法对焊接机器人的路径进行规划，并完成图2所示前、后车门的焊接。需要说明的是，IACO、IPSO和IFOA等3种方法在原文献中均已用于焊接机器人路径规划并完成车身的焊接工作，具有不错的效果。在利用各方法进行路径规划时，几种算法的种群规模均设置为30、最大迭代次数均设置为100；IACO、IPSO和IFOA等方法需要的其余参数均参照原文献进行设置。

利用上述提到的IGOA、GOA、IACO、IPSO和IFOA这5种方法依次对前、后车门焊接路径进行规划，每种方法对前、后车门进行焊接路径规划时，为减小偶然因素，均独立进行20次计算，而后进行20次计算结果的统计分析。5种方法计算得到总焊接路径长度可视化结果如图3所示，几种评价指标的统计结果如表1所示，最短焊接路径焊接示意图如图4所示。

从图3中可知，无论是对于前门的焊接还是后门的焊接，在20次独立计算中，各方法在每次计算时，规划得到的总焊接路径长度是不同的，但从总的曲线分布趋势上看，IGOA在20次计算中得到的结果基本上都是处于最下方的位置，即得到的总焊接路径最短，特别是相较于IPSO，曲线下降的幅度很大。并且，从结算结果的波动程度上来看，IGOA曲线的波动程度也较小，即计算的稳定性更强。

(a) 前门 (b) 后门

从表1中可知，无论是对于前门的焊接还是后门的焊接，在5种评价指标中，除在“最短路径耗时”这一评价指标上，IGOA的耗时较GOA有所增加外，其余评价指标均是要优于其余4种方法的。如在最短、最长路径这两个评价指标上，IGOA得到的最长路径比IACO、GOA和IPSO获得的最短路径还要短，且仅比IFOA获得的最短路径长了约2 mm，可见IGOA规划的焊接路径明显比其余4种方法短；又如标准差评价指标，IGOA的20次结算结果标准差远小于其余4种方法，可见其计算稳定性更强，这一结果和图4种IGOA的曲线波动程度更小相对应；再如最短路径耗时指标，IGOA由于增加了贝塔函数初始化和非线性惯性权重策略，在耗时上较GOA略有增加，但增加幅度仅在1 s上下，而相比于其余3种方法，特别是IABC和IPSO方法，耗时则是缩短了约2～3倍。

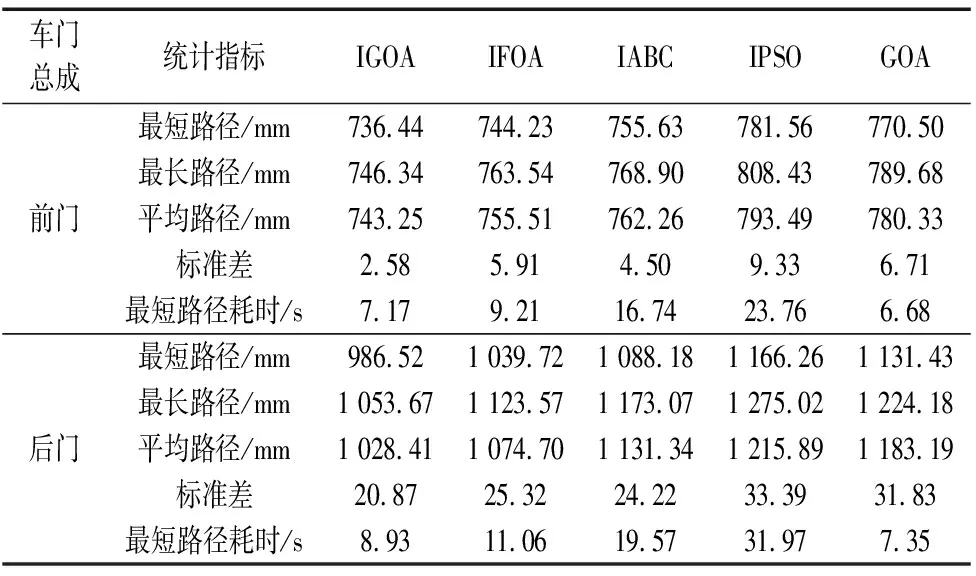
表1 计算结果统计

由图4可知，无论是对于前门的焊接路径，还是后门的焊接路径，5种方法规划得到的焊接路径即有相似的地方，也有明显不同的地方。如图4a中，IGOA、IFOA和IACO规划得到的焊接路径不存在路径交叉的情况，但在细节上可以看出焊接轨迹还是存在差别；图4b中，虽然5种方法得到的焊接轨迹均没有路径交叉的情况出现，但是仔细对比，各方法得到的焊接轨迹的差别还是比较明显的。

(a) 前门

(b) 后门

图3、表1和图4的结果表明，本文IGOA在焊接机器人焊接路径规划中，相比于其余4种方法，可以得到更短的焊接路径，路径规划所需要的时间更短，且具有更强的计算稳定性。

5 结论

针对焊接机器人焊接路径规划问题，提出了用于车身焊接机器人路径规划的改进蝗虫优化算法，并进行了实例应用，得到如下结论：

(1)引入贝塔函数进行种群初始化，引入非线性惯性权重平衡算法前后期搜索能力，二者的结合改善了GOA算法的性能；

(2)从焊接路径长度、时间消耗、计算稳定性等方面综合对比了IGOA与GOA以及其余3种方法的性能，验证了IGOA在性能上更具优势；

(3)通过对IGOA算法的研究，为提高焊接机器人路径规划效率、缩短路径长度等方面提供了一种新的有效方法。