含砂原油对方形补偿器的冲蚀模拟

陈一鸣，陈 微，刘宏达，何金宝

（1.辽宁石油化工大学 石油天然气工程学院，辽宁抚顺 113001；2.辽宁石油化工大学 石油化工学院，辽宁抚顺 113001；3.辽河油田钻采工艺研究院，辽宁盘锦 124010）

0 引言

为了研究固体颗粒对相关管道和设备内壁面的影响机理及规律［1］，国内外相关学者对管道常用管件处的冲蚀现象进行了广泛的研究［2-3］，其中，梁光川等［4］通过对弯管内压力分布、进口流速进行分析，得到了局部流场变化对管内壁冲蚀作用的影响，验证了易腐蚀部位；彭文山等［5］通过改变固体颗粒粒径，得到了直径相对较小的固体颗粒对弯管的冲蚀速率高于大直径颗粒；偶国富等［6］通过建立弯管处随腐蚀产物保护膜形状变化而改变的流固界面模型，计算了壁面切应力及弹性应变量，从而得到冲蚀严重区域，进而验证了该模型的可行性；张孟昀等［7］通过分析弯管与盲通管内颗粒的运动轨迹，验证了流体涡旋现象及颗粒的局部积存能够缓解固体颗粒对管道的冲蚀作用；陈宇等［8］通过改变三通管连接结构尺寸，证明了2种结构三通管的内壁面冲蚀速率随进口流速及颗粒质量流率增加而增大，有球体弯头的三通管的冲蚀磨损程度相对较小；冯留海等［9］利用修正后的冲蚀模型，计算得到了突扩及突缩管内颗粒对管壁冲蚀的相关数据，其与实验结果吻合度较高；王博等［10］对某输油管线中13处局部管件的冲蚀速率进行计算，得到了较为准确的实际设计管线中的冲蚀情况，为管道建设过程中的局部减蚀提供了数据支撑。

综合国内外冲蚀研究进展，相关实验及模拟主要以某特定物理模型为对象，在此基础上分析该模型内流体速度场、压力场及固体颗粒轨迹等对冲蚀机理的影响［11］，涉及相关影响因素丰富、针对性强，并提出了各种常用管件内冲蚀速率及冲蚀区域的分布规律，从实际出发，先前的研究模型大多较为简单且缺少降低冲蚀作用的具体措施，相关成果与实际结合过程较为复杂，缺乏对比性与应用性。

通过总结管道常见失效管件的研究成果发现，弯管是受冲刷腐蚀最严重的管件之一，单一弯管内部冲蚀机理研究日趋成熟［12］，而被广泛应用、具有局部四弯头结构且流动变化更为复杂的方形补偿器内部的冲蚀作用却鲜有研究，因此，在弯管冲蚀研究基础上，以用于管道热应力补偿的标准方形补偿器为研究对象，对比分析不同弯径比条件下、热补偿能力相同的4种型号补偿器内的冲蚀现象，选择相同的热补偿能力可以保证4种补偿器相互间的可替代性，不同的弯径比可以为补偿器提供更灵活的设计空间，从而更好的适应工程实际，实现补偿器的减蚀设计与最优选型。

1 数学模型

1.1 湍流模型

根据管内流体实际流动情况，流体处于全面发展的完全湍流状态，分子间黏性可忽略，因此选用广泛应用的标准k-ε两方程模型。

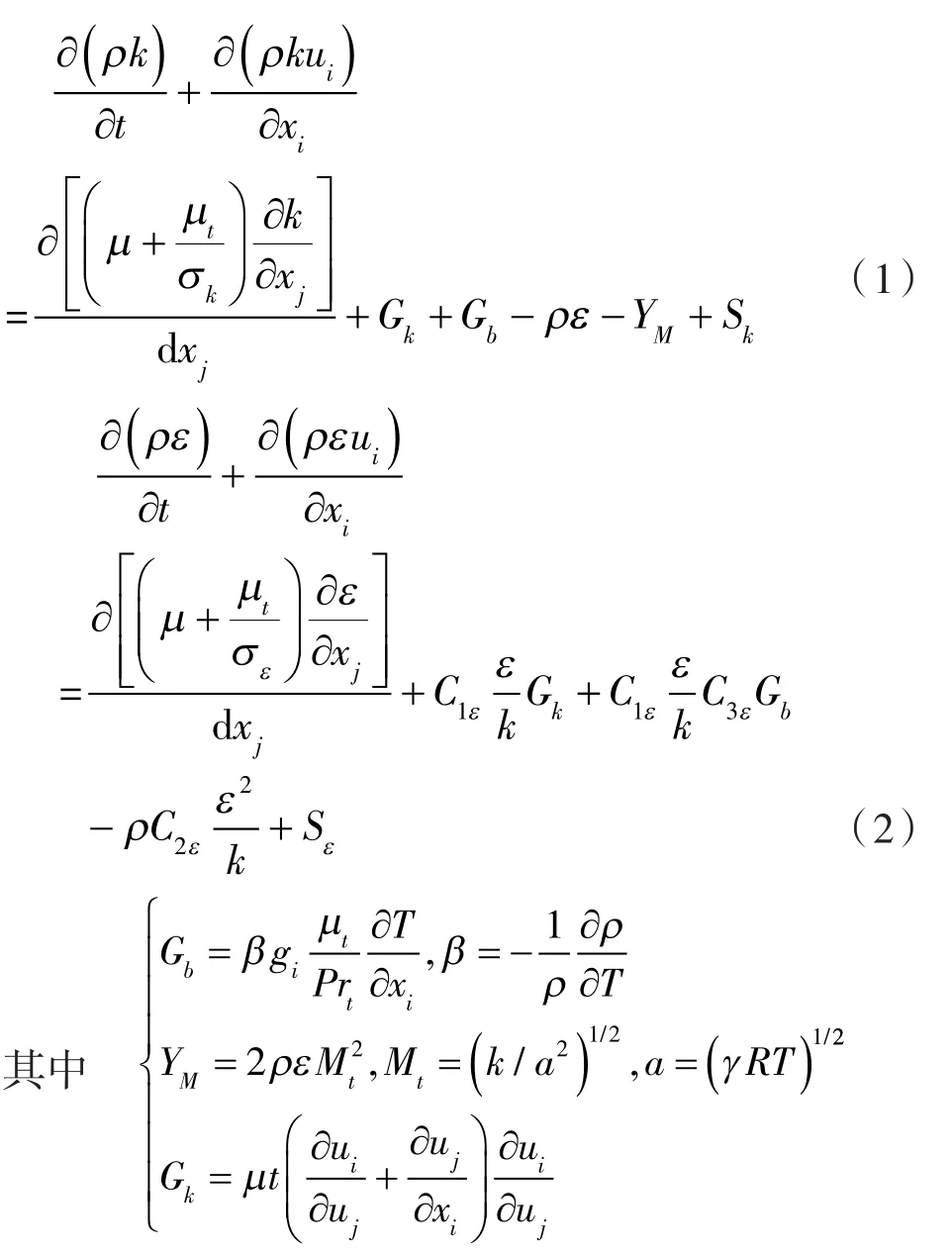
式中 Gk——由速度梯度产生的湍动能附加项；

Gb——由浮力引起的湍动能产生项；

Prt——湍动普朗特数，Prt=0.85；

YM——可压湍流脉冲的扩张项；

gi—— 当地重力加速度在i方向上的分量，m/s；

β ——热膨胀系数，K；

σε，σk—— 湍动能及湍动耗散率［13］，σε=1.3，σk=1.0；

Sk，Sε——源相，Sk=0，Sε=0；

k ——湍动能，J；

ε ——耗散率，%；

T ——温度，K；

Mt——湍动Mach数；

α ——声速，m/s；

C1ε，C2ε，C3ε—— 经验常数，C1ε=1.44，C2ε=1.92，C3ε=0.09。

由于连续相可近似为不可压缩流体，因此，Gb=0，YM=0。

1.2 固体颗粒运动方程

由于模拟过程中固体颗粒体积分数低于10%，可按离散相处理，固体颗粒对连续相的影响可忽略，通过对固体颗粒作用力微分方程积分求解得到离散相轨迹方程。

式中 up——固体颗粒速度，m/s；

FD（u-up）—— 固体颗粒的单位质量曳力，N；

u ——连续相速度，m/s；

ρp——固体颗粒密度，kg/m3；

ρ ——连续相密度，kg/m3；

μ ——流体动力黏度，Pa·s；

dp——固体颗粒直径，m；

CD——曳力系数；

Re ——相对雷诺数。

由于固体颗粒粒径介于亚观尺度与亚毫米尺度之间［14］，Fi只作为附加质量力进行计算。

1.3 冲蚀与沉积模型

固体颗粒与管内壁的相互作用与材料局部沉积现象可通过冲蚀速率及沉积速率进行量化，数学计算模型如下［15-17］：

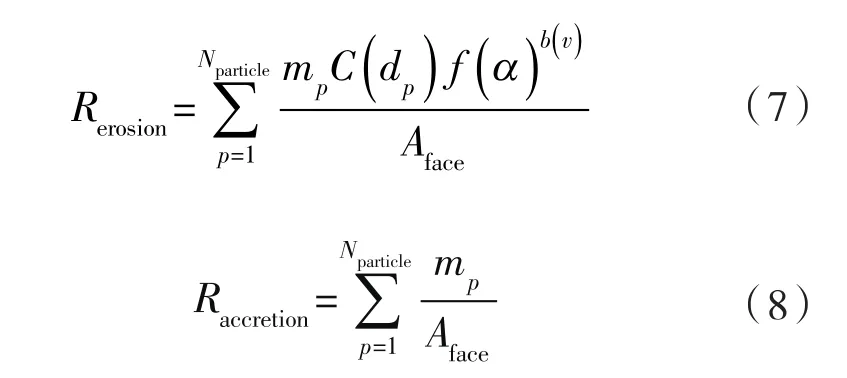
式中 Rerosion——冲蚀速率，kg/（m2·s）；

mp——固体颗粒质量，kg；

C（dp）——固体颗粒粒径的函数［18］；

α ——固体颗粒与壁面间的冲击角度，rad；

f（α）——冲击角函数；

v ——固体颗粒相对于壁面速度，m/s；

b（v）——相对速度函数；

Raccretion——沉积速率，kg/m2。

2 几何模型及网格划分

2.1 方形补偿器尺寸及结构

管线公称直径DN200，内径207 mm，壁厚6 mm，直管段长度H=200 m，管线钢线膨胀系数0.012 mm/（m·℃），安装温度与环境温度温差为40 ℃。为保证4种补偿器热补偿量相同，根据计算得到的管段热伸长量96 mm，确定热补偿量为100 mm，计算4种方形补偿器所需要的几何尺寸见表1，补偿器各弯径比为1.5，4种标准补偿器各弯管处按流体流经顺序依次定义为A，B，C及D弯管，几何模型如图1所示。

表1 4种方形补偿器尺寸Tab.1 Sizes of four square compensators

图1 补偿器结构尺寸Fig.1 Compensator structure size

2.2 网格及无关性检验

为保证计算精度，4种标准方形补偿器均采用结构化网格进行划分［19］，近壁面区域设置4层边界层，弯管处根据冲蚀预计算进行独立加密处理，提高冲蚀集中区计算精度，降低整体计算成本，模拟中所用网格模型无关性检验满足计算要求［20］，精度波动数量级均小于 1×10-3，网格模型如图2所示。

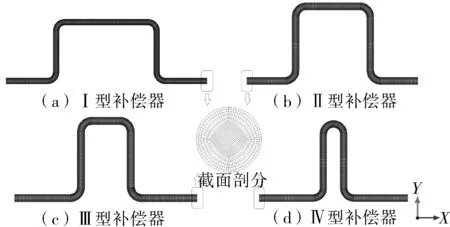
图2 补偿器网格划分Fig.2 Compensator grid division

2.3 相关物性及参数设定

管道内流动介质为含砂原油，原油密度为960 kg/m3，动力黏度 0.048 Pa·s，固体颗粒为惰性球形沙粒，密度1 500 kg/m3。管道进口流速与所携带固体颗粒速度均为2.5 m/s，运行压力3.0 MPa，雷诺数 Re=1.035×10-4，重力 g=9.81 m/s2，方向与补偿器外伸方向保持垂直，由于固体颗粒粒径大于10 μm且不存在温度梯度，可忽略Saffman升力［21］、布朗力及热泳力［22-23］。

表2 边界条件Tab.2 Boundary conditions

3 计算结果分析

3.1 颗粒质量流率对冲蚀速率影响

管道内原油所携带固体颗粒的质量流率直接影响固体颗粒的分布密度，进而影响冲蚀速率，在固体颗粒粒径0.5 mm、进口流速2.5 m/s与热补偿能力100 mm不变的条件下，对质量流率在0.01～0.10 kg/s范围内4种标准1.5D方形补偿器内的冲蚀速率进行计算，计算结果如图3所示，4种补偿器内壁面的冲蚀速率均随质量流率的增加而增大，二者均近似为线性正相关，其中，Ⅰ型补偿器的冲蚀速率与质量流率的线性拟合优度好于其它3种补偿器，具有更明显的线性特征，拟合曲线 y=179.5x＋ 0.3，R2=0.997。

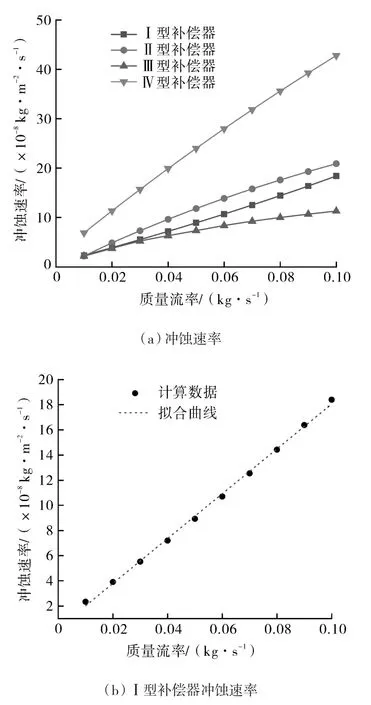
图3 冲蚀速率与质量流率关系曲线Fig.3 The relationship between erosion rate and mass flow rate

4种补偿器内的冲蚀集中区域具有相似的分布规律，各型号补偿器内的最大冲蚀速率均集中于B弯管与C弯管区域，随着颗粒质量流率的增加，B弯管与C弯管处的冲蚀速率不断上升，冲蚀区域不断扩大。在4种补偿器中，A弯管处均未发生明显的冲蚀现象。对于发生在各型号补偿器D弯管处的冲蚀现象，由于Ⅰ，Ⅱ，Ⅳ型补偿器内的冲蚀速率高于Ⅲ型补偿器，这3种补偿器D弯管处的冲蚀速率相对于其它弯管处的冲蚀速率可忽略不计，而Ⅲ型补偿器内的冲蚀速率较低，其在D弯管处的冲蚀速率相对于其它弯管处的冲蚀速率不可忽略，其冲蚀云图如图4所示。

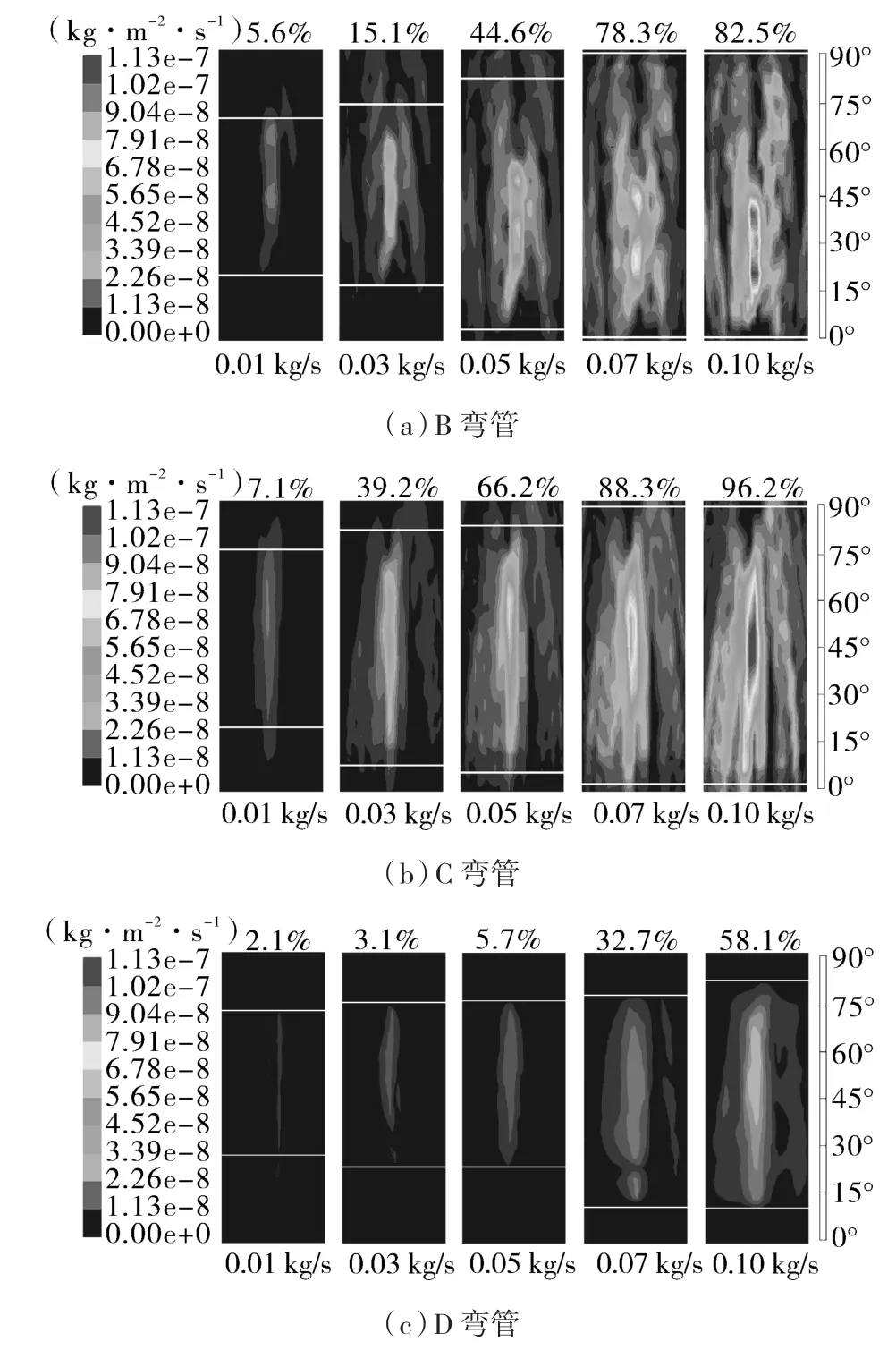
图4 Ⅲ型补偿器B，C，D弯管外弧面区冲蚀速率及区域占比Fig.4 Erosion rate and area proportion of the outer arc surface area of B，C，D-bend of type Ⅲ compensator

3.2 颗粒粒径对冲蚀速率影响

在保证进口流速2.5 m/s、质量流率0.01 kg/s与热补偿能力100 mm不变的情况下，通过改变固体颗粒粒径，计算不同粒径下固体颗粒对4种标准方形补偿器的冲蚀速率，粒径范围选取0.1～1 mm，计算结果如图5所示。结果显示，在固体颗粒粒径小于0.4 mm情况下，Ⅰ、Ⅱ、Ⅳ型补偿器内冲蚀速率随粒径增加而减小，Ⅲ型补偿器则呈上升趋势，这主要是由于随着固体颗粒粒径的增加，固体颗粒自身动能增加，受原油粘滞力束缚减弱［24］，Ⅲ型补偿器内固体颗粒对壁面冲蚀集中区域由C弯管处提前至B弯管处，减少了固体颗粒与外伸水平管段间的碰撞损失，使B弯管处局部冲蚀速率加剧，而Ⅰ、Ⅱ、Ⅳ型补偿器内冲蚀区域位置受粒径变化影响较小，固体颗粒在局部的集聚缓解了后续固体颗粒对管内壁的冲蚀作用；在0.4～0.6 mm区间内，Ⅱ与Ⅳ型补偿器内冲蚀速率先减小后增加，Ⅰ与Ⅲ型补偿器保持递减趋势，此时Ⅰ型补偿器内固体颗粒对管壁的冲蚀仍未受到粒径继续增加所带来的影响，Ⅲ型补偿器则开始进入由于冲蚀集中区提前至B弯管处所带来的固体颗粒集聚所导致的冲蚀速率下降区间，而Ⅱ与Ⅳ型补偿器内冲蚀速率由于粒径的增加，原有的动态平衡机制被固体颗粒自身惯性力的增加所破坏［25］，冲蚀集中区的冲蚀速率开始上升；当固体颗粒粒径大于0.6 mm，Ⅰ与Ⅲ型补偿器内冲蚀速率先减小后增加，而Ⅱ与Ⅳ型补偿器内冲蚀速率保持递减，此时，Ⅰ型补偿器与Ⅲ型补偿器内固体颗粒动态聚集的平衡刚刚被持续增加的大粒径固体颗粒打破，Ⅱ与Ⅳ型补偿器则开始进入由更大粒径固体颗粒集聚所主导的局部减蚀的新周期，4种补偿器内冲蚀速率随固体颗粒粒径变化均出现一次明显的波动过程，Ⅱ补偿器与Ⅳ型补偿器相较于Ⅰ补偿器与Ⅲ型补偿器较为提前，这主要是由于之前Ⅲ型补偿器冲蚀集中区随固体颗粒粒径增加由C弯管处转至B弯管处，而Ⅰ型补偿器较长的水平外伸长度使流体在B，C两处弯管间湍动效应减弱，固体颗粒破坏平衡需要更高的动能，从而延长了Ⅰ型补偿器的冲蚀周期。与变质量流率情况类似，4种补偿器中Ⅳ型补偿器的冲蚀速率明显高于其它3种补偿器。

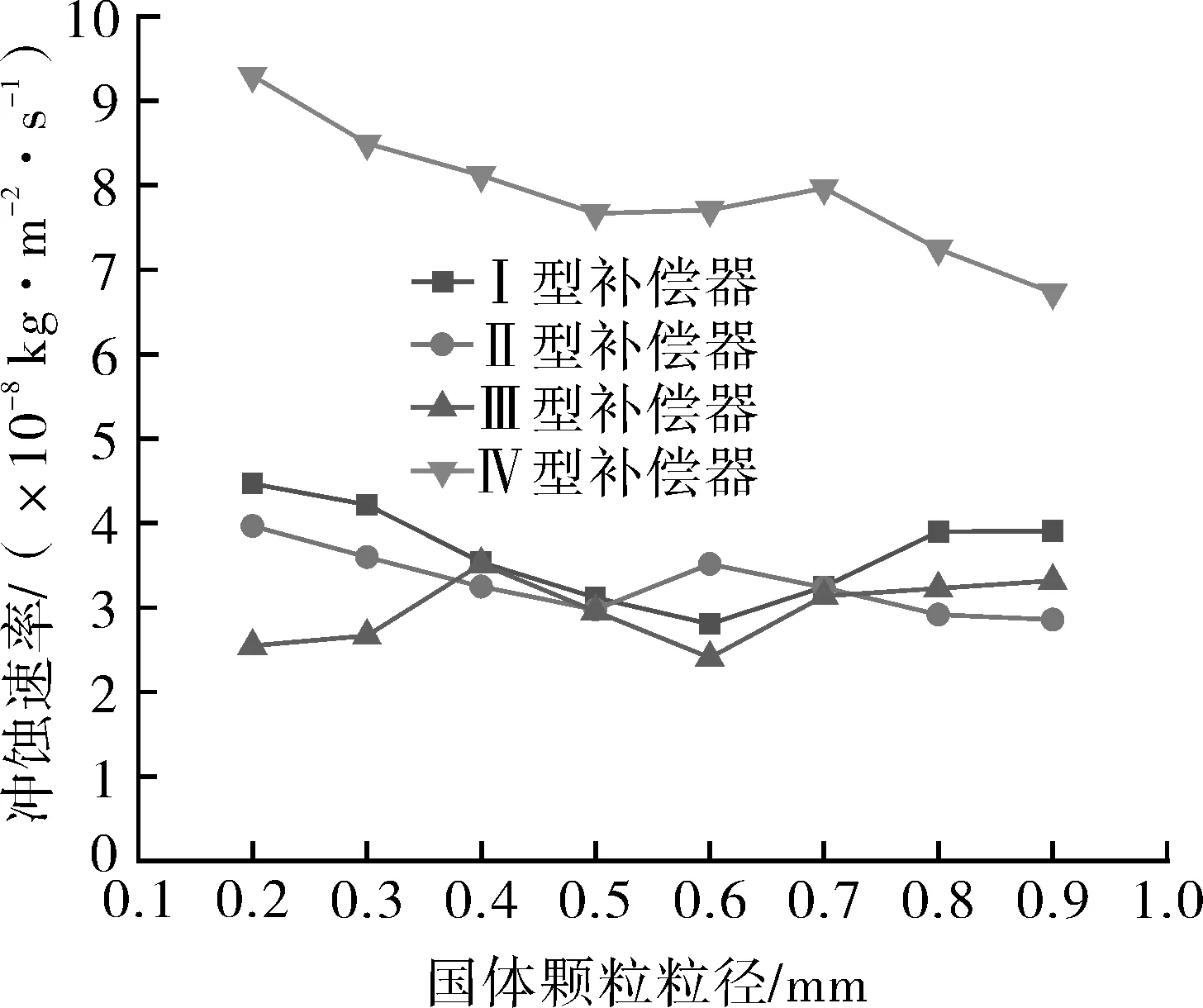
图5 冲蚀速率与固体颗粒粒径关系曲线Fig.5 The relationship between erosion rate and solid particle sizes

3.3 弯径比对冲蚀速率影响

根据方形补偿器的类型，对1.5D～4.0D弯径比条件下的4种热补偿能力相同的标准方形补偿器内的冲蚀速率分别进行计算，固体颗粒粒径为0.5 mm，固体颗粒质量流率0.01 kg/s，进口流速2.5 m/s，计算结果如图6所示。

图6 冲蚀速率与弯径比关系曲线Fig.6 The relationship between erosion rate and bending diameter ratio

根据计算结果，Ⅰ型补偿器内固体颗粒随连续相运动轨迹可分为4个阶段，在第一阶段（1.5D～2.75D），固体颗粒对补偿器的冲蚀作用以点蚀为主，随弯径比的增加，冲击角度减小［29-31］，冲击角对管内壁影响如图7所示，固体颗粒对壁面的切削作用转变为范围更大的磨蚀［27］，能量释放周期相对延长，冲蚀速率降低，冲蚀范围扩大，随着弯径比继续增加，固体颗粒的运动进入第二阶段（2.75D～3.25D），补偿器最大冲蚀区域后移至D弯管处，固体颗粒与前3处弯管只发生轻微摩擦，保留了自身大部分动能，冲蚀速率逐渐增大，与第二阶段相比，固体颗粒在第三阶段（3.25D～3.75D）对A，B，C等3处弯管的磨蚀加剧，缓解了第二阶段固体颗粒对D处的冲蚀作用，最大冲蚀速率开始下降，进入最后阶段时（4.0D），较大的弯径使固体颗粒与壁面的碰撞次数减少，固体颗粒在内壁面停留时间延长，最大冲蚀速率出现在B弯管外弧面区，且对此处造成冲蚀的固体颗粒在此之前并未与壁面反生碰撞，冲蚀速率上升明显。

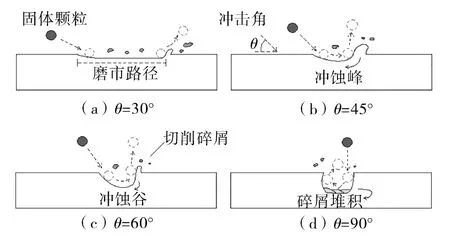
图7 固体颗粒冲击角对管壁冲蚀与磨蚀作用机理Fig.7 The mechanism of the impact angle of solid particles on tube wall erosion and abrasion

Ⅱ型补偿器内冲蚀区域位置随弯径比变化明显，在1.5D条件下，冲蚀区域集中在B，C 2处弯管外弧面区，随弯径比增加，D弯管外弧面区冲蚀现象增强，C弯管外弧面区冲蚀现象减弱，B弯管处始终是冲蚀最严重区域，最大冲蚀速率达到3.03×10-8kg/（m2·s）；当弯径比增加到 2.75D 时，C弯管处不再发生冲蚀现象，冲蚀最严重的区域由B弯管处移至D弯管处，B弯管处冲蚀速率下降；随弯径比继续增加，C弯管处冲蚀加剧，B，D两处弯管冲蚀减弱，当弯径比在3.5D～4.0D范围内变化时，各处冲蚀范围开始扩大，A弯管内弧面区与B弯管外弧面区及C弯管外弧面区与D弯管外弧面区之间先后出现连续磨蚀区域。

在弯径比为1.5D时，Ⅲ型补偿器A，D两处弯管均未发生无明显冲蚀，随弯径比的增加，最大冲蚀区域始终出现在B弯管外弧面区，D弯管处冲蚀速率逐渐上升，C弯管处冲蚀速率下降，当弯径比达到2.5D时，发生最大冲蚀速率区域开始由B弯管处向C弯管处过渡，C弯管处冲蚀速率开始上升，B，D两处弯管冲蚀速率开始减弱，并随着弯径比增加继续向D弯管处过渡，当弯径比达到3.0时，最大冲蚀速率出现在D弯管处，弯径比继续增加，最大冲蚀速率区域再次过渡回C弯管处，并持续增加，B，D两处弯管冲蚀速率及冲蚀面积逐渐减小。

与其它3种补偿器相比，Ⅳ型补偿器的冲蚀速率随弯径比增大有更为明显下降趋势，其最大冲蚀速率由 1.5D 时的 6.89×10-8kg/（m2·s）降至4.0D 时的 1.62×10-8kg/（m2·s），当弯径比增加到1.75时，在C弯管外弧面区开始形成连续的磨蚀区域，B弯管处仍以点蚀为主，随着弯径比继续增加，固体颗粒与内壁面的冲击角度不断减小，磨蚀范围不断扩大，当弯径比增加到2.25，固体颗粒与B弯管外弧面间的冲击角下降到30°以下［28］，B，C两处弯管的磨蚀区域呈带状分布在补偿器外伸段0°～160°外弧面区范围内，计算结果如图8所示，并随弯径比增加继续延伸，磨蚀范围从弯径比为1.75的Ⅳ型补偿器B弯管0°撞击点一直延续至弯径比4.0的Ⅳ型补偿器C弯管与D弯管间的240°管段。

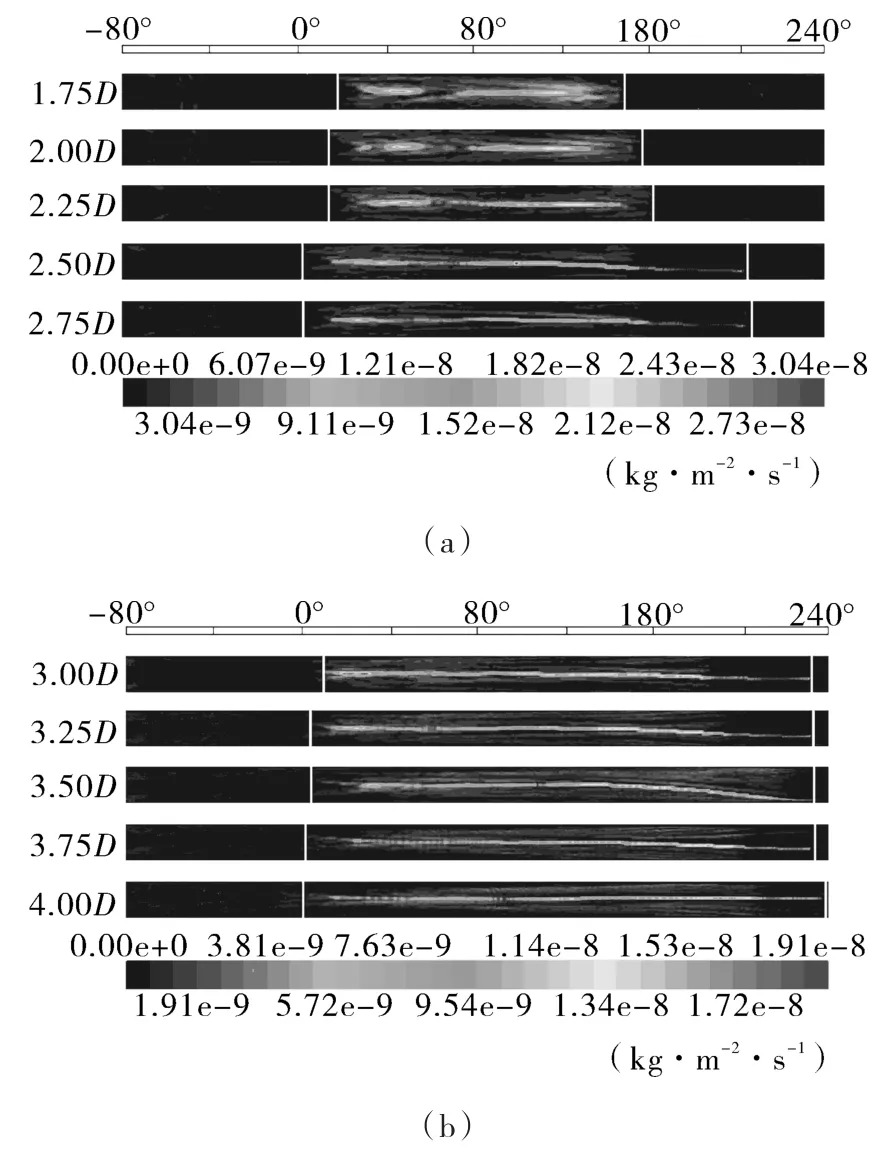
图8 不同弯径比的Ⅳ型补偿器外伸段磨蚀速率Fig.8 The abrasion rate of the extension section of type IV compensator with different bending diameter ratios

在4种标准方形补偿器热补偿量均为100 mm条件下，弯径比为2.75的Ⅰ型补偿器的最大冲蚀速率最低，弯径比为1.5的Ⅳ型补偿器最大冲蚀速率最高，各型补偿器随弯径比增加均出现不同程度的磨蚀现象，以Ⅳ型补偿器最为严重，主要由于Ⅳ型补偿器无外伸水平管的结构使近壁面固体颗粒可以在半圆形管壁的低阻力区滑动，在连续相的携带作用及自身离心作用下［26］，固体颗粒表现出对壁面的“相对黏性”扩大了磨蚀范围。

4 结论

（1）固体颗粒质量流率的增加将增大方形补偿器内的冲蚀速率。其中Ⅰ型补偿器的冲蚀速率与质量流率呈线性正相关，拟合优度超过0.99；Ⅳ型补偿器内冲蚀速率明显高于其它3种补偿器，最大达到 1×10-7kg/（m2·s）量级。

（2）固体颗粒粒径的增加使得各型补偿器先后出现波动幅度在 0～2×10-8kg/（m2·s）范围内的冲蚀速率变化周期，且冲蚀周期内存在明显冲蚀速率“拐点”。Ⅱ型、Ⅳ型与Ⅰ型、Ⅲ补偿器的“拐点”分别出现在粒径为0.5，0.6 mm条件下。

（3）补偿器弯径比的增加会减小固体颗粒对壁面的冲击角度并扩大磨蚀范围。其中，以Ⅳ型补偿器的“带状”磨蚀区域最为显著，弯径比的增加使得其外弧面磨蚀范围由0°～160°扩大至0° ～240°。