弧面凸轮行星减速机构内外弧面凸轮包角的分析与优化

张艳华, 曹巨江, 刘言松, 龚 琰

(陕西科技大学 机电工程学院， 陕西 西安 710021)

0 引言

弧面凸轮行星减速机构在很多文献中亦被称为超环面行星蜗杆传动机构.弧面凸轮行星减速机构具有体积小、传动效率高和承载能力大的优点，在车辆、军事、以及航天领域具有潜在的应用前景[1].该机构主要由外弧面凸轮、内弧面凸轮、行星轮和行星架四个部分组成，如图1所示.外弧面凸轮形似中心蜗杆，与行星轮外啮合，是原动件.内弧面凸轮与行星轮内啮合.行星轮与内、外弧面凸轮同时啮合，是机构动力的传输构件，多个行星轮绕外弧面凸轮轴线均匀分布，每个行星轮上有多个绕行星轮中心均匀分布的滚动齿，滚动齿的形状一般采用滚珠齿、滚柱齿和滚锥齿.旋转运动由外弧面凸轮输入，带动固联于行星架上的行星轮转动，在内弧面凸轮固定的情况下，通过内弧面凸轮上的螺旋槽和行星轮上滚动齿的啮合带动行星架旋转，从而实现运动的输出.

a:外弧面凸轮; b:内弧面凸轮; c:行星轮; d:行星架图1 弧面凸轮行星减速机构

国内外学者对其啮合原理、加工制造和承载能力方面进行了大量的研究.Kuehnle等[2,3]从1980年开始逐渐完成了该传动形式的结构设计、载荷分布计算及定子点蚀等方面的研究成果.Xu L Z等[4,5]对该传动的啮合理论、载荷及应力分布、摩擦润滑、参数优化及结构改进后的机电集成式超环面传动等方面进行了深入的研究.此外，姚立纲等[6-8]、Wei G等[9]、张春丽等[10]、Yang S P等[11]、刘蓓蓓等[12]还从传动效率、结构改进及优化设计、关键零部件的加工方法及建模方法等方面做了不同程度的研究工作.然而，目前研究工作中少有涉及该传动有关外弧面凸轮包容行星轮的角度(简称外弧面凸轮包角，记为α1，如图2所示)和内弧面凸轮包容行星轮角度(简称内弧面凸轮包角，记为α2，如图3所示)问题的研究.这使得在设计弧面凸轮行星减速机构时，内、外弧面凸轮包角两个重要参数的选择上具有一定的盲目性.

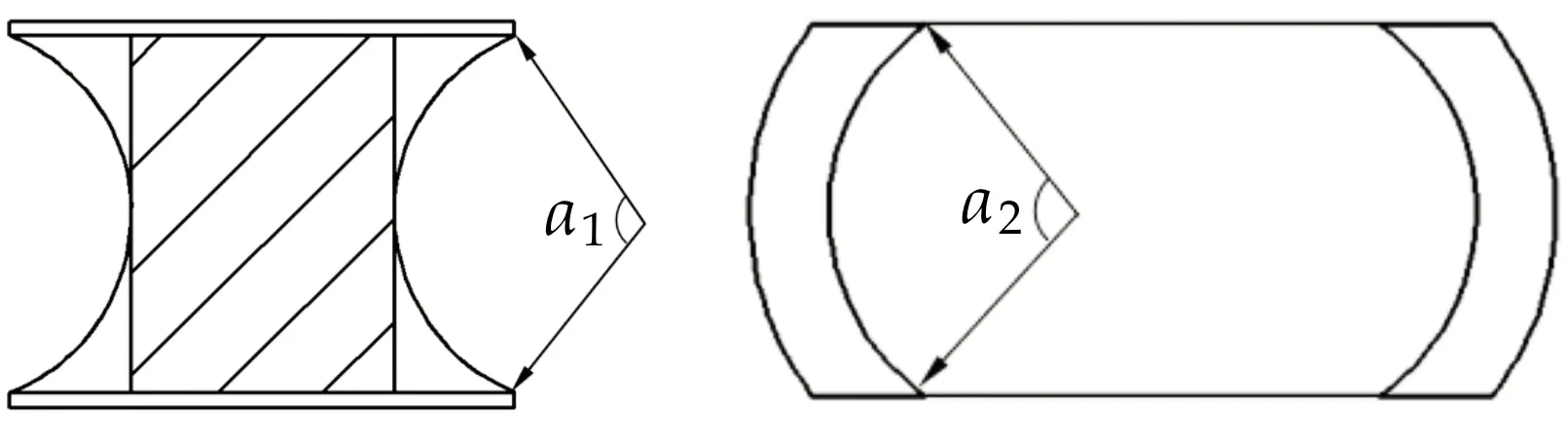
图2 外弧面凸轮包角 图3 内弧面凸轮包角

根据已公开发表文献的不完全统计，所涉及的内、外弧面凸轮的基本参数中，内、外弧面凸轮包角取值多在80 °～140 °之间.弧面凸轮行星减速机构的传动性能与行星轮上同时参与的啮合点的数目有关，而行星轮上同时参与的啮合齿数不仅与行星轮的个数和每个行星轮上滚动齿的个数有关，还与同时啮合的内、外弧面凸轮的包角有关.该传动机构的啮合原理本质上为弧面凸轮机构的啮合原理，所以本文从弧面凸轮的角度进行研究.本文在国内外学者工作的基础上，进一步探索该机构的传动原理，分析了在保证传动连续的情况下，行星轮个数及每个行星轮上滚动齿的个数与内、外弧面凸轮包角间的关系，并通过案例仿真进行了验证，为后续该传动机构的优化设计提供了理论依据.

1 传动分析

为方便分析，对于弧面凸轮行星减速机构引入如下参数及表示符号如表1所示.

表1 参数符号表

由文献[13]可知弧面凸轮行星减速机构相关参数间的关系.

1.1 传动比

内弧面凸轮固定，外弧面凸轮作为输入构件，行星架作为输出构件，则其传动比为：

(1)

式(1)中：±-内、外弧面凸轮螺旋线方向相同时取正，反之取负.

1.2 正确啮合条件

图4为外弧面凸轮以喉部计算圆直径为直径的圆柱体展开图；图5为内弧面凸轮以喉部计算圆直径为直径的圆柱体展开图.

图4 外弧面凸轮展开图 图5 内弧面凸轮展开图

弧面凸轮行星机减速机构的正确啮合条件方程为：

(2)

1.3 装配条件

在设定的机构参数中，除了保证安装行星轮的轴孔在机加工中刀杆不干涉的情况下，行星轮的个数和内外弧面凸轮的齿数需要满足装配条件,装配关系如图6所示.

图6 装配关系图

(3)

式(3)中：N-正整数；

m>0表示内、外弧面凸轮的螺旋线方向相同；反之m<0表示内、外弧面凸轮的螺旋线方向相反.

在设计弧面凸轮行星减速机构时，所需基本参数的给定中，均未涉及外弧面凸轮包角α1和内弧面凸轮包角α2这两个基本参数的选取原则和依据.本文在上述已有关系中，推导了保证传动连续的外弧面凸轮包角α1和内弧面凸轮包角α2的最小值，并在此基础上优化了内、外弧面凸轮包角的取值.

2 内、外弧面凸轮包角与传动连续间的关系

2.1 相邻两行星轮轮齿的相位差

m个行星轮绕外弧面凸轮中心轴线均匀分布，每个行星轮上有均布的z个滚动齿，则第i个行星轮和第i+1个行星轮同一齿的相位差为(其中，i=1,2,3,…，i+1≤m)：

行星轮与外弧面凸轮的传动比为：

(4)

则有：

(5)

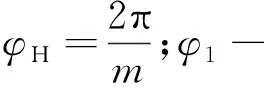
(6)

φH-行星轮上的同一滚动齿相对行星架转过的角度.

联立式(4)～(6)整理可得：

(7)

联立装配条件(2)可得：

(8)

根据上述条件，因为追求大的传动比，一般情况下z1=1，若要满足上述相位角的关系和N取整数的要求，则势必有

以m=3，z=8的行星轮为例，如图7所示，则行星轮沿周向叠加后，其上滚动齿的分布规律如图8所示.

图7 行星轮示意图

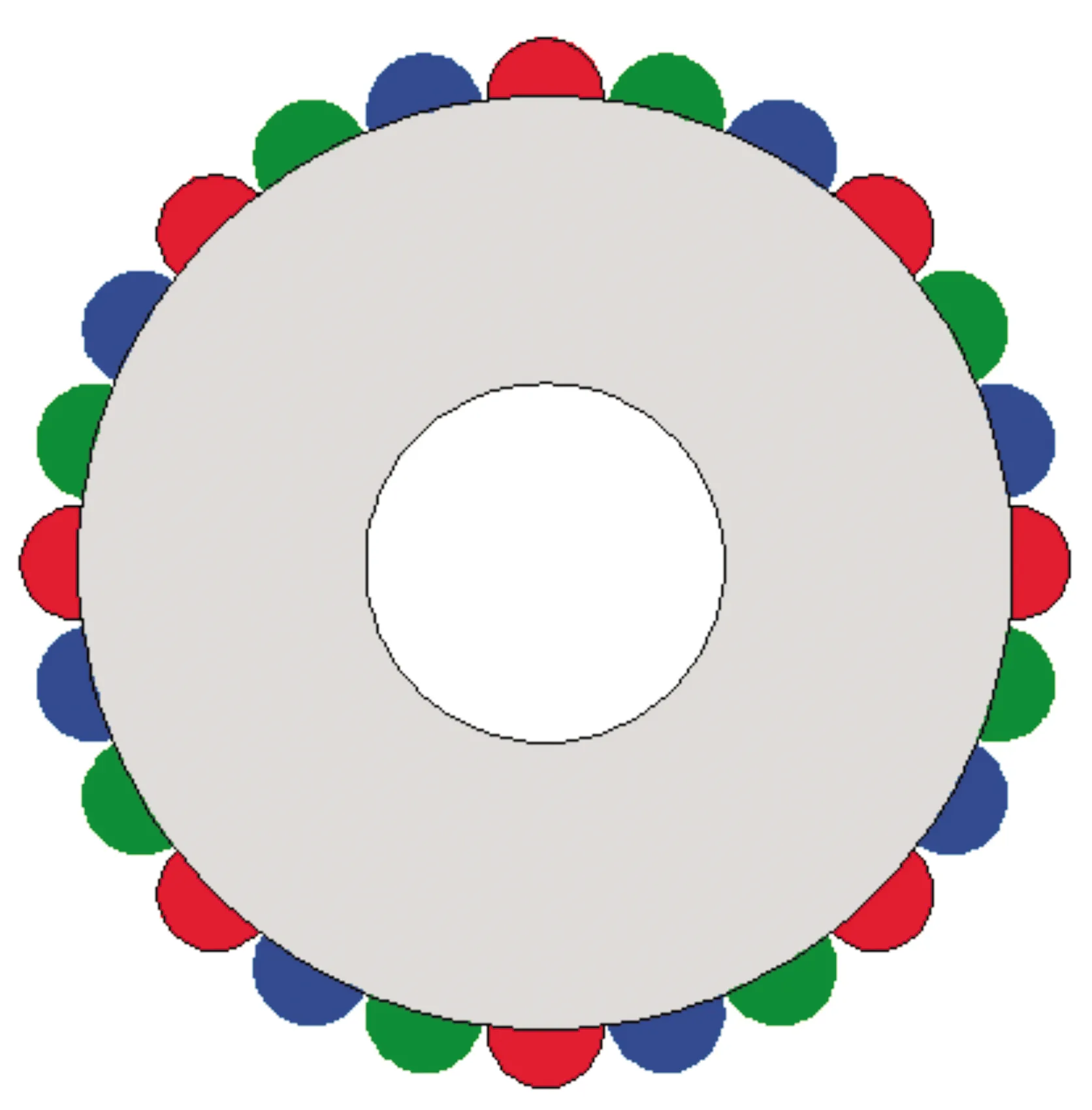
图8 滚动齿分布规律图(绿色代表轮1；红色代表轮2；蓝色代表轮3)

2.2 连续传动条件

要使弧面凸轮行星减速机构运动连续，则内弧面凸轮与i个行星轮的每个轮上至少有1个滚动齿啮合接触，同时外弧面凸轮至少与其余(m-i)个行星轮的每个轮上至少有1个滚动齿啮合.

2.3 α1和α2的最小值

为满足上述条件，行星轮上滚动齿的个数最小取2，即z为正整数，且z≥2.行星轮的个数m为正整数.

(1)当m=1， 该情况较为特殊，这时唯一的行星轮上需要有滚动齿同时与内、外弧面凸轮啮合，所以此时蜗杆包角α1和超环面包角α2关系有：

(9)

该种情况理论上分析存在，但实际结构中由于只存在一个行星轮，将导致偏载现象严重，所以实际设计中不便于采用.

(2)当m=2时，这时同一个星轮上必有一个滚动齿，要么与外弧面凸轮啮合，要么与内弧面凸轮啮合，位于行星轮两侧的内、外弧面凸轮其包角关系有：

(10)

此时，若内、外弧面凸轮包角均取最小值，则该传动机构中，共有2个点参与啮合，即一个行星轮上的一个滚动齿与外弧面图轮啮合，另一个行星轮上的滚动齿恰与内弧面凸轮啮合.换言之，若想传动连续，所有行星轮上至少有2个点参与啮合，一个点与内弧面凸轮啮合，一个点与外弧面凸轮啮合.

(3)当m≥3时，内、外弧面凸轮包角关系同上述(2)中关系，即：

(11)

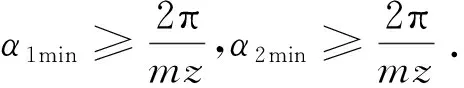
由上述分析可见，在行星轮上滚动齿个数z不变的情况下，内、外弧面凸轮包角之和的最小值将不发生改变，在包角之和最小值不变的情况下，当行星轮个数增加，啮合过程中将会有多余的啮合点(主要起均布载荷的作用).在内、外弧面凸轮包角均取最小值的情况下，冗余啮合齿数为m-2.

3 内、外弧面凸轮包角的优化

弧面凸轮行星减速机构作为一种高效能的空间啮合传动机构，所以在运行过程中，应尽可能的增加参与的啮合齿数.弧面凸轮行星减速机构运行过程中，外弧面凸轮、内弧面凸轮和多个行星轮上的滚动齿共同参与啮合，参与啮合的齿数随着行星轮转角和内、外弧面凸轮包角的改变而改变，所以考虑到运行过程中传递动力的稳定性，应保持啮合状态的滚动齿的总对数恒定.在其它参数确定的情况下，增大内、外弧面凸轮的包角可以增加参与啮合的行星轮滚动齿数，从而增加啮合齿数.若内、外弧面凸轮包角恰好是内、外弧面包角最小值的整数倍时，在该机构运行过程中，当一个行星轮上的滚动齿脱离内、外弧面凸轮包角时，后续行星轮的滚动齿恰好进入内、外弧面凸轮的包角内参与啮合，所以，整个运行过程中，参与啮合的行星轮滚动齿总对数既不增加，也不减少，保持恒定.即，外弧面凸轮包角和内弧面凸轮包角在保证上述条件的情况下，还应该满足：

(12)

(13)

式(13)中：n为正整数.

4 验证分析

针对上述分析，根据空间啮合及装配关系，选取弧面凸轮行星减速机构的结构参数，并对其进行仿真计算分析.基本结构参数如表2所示.

表2 基本结构参数表

按照外、内弧面凸轮包角与传动连续间的关系可知，此时外、内两弧面凸轮的包角的最小值为：

(α1+α2)min=60 °

且α1min≥12 °,α2min≥12 °

按上述分析，在满足内、外弧面凸轮包角最小取值的条件下，考虑到机构传动的平稳性和高效性，内、外弧面凸轮包角可取120 °、108 °、96 °和84 °.在内、外弧面凸轮不同包角的情况下，啮合点总数随行星轮位置角度的变化规律如图9所示.

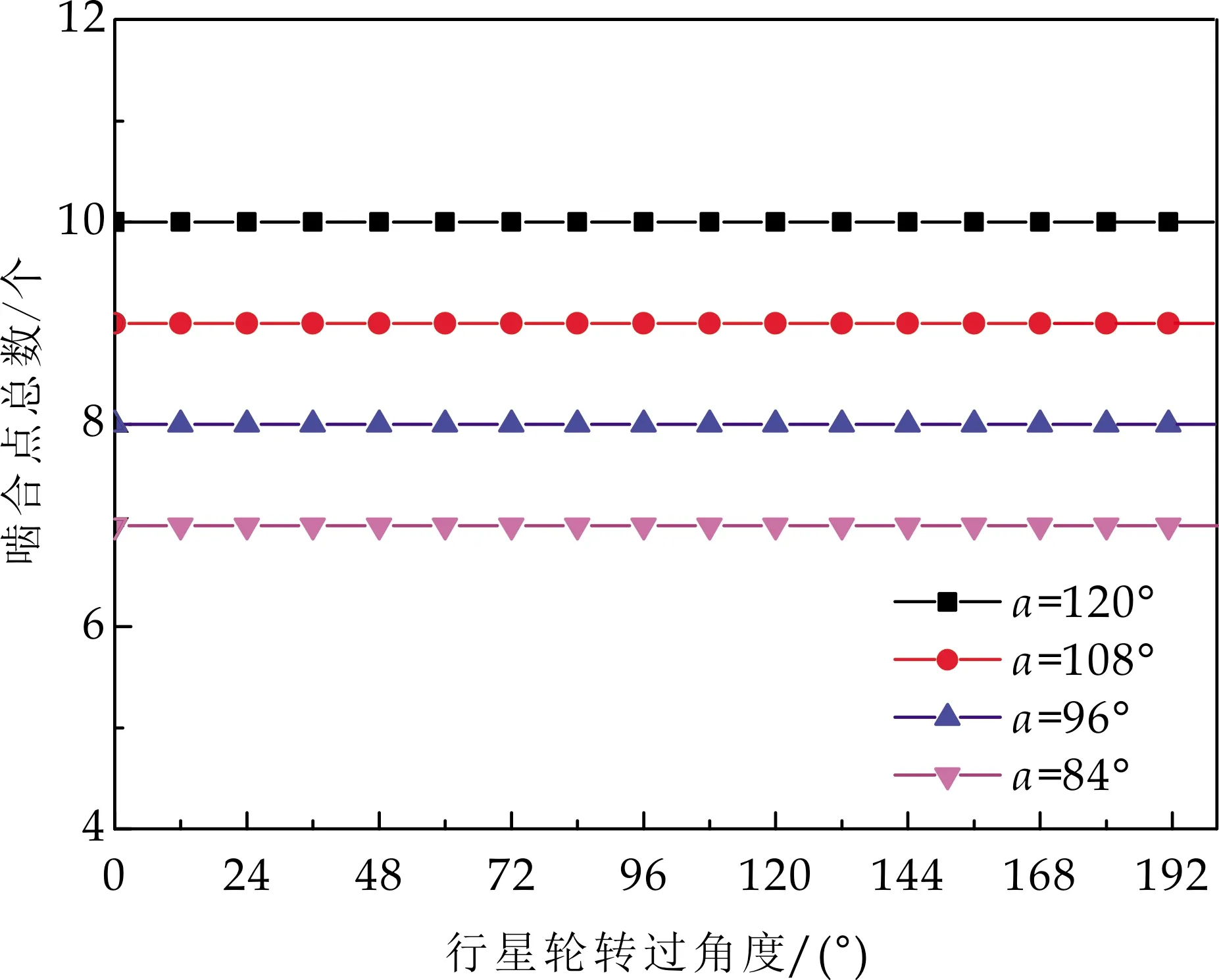
(a)外弧面凸轮上啮合点总数变化规律

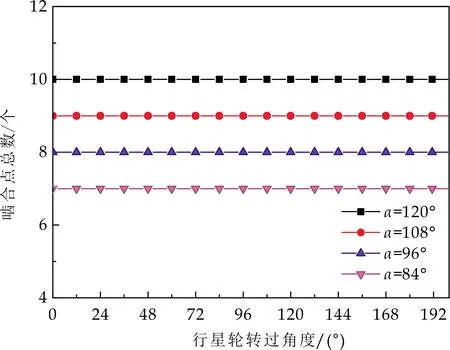
(b)内弧面凸轮上啮合点总数变化规律图9 啮合点总数随行星轮位置角度的变化规律

由图9可以看出，在行星轮齿数一定的情况下，随着内、外弧面凸轮包角的不同，行星轮分别于内、外弧面凸轮的啮合总齿数也不相同，啮合总齿数随内、外弧面凸轮包角的增大而增加.在内、外弧面凸轮包角合理的取值下，行星轮与内、外弧面凸轮的啮合总齿数始终为整数，并且啮合总齿数个数的多少可以通过包角的大小进行控制.

随着内、外弧面凸轮包角的不同，单个行星轮参与啮合的齿数各不相同，以单个行星轮来看，每半个运动周期中，参与啮合齿数的变化规律如图10所示.

(a)内、外弧面凸轮包角为120 °时

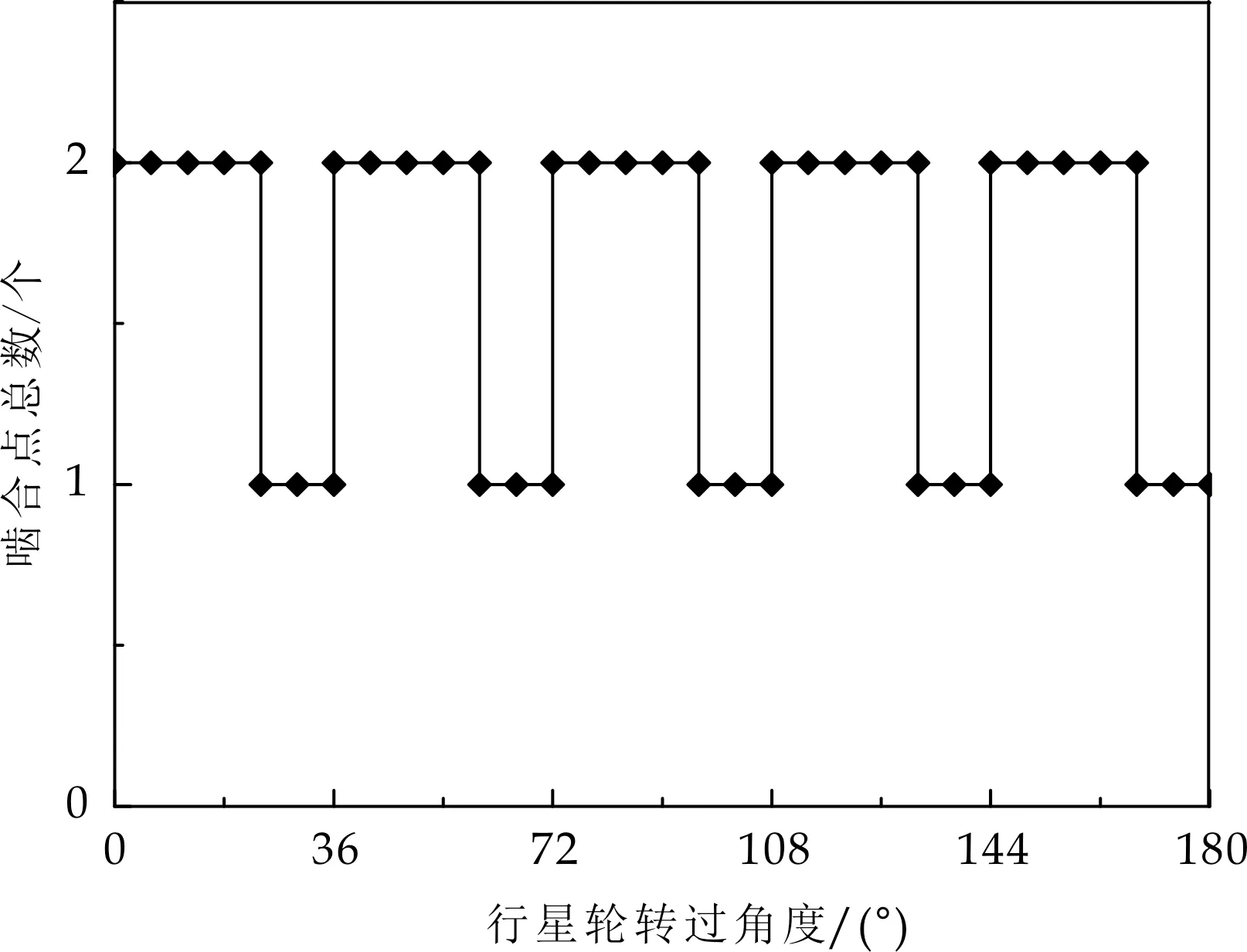
(b)内、外弧面凸轮包角为108 °时

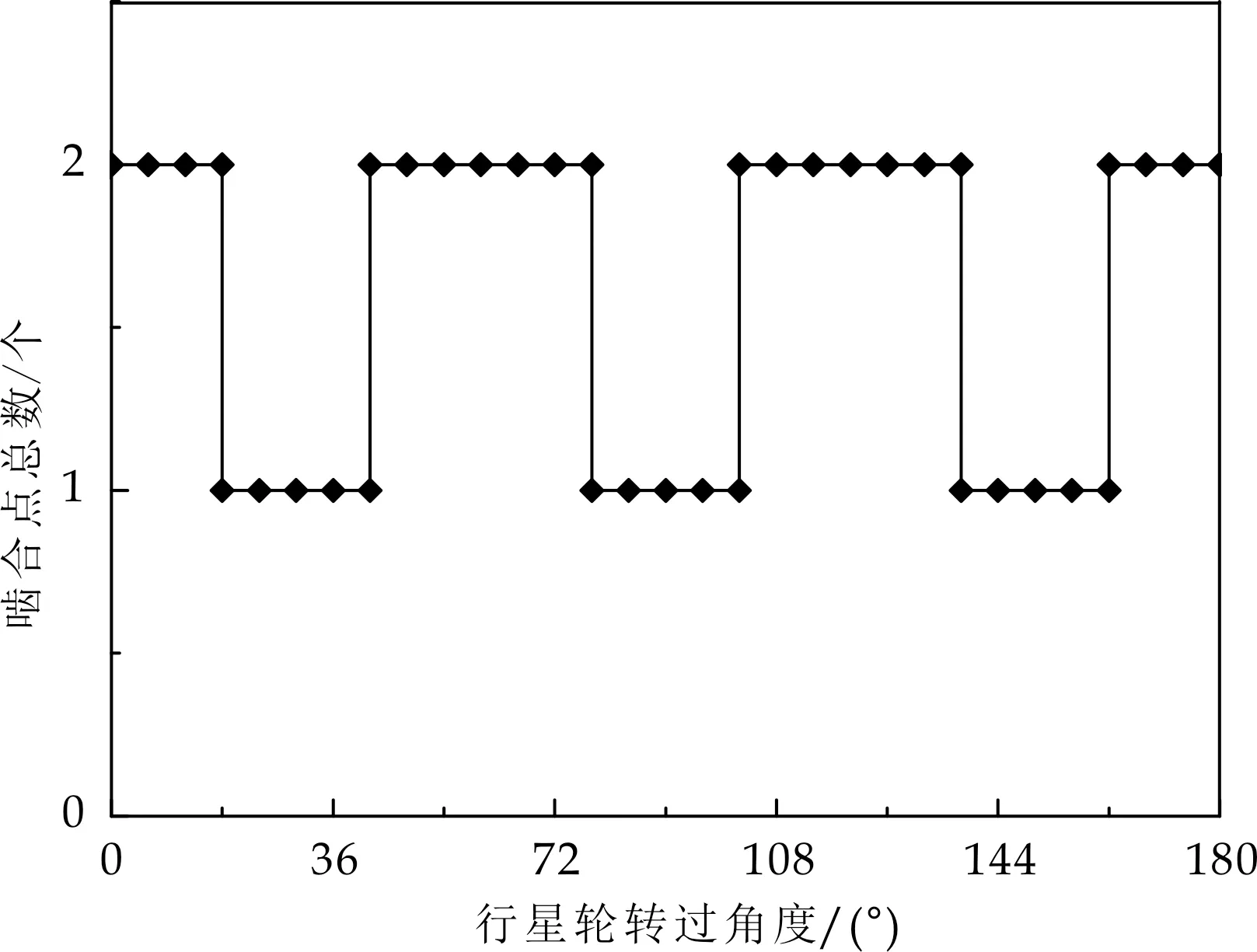
(c)内、外弧面凸轮包角为96 °时

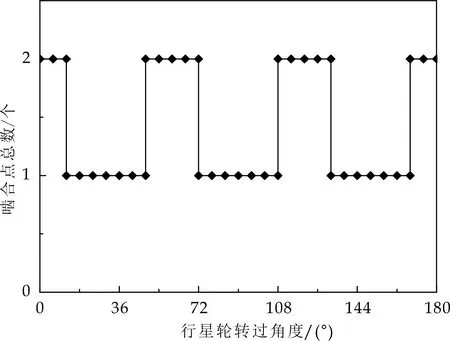
(d)内、外弧面凸轮包角为84 °时图10 不同包角下啮合点的变化规律

由图10可得，当行星轮齿数一定，而内、外弧面凸轮包角的不同时，所有行星轮参与啮合的总齿数不变，但是就单个行星轮而言，参与啮合的齿数随内、外弧面凸轮包角的增加而增多，并且，在啮合齿数相同的情况下，随包角的增大，参与多点啮合的时间增长.

由图9和图10综合可得，兼顾单个行星轮参与啮合的周期数和所有行星轮参与啮合的滚动齿总数，内、外弧面凸轮包角均取120 °为佳.此时，不仅内、外弧面与所有行星轮啮合的总齿数恒定，并且就单个行星轮而言，参与啮合的齿数也为定值，这就使得弧面凸轮行星减速机构运行过程中，不存在多齿和少齿的变化，能有效减小输出动力的波动性.

5 结论

本文针对弧面凸轮行星减速机构传动特性进行分析，在保证运动连续的情况下，通过对内外弧面凸轮包角的计算分析和仿真结果，得到了如下结论：

(1)当行星轮上滚动齿的个数z一定时，内、外弧面凸轮包角之和的最小值为定值，不会因为行星轮的个数m的增加而减小.但是，内、外弧面凸轮包角的可以取的最小值会随行星轮个数m的增加而减小.

(2)当在内、外弧面凸轮包角取值最小时，传动过程中的啮合齿数最小为2，随着行星轮个数的增加，多余啮合齿数为m-2.

综上所述，在设计行星轮系弧面凸轮传动机构时，除应充分考虑其传动比、啮合条件和安装条件外，为保证动力传递的连续性和稳定性，还应兼顾考虑内、外弧面凸轮包角和行星轮个数及每个行星轮上滚动齿的个数间的关系.上述结论为后续弧面凸轮行星减速机构的优化设计提供了理论依据.