带交换和跳跃的一维双向自驱动系统的仿真研究

费大智，郝庆一

（安庆师范大学数理学院，安徽安庆246133）

自驱动粒子系统是研究非平衡态系统的一类简单而又富有代表性的模型。这类模型的常用形式就是非对称排他过程（Asymmetric Simple Exclusion Processes,ASEP），ASEP模型最早由两位以色列数理生物学家麦克唐纳和吉布斯于1968年提出，并用于模拟生物高聚合动力学[1]；之后被很多学者进行了扩展和延伸，应用于蛋白质合成、分子马达、行人、车辆交通等运输系统的研究中[2-4]。

本文考虑一维ASEP模型，在这个自驱动系统中，有两种粒子，一种粒子向右移动，另一种粒子向左移动，两种粒子相遇时，可以换位，而且后面的粒子可以跳过前方粒子。这种换位行为在行人流中经常遇到，跳跃行为在行人和车辆交通中也可理解为绕行超越或换道超车。在分子马达实验观测中有学者发现有的分子马达在遇到障碍物时，也会发生类似的跳跃行为以越过障碍物。

1 模型

在总长度为L的一维格链上，随机分布着密度分别为ρ1和ρ2的右向行驶粒子和左向行驶粒子。在第一个子时间步，随机选择一个格点i（1≤i≤L），按照下列规则更新位置（规则示意图如图1所示）：

（Ⅰ）若i格点为空，则该格点保持不动。

（Ⅱ）若i格点被右行粒子占据，则按下列规则更新：

①i+1格点为空，粒子跳入i+1格点；

②i+1格点被左行粒子占据，左行粒子和右行粒子以概率k交换；

③i+1格点被粒子占据，i+2格点为空，且i格点粒子未与i+1格点粒子发生交换，粒子以概率r1跳至i+2格点。

（III）若i格点被左行粒子占据，按下列规则更新：

①i-1格点为空，粒子跳入i-1格点；

②若i-1格点被右行粒子占据，则左行粒子和右行粒子以概率k交换；

③若i-1格点被粒子占据，i-2格点为空，且i格点粒子未与i-1格点粒子发生交换，粒子以概率r2跳至i-2格点。

（IV）每个子时间步随机选取一个格点按以上规则更新，L个子时间步更新合成为一个完整的时间步更新，系统采用周期性边界。

图1 模型更新规则示意图

2 模拟与分析

这里分别给出改变左右粒子密度比、跳跃概率、交换概率的计算机模拟结果。在模拟中，取L=200，时间步T取20 000～100 000。为了便于分析研究，在本模型中左右双向运动的粒子跳跃概率和交换概率都相同。

2.1 不同密度比

图2为跳跃概率r=0.9，交换概率k=0.5，左右粒子密度比例ρ1：ρ2分别为1∶9、2∶8、3∶7、4∶6、5∶5下的系统密度-流率图。可以看出左右粒子数量越接近，如ρ1∶ρ2为3∶7、4∶6、5∶5时，系统流率就越大。这是因为两种粒子的数量相对接近时，粒子之间发生交换和跳跃的几率变大，从而导致系统流率增大。左右粒子数量差距较大时，如ρ1∶ρ2为1∶9、2∶8，随着系统粒子密度的增大，系统流率在高密度处反而降低。此时由于粒子数量差距较大，系统密度增大，系统中会出现数量大的同向粒子彼此相连，此时跳跃规则和交换规则对系统流率的影响较小，系统发生堵塞，从而导致系统流率降低。

2.2 不同跳跃概率

图3和图4为粒子密度比率ρ1∶ρ2=1∶1，跳跃概率r分别为0.1、0.3、0.5、0.7、0.9时的系统密度-流率图，图3中粒子的交换概率k=0.5，图4中粒子的交换概率k=0.6。可以看出系统流率随着系统密度的增大而增大，但图像只在系统处于中段密度区（0.3＜ρ＜0.8）时有分离，在低密度区（ρ≤0.3）和高密度区（ρ≥0.8）不同交换概率k下的图像趋于重合。下面分析这种情况出现的原因。

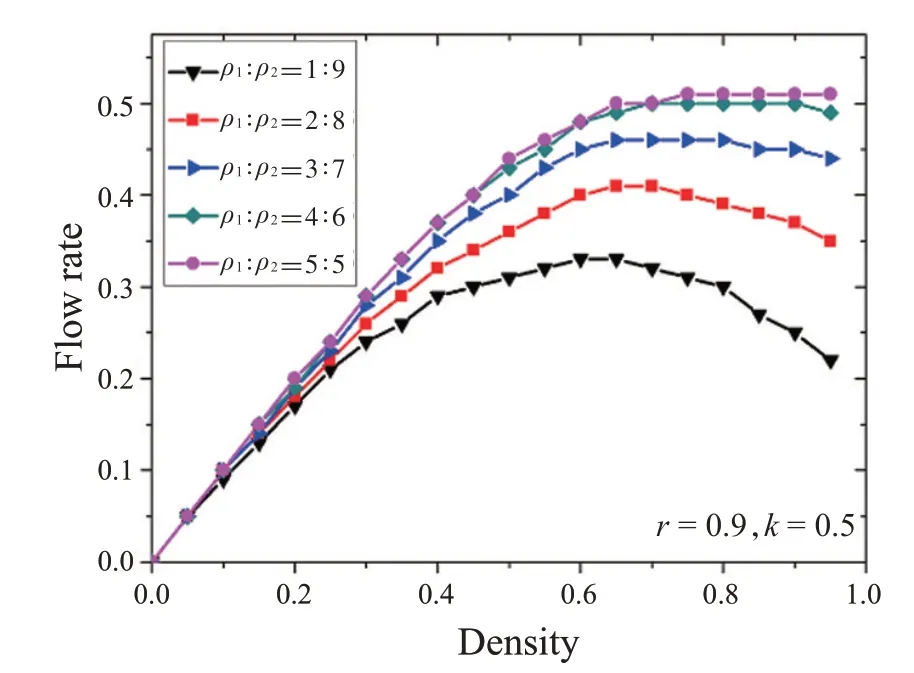
图2 不同粒子比率下的流率-密度图

图3 不同跳跃概率下的流率-密度图

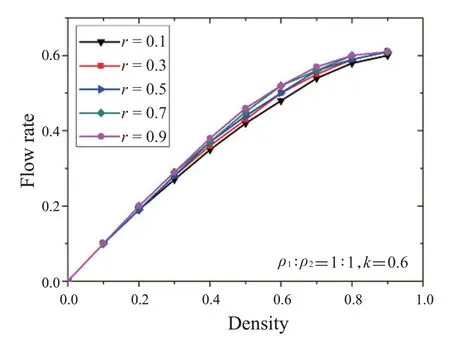
图4 不同跳跃概率下的流率-密度图

系统处于低密度区时，粒子数较少且系统采取随机更新，系统选取到空格概率较高，两粒子相邻的概率较低，这些都导致跳跃规则失效，因此在低密度区不同跳跃概率下的系统流率区分不明显；

系统处于中段密度区时，增大粒子跳跃概率可以让系统流率增大，此时粒子数较低密度区更多，且系统有充足的空格让粒子跳跃，跳跃概率增大，系统流率增大；

系统处于高密度区时，粒子数最多，但空格较少，这导致粒子无法跳跃，因此在高密度区不同跳跃概率下的系统流率区分不明显。

2.3 不同交换概率

图5为左右粒子密度比ρ1∶ρ2=1∶1，左右粒子跳跃概率r=0.1，交换概率k分别为0.1、0.3、0.5、0.7、0.9时的系统密度-流率图。可见，随着k的增大，系统流率增大，增速变快，流率峰值处于系统最大密度处。

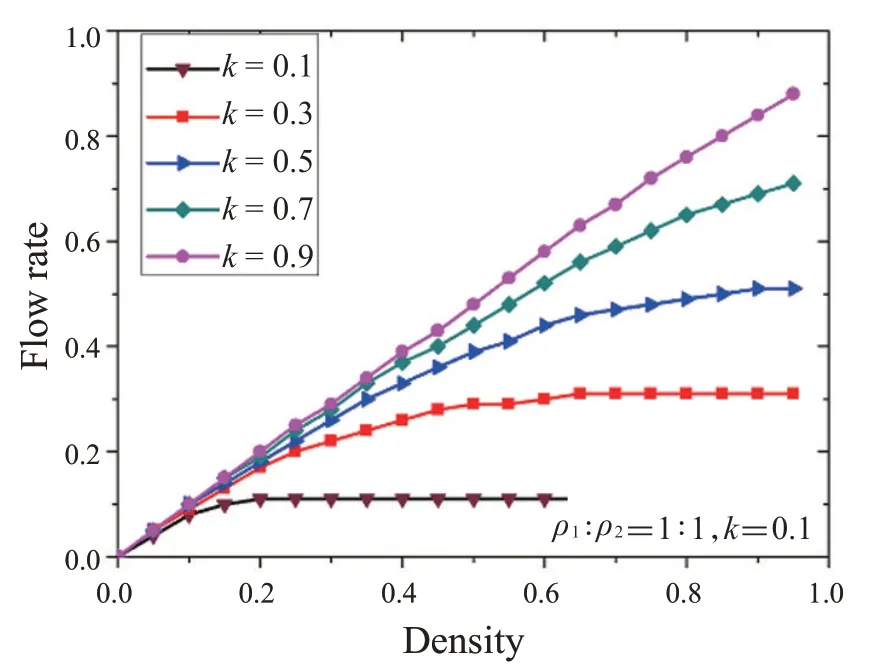
图5 不同交换概率下的流率-密度图

2.4 系统回滞现象

下面探讨该系统是否存在回滞现象[5-6]。为此，采用从低密度开始逐步增加系统密度和从高密度开始逐步减少系统密度两种方式计算系统流率。在相同参数条件下，得到两条流率-密度曲线。这里取L=200，时间步T取20 000～100 000。

图6～9是不同参数下的系统流率-密度图。可以看出，相同参数下两条曲线几乎重合，没有形成回滞环，由此可知该系统没有出现回滞现象。

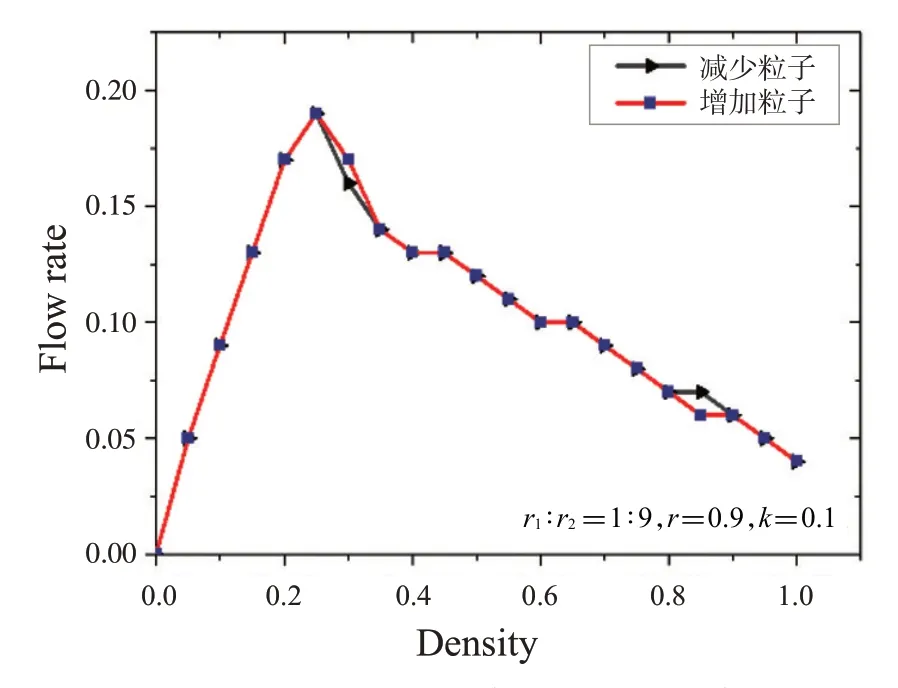
图6 左右粒子比率1∶9，跳跃概率0.9，交换概率0.1下的流率-密度图

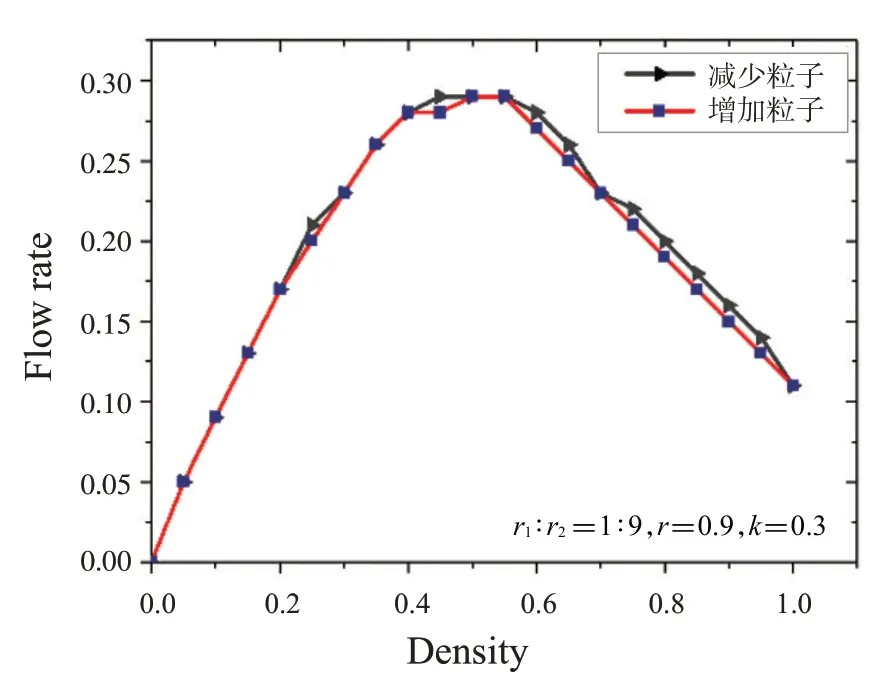
图7 左右粒子比率1∶9，跳跃概率0.9，交换概率0.3下的流率-密度图

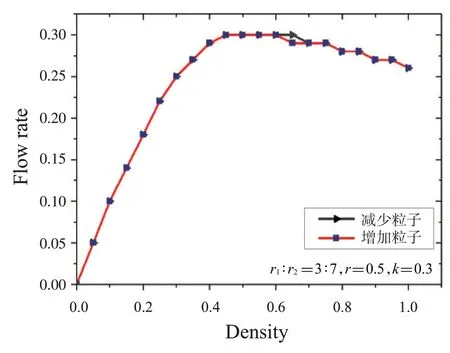
图8 左右粒子例3∶7，跳跃概率0.5，交换概率0.5下的流率-密度图

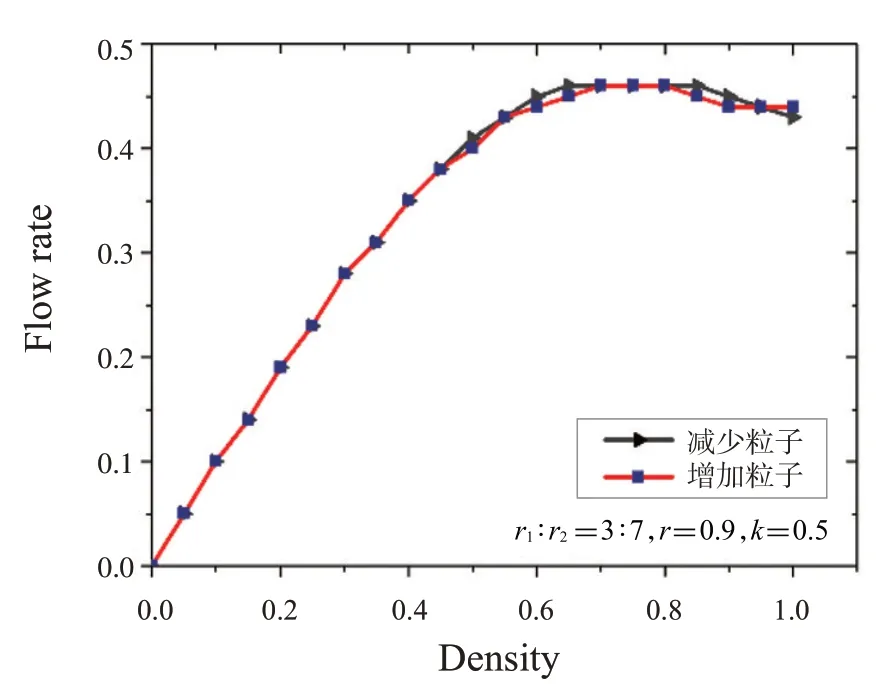
图9 左右粒子比例3∶7，跳跃概率0.9，交换概率0.5下的流率-密度图

3 结论

综合上述结果，我们得出以下结论：①两种粒子的比例越接近，系统流率越大；②在密度位于中段区域时（0.3＜ρ＜0.8），粒子跳跃概率越高，系统流率就越大；③对向粒子交换概率越大，系统流率就越大，流率-密度曲线由非单调转变为单调递增；④该系统没有出现回滞现象。这些结论对行人、车辆交通等自驱动系统的理解是有帮助的，也将有助于对非平衡态系统性质的理解。